变异系数

#一日一词#

前一周找工作去了，整天累成狗  凸(艹皿艹 )，所以也没能做到一日一更，后续慢慢补上。( ｀д′)

结合之前的《标准差》

方差和标准差是用来反映一组数值变异程度的绝对值，其大小受到样本的值大小、计量单位等的影响，因此不能用于不同水平、不同计量单位的样本比较，即是说，针对来自不同总体的样本，不能直接计算方差或标准差进行比较。

这里就引出了变异系数，也叫离散系数、标准差系数或差异系数，是样本数据的标准差与其平均值之比，用CV表示。公式：

​CV=标准差/算术平均值

通常用于比较几个量纲不同的变量之间的离散程度。

（提示一些，在这里，“样本来自不同整体”和“样本量纲不同”想表达的是一个意思，就是说样本在不同组，因为不同组的平均值、样本大小等可能不同，所以不能直接比较离散程度）

举个栗子：

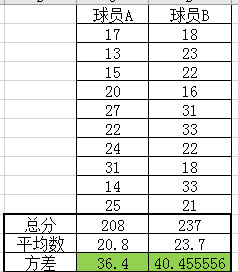
比较一下两个球员的成绩（每场比赛得分总数），判断球队选择哪一个稳定成绩些？

看上去A球员虽然平均分虽然删了3分，但相比下要稳定些。（补充：在Excel中，计算样本方差的函数是VAR，标准差函数是STDEV）

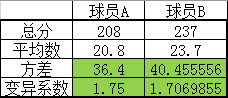
然而如果比较变异系数：

​结果的确球员B要好些，不仅总分数和平均分数高，还相对稳定。（数据是我捏造的，可能不太合适，不过重要的是思想。）

转载于:https://www.cnblogs.com/rhongp/p/6383849.html