二阶行列式的几何意义
二阶行列式 \(D = \begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a_1b_2 - a_2b_1\) 的几何意义是以向量 \(\vec a = (a_1, a_2), \vec b = (b_1, b_2)\) 为邻边的平行四边形的有向面积。
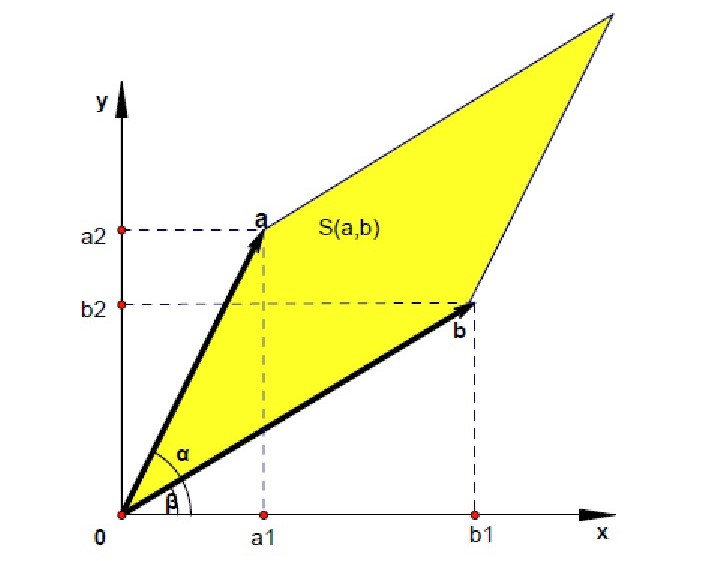
根据以上条件,知四边形的面积 \(S(\vec a, \vec b) = ab \sin{<\vec a, \vec b>}\)
其中,\(a = \sqrt{a_1^2 + a_2^2}\) , \(b = \sqrt{b_1^2 + b_2^2}\) ,
\(\sin{<\vec a, \vec b>} = \sin{(\alpha - \beta)} = \sin{\alpha}\cos{\beta} - \cos{\alpha}\sin{\beta} = \frac{b_2}{b} \frac{a_1}{a} - \frac{b_1}{b} \frac{a_2}{b} = \frac{a_1b_2 - a_2b_1}{ab}\)
整理,得 \(ab \sin{<\vec a, \vec b>} = a_1b_2 - a_2b_1\)
而 \(\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a_1b_2 - a_2b_1\)
所以
\[
\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = S(\vec a, \vec b)
\]
三阶行列式的几何意义
三行列式是其行向量或列向量所张成的平行六面体的有向体积。
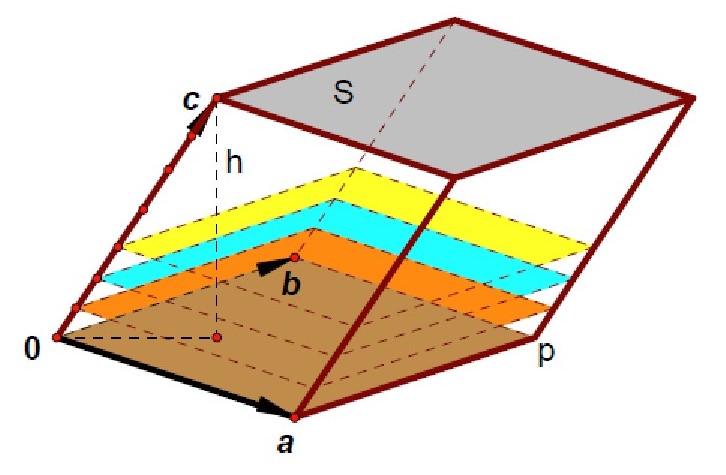







 本文深入探讨了二阶和三阶行列式的几何意义,揭示了它们分别代表的平行四边形有向面积和平行六面体有向体积的数学原理。通过向量和角度的分析,阐述了行列式在计算图形面积和体积中的应用。
本文深入探讨了二阶和三阶行列式的几何意义,揭示了它们分别代表的平行四边形有向面积和平行六面体有向体积的数学原理。通过向量和角度的分析,阐述了行列式在计算图形面积和体积中的应用。
















 781
781

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








