[CSP-S模拟测试]:虎（DFS+贪心）

题目传送门（内部题15）

---

输入格式

第一行一个整数$n$，代表点数
接下来$n-1$行，每行三个数$x,y,z$，代表点$i$与$x$之间有一条边，若$y$为$0$代表初始为白色，否则为黑色，若$z$为$0$代表不对最终颜色做要求，否则代表要求为黑色。

---

输出格式

达到目的的最少操作多少次数。

---

样例

样例输入：

7
1 0 1
1 1 1
2 0 1
2 0 1
3 1 1
3 0 1

样例输出：

3

---

数据范围与提示

对于$30\%$的数据，所有的$x$等于$1$。
对于$70\%$的数据，所有边最终都必须为黑色
对于$100\%$的数据，$n\leqslant 1,000,000$。

---

题解

先看数据范围，$n\leqslant 1,000,000$（注意是一百万，不是十万，可能只有我数不清几个$0$了吧？），这只能允许我们$\Theta(n)$。

$70\%$算法：

还是先从部分分下手，先来考虑$70\%$的数据，所有便最终都必须为黑色，考虑贪心。

比方说有下面这样一条链：

我们可以选择翻转$1\sim 3$和$4\sim 5$，也可以选择先翻转$1\sim 5$再将$3\sim 4$翻转回来，但是都需要两步，所以我们可以贪心的扫每一条链，直到扫到一条黑边为止，把这中间的都翻转即可。

那么现在来考虑许多边连向一个点的情况：

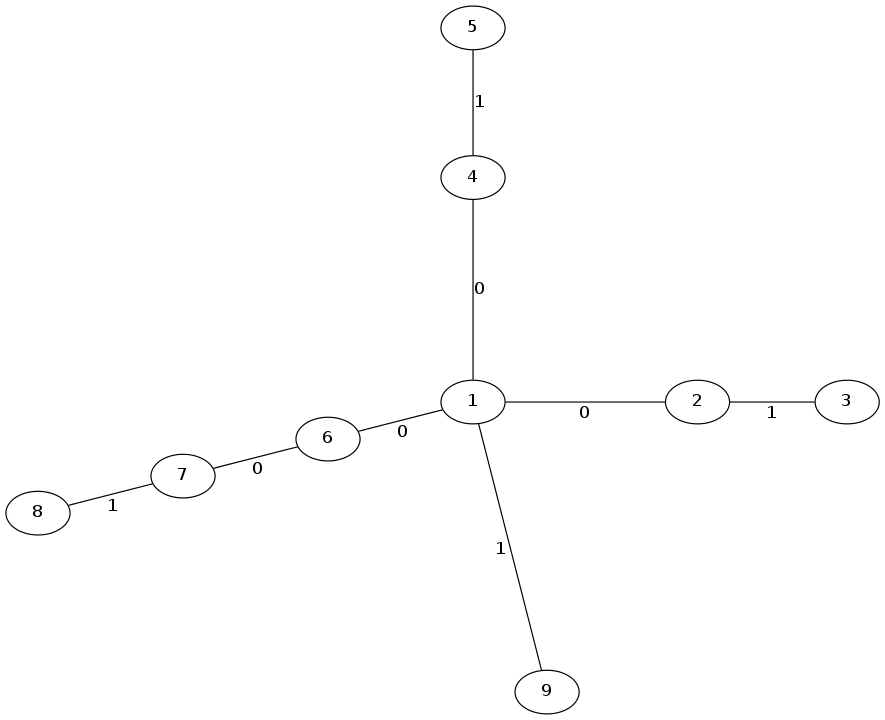
比方说上面这张图，一共有三个白边连向点$1$，你可能首先会下意识的以为需要翻转三次（聪明的你也可能没有），但是仔细一想，我们可以把这其中任意两个翻转合并，如翻转$2\sim 1\sim 4$这条路径，然后再翻转$1\sim 7$这条路径以达到目的。

那么不妨这样讲，对于多条边连向一个点的情况，其所需的翻转次数即为$\left \lceil \frac{黑边个数}{2} \right \rceil$。

时间复杂度：$\Theta(n)$。

期望得分：$70$分。

实际得分：$60$分。

$100\%$算法：

显然对于一道$T1$来说，我们应该$A$掉它。

发现每条边只会被要求为黑色，或者是任意颜色，所以在来贪心。

对于任意颜色，我们可以无视它，这不太好想，但仔细一想也是对的，我也不知道该怎么解释了，自己体会吧？所以我们可以把这种边缩掉，我的方法是用一个类似并查集思想的东西，但是比并查集简单的多。

时间复杂度：$\Theta(n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to,w;}e[2000001];
int head[1000001],cnt=1;
int n;
bool vis[2000001];
int fa[1000001];
int ans;
void add(int x,int y,int w)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	e[cnt].w=w;
	head[x]=cnt;
}
void dfs(int x)
{
	for(int i=head[x];i;i=e[i].nxt)
		if(!vis[i]&&!e[i].w)
		{
			vis[i]=vis[i^1]=1;
			dfs(e[i].to);
			return;
		}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)fa[i]=i;
	for(int i=2;i<=n;i++)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		if(!z)fa[i]=fa[x];
		else
		{
			add(i,fa[x],y);
			add(fa[x],i,y);
		}
	}
	for(int x=1;x<=n;x++)
	{
		int sum=0;
		for(int i=head[x];i;i=e[i].nxt)
			if(!vis[i]&&!e[i].w)
			{
				vis[i]=vis[i^1]=1;
				dfs(e[i].to);
				sum++;
			}
		if(sum&1)ans+=sum/2+1;
		else ans+=sum/2;
	}
	printf("%d",ans);
	return 0;
}

---

rp++

转载于:https://www.cnblogs.com/wzc521/p/11425001.html