DFT的补0运算

在实际的DFT中，如果需要增加采样的密度。这里的采样是频域的采样。可以等到更加密集的谱。

如对于信号 x = [1, 1, 1, 1]做DFT如下图：

不零后的DFT， N = 8, N= 16, N= 32

 

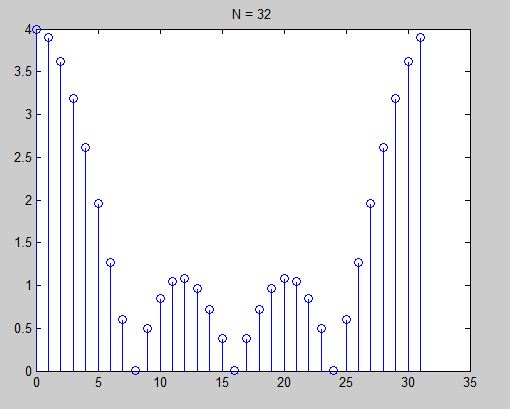
结论：补零就是将原序列后增加0，使原序列增长。使DFT有更高密度的谱，但是没有给出一个更高分辨率的谱。因为没有任何新的信息附加到这个信号上,而仅仅是在数据添加额外的0， 为了要得到更高的分辨率的谱就必须获得更多的有效数。

 

 

为了证明结论：

xn = cos(0.48pi * n) + cos(0.52pi * n), 在n = [0: 10]加90个零的频谱，和直接n= [0:100]的频谱比较。在没有做DFT前，可以知道xn的频谱是两个脉冲。且脉冲的位置在0.48pi和0.52pi。