8 中性集在医学图像聚类中的应用
艾哈迈德·拉法特·哈瓦斯*,阿米拉·S·阿舒尔*,郭艳晖†
*坦塔大学工学院电子与电气通信工程系,埃及坦塔。 †伊利诺伊大学斯普林菲尔德分校计算机科学系,美国伊利诺伊州斯普林菲尔德
1 引言
聚类是一种对数据进行分组的无监督过程。它通过将特征集转换为子集,在没有先验信息的情况下对数据实例进行分组,其中相似的特征被标记为属于同一子集。数据聚类通过发现数据中的相似性,将其分配到同一组中。聚类将数据集划分为若干组,使得组内的相似性大于组间的相似性。聚类的主要目标是基于未标记数据在不同数据簇之间构建边界。它在多维特征空间中寻找分组簇,由于簇的大小和形状各不相同,这一过程具有挑战性(Jain, Duin,& Mao, 2000)。聚类过程可分为划分式和层次式,例如围绕中心点划分(PAM)、K‐均值以及基于EM(期望最大化)算法的高斯混合模型(Revathi& Nalini, 2013)。在PAM聚类方法中,簇内会确定一系列位于中心位置的中心点(即从选定对象集中选出的对象)。这些中心点通过最小化对象与其最近选定对象之间的平均相异度获得(Van der Laan, Pollard,& Bryan, 2003)。在K‐均值聚类中,使用L2范数在收敛时将数据点分配给特定簇,以确定最优簇及其对应的质心(El Agha&Ashour, 2012;Shmmala& Ashour, 2013; Steinley, 2006)。然而,在使用EM算法进行聚类时,保留的是概率分配而非确定性分配,其中多元高斯分布被采用。它使用期望而不是L2范数来计算任意数据点属于任一质心的概率(Basu, Banerjee,& Mooney, 2002;Frey& Jojic, 2003)。通常,主要的聚类算法是K‐均值(硬C均值),用于硬分割(Ghosh& Dubey, 2013)。
在医学应用中,图像包含不精确的信息和模糊性,导致聚类、分割和分类过程更加复杂。因此,在此类应用中可采用模糊聚类来处理不确定性和模糊性,从而将数据点按照不同的隶属度水平分类到多个固有的聚类中(贝兹戴克、霍尔和克拉克,1993)。在硬聚类(非模糊聚类)中,数据被划分为清晰聚类,每个数据点仅属于一个特定的聚类。而在模糊聚类中,数据点可以被分配到多个聚类中,隶属度水平用于表示数据点对不同聚类的归属程度(德、比斯瓦斯和罗伊,2001)。已提出多种基于模糊的聚类方法,包括模糊 C均值(FCM)(陈、吉格和比克,2006;庄、曾、陈、吴和陈,2006)、可能性模糊C均值(帕尔、帕尔、凯勒和贝兹戴克,2005)以及关系证据C均值(RECM)(Masson& Den ux,2009)。然而,模糊聚类方法的主要局限性包括所需的停止准则、易陷入局部极小值而导致非最优解的问题,以及由于噪声和伪影而忽略了像素空间上下文(孔达尔、古普塔和辛格,2012)。为了克服基于模糊方法的局限性,作为模糊集的一种广义形式的中性集(NS)在多个图像处理阶段中变得更为普遍。
基于中性集(NS),已提出多种技术来减少不确定性。郭和 Sengur(2015)结合模糊C均值与NS框架,提出了一种中性c均值(NCM)方法用于不确定数据聚类。该聚类过程被表述为一个约束最小化问题,旨在最小化预定义的目标函数。该目标函数包含模糊拒绝和距离拒绝,分别用于处理靠近聚类边界以及远离所有聚类的模式。中性集(NS)提供了应对聚类不完整描述所带来的不确定性的能力。Sengur和郭(2011年)设计了一种c‐k‐均值聚类方案,通过同时将图像的小波域特征和纹理信息转换到NS域。在NS域中利用熵来估计图像的不确定性;随后,提出了c‐K‐均值进行了聚类。此外,莫汉、克里希纳文尼和郭(2015)在磁共振脑肿瘤图像上提出了一种基于中智集的K均值聚类技术,并实现了非局部中智维纳滤波器以提高图像质量。郭和程(2009)通过将图像映射到NS域,并使用三个隶属集T、I和F分别表示真实度、不确定性与假度,应用基于NS的K‐均值聚类进行图像分割。此外,还采用了两个算子来降低NS过程中的不确定性,以实现有效的聚类。
在先前基于中性集的图像处理研究中,采用了一种高通滤波器(即索贝尔滤波器),其掩码尺寸为 3×3,用于定义中智集隶属函数。因此,本章节包含了对在计算中性集I中的不确定性(不确定性)子集时所使用的边缘检测滤波器的形状和尺寸的比较研究。本研究涉及了不同的滤波器,即索贝尔滤波器、普鲁伊特滤波器和非锐化滤波器,并采用了不同的掩膜尺寸。为了研究滤波器对聚类过程的影响,本研究采用了基于中智集的K均值聚类,其中像素根据其T和I的值进行聚类。此外,所提算法应用于国际皮肤影像协作(ISIC)2016挑战赛数据集的皮肤镜图像中的精确病灶区域分割(国际皮肤影像协作,无日期)。
其余部分结构如下。第2节介绍了在中性集NS的不确定性中性子集I的滤波器设计计算中所提出的比较研究的方法论。第3节包含结果、比较研究和讨论。最后,结论在第4节中给出。
2 方法论
由于皮肤镜图像的不一致结构以及噪声/伪影/气泡/浓密毛发的存在,皮肤病变聚类与分割具有挑战性。此外,皮肤病变皮肤镜图像中色素性病变区域与背景之间存在平滑的颜色过渡。为了实现精确诊断,研究人员致力于实施高效的聚类、分割和分类方法,以克服皮肤镜图像中的不确定性和模糊性€基于中性集(阿尔贾纳比、奥佐克、拉赫比和阿卜杜拉(2018);阿舒尔、郭、库楚库拉赫利、埃尔多格穆斯和波拉特,2018年;阿舒尔、哈瓦斯、郭和瓦哈巴,2018年;卡斯蒂留霍斯、波诺马里约夫、尼诺‐德‐里维拉和戈利科夫,2012年;塞莱比和佐恩伯格,2014年;达拉尔等,2011年;艾姆雷·塞莱比等,2007年;戈´梅兹、布塔科夫、埃尔什博尔和斯托克,2008年;郭、阿舒尔和斯马兰达奇,2018年;科卡拉、梅特、陈和阿伊丁,2010年;科罗特科夫和加西亚,2012年;梅利、格拉纳和库基亚拉,2006年;奥利维拉等,2016年;苏克波萨罗姆,2009年;瓦哈巴、阿舒尔、郭、拿破仑和埃尔纳比,2018年;瓦哈巴、阿舒尔、拿破仑、埃尔纳比和郭,2017年;威顿、萨德吉、李和艾特金斯,2009年;袁、斯图和祖里达基斯,2009年)。由于皮肤病变具有球状形态,本章节采用中性集K‐均值聚类算法,因为它相比层次式聚类算法能够形成更紧密的聚类。通常,K‐均值聚类因其高效性和简洁性在许多应用中发挥着重要作用。然而,为了减少皮肤镜图像中的不确定性,在聚类阶段之前必须先将图像映射到NS域。
在本章节中,使用不同的高通滤波器来计算NS域中的不确定性中性子集I。相应地,研究了改变滤波器(算子)设计对不确定性子集I计算的影响,以进一步利用中智K均值(NKM)聚类进行皮肤病变分割。NS的 α-均值操作的优化值用于降低图像的不确定性。因此,在本研究中,使用了通过遗传算法(GA)在同一皮肤镜图像数据集上获得的 αoptimal¼0.0014(阿舒尔、哈瓦斯等,2018)。该αoptimal被用作阈值,以确定将参与平均滤波操作的像素点。最后,在I集中使用另一个阈值来选择具有低不确定性值的像素,用于聚类过程。随后,使用K均值聚类方案对皮肤镜图像进行聚类,以分割皮肤病变区域。
2.1 中性图像
中智学是中性集、中智统计、中智逻辑和中智概率的基础,该理论由斯马兰达奇(1999,2003)提出。中智学理论基于任意实体 与其对立面<反B>以及<非B>之间的关系,其中 既不为<反B>,也可表示为<中性B>。作为对经典集、模糊集和区间值模糊集的推广,中性集(NS)被引入以描述信息中的不确定性和不确定性。对于NS中的任何事件 ,定义了三个隶属集(中性成分)。这些MF用于估计真值度、不确定性(既不为真也不为假)和假度,分别表示为T、I 和 F。这些中性子集用于将图像映射到中性集空间以生成NS图像。任何图像都通过计算每个像素R(j, k)的三个子集T、I 和 F(即{T(j, k), I(j, k),F(j, k)})转换为其中性图像,记作< T, I, F>(程,单,居,郭,& 张,2010)。
在本文中,为了在NS域中识别皮肤病变, 被视为皮肤镜图像中的病灶, 用于表示病灶边界,而 表示背景。因此,中性集成分T、I和F分别用来表示 、< Neut‐B>和 ,其中 和 包含区域信息, 包含边界信息。
在中性图像中,一个像素可以表示如下:
$$ R(t, i,f) = { T(j, k), I(j, k), F(j, k) } $$ (1)
其中,R(t, i, f) 是像素 R(j, k) 在 NS 域中的映射形式。t 的百分比表示病灶(真子集),i 的百分比表示边界(不确定子集),f 的百分比表示背景(假子集),即 t∈T, i∈I, 和 f∈F。对于图像 R,中性成分的三个子集(T(j, k)、I(j, k) 和 F(j, k))可基于像素 (j, k) 的像素强度值 R(j, k) 表示如下:
$$ T(j, k) = \frac{R(j, k) - R_{min}}{R_{max} - R_{min}} $$ (2)
其中Rmin和Rmax分别为最小和最大强度值。此外,中性子集F可表示为:
$$ F(j, k) = 1 - T(j, k) $$ (3)
最后,第三个不确定中智子集I,用于表示边界信息(图像中对象之间的边缘),可由以下方式给出:
$$ I(j, k) = \frac{\zeta(j, k) - \zeta_{min}}{\zeta_{max} - \zeta_{min}} $$ (4)
其中 ζmin和 ζmax分别为最小和最大绝对差值。此外, ζ(j,k)表示原始图像在相同像素位置处强度值的局部均值,可由以下公式给出:
$$ \zeta(j, k) = \sum_{c=k-m/2}^{k+m/2} \sum_{l=j-m/2}^{j+m/2} R(c, l) * S(c, l) $$ (5)
其中,S(c,l) 是用于获取差值的高通滤波器,m 是滤波器(窗口/掩码)的大小,R(c,l) 是掩码过程中的局部图像。该高通滤波器主要用于计算中性图像 I(j,k) 的不确定性,本文研究了其不同类型/尺寸的滤波器。由于中性图像的熵表示中性集空间中的元素分布,当元素分布趋于均匀时,I 的熵会增加,I 的熵按如下方式计算:
$$ Ent_I = - \sum_{i=min{I}}^{max{I}} pr_I(i) \ln(pr_I(i)) $$ (6)
其中,prI(i) 是 I 中性子集中元素的概率。随后,T 和 F 的变化应影响元素的分布以及 I 的熵,以使 T 和 F 与 I 相关联,其中 I 用于计算中性图像的不确定性。
2.2 用于I子集梯度计算的高通滤波器
本研究比较了在计算I子集(见公式4)和(5)时所使用的不同类型/尺寸的梯度滤波器(高通滤波器)S(c,l)。为了在中性集空间中准确表示原始皮肤病变图像,选择用于公式(5)中的滤波器类型和尺寸至关重要,这些参数用于进一步高效地表示子集I(j,k),该子集用于衡量中性图像R(t,i,f)的不确定性。这启发了本章节的新颖贡献,即研究不同类型/尺寸的滤波器(主要是高通算子(掩模/滤波器))在计算中性集中的I分量时的影响。随后,采用试错法确定一个阈值ThI,以利用计算得到的I子集来改进聚类过程。只有满足I ThI的像素将被排除在聚类过程之外,其聚类结果由邻近像素获得。因此,聚类过程仅对I值小于阈值的点使用T。I子集是在中性集域中为每个像素定义的。
使用不同的高通滤波器计算梯度以求得I子集的比较研究,通过皮肤镜图像最终的中性集K‐均值聚类结果进行评估。通常情况下,尺寸为 3×3的索贝尔滤波器是先前NS研究中不同图像处理应用中的默认滤波器(阿舒尔、哈瓦斯等,2018)。因此,本研究包含了不同尺寸(3×3、 5×5、 7×7和 9×9)的索贝尔、普鲁伊特和非锐化滤波器。以下简要介绍每种滤波器(阿纳杜赖,2007;皮塔斯,2000;普鲁伊特,1970;所罗门和布雷克恩,2011)。
2.2.1 索贝尔算子
不同窗口(掩模)大小的索贝尔滤波器(HSobel)可以表示如下。在大小为 3×3时,Hsobel(3×3)给出为:
| 1 | 2 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 2 | 1 |
在尺寸 5×5 下,Hsobel(5×5)定义为:
| 1 | 4 | 4 | 6 | 4 | 1 |
|---|---|---|---|---|---|
| 2 | 2 | 8 | 12 | 8 | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 8 | 12 | 8 | 2 |
| 1 | 1 | 4 | 6 | 4 | 1 |
2.2.2 普鲁伊特算子
普鲁伊特算子是一种离散微分算子,用于计算图像强度函数的梯度估计,其输出为等效梯度向量或梯度向量的范数。它在水平/垂直方向上使用可分离、整数且小数值的滤波器对图像进行卷积运算。具有不同窗口(掩码)尺寸的普鲁伊特滤波器(H Prewitt)可表示如下。在尺寸 3×3时,H Prewitt ( 3×3 )定义为:
| 1 | 1 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
在尺寸 5×5 下,HPrewitt(5×5) 定义为:
| 1 | 2 | 2 | 3 | 2 | 1 |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 3 | 2 | 1 |
| 1 | 1 | 2 | 3 | 2 | 1 |
2.2.3 非锐化算子
非锐化滤波器主要是一种锐化算子,通过从原始图像中减去经过平滑/非锐化的图像形式来增强图像中的高频分量和边缘。假设将原始图像 f(x,y) 输入到非锐化掩模中,因此生成的边缘图像 d(x,y)(包含高通分量)可表示如下:
$$ d(x, y) = f(x, y) - f_{lowpass}(x, y) $$ (7)
然后,通过使用以下表达式将边缘图像加回到原始图像中以进行锐化:
$$ f_{sharp}(x, y) = f(x, y) + s * d(x, y) $$ (8)
其中s是缩放常数。具有不同窗口(掩模)大小的非锐化滤波器(H Unsharp)可以表示如下。在大小为3×3时,HUnsharp(3×3)由以下给出:
| 1/16 | 2/16 | 1/16 |
|---|---|---|
| 2/16 | 12/16 | 2/16 |
| 1/16 | 2/16 | 1/16 |
在尺寸 5×5 下,HUnsharp ( 5×5 )由下式给出:
| 1/32 | 0 | 2/32 | 0 | 1/32 |
|---|---|---|---|---|
| 0 | 1/32 | 2/32 | 1/32 | 0 |
| 2/32 | 2/32 | 24/32 | 2/32 | 2/32 |
| 0 | 1/32 | 2/32 | 1/32 | 0 |
| 1/32 | 0 | 2/32 | 0 | 1/32 |
2.3 基于均值滤波器的中性集用于K‐均值聚类
在NS过程中,I子集通过识别将在下一个NS版本中被考虑的像素,用于在下一个NS版本中修改真子集T。因此,在识别过程中采用一个阈值(αoptimal¼0.0014),其中使用局部均值来处理I值高于 αoptimal¼0.0014的像素。T(j,k)的局部均值可表示为:
$$ T_{local}(j, k) = \frac{1}{n*n} \sum_{c=k-n/2}^{k+n/2} \sum_{l=j-n/2}^{j+n/2} R(c, l) $$ (9)
然后,使用以下表达式对 T 中使用的像素强度进行更新:
$$ T_{updated}(j, k) =
\begin{cases}
T_{local}(j, k), & I(j, k) > \alpha_{optimal} \
T(j, k), & I(j, k) \leq \alpha_{optimal}
\end{cases} $$ (10)
这个更新后的值用于生成图像的迭代新版本,具体如下:
$$ R_{modified}(j, k) = R_{min} + (R_{max} - R_{min}) * T_{updated}(j, k) $$ (11)
因此,I的熵被用作NS迭代过程的停止准则,可定义为:
$$ \frac{|Ent_I(i) - Ent_I(i+1)|}{Ent_I(i)} < delta $$ (12)
2.4 提出的中性集K‐均值聚类
通常,K‐均值聚类被认为是最高效的无监督分割技术之一。它将对象/像素/数据点聚类到K个组中,同一组内数据点之间的距离较小(Dhanachandra,Manglem,& Chanu, 2015)。K‐均值方法是一种迭代过程,用于计算每个聚类的平均值,并计算每个点到其匹配聚类(即最近的聚类)的距离。该迭代过程将持续进行,直到每个聚类中平方误差总和无法进一步减少为止。
在改进的中性图像中,另一个阈值 ThI用于确定进一步聚类过程的像素点。该阈值 ThI会影响皮肤病变图像的聚类过程,因为它被用来识别不确定性像素其 I 值高于该阈值。只有 I 中满足 I(j,k) <ThI 的像素才会被用于 T 中,通过 K‐均值方法进行进一步聚类。其他像素将不参与 K‐均值聚类过程,其聚类结果将根据其邻域的聚类结果确定。
因此,以下算法报告了基于不同边缘检测的中性集对K‐均值聚类影响的比较研究的各个阶段。
算法:提出的比较研究流程
- 开始
- 输入皮肤镜彩色图像
- 将彩色皮肤镜图像转换为灰度图像
-
中性集映射过程
- 设置 α最优 ¼0.0014 以及迭代次数 ¼100
- 选择高通滤波器(Sobel、Prewitt 或 unsharp)用于在 I 计算过程中进行梯度计算的比较研究
- 对每个选定的滤波器尝试不同的窗口(掩模)大小,从尺寸集合 3×3 , 5×5, 7×7 和 9×9
- 在灰度图像上计算第一个中性集的三个中性子集 T、I 和 F
- 在灰度图像上 计算第一次 I(第一次迭代)的熵
- 开始中性集的迭代步骤,具体如下:- 步骤1:计算 T、I 和 F
- 步骤2:使用前一次I生成下一个T(更新后的T)和 αoptimal
- 步骤3:生成新图像版本 Rmodified
- 步骤4:计算熵
- 如果达到停止条件 → 中断
- Else → 转到步骤1
- 结束条件:NS过程的停止
- 使用K‐均值在T上对I(j,k) <ThI的选定像素进行聚类(聚类过程)
- 使用其邻居的聚类结果对标记像素 I(j,k) ≥ThI(聚类结果)
- 停止
在本研究中,利用中性图像成分对皮肤病变图像中的像素进行聚类,将具有最低T值的聚类视为病灶候选像素。此外,I的精确计算有助于准确确定病灶边界,这主要取决于滤波器类型和大小,如本研究中所示。
2.5 评价指标
在本章节中,采用了几种评价指标(Rundo等,2017年),即 JAC、Dice系数(Dice)、特异性、灵敏度和准确率,用于评估在中性集的中智集I分量计算过程中使用不同边缘检测滤波器时,基于 NS的K均值聚类过程的性能。这些指标包括JAC指数,它是一种统计测量,可表示如下:
$$ JAC(O, Q) = \frac{ArO \cap ArQ}{ArO \cup ArQ} $$ (13)
其中[是并集操作,\是任意两个集合的交集操作,ArO表示使用基于NS的K均值聚类得到的聚类/分割的皮肤病变区域,ArQ是真实皮肤病变区域。较高的JAC值相比低JAC值表示更优的结果,当 JAC ¼1时表示完全相似,JAC ¼0时表示无相似性。
此外,Dice指数(Dice)使用以下公式来比较两组G和Z之间的对应关系:
$$ Dice = \frac{2|G \cap Z|}{|G| + |Z|} $$ (14)
与检测到的病变区域相关的其他性能指标包括准确率、敏感度和特异性。准确率用于衡量真阳性/阴性结果的比例,以明确诊断程度的可靠性。敏感度用于衡量所用聚类方法对皮肤病变区域的检测预测能力。而特异性则反映所提出的聚类方法对皮肤镜图像中其他区域的预测情况。
3 结果与讨论
在本章节中,从ISIC 2016挑战赛中随机选取了50幅皮肤病变图像,用于评估在NS中进行子集计算时所使用的不同滤波器与各图像对应的真实标签之间的差异。I最优值 α optimal¼ 0.0014,如Ashour, Hawas 等人 (2018) 所得出的结论,在性能评估计算过程中被采用。
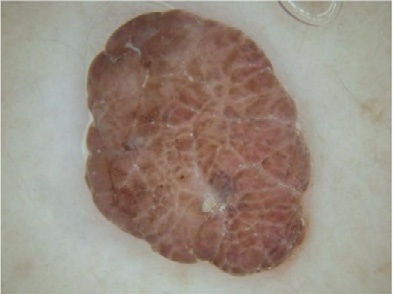
图1
使用大小为 7×7的非锐化滤波器的所提方法步骤:(A) 原始ISIC_0010447皮肤镜图像,(B) 去毛预处理后的图像,(C) 预处理图像的灰度版本,(D) 第一次迭代后的首个中性版本,(E)–(H) 最后一次迭代后的中性映射算子,分别为 (E) 最终真值图像T;(F) 最终不确定图像I;(G) 最终假值图像F;(H) 最终中性版本,(I) 输出的中性图像,(J) K均值聚类图像(无监督分割图像)。
图1展示了使用大小为 7×7的非锐化掩模滤波器进行中性映射时各阶段的相应图像。图1D显示了首先生成三个子集T, F,和I的皮肤镜中性图像,在第一次迭代后所示,其中在下一次迭代之前计算了熵值。随后,创建了这三个子集,并计算其熵值,与先前获得的熵值进行比较。此过程反复执行,直到最近一次迭代的熵值与其先前熵值之间的差异除以前一个熵值小于 α optimal¼ 0.0014,即
$$
\frac{|Ent_I(\text{迭代}e+1) - Ent_I(\text{迭代}e)|}{Ent_I(\text{迭代}e)} < delta
$$
满足条件,则终止迭代过程,并得到NS图像的最终T、F和I算子,如图1E–H所示。T, F, 和 I算子的中性集图像结果如图1E–H所示。
3.1 在NS域中设计中性集I子集时不同滤波器的比较研究
本研究中基于K均值的无监督分割用于检测和聚类所选皮肤镜图像,如图2 所示,使用了不同尺寸的边缘检测滤波器。图中图像具有不同的病灶大小、形状和皮肤表面粗糙度。图2C–E分别展示了使用索贝尔滤波器、普鲁伊特滤波器和非锐化掩模滤波器得到的聚类图像。红色轮廓表示ISIC 2016数据集中提供的相应皮肤病变的真实标签,而蓝色轮廓表示使用基于NS的K均值聚类结合不同结构的边缘检测滤波器检测到的皮肤病变区域。
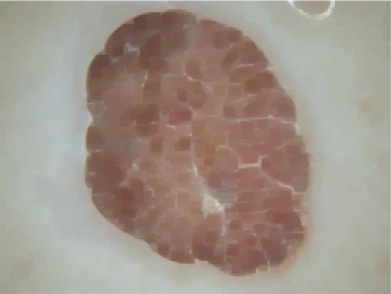
图2
表明,使用窗口大小为 7×7的非锐化滤波器相较于同一滤波器的其他窗口大小以及其他滤波器类型(即Sobel和Prewitt算子)均取得了更优的结果。这些结果归因于非锐化滤波器能够锐化并增强高频分量,而高频分量代表了皮肤镜图像中的边缘。然而,所有滤波器在不同窗口大小下均未能识别ISIC_0010447皮肤镜图像中由同一病灶部分存在不同颜色区域和/或暗色区域引起的皮肤病变轮廓。
3.2 性能评估
在本次比较研究中,测量了中性集映射过程中受所使用的边缘检测滤波器及其尺寸影响的评价指标以及所需的计算时间。
3.2.1 评价指标测量
在中性集设计中,使用不同边缘检测滤波器测得的评价指标的平均值如 表1 所示。
表1 使用不同边缘检测滤波器的各性能评价指标的平均值
| 滤波器类型/大小 | JAC | Dice | 敏感度 (%) | 特异性 (%) | 准确率 (%) |
|---|---|---|---|---|---|
| Sobel 7x7 | 0.75 | 0.85 | 78.70 | 96.62 | 91.87 |
| Prewitt 5x5 | 0.76 | 0.85 | 79.14 | 96.62 | 91.96 |
| Sobel 9x9 | 0.76 | 0.85 | 79.16 | 96.62 | 91.96 |
| Sobel 5x5 | 0.76 | 0.85 | 79.18 | 96.62 | 91.96 |
| Prewitt 7x7 | 0.76 | 0.85 | 79.28 | 96.62 | 92.01 |
| Prewitt 9x9 | 0.76 | 0.85 | 79.49 | 96.62 | 92.12 |
| Unsharp 3x3 | 0.78 | 0.87 | 78.10 | 99.95 | 95.09 |
| Sobel 3x3 | 0.78 | 0.88 | 78.68 | 99.95 | 95.07 |
| Prewitt 3x3 | 0.78 | 0.88 | 78.69 | 99.95 | 95.07 |
| 非锐化 5x5 | 0.79 | 0.88 | 78.93 | 99.95 | 95.19 |
| 非锐化 9x9 | 0.79 | 0.88 | 78.95 | 99.95 | 95.19 |
| 非锐化 7x7 | 0.80 | 0.89 | 79.14 | 99.95 | 95.25 |
表1 证明了非锐化掩模滤波器在 7×7窗口大小方面具有优越性,其平均准确率为95.25%,JAC为0.80,且在检测皮肤病变区域时Dice为0.89,优于使用其他不同尺寸滤波器的结果。然而,在特异性方面,最佳平均值为99.95%,该值是使用窗口大小为 3×3、 5×5、 7×7和以及Sobel尺寸为 3×3和Prewitt尺寸为 3×3的情况下的非锐化滤波器获得的。此外,尺寸为 9×9的Prewitt滤波器达到了最佳平均敏感度79.49%。图3–5展示了表1中报告的结果。
这些实验结果证明了在不同窗口大小下,与其他边缘检测滤波器相比, 7×7的非锐化滤波器在检测皮肤病变区域边界方面具有整体优越性。
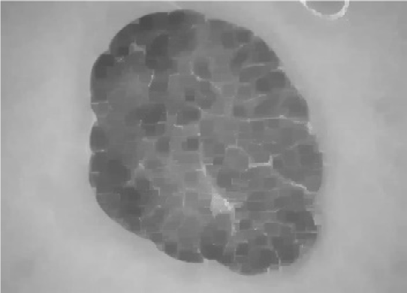
图3
使用不同边缘检测滤波器的JAC和敏感度的比较平均结果。
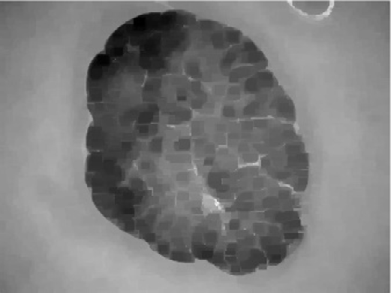
图4
使用不同边缘检测滤波器的特异性和准确率的比较平均结果。
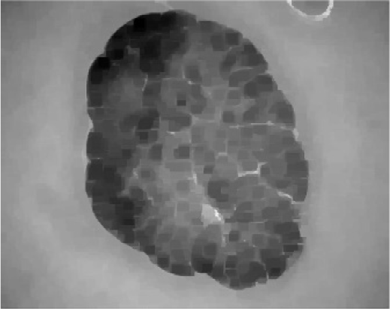
图5
使用不同边缘检测滤波器的比较平均骰子值。
3.2.2 基于计算时间的对比研究
计算时间是计算I子集时需要考虑的另一个指标。随后,通过测量NS过程的计算时间,以比较不同尺寸的滤波器之间的差异。因此,图6 展示了在中性集平均处理时间(秒)的比较研究(Y轴)。
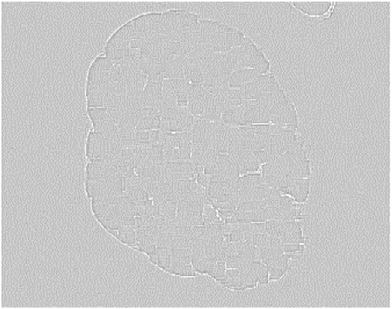
图6
显示,窗口大小为 3×3的非锐化掩模滤波器所需的计算时间为最少,为1.74秒,而尺寸为 7×7的普鲁伊特算子所需计算时间最长,为7.06秒。然而,窗口大小为 7×7的非锐化滤波器耗时5.07秒。此外,其他滤波器结构的计算时间在4.2–6秒之间。
上述结果确立了研究NS过程中所用边缘检测滤波器设计的重要性,以确保获得清晰的检测边界。因此,建议研究改变滤波器类型和大小对不同医学图像类型(如磁共振图像、超声图像和显微图像)的影响,以确定在NS中使用的最合适滤波器结构。同样,如图2所示,所有滤波器的性能均下降,未能检测到包含不同颜色区域和/或暗色区域的皮肤病变区域。因此,建议实现一种新滤波器以应对此类情况。在未来工作中,还建议研究不同滤波器类型/大小在计算中性集的三个主要组成部分(T、I、F)时的影响,而不仅限于I子集中的滤波器。其他聚类技术如NCM也可应用于此类比较研究,并与 K‐均值进行比较。
4 结论
图像聚类在无监督分割中对多种应用起着至关重要的作用,尤其是在医学图像处理中。在聚类过程中,像素根据其邻近的像素位置被划分到不同的属性区域。其中一项迫切的医学聚类应用是皮肤病变的检测与分割,这需要早期且高效的诊断。由于皮肤病变对比度低、黑色素瘤存在类内不一致性,以及皮肤镜图像中存在气泡、毛发和噪声等各种伪影,自动化黑色素瘤检测与分割被视为具有挑战性的过程。
大量基于图像处理的研究被开展,以处理皮肤镜图像实现精确诊断。这些研究建议使用中智理论来降低或消除皮肤镜图像中的不确定性。本章节的引言部分提到了一些采用中性集(NS)进行皮肤病变检测、聚类、分割和分类的研究。然而,这些研究均未探讨滤波器类型和大小在计算中性集(T、I、F)三个主要分量时的影响。这促使了本章节的近期工作针对广泛使用的默认滤波器(即大小为 3×3的索贝尔滤波器)开展此类比较研究。此外,通过计算分割指标(即JAC、骰子、特异性、敏感度和准确率)以及每个滤波器的计算时间,评估了使用不同滤波器结构和大小的效果。
在本次研究中,从公开的ISIC 2016数据集中随机选取皮肤镜图像进行所提出的比较研究。在将彩色皮肤图像转换为灰度后,应用预处理步骤,然后使用三个中性子集将皮肤镜图像映射到中智集域,这三个中性子集分别表示皮肤镜图像中的病灶区域信息、病灶边界和背景。在该映射过程中,如所提出的方法,考察了不同类型和尺寸的多种边缘检测滤波器结构。最后,通过K均值聚类过程对映射后的中性图像进行分割。
比较实验结果证明,使用窗口大小为 7×7的非锐化掩模滤波器在NS过程中表现出色,耗时5.07秒,在皮肤病变区域检测中实现了平均JAC为0.80、Dice为0.89、准确率为95.25%的最佳性能,优于默认大小为 3×3的Sobel滤波器以及其他不同尺寸的滤波器。因此,建议在未来工作中使用Roberts和Laplacian等其他算子。
 中性集在医学图像聚类中的应用
中性集在医学图像聚类中的应用




















 33
33

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








