基于聚类的分布式信源编码

分布式信源编码方法研究基于聚类无线传感器网络

1 引言

无线传感器网络（WSN）具有低成本和低复杂度的特点，具备良好的易于扩展特性。无线传感器网络在工业、农业、医疗服务以及环境监测和智能仪表等领域中发挥着广泛而重要的作用（Akyildiz 等，2002；Mainetti 等，2011）。

无线传感器网络采用大量低功耗无线传感器作为基本单元，通过自组织方式进行路由，并将采集到的数据传输至一个汇聚节点。由于节点依靠自身电池供电，而电池在部署后难以更换，因此一旦电池耗尽，网络的连通性将受到影响，甚至可能导致网络拥塞。

如果节点断电则会崩溃。因此，在由有限能量传感器节点组成的无线传感器网络（WSN）的发展过程中，如何延长网络寿命成为一个重大问题（Mainetti 等，2011）。

在网络部署过程中，为了提高测量精度和网络鲁棒性，通常采用密集部署，这会导致测量数据之间存在高空间相关性（Chou 等，2004）。例如，在某些地理区域中，温湿度监测甚至移动车辆跟踪等应用会产生大量冗余信息（Chou 等，2004）。由于无线传感器网络的功耗主要集中在数据通信上，冗余信息的通信将导致巨大的能量浪费。分布式信源编码使得相关信源在无需任何交叉通信的情况下实现独立编码。同时，分布式信源编码实现了与存在交叉通信时相同的数据压缩效果，消除了信息冗余并延长了网络寿命。

基于簇的路由是实现传感器网络高效率的另一种重要方法（海因策尔曼，2000）。无论理论还是实验均表明，基于簇的路由能够提高能量效率。通过聚类算法，基于簇的路由实现了无线传感器网络中的节点分层。数据采集和通信被分配给不同的节点，从而平衡网络中的能量消耗，达到延长网络寿命的目的（袁等人，2008）。

分布式信源编码（DSC）应将每个独立信源的所有数据传输到统一解码器进行联合转码。这种多对一结构使得DSC的工作方式与基于簇的无线传感器网络（WSN）相同，从而为DSC与基于簇的路由相结合以及实现采样数据压缩提供了可能。在文献（埃尔‐沙布拉维和穆尼尔，2010；托莱多和王，2010；袁等人，2008）中，提出了若干将DSC应用于聚类网络的方案。然而，其中一些方案仅从相邻节点收集数据，压缩效率较低；另一些方案则未能详细说明相邻节点间互相关的应用。针对上述不足，提出了一种基于残差值编码的新型分布式信源编码算法。该算法降低了转码的复杂度，同时由于充分利用了各信源之间的相关性，提高了压缩比，并延长了网络寿命。

2 分布式信源编码的改进的残差值编码

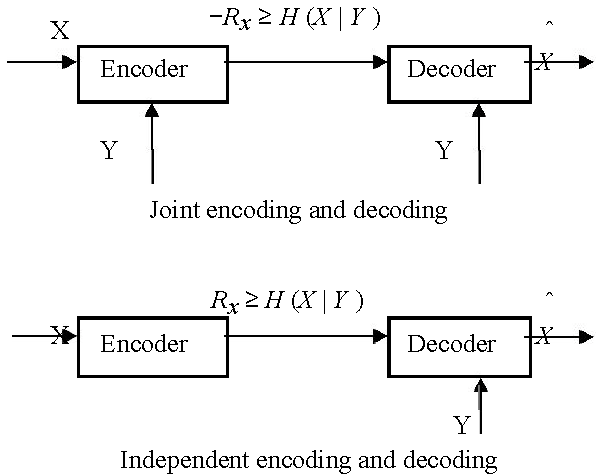
Slepian‐Wolf提出的DSC理论核心概念是：两个互相关信源X和Y在进行编码时（Slepian和Wolf，1973），如果彼此知道互相关信息（如联合概率分布），则无论X是否已知Y，都能获得相同的编码效率。也就是说，图1所示的不同编码方式下的结果是相同的。由于在独立方案中无需与Y通信，因此DSC不仅具有极大的灵活性，而且通信功耗较低。这对于能量受限的无线传感器网络非常具有吸引力。

在斯莱皮安‐沃尔夫理论中，Y被定义为边信息。如果对X和Y进行独立编码，并能实现无失真的联合解码，则必须满足以下条件：

$$
\begin{cases}
R_x \geq H(X|Y) \
R_y \geq H(Y|X) \
R_x + R_y \geq H(X,Y)
\end{cases}
$$

Rx和Ry分别表示X和Y的编码率。H(X|Y)和H(Y|X)表示相应的条件熵。H(X,Y)表示X和Y的联合熵。针对互相关信源，即使扩展到多相关信源（Xiong 等人，2004），斯莱皮安‐沃尔夫理论仍处于理论阶段，直到1999年DISCU算法（Pradhan 和 Ramchandran，2003）被提出。至今已出现许多实用的分布式信源编码方案，例如基于校验子的分布式信源编码（Pradhan 和 Ramchandran，2003）、采用Turbo码或LDPC码的方案（王等人，2012；哈卢什和达瓦德赫，2013；华和陈，2008）以及基于残差值的分布式信源编码（Chou 等，2004）等。在温度、湿度、流量和压力监测等应用中，由于不同传感器测量数据之间存在有限容差且参数为连续可变参数，表现出互相关性，基于残差值的分布式信源编码相比其他方法具有优越性。

2.1 残差值编码

考虑到在温度监控中的应用，数据范围设置为 [min s, max s]，监控精度为 ∆（根据实际应用需求而定，例如可以是 0.1°C）。比特数据为 n。可能的样本监控集合为 { | = = + ⋅∆ ∈ …− 0,1,, 2 1 n min,(())i is s s i iΩ}。根据周等人（2004），如果 X 与 Y 之间的差值小于 2k–1 ∆(0 ≤ k ≤ n)，则 X 可以用 k 比特进行编码，以实现数据压缩。残差值编码的公式如下：

$$
f(X) = \text{index}(X) \mod 2^k
$$

其中，f(X) 表示 X 编码的结果，index(X) 表示 X 在 Ω 中的顺序（从零开始）。计算公式如下所示：

$$
\text{index}(X) = \frac{X - s_{\text{min}}}{\Delta}
$$

来自X编码的相同数据可以被归类到一个集合中，该集合称为陪集。如果f(X)作为该陪集的索引，则陪集的数量为2k，其元素可以是 2n–k。利用边信息 Y 和从 f(X) 恢复出的接收端真实信源 X，可通过以下公式进行解码：

$$
\hat{X} = \min_{r_i \in S} |Y - r_i|
$$

在此公式中，$\hat{X}$ 表示解码结果，而 $S$ 表示由 f(X) 和 ri 推导出的陪集，其中 i 表示陪集中的元素。

上述过程较为简单，因为它仅涉及数据计算，其复杂度为O(1)。解码是在陪集中进行搜索的过程。通过元素的有序排列，平均复杂度与陪集中的元素数量成正比，即O(2n–k)。采样值越大，解码的复杂度越高。

2.2 分布式信源编码的改进的残差值编码

该算法的编码方式与残差值编码相同，不同的解码过程如下所示。

1 两个互相关信源的编码

由于X和Y是来自集合Ω的样本，当获得编码数据f(X)后，可通过公式(5)得到X和Y的位置差异。因此，可根据边信息Y按照公式(6)实现解码。

$$
\delta = \text{index}(X) - \text{index}(Y)
$$

$$
\hat{X} = Y + \delta \cdot \Delta
$$

由公式(2)可得以下结论：

$$
f(X) = \text{index}(X) \mod 2^k
$$

$$
f(Y) = \text{index}(Y) \mod 2^k
$$

由上述方程可得：

$$
\text{index}(X) = 2^k \alpha_x + f(X)
$$

$$
\text{index}(Y) = 2^k \alpha_y + f(Y)
$$

其中αx和αy为非负整数。

由公式(5)、(9)、(10)可得公式(11)

$$
\delta = (\alpha_x - \alpha_y)2^k + f(X) - f(Y)
$$

由于X与Y之间的差值小于 2k–1 ∆，这意味着 |\alpha_x – \alpha_y| ≤ 1，也就是说， |\alpha_x – \alpha_y| 的值只能是0或1。

• 如果|f(X) – f(Y)| < 2k− 1且|\alpha_x – \alpha_y| = 1，则可推出|\delta| = |(\alpha_x – \alpha_y)2k+ f(X)− f(Y)| ≥ |(\alpha_x – \alpha_y)2k| –|f(X) – f(Y)> |2k – 2k–1| = 2k− 1。但此结果与 |\delta| < 2k− 1矛盾。因此，|\alpha_x – \alpha_y| 的结果只能为零。由公式(11)可得δ= X′−Y′。

• 如果|f(X) – f(Y)| < 2k − 1且 |\alpha_x – \alpha_y| = 0，则可推导出|\delta| = |f(X) − f(Y)| ≥ 2k − 1。此结果与 |\delta| < 2k − 1矛盾。因此，|\alpha_x − \alpha_y| 的结果只能是1。如果\alpha_x – \alpha_y 与 f(X)− f(Y) 符号相反，然后推导出 |\delta| = 2k+ |f (X)− f(Y)| > 2k −1。这与 |\delta| < 2k −1 相矛盾。因此容易证明 \alpha_x – \alpha_y 以及 f(X) – f(Y) 的符号必须相同。由上述分析可得以下公式：

$$
\delta = \frac{(f(X) - f(Y))}{2^{k-1}} \cdot (f(X) - f(Y))
$$

$$
\delta =
\begin{cases}
f(X) - f(Y), & |f(X) - f(Y)| < 2^{k-1} \
2^k - |f(X) - f(Y)|, & |f(X) - f(Y)| \geq 2^{k-1}
\end{cases}
$$

2 多个相关信源编码

编码方案描述如下：
如果信源Xi根据边信息Xj进行编码，则称Xj为Xi的参考信源。假设有多个相关信源(X1, X2,…, Xn, Y)，其中Y是边信息，X1, X2,…, Xn是需要编码的信源。在交叉相关矩阵中，mij表示Xi与Xj之间的相关性。S 表示编码信源集合，而S′表示已编码信源。R表示参考信源集合，E为编码结果。现在开始编码。

i 清空R和E。将所有编码信源X1, X2,…, Xn 放入S中，并将边信息Y放入S′中。ii 从S和S′中选择满足 arg max mij, i≠j, xi∈S, xj∈S′的Xi和Xj 。iii 将Xi从S移动到S′，同时将Xj移入R。

iv 在两个相关信源的原则下对与Xi相关的信源进行编码，并将结果f(Xi)放入E。v 重复步骤 ii 到 iv 直至 S 为空。

vi 从S′中删除Y。

解码方案描述如下：此处，D被定义为解码结果集合。

i 将E放入 D 中。ii 分别选取E和 R 的第一个元素，记为e和r；对与 D 中参考信源相关的e进行解码，并将结果放入D中。然后删除e和r。iii 重复步骤 ii 直至E和 R 均为空。iv 从D中删除Y，并对D进行自然排序以获得解码结果。

3 残差值编码算法在聚类无线传感器网络中的应用

由于聚类无线传感器网络的结构有利于分布式信源编码算法的运行，我们考虑将改进的编码算法应用于LEACH‐C聚类路由协议中以提高网络性能（海因策尔曼，2000）。

在LEACH‐C协议中，无线传感器网络的运行分为两个阶段，即簇的建立阶段和就绪阶段。建立阶段可分为四个部分，分别是竞争簇头、簇头广播、成员加入和广播调度。

• 在建立阶段，汇聚节点收集传感器节点的位置和能量信息。利用这些信息，根据地理距离将传感器节点划分为不同的簇，并选择簇头。随后，将簇信息广播到网络中，以便在节点上形成簇。簇头将分配时隙频率向其管辖范围内的所有簇发送数据，而节点将在自己的时隙内将数据发送给簇头。

在就绪阶段，每个节点将在自己的时隙内将其采集的数据发送给簇头。一旦簇头收到来自所有簇节点的信息，便会将这些信息进行合并，并发送给汇聚节点。

利用互相关，对LEACH‐C协议进行如下改进：
簇头可以根据簇成员的相关信息计算出S和R。将S中源的顺序作为时隙顺序，并将R中对应的元素作为参考源，簇头可在簇内进行广播。每个节点将根据参考源在其各自的时隙内完成编码，并将编码后的数据反馈给簇头。随后，簇头进行解码。由于各源之间通信的数据均为已完成编码的数据，通信数据量迅速减少。通过这种方式，网络性能得到了提升。

4 实验设计与结果分析

本文比较了基于经典LEACH‐C协议和基于改进的残差值编码LEACH‐C协议的网络性能差异。实验设计采用 Heinzelman（2000）提出的相同无线通信功耗模型。
由于编解码算法较为简单，其能量消耗可忽略不计。一百个传感器随机部署在100 m²的区域中，用于温度监控。温度监测范围为[–30°C, 50°C]，精度为0.1°C。系统中有两个汇聚节点，编号分别为50和155。簇头节点数量为5个，每个节点的初始能量为1 J。其他仿真参数与El‐Shabrawy和Mounir（2010）所使用的相同。

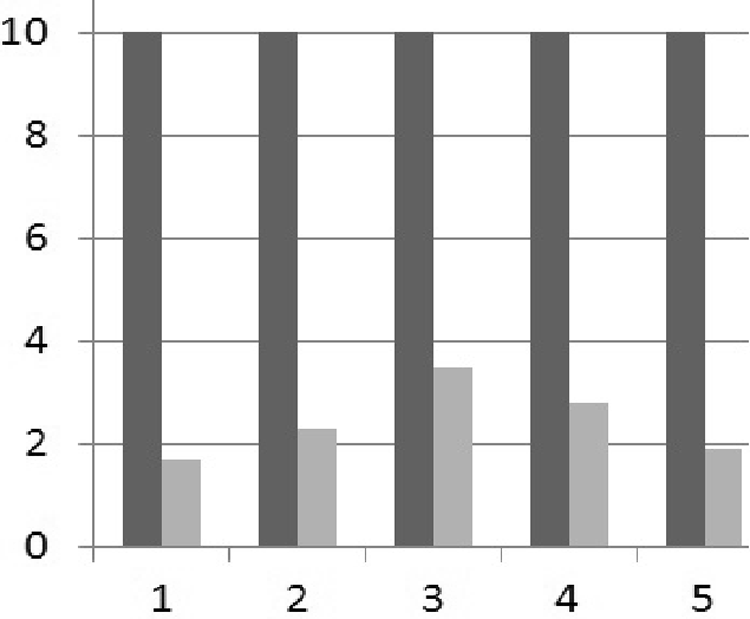
图2显示了不同簇中每个成员的平均发送比特数。它表达了LEACH‐C协议在数据压缩方面的优势，该协议使用了残差值编码算法。

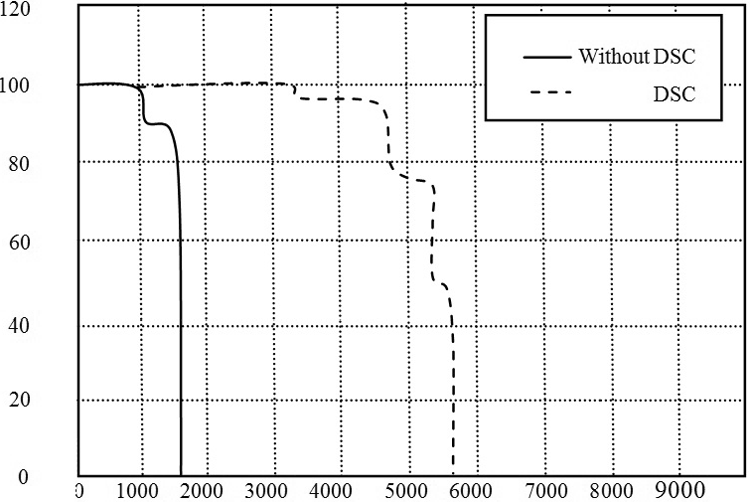
图3表明了改进的残差值编码算法对功率的影响。

5 总结

本文表明，分布式信源编码（DSC）可帮助无线传感器节点压缩通信数据，从而降低无线传感器网络（WSN）中通信时的能量消耗。在聚类无线传感器网络中，簇节点地理位置相对接近，其数据之间具有较强的相关性。
根据该特性，将分布式信源编码与LEACH‐C协议相结合，对簇内通信的数据进行压缩，以实现较低功耗的目标。
理论分析和实验结果均表明，这种结合能够延长传感器节点的寿命，进而延长无线传感器网络的寿命。