51Nod - 1242 斐波那契数列的第N项矩阵快速幂

最新推荐文章于 2020-12-13 11:04:15 发布

原创最新推荐文章于 2020-12-13 11:04:15 发布 · 187 阅读

0 ·

CC 4.0 BY-SA版权

思维专栏收录该内容

3 篇文章

订阅专栏

本文介绍了一种高效计算斐波那契数列第n项的方法，利用矩阵快速幂运算，解决了传统递归算法的时间复杂度过高的问题。通过两种实现方式展示了如何将斐波那契数列计算转化为矩阵运算，适用于处理大规模数值。

矩阵相乘(百度图片）

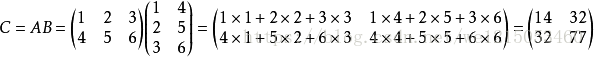
斐波那契数列的定义如下：

F(0) = 0

F(1) = 1

F(n) = F(n - 1) + F(n - 2) (n >= 2)

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)

给出n，求F(n)，由于结果很大，输出F(n) % 1000000009的结果即可。

Input输入1个数n(1 <= n <= 10^18)。Output输出F(n) % 1000000009的结果。Sample Input

Sample Output

#include<stdio.h>
#include<vector>
#include<iostream>
using namespace std;

typedef long long ll;
typedef vector<ll>vec;
typedef vector<vec>mat;


const int M = 1000000009;

mat mul(mat &a,mat &b)
{
	mat c(a.size(),vec(b[0].size()));
	for(int i=0;i<a.size();i++)
	for(int k=0;k<b.size();k++)
	for(int j=0;j<b[0].size();j++)
	{
		c[i][j]+=(a[i][k]%M)*(b[k][j]%M);
		c[i][j]%=M;
	}
	
	return c;
}

mat pow(mat a,ll n)
{
	mat b(a.size(),vec(a.size()));
	for(int i=0;i<a.size();i++)
	b[i][i]=1;
	while(n > 0)
	{
		if(n&1) b=mul(b,a);
		a=mul(a,a);
		n>>=1;
	}
	return b;
}

int main() 
{
	ll n;
	while(~scanf("%lld",&n))
	{
		mat a(2,vec(2));
	    a[0][0]=1;
	    a[0][1]=1;
	    a[1][0]=1;
	    a[1][1]=0;
	    a=pow(a,n);
	    printf("%lld\n",a[1][0]);
	}
	return 0;
}

第二种：因为不能返回数组型，所以用结构体返回

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
#define N 1000000009
#define ll long long

struct node
{
	ll a[2][2]
};

node mul(node a,node b)
{
	node c={0}; //一定要清零，否则为1
	for(int i=0;i<2;i++)
	for(int k=0;k<2;k++)
	for(int j=0;j<2;j++)
	{
		c.a[i][j]+=(a.a[i][k]%N)*(b.a[k][j]%N);
		c.a[i][j]%=N;
	}
	return c;
}

node pow(node t,ll n)
{
	node b={0}; //一定要清零
	for(int i=0;i<2;i++)
	b.a[i][i]=1;
	
	while(n>0)
	{
		if(n&1) b=mul(b,t);
		t=mul(t,t);
		n>>=1;
	}
	return b;
}

int main()
{
	ll n;
	while(~scanf("%lld",&n))
	{
		node t;
		t.a[0][0]=1;
		t.a[0][1]=1;
		t.a[1][0]=1;
		t.a[1][1]=0;
		t=pow(t,n);
		printf("%lld\n",t.a[1][0]);
	}
	return 0;
}