乘性衰落下WSN分布式检测

IEEE物联网期刊，第8卷，第11期，2021年6月1日 9059

基于广义得分检验的乘性衰落下无线传感器网络中的分布式检测

多梅尼科·丘翁佐，电气与电子工程师协会高级会员，皮耶鲁吉·萨尔沃·罗西，电气与电子工程师协会高级会员，和普拉莫德·K·瓦尔什尼，电气与电子工程师协会终身会士

摘要

在本文中，我们研究了利用无线传感器网络对非合作（发射信号未知）目标进行分布式检测的问题。当目标存在时，传感器观测到一个（未知的）确定性信号，该信号的衰减取决于传感器与目标之间的未知距离，并受到乘性衰落和加性高斯噪声的影响。为了建模物联网中的能量受限操作，采用了一位传感器测量量化，并研究了两种量化策略。融合中心通过有噪二进制对称信道接收来自传感器的比特信息，并据此提供更精确的全局推断。该模型导致一种仅在假设H1下可观测干扰参数（即目标位置xT）的检验问题。本文利用戴维斯框架设计了广义拉奥和局部最优检测（LOD）检验的广义形式。针对所提出的广义拉奥和LOD方法，还提出了一种启发式的阈值优化方法。仿真结果验证了所提方法的良好性能。

索引术语

分布式检测（DD），广义似然比检验，物联网（IoT），局部最优检测（LOD），拉奥检验，无线传感器网络（WSNs）。

一、引言

物联网（IoT）设想将数十亿个具有感知、计算和通信能力的微型设备用于日常生活，目前已成为无线通信与传感领域的改变游戏规则的技术[1],[2]。无线传感器网络（WSNs）构成了物联网的“感知臂”，其中分布式检测（DD）是一项被广泛研究的任务[3],[4]，具有多种应用，例如认知无线电系统[5],[6]或监视[7]。然而，无线传感器网络中的严格带宽和能量约束阻碍了传感器的全精度上报，传感器通常受到限制

手稿收到日期2020年7月24日；修订于2020年12月31日；接受于2021年1月27日。出版日期2021年2月2日；当前版本日期2021年5月21日。(通讯作者：多梅尼科·丘翁佐。)多梅尼科·丘翁佐隶属于意大利那不勒斯“费德里科二世”大学电气工程与信息技术系，邮编80138，意大利那不勒斯（电子邮件：domenico.ciuonzo@unina.it）。皮耶鲁吉·萨尔沃·罗西隶属于挪威科技大学电子系统系，挪威特隆赫姆，邮编7491，同时隶属于SINTEF能源研究所天然气技术部，挪威特隆赫姆，邮编7034（电子邮件：salvorossi@ieee.org）。普拉莫德·K·瓦尔什尼隶属于美国纽约州雪城大学电气工程与计算机科学系，美国纽约州雪城市，邮编13244（电子邮件：varshney@syr.edu）。数字对象标识符10.1109/JIOT.2021.3056325

向融合中心（FC）发送关于推断假设的一位信息。由于上述原因，在过去几年中，许多研究工作集中在基于一位量化测量[8]–[10]的分布式检测上。在这种情况下，传感器端的最优决策过程是对局部似然比（LR）[11],[12]进行一位量化。然而，该过程存在两个问题：第一，量化器阈值的设计复杂度呈指数增长[13],[14],；第二，由于目标参数未知[14]，无法计算传感器的似然比。因此，所报告的一位信息要么是原始测量量化的结果[15]–[17]，要么是通过次优检测统计量[18]推断出的二值事件的表示。

在这两种方案中，融合中心（FC）收集传感器生成的位，并通过适当设计的融合规则对其进行融合，以提高单传感器检测能力。在基于物联网的系统中，融合中心可以通过实现“感知即服务”范式部署在云上[19]。在条件独立假设下，最优融合规则涉及将接收到的传感器比特的加权和与阈值进行比较，其中权重取决于未知目标参数[3]。

然而，当模型为参数化指定（部分参数未知）时，融合中心面临复合假设检验问题，广义似然比检验（GLRT）通常是设计上的首选[20]。事实上，在专注于分布式检测（DD）的无线传感器网络（WSN）文献中，量化数据的GLRT融合已被广泛研究[16],[21],[22],，包括对位于未知位置的未知源（非合作目标）这一具有挑战性的情况，因为该方法所需先验知识最少。因此，一些近期研究已针对此问题展开工作[7],[15],[22]–[24]。在[22],中，提出了一种用于检测位置和发射功率均未知目标的GLRT。为了获得计算更简单的解决方案（无需在目标位置和发射功率/信号域上进行网格搜索），已提出了得分检验的广义形式（简称为G‐Score检验），用于对确定性[15]和随机性[7],[23]目标辐射的非合作检测。最近，奇乌翁佐和萨尔沃·罗西[24],、朱等[25],以及王等[26]分别研究了分布式估计和检测问题中具有挑战性的乘性衰落场景。后者是对确定性和随机模型的推广，能够建模复杂的

2327‐4662c© 2021电气与电子工程师协会。个人使用允许，但重新出版/分发需要电气与电子工程师协会许可。更多信息请见https://www.ieee.org/publications/rights/index.html。

授权使用的范围限于：迈阿密大学图书馆。下载时间：2021年6月16日17:41:05协调世界时，来源：IEEEXplore。适用限制条款。

本文档由funstory.ai的开源PDF翻译库BabelDOCv0.5.10(http://yadt.io)翻译，本仓库正在积极的建设当中，欢迎star和关注。

本文的主要贡献总结如下

1) 本文聚焦于存在乘性衰落情况下，对具有空间相关发射（特征信号）的非合作目标进行分布式检测（DD）。我们的分布式检测场景包括：针对传感器‐目标距离相关的幅度衰减函数（AAF）的非合作目标检测、一位测量量化以及将含噪上报信道建模为二进制对称信道（BSCs），以模拟窄带物联网（NB‐IoT）中的正交多址接入信道[27]。该场景涵盖了以往研究中考虑的多种情形作为特例[7],[15],[23]。

2) 在设计具有良好性能的低复杂度融合规则时，我们同时考虑了原始量化（RQ）和基于平方的量化（SQ）。我们指出，当非视距分量在乘性衰落中变得重要时，常规的RQ[24],[26]并不总是最佳选择。因此，我们采用SQ来应对这一问题。该操作将复合检验从双边（关于信号）转变为单边（关于功率），且干扰参数仅存在于假设 H1[28]下。

3) 我们设计并优化：a) 基于常规量化（RQ）的广义拉奥（G‐Rao）方法和 b) 基于平方量化（SQ）的广义局部最优检测（LOD）（G‐LOD）方法，用于上述场景。所推导出的表达式显示，相较于基于相同条件的广义似然比（GLR）方法，其复杂度显著更低量化类型，从而突显其实际可应用性。此外，结果表明，SQ（针对G‐Rao）和RQ（针对G‐LOD）的优化（通过相应的量化阈值）具有传感器个体化特性（即每个阈值可独立于其他阈值进行优化），考虑了传感器‐融合中心信道状态，且不依赖于目标强度或其位置，从而允许离线计算。

4) 提出了一项全面的基于仿真的分析，以将所提出的G‐Rao和G‐LOD检验与以下方法进行比较：a) 它们的广义似然比对应方法；b) 基于全精度测量值的方法（即无量化和上报损失）。上述比较在相关的无线传感器网络参数范围内进行，例如感知信噪比（SNR）、直射分量与散射分量之比以及当前的上报信道质量。

我们注意到，当前工作扩展了我们早期的会议论文[24],，该论文仅基于G‐Rao检验对融合规则设计和量化器优化进行了初步分析。据我们所知，迄今为止，仅有上述工作研究了在乘性衰落下非合作目标的分布式检测问题在乘性衰落情况下 的研究。

本文其余部分组织如下。第二节阐述了所考虑的问题。第三节针对引入的设置开发了广义似然比和G得分检验。接着，第四节专注于量化器设计。第五节给出了数值结果和结论讨论。

符号说明

小写粗体字母表示向量，an表示向量a的第n个分量； E{·}、(·)T和u(·)分别表示期望、向量转置和单位阶跃函数；p(·)和P(·)分别表示概率密度函数（pdf）和概率质量函数（pmf）； χ2 k[resp. χ ′2k(ξ)]表示自由度为k的卡方（resp.非中心卡方）概率密度函数（resp.及其非中心参数 ξ）； N(μ, σ 2 )表示均值为 μ、方差为 σ 2的高斯概率密度函数； Q(·)[resp.pN(·)]表示标准形式下正态随机变量的互补累积分布函数（resp.概率密度函数），即N(0, 1)；符号 ∼（resp. a ∼）分别对应 “服从⋯⋯分布”（resp.“渐近服从⋯⋯分布”）。

II. 无线传感器网络模型和问题表述

我们考虑一组传感器k ∈ K {1,…,K}监控特定区域，以检验非合作目标的不存在（H0）或存在（H1），如图1所示。当目标存在（H1）时，假设其辐射一个未知确定性各向同性信号 θ，该信号在到达各个传感器之前受到路径损耗、乘性衰落和加性噪声的影响。

{H0: zk= wk
H1: zk= g(xk ,xT) hk θ+ wk
(1)

在(1)中，zk ∈ R表示第k个传感器的观测值，而wk ∼ N(0, σ 2 w , k )和hk ∼ N(μh , k , σ 2 h , k )是噪声以及乘性衰落项。1此外，xk ∈ Rd表示通过自定位过程获得的已知第k个传感器位置，而xT ∈ Rd表示未知目标位置。这两项xT和xk共同决定了通用AAFg(xT,xk)的值。实际上，本文可考虑任何形式的AAF（包含空间目标特征信号），只要融合中心处可获得g(·,·)即可。2

为简洁起见，在下文中我们使用简写符号gk g(xT,xk)。因此，基于上述假设，z k|H0 ∼ N(0, σ2 w,k) k|H1 ∼ N( kμh k θ k(θ)) σ2 eq ∈K σ2 eq k(θ)=( 2 k σ 2 h 和zg,,,,k，其中,g, k θ2+ σ2 w k) ,表示第k个等效方差。

此外，我们定义：1）目标信噪比，以及2）直接（视距，LoS）与散射（非视距，NLoS）目标功率项之间的比率，分别如下：

SNR 10 log10(θ 2(μ2 h+ σ 2 h)/σ 2 w) (2)
κ 10 log10(μ 2 h/σ 2 h). (3)

为应对物联网场景中的能量和带宽限制，第K个传感器将 zk量化为单个比特。3本文研究了两种量化策略。第一种情况考虑常规量化RQ[15],，即bk u(zk − τk)。第二种情况研究平方量化SQ，即dk u(z2k − γk)，该方法曾在 [23]和[29]中用于纯随机（即随机性）信号情况。对于 RQ，在 H1下的比特检测概率等于

βk(θ,xT) Q([τk −gkμh,k θ]/√σ 2 eq,k( θ)) (4)

而对于 H0 T)= Q(τk/√σ 2 w,k) β0 k βk(θ= 0, ， 它由,x给出。不同的是，对于SQ， H1下的比特检测概率等于

ρk(θ,xT) Q([√γk −gkμh,k θ]/√σ 2 eq,k( θ)) + Q([√γk+ gkμh,k θ]/√σ 2 eq,k( θ)) (5)

而对于H0，它是ρ0,k ρk(θ= 0,xT)= 2 Q(√γk/σ 2 w,k) 。

为了在物联网背景下建模能量受限通信，经过RQ（或SQ）后，第k个传感器的比特bk（或dk）通过建模为二进制对称信道的信道发送。因此，ˆ ˆ融合中心接收到一个噪声版本bk（或dk），其中Pe , k表示第k条链路的ˆ已知比特错误概率，即b k= ˆ (1−b k)[（或d k=(1−dk)]），其比特翻转概率为Pe , k。我们

我们假设传感器之间足够的空间分离意味着噪声和衰落项wks与hks 在统计上相互独立。2后者可以通过在初始化阶段（包括n= 1,…,N 个时隙）期间获取的某些训练数据来估计，在该初始化阶段中，一个协作的目标（其发射信号 θ [n] 和位置xT[n]在融合中心已知）在监测区域内移动，并由无线传感器网络传输的（量化）测量值被融合中心收集。一旦收集到足够数量的训练数据，即可通过标准学习技术（例如，基于核的回归）来估计AAF。

3在本研究中，我们仅关注：1）确定性量化器和2）单比特量化器。然而，所提出的融合方法（包括第四节中后续报道的量化器优化）原则上也可应用于非确定性（例如加扰）和多比特量化器的一般情况。上述有趣的推广留待未来的研究进行。

需要注意的是，所考虑的独立BSCs集合可以模拟在采用 NB‐IoT标准上行链路的WSN和物联网应用中通常使用的调制解码过程4 。事实上，尽管无线传感器网络需要为大量传感器提供连接能力，但这些传感器的数据速率要求较低。因此，低阶调制方案（例如，二进制相移键控）和单载波频分多址完全符合其需求。这种配置正是NB‐IoT上行链路的一种常见工作模式，下文将对此进行详细说明。

更具体地说，NB‐IoT的带宽为180kHz，对应一个 LTE物理资源块。此外，在单音传输中，可能的子载波间隔为3.75kHz（另一种允许的配置间隔为15kHz），总共包含48个子载波，每个子载波可在32ms的时隙内分配给不同的用户。后者构成了分配给单个用户以发送其数据的基本资源单元。因此，如果每个节点的感知占空比为 0.1s，则该系统可在给定小区内支持超过150个传感器对其相应测量值进行一位量化时的非干扰传输/接收。鉴于上述考虑，我们可以安全地假设传感器与融合中心之间的信道是正交的，类似于[2]。

为了采用紧凑表示法，我们将常规量化和平方量化情况下的接收比特分别收集为̂b[ˆb1 ··· ˆbK]T和̂d [ˆd1 ··· ˆdK]T。

基于这些假设，当采用常规量化时，在 H1条件下 ˆb k= 1的概率为 α rq k(θ, xT) (1 −Pe,k)βk(θ, xT)+ Pe,k(1 − βk(θ, xT))，而在 H0 α rq 0,k=(1 −Pe,k)β0,k+Pe,k(1−ρ0, k)。类似地，当采用平方量化ˆ时，在 H1条件下dk= 1的概率为α sqk(θ,xT) (1−Pe,k)ρk(θ,xT)+Pe,k(1−ρk(θ,xT))，而在 H0条件下该表达式等于 α sq 0,k=(1−Pe,k)ρ0,k+Pe,k(1−ρ0,k)。

假设检验的定义：注意，全精度测试问题，即假定可以获得原始测量值z1,… zK，依赖于未知的目标位置xT，该位置仅在信号存在时（signal is present）θ = θ0，其中 θ0= 0，才能在融合中心只有被观测到，即{H0,H1} →{θ= θ0, θ = θ0}。因此，基于全精度测量值的检验是一个具有干扰项（xT）的双边检验，该干扰项仅在 H1[28]下可识别。

然而，在考虑这两种量化方法时，有必要进行一些进一步的说明。在常规量化（RQ）情况下，未知的目标位置xT仅在信号存在时（signal is present）（θ = θ0，其中 θ0= 0），即{H0,H1} →{θ= θ0, θ = θ0}，才能在融合中心（FC）被观测到，因为βk(θ,xT)[，因此 α rq k(θ,xT)]依赖于 θ。因此，相应的检验再次成为一种具有干扰项（xT）的双边检验，该干扰项仅在 H1[28]下可识别。

我们指出，在所提出的融合规则设计模型中显式地包含噪声和衰落效应（即采用“解码与融合”方法[ 30 ]），尽管在可实现的性能增益方面具有前景，但这一任务颇具挑战性。这主要是由于由此产生的接收信号向量的概率密度函数表达式更为复杂，以及相应的得分/费雪信息表达式的计算困难所致。因此，上述类别的融合规则的设计将留待后续研究。

授权使用的限制：迈阿密大学图书馆。于2021年6月16日协调世界时17:41:05从IEEEXplore下载。限用条款适用。

III. 融合规则设计

首先，我们观察到接收向量b关于(θ,xT)的对数似然函数，即logP(b; θ,xT)，可以表示为显式形式[7]和[22]

K ∑ k=1{ bˆk log[α rq k(θ,xT)]+(1 − bˆk) log[1 − α rq k(θ,xT)]}. (7)

我们回顾一下，上述表达式同样适用于SQ，即使用对数似然logP(d; θ,xT)，只要我们将bk和 α rq k(θ,xT)分别替换为ˆdk和 α sq k(θ,xT)即可。现在我们介绍为获得所提出的融合规则而考虑的设计原理。

广义似然比是针对复合假设检验的最常用方法，其决策统计量基于常规量化，具有隐式表达式[22],

GLR( bˆ) 2 log ⎡⎣P(bˆ; θˆ1,̂xT) P(bˆ; θ0) ⎤⎦. (8)

在上述方程中，(θˆ1,̂xT)表示在 H1条件下的最大似然（ML）estimates，即

(θˆ1,̂xT) arg max (θ,xT) P(bˆ; θ,xT). (9)

类似地，基于SQ的广义似然比统计量由下式给出

GLR( dˆ) 2 log ⎡ ⎣P(dˆ; Pˆθ 1 ,̂xT) P(dˆ; Pθ 0) ⎤ ⎦. (10)

类似地，(ˆPθ 1,̂xT)表示在 H1下获得的ML估计值

(Pˆθ 1 ,̂xT) arg max ( P θ ) P(dˆ; Pθ ,xT) . (11)

我们观察到GLR[见(8)和(10)]需要求解一个优化任务。不幸的是，最大似然估计对(θˆ1,̂xT)[（分别地(ˆPθ1,̂x T)]）无法获得闭式解，这阻碍了其实际实现。因此，通常在(θ,xT)[（分别地(Pθ,xT)][7],[21],[22]上采用（联合）网格方法。相应地，广义似然比统计量能够提供对发射信号 θ（分别地功率Pθ）和目标位置xT的估计。

另一方面，戴维斯的工作提供了一种替代方法，能够利用所考虑的假设检验的双侧（当应用常规量化时）或单侧（当应用平方量化时）特性[28],，从而将得分检验推广到在 H1下仅观察到干扰参数这一更具挑战性的场景。事实上，得分检验依赖于 H0[20]下干扰参数的最大似然估计，而此处无法获得该估计，因为这些参数是不可观测的。

例如，参考我们的模型并考虑基于常规量化的拉奥检验设计，统计量的分子由(∂log[P(ˆb; θ,xT)]/∂θ)2|θ=θ0,xT=ˆxT,0给出，其中 ˆxT,0表示在假设 H0下目标位置的最大似然估计。然而，当假设 H0成立时，目标不存在absent，因此其位置x T无法被估计。

反之，如果xT已知，则拉奥（LOD）统计量将作为针对 θ（或分别地，Pθ）的相应双侧（或单侧）检验的合适决策统计量。然而，由于在本例中目标位置参数未知，我们得到的实际上是依赖于索引xT的函数型得分统计量。

因此，为克服这一技术难题，戴维斯提出了以函数上确界作为相关统计量，即

GRao( ̂b) max xT (∂ log[P(bˆ; θ,xT)]/∂θ) 2 ∣ ∣ ∣ ∣θ=θ0 Irq(θ0,xT) (12)

GLOD(̂d) max xT ∂ log[P(dˆ; Pθ,xT)]/∂Pθ ∣ ∣ ∣Pθ= P θ 0 √Isq(Pθ0 ,xT) (13)

其中，Irq(θ, xT) E{(∂log[P(ˆb; θ,xT)]/∂θ) 2 }表示关于 θ的b的费舍尔信息（FI），假设xT已知。类似地，I sq( θ) 2 } ˆ θ T) E{(∂[ (ˆ; θ T)]/∂ P,xlogdP,xP表示关于Pθ的d的费舍尔信息（FI），假设xT 已知。戴维斯方法的基本思想是选择一种检验，当在最可能的目标位置[（即对应于argmaxxT (·; xT)]）处计算的泛函统计量超过给定阈值 γfc时，接受该假设 H1。这种选择也可被解释为针对这些特定干扰参数的一种“类广义似然比（GLRT‐like）”思想。因此，(12)和(13)中的广义得分统计量均仅隐式估计目标位置xT。

下文中，我们将(12)和(13)中的决策统计量分别称为广义拉奥（G‐Rao）和广义LOD（G‐LOD),respectively, ，以表明在戴维斯框架[7]中使用拉奥和LOD作为内层统计量。

通过得分函数的显式形式（即 ∂log[P(b; θ,xT)/∂θ]）和费雪信息[，即Irq(θ,xT)]在θ= θ 0处的取值，得到GRao 的闭式表达式。其推导过程如下所示。

授权许可使用限制为：迈阿密大学图书馆。于2021年6月16日协调世界时17:41:05从IEEEXplore下载。适用限制。

IEEE物联网期刊，第8卷，第11期，2021年6月1日 9063

附录A和B。在前一种情况下， θ= θ0处的（xT‐条件）得分函数的最终表达式由以下给出

∂ logP(bˆ; θ,xT) ∂θ ∣∣∣∣∣∣θ=θ0 = K ∑ k=1( bˆk − α0rq,k) rkq gk (14)

其中辅助定义

rq k (1 −2Pe,k) αrq 0,k[1 − αrq 0,k] μh,k σw,k pN ⎛⎝ τk √σ 2 w,k ⎞⎠ (15)

已采用该方法。我们回顾一下，pN(·)用于表示标准形式下正态随机变量的概率密度函数。此外，我们强调，项rq k可以 通过将不依赖于xT的确定性项与以下部分分离开来，从而以紧凑的形式表示(14)中 θ= θ0处的（xT ‐条件）得分函数：1）随机贡献项[，即(ˆbk−αrq 0,k)]；以及2）依赖于xT的确 定性项（即gk）。在后一种情况下，xT‐条件费雪信息在 θ0处给出为

Irq(θ0,xT)= K ∑ k=1 αrq 0,k(1 − αrq 0,k)(rq k)2 g2k = K ∑ k=1 ψ rq 0,k g 2 k (16)

其中最后一行使用了定义ψ rq 0,k α rq 0, k(1 − α rq 0, k)( rq k )2。因此，广义拉奥统计量的显式形式可重写为GRao( ̂ b) ̂maxxTRao(b,xT)，其中

Rao( ̂b,xT)={∑ K k=1 ν rq k(̂bk) g(xT,xk)} 2 ∑ K k=1ψ rq 0,k g 2(xT,xk) (17)

表示在假设xT已知情况下的拉奥统计量，且我们定义了 ν rq k (̂bk) (̂bk − α rq 0,k) rq k。

相比之下，GLOD的显式表达式是通过得分函数 ̂ (log[P(d;Pθ,xT)]/∂Pθ)和费雪信息(Isq(Pθ,xT))的显式形式得出的，二者均在Pθ= Pθ0处求值。它们的推导分别在附录A和B中给出。在前一种情况下，在Pθ= Pθ 0处的（xT‐条 件）得分函数的最终表达式为

∂ logP(dˆ; θ,xT) ∂Pθ ∣ ∣ ∣ ∣ ∣ ∣P θ =Pθ 0 = K ∑ k=1 (dˆk − α sq 0,k) sq k g 2 k (18)

其中定义

sq k (1 −2Pe,k)√ γk(μ 2 h,k + σ 2 h,k) α sq 0,k[ 1 − α sq 0,k] σ 3 w,k pN ⎛ ⎝√ γk σ 2 w,k ⎞ ⎠(19) 已采用该方法。我们强调，项 s q k通过将不依赖于xT 的确定性项与随机贡献（即(dk −）分离，能够以紧凑的 形式表示(18)式中在P θ= Pθ 0处的（xT‐条件）得分函数。 α0sq ,k)]以及2)关于xT的确定性项（即，g2k）。在后一种 情况下，xT条件下的P处的费雪信息由 给出

Isq(Pθ0,xT)= K ∑ k=1 α0sq,k(1 − α0sq,k)(ksq)2 g4k = K ∑ k=1 ψ sq 0,k g 4 k (20)

其中，最后一行使用了定义ψ sq 0 ,k αsq 0, k(1 − αsq 0, k )(sq k)2。因此，G‐LOD统计量的显式形式可表示为 GLOD(̂d) ̂maxxTLOD(d,xT)其中

LOD(̂d,xT)= ∑K k=1 ν sq k(̂dk) g2(xT,xk) √∑K k=1ψ sq 0,k g 4(xT,xk) (21)

表示假设xT已知时的LOD统计量，并且我们定义了 νsq k(̂d k) (̂dk − αsq 0,k) sq k。

G‐Rao和G‐LOD统计量的吸引力源于ˆ其更简单的实现方式（因为不需要 θ1和P θˆ1），仅需对xT进行网格化即可

GRao( ̂b) ≈ max i=1,…NxT Rao( ̂b,xT[i]) (22) GLOD(̂ d) ≈ max i=1,…NxT LOD(̂d,xT[i]). (23)

因此，它们的复杂度为 O(K NxT)，相对于GLR具有显著降低。事实上，当采用RQ和SQ时，后者的复杂度分别为 O(KNxTNθ)和 O(KNxTNPθ) 。在上述表达式中，NxT和 Nθ（分别地，NPθ）表示所使用的位置和幅度（分别地， 功率）量化级数。表I总结了上述融合规则在实现中涉及 的复杂度比较。

显然， GRao τ [τ1 ··· τK] T τk ν rq (̂k) ψ rq 0 ∈ K 通过项k b 和,k，k依赖于（记为），这些项可通过优化以提升性能，如[24]中 所述。同样的推理适用于 GLOD，因为它是 γk（记为 γ [γ1 ··· γK] T）的函数，通过 ν sq k( ̂dk)和 ψ sq 0 ,k，k ∈ K实现， 这些项同样可以被优化。我们注意到，相同的优化也适用于RQ和 SQ情况下的GLR 。我们将在下文中实现这一目标。

IV. 量化器阈值的优化

我们指出，由于基于戴维斯方法[28]的检验不存在闭 式性能表达式，因此无法获得（渐近）最优的确定性量化 器。因此，[16],[29],和[31]中的原理无法应用于我们 的情况。由于这一原因，我们采用了一种改进的方法（该 方法基于一种启发式但直观的基础），该方法已成功应用 于仅具有确定性或随机目标发射的特殊情况下的分布式检 测问题[15],[23]。

具体而言，众所周知，在渐近、弱信号假设下，x T ‐完全感 知拉奥统计量Rao 服从分布

授权许可使用仅限于：迈阿密大学图书馆。于2021年6月16日17:41:05协调世界时从IEEEXplore下载。适用限制。

IEEE物联网期刊，第8卷，第11期，2021年6月1日 9064

表I 本文考虑的融合规则汇总。对于每种融合规则，还报告了通过网格离散化实现所需的计算复杂度（最后一列）

假设)5为[20] Rao(xT, τ) a ∼{χ2 1, under H0 1′2(λQ(xT, τ)), under H1. (24)

类似的结果也适用于xT‐理想观测LOD统计量LOD，该统 计量在拉奥检验的相同条件下渐近服从[20]分布

LOD(xT, γ) a ∼{N(0, 1), under H0 N(δQ(xT, γ), 1), under H1. (25)

非中心性 λQ(xT, τ) (θ1 − θ0) 2I(θ0,xT)以及偏转度 δQ(xT, γ) (Pθ1 −Pθ0)√ I(Pθ0,xT, γ)度量 6在(24)和(25)中分别给出为

λQ(xT, τ)= θ 2 1 K ∑ k=1 ψ rq 0,k( τk)g 2 (xT,xk) (26)

δQ(xT, γ)= Pθ1 √ √ √ √ K ∑ k=1 ψ sq 0,k( γk)g 4(xT,xk). (27)

此外，它们分别表示为(xT, τ和(xT, γ)的函数，以强调其 对未知位置xT以及待优化变量向量（τ或 γ）的依赖性。

最后，项 θ1和Pθ 1分别表示在 H1下的目标信号真值和功 率真值。

显然， λ Q(xT, τ)和 δ Q(xT, γ)越大，当待检测目标 位于xT时，相应的先验已知拉奥检验和LOD检验的性能 就越好。对于任一由量化器产生的数据上的先验已知广义 似然比检验同样适用。因此，我们的目标是分别设计阈值 向量 τ 和 γ，

τ arg max τ λ Q(xT, τ) (28)

5即， |θ1 − θ 0 | = c/√传感器数量K对于某个值c> 0 [ 20 ] 。 我们采用稍作修改的符号说明I ( θ, xT τ )和 ψ rq0,k( τk)[（相应地，I ( P θ , xT γ )和 ψ sq0,k( γk)]），而非I ( θ, xT)和 ψ rq0,k [ （相应地，I ( P θ ,xT) 和 ψ sq0,k ] ,），以强调其对阈值τk的依赖性。（相应地，γk的依赖性。）

γ arg max γ δQ(xT, γ). (29)

然而，通过这样做，我们可能会得到（不切实际的）解 τ 和 γ ，它们依赖于xT。幸运的是，对于这一特定问题， 优化简化为K个解耦的阈值设计（因此，优化复杂度与传 感器数量K呈线性关系），其解也独立于xT[参见(26)和 (27事)]实。上，对于广义拉奥情况，以下成立（对每个k）

max τk ⎧⎪⎨⎪⎩ψ rq 0,k( τk)= μ2 h,k σ 2 w,k pN2(τk/√σ 2 w,k) k+ β0,k(τk)[1 − β0,k(τk)] ⎫⎪⎬⎪⎭ (30)

其中k [Pe,k(1−Pe,k)]/(1−2Pe,k) 2。上述目标函数在图 2(a)中针对不同取值的Pe,k和κ进行了展示。根据量化估计 文献[32],[33]可知，对于高斯概率密度函数 τ k ，当 k= 0时（对应于Pe,k= 0），argmaxτ k ψ rq 0,k( τk)= 0成 立。然而，不难证明7，该结果对任意k = 0值均成立， 这对应于噪声上报信道（Pe,k = 0）的不同条件。值得注 意的是，(30)式中的目标函数最大化值与纯确定性（视距） 参数情况下的结果一致，因此独立于具体的视距/非视距 相对权重。

7确实，不等式p 2 N(τ ◦ k)/{k+ Q(τ ◦ k )[1 − Q(τ ◦ k )]} ≤ p 2 N(0)/{k+ Q(0)[1 − Q(0)]}，其中 τ ◦ k τ k /√σ 2 w , k，可以重写为 {p 2 N(τ ◦ k)Q(0)[1 − Q(0)] −p 2 N(0)Q( τ ◦ k )[1 − Q(τ ◦ k)]} + k{p 2 N(τ ◦ k) −p 2 N(0)}≤ 0. 上述条件始终满足，因为花括号内第一项的负性直接来源于理想二进制对称信道的结 果（ k = 0 [ 32 ] , [ 34 ] , 1 > 0 2 { 2 N( τ ◦ ) − ）， 而对于第二项， ( ) k 和 ( ) p k p 2 N( 0 )} ≤ 0 均成立（因为正态分布在零处达到其众数）。

授权许可使用仅限于：迈阿密大学图书馆。下载时间：2021年6月16日17:41:05协调世界时，来源：IEEEXplore。适用限制条款。

丘翁佐等：乘性衰落下无线传感器网络中的分布式检测 9065

常规量化（RQ）(ψrq0,k(τk))和(b)平方量化（SQ）(ψsq0,k(ρ0,k))的阈值目标，对应Pe,k∈{0, 0.1, 0.2}和 κ ∈{−5, 0}dB。)

(a)G‐Raorq和GLRrq中选择 τk 的目标函数。(b)G‐LODsq和GLRsq中选择ρ 0,k（即， γ k）的目标函数。

不同的是，对于G‐LOD情况，我们有（对每个传感器数量K）

max γk ⎧⎪⎨⎪⎩ψ sq 0,k(γk)=(μ2 h,k+ σ 2 h,k) 2 (σ 2 w,k) 2 × pN2(√γk/σ 2 w,k)(γk/σ 2 w,k) k+ ρ0,k(γk)[1 − ρ0,k(γk)] ⎫⎪⎬⎪⎭. (31)

这种最大化可以基于传感器的虚警概率ρ0,k（与 γk)存在 一一对应关系）来重新表述

ψ sq 0,k( ρ0,k)= (μ2 h,k+ σ 2 h,k) 2 (σ 2 w,k) 2 × pN2(Q−1(ρ0,k/2))[Q−1(ρ0,k/2)] 2 k+ ρ0,k(1 − ρ0,k) . (32)

上述目标在图2(b)中针对不同的Pe,k和 κ值进行了展示。 优化的ρ 0,k可通过一维线搜索轻松计算得出。值得注意的 是，式(32)中的目标最大化器与纯随机（NLoS）参数在 [23],情况下的结果一致，因此独立于特定的视距/非视距 相对权重。

备注：尽管原始和平方量化器阈值的优化已被证明独 立于具体的视距/非视距相对权重，但我们强调，在这两 种情况下，检测性能将显著依赖于上述参数。事实上，我 们观察到（经过优化的）非中心性 λ Q(xT, τ)通过项 ψ rq 0, k(τk),k= 1,...K而增长，其中μ 2 h,k / σ 2 w,k[见公式 (30)]。相反地，（经过优化的）非中心性δ Q(xT, γ)通过项 ψ sq 0,k(ρ0,k),k= 1,...K而增长，其中(μ 2 h,k + σ 2 h,k )/ σ 2 w, k / σ 2 w[见公式(32)]。因此，上述观察表明：1)G‐LOD的性 能在广泛的视距/非视距相对条件下可能仅有微弱依赖 （由于存在和μ 2 h,k+ σ 2 h,k）；2)当非视距项占主导时， G‐Rao预计将遭受严重的性能下降（由于缺少σ 2 h,k）； 3)在高度视距条件下，由于公式(32)中(μ 2 h,k + σ 2 h,k )/ σ 2 w,k 的平方作用，我们预计G‐Rao在低信噪比下将获得更显 著的增益。

V. 数值结果与讨论

仿真设置：在此，我们比较基于第四节中提出的阈值 优化设计的优化G‐Rao、G‐LOD和GLR检验的数值性能。 具体而言，我们的仿真设置考虑一个二维（xT ∈ R 2）正 方形区域，定义为 A [0, 1]2,，其中由具有K= 49个传 感器的无线传感器网络检测非协作目标。为简化起见，节 点以网格方式均匀覆盖整个 A。关于感知模型，所考虑 的AAF为幂律，即

g(xT,xk) 1/ √1+(‖xT −xk‖/ η)α (33) 其中我们设定了 η= 0.2（即目标尺寸近似值）和 α= 4 （即衰减指数）。此外，为简化起见，wk ∼N(0, σ 2 w= 1)和 μ2 h= 1，k ∈ K。最初，我们假设二进制对称信道无误差， 即Pe,k= 0，k ∈ K。所有仿真均基于 105次蒙特卡洛运行。

根据第三节，GLR、GRao和GLOD的实现利用了网 格搜索。具体而言，目标信号 θ（或功率Pθ）的搜索空间 被假定为Sθ [−θ¯, θ¯]（或SPθ [0, Pθ¯]），其中 θ¯> 0 （或Pθ¯ > 0）满足信噪比= 20 dB。然后将网格上各点组 成的向量定义为[−g T θ 0 gθT] T（或[0 gPTθ] ），其中gθ（或 gPθ）收集对应于信噪比值 −10:2.5:20(dB)的目标强度 （或功率值）。因此，幅度和功率区间的数量分别等于 Nθ= 25和NP θ = 13。其次，xT的搜索范围与监测区域 （SxT= A）一致。相应地，二维网格是通过对 A以N x T=N 2 c个点进行均匀采样的结果，其中Nc= 100。在此 设置下，G‐Rao（G‐LOD）的评估需要N2 c= 104个网格点， 而GLR则需要N2 cNθ= 2.5×105（或N2 cNP θ = 1.3×105） 个点。这使得G‐Rao（G‐LOD）相对于基于相同量化策略 的GLR，复杂度降低了> 20（或> 10）倍。

考虑的基线：为了进行全面比较并评估量化损失，我 们考虑以下基线：1）基于全精度测量值zk的广义似然比； 2）G‐Rao；以及3）基于相同数据的G‐LOD检验。关于 第1）项，其（隐式）表达式类似于(8)中的表达式，并通 过以下方式实现

授权许可使用仅限于：迈阿密大学图书馆。于2021年6月16日17:41:05协调世界时从IEEEXplore下载。适用限制。

IEEE物联网期刊，第8卷，第11期，2021年6月1日 9066

考虑一个具有K= 49个传感器且目标信噪比为= 10分贝的无线传感器网 络。常规量化和平方量化的传感器阈值根据第四节中报告的设计进行设置。

如下显式表达式：

fp GLR(z)= max (xT,θ) K ∑ k=1{ log[σ 2 w,k/ σ 2 2 w,k] −[(zk −gkμh,k θ)2/ σ 2 eq,k(θ)]}. (34)

对于2)和3)，它们的显式表达式（为简洁起见，证明未包含 在内）分别为

fp GRao(z) max xT (∑K k=1 gkμh,k zk/σ 2 w,k) 2 ∑K k=1 g 2 kμ 2 h,k / σ 2 w,k (35)

fp GLOD(z) max xT ∑K k=1 1 2[ g 2 k σ 2 μ2 h,k+ σ 2 h,k)( z2k σ 2 w,k −1)] √1 2∑ K k=1 g 4 k σ 4 μ2 h,k+ σ 2 h,k) 2 . (36)

我们注意到，为了应用G‐LOD，实际上是从平方值z2k开 始进行推导的（这会导致检验的性质从双侧变为单侧，类 似于一位量化情况下的变化）。

结果讨论：首先，图3D给出了在固定PF= 0.01条件下，所考虑的融合规则相对于 κ(dB）的比较，以评估它 们在非合作目标发射的视距/非视距相对项比值下的检测 灵敏度。在当前分析中，目标位置xT在每次运行时（当 H1被抽取时）在 A内随机采样。我们假设目标的感知信 噪比为= 10 dB。结果表明，在整个 κ范围内，G‐LOD sq的性能与广义似然比sq相当，并且优于基于常规量化的 G‐Rao和广义似然比。对基于全精度的检验性能观察表明： 1）量化损失；2）在乘性衰落下使用拉奥检验存在的问题， 尤其是在低 κ条件下。

然后，在图4中，我们在约束条件PD下对所考虑的融 合规则与信噪比(dB）进行比较（受限于PF= 0.01）， 以评估它们在两种不同散射程度条件下（即 κ= 0dB和

κ= 10分贝。(b) κ= 0分贝。)

κ= 10分贝。结果突显了广义似然比（GLR）与基于相同 类型数据（即固定阈值、常规量化或平方量化）的相应广义 得分检验（G‐Rao或G‐LOD）之间具有高度一致性。通过 比较G‐Raorq 和G‐LODsq，可以明显看出它们的相对性能 取决于散射程度条件。例如，在高视距条件下，G‐Raorq表 现更优；而在低视距条件下，G‐LODsq的优势则更加明显。 此外，从G‐LODfp 相对于GLRsq 和G‐Raofp实现的性能差 距缩小来看，平方操作的优势也十分显著。

作为补充分析，在图5中，我们通过分析可变数量的传 感器K来深化PD比较（受限于PF= 0.01）。具体而言，我

们考虑相同的方形监控区域 A=[0, 1] 2，但假设网格长度上 的传感器数量线性增加（即K的二次增长），以研究无线传 感器网络网格密集化对系统检测率的影响。正如预期的那样，

授权许可使用仅限于：迈阿密大学图书馆。于2021年6月16日17:41:05协调世界时从IEEEXplore下载。适用限制。

丘翁佐et al.：乘性衰落下无线传感器网络中的分布式检测 9067

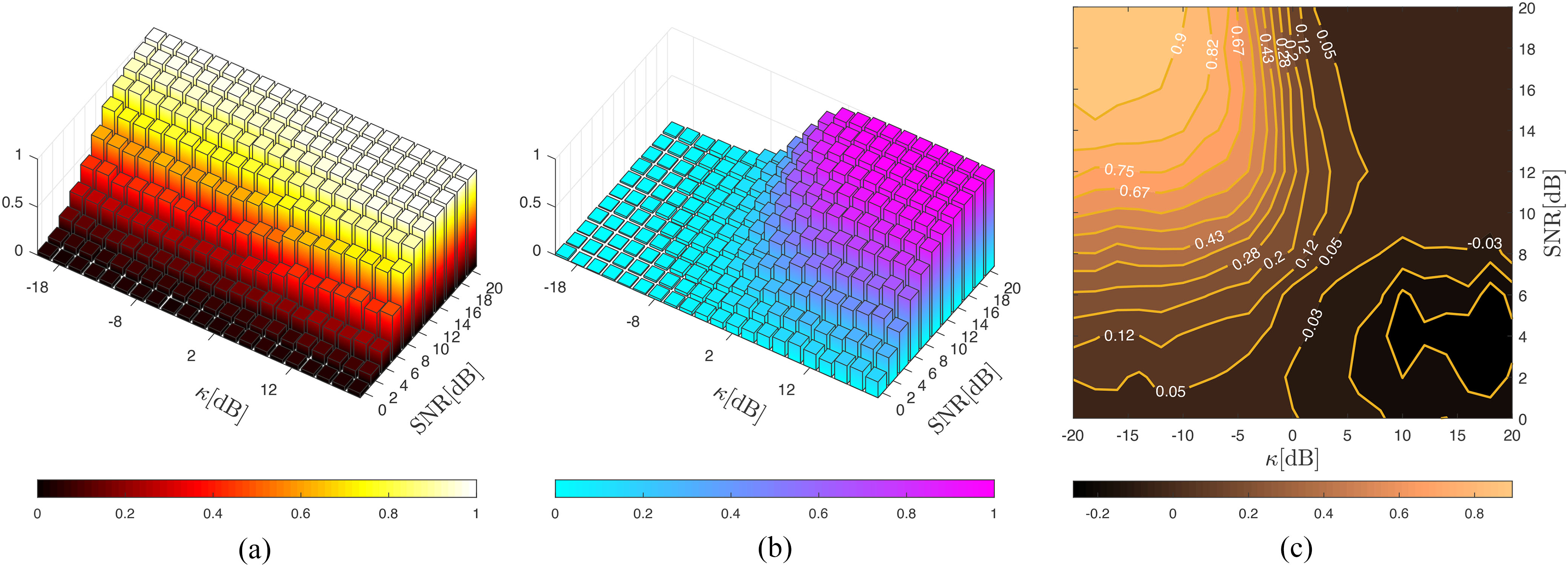
(分贝)的变化曲线，融合中心虚警概率设为PF= 0.01，其中(a)为G‐LODsq，(b)为 G‐Raorq，(c)为其差值 PD (PGLODD−PGRaoD)。考虑一个具有K= 49个传感器的无线传感器网络：其阈值按第四节中的方法进行优化；假设信道为理 想二进制对称信道，即Pe,k= 0。)

κ ∈ 0分贝。(b) κ ∈ 5分贝。)

所有考虑的融合规则都受益于更精细的传感器网格对目标 的监测，其中基于FP的规则在较少数量的传感器（即更 粗糙的网格）下即可实现接近理想性能的表现。不同的是， 关于基于一位量化的融合规则，SQ‐based规则在较小的 K值下表现出略微提升的性能。然而，随着无线传感器网 络密集化程度的增加，这种相对于RQ‐based规则的优势 逐渐减小。例如，在目标为PD ≈ 0.8（或PD ≈ 0.9）时， 对于RQ‐based和SQ‐basd规则而言，分别只需一个包含 K= 49（或K= 64)个传感器的均匀网格即可。

在 κ和信噪比维度上，G‐LODsq与G‐Raorq的更深 入比较如图6所示。具体而言，我们展示了融合中心虚警 概率设为PF= 0.01时，G‐LODsq（左）和G‐Raorq （中）的PD随(κ,信噪比)(dB)的变化情况，以及它们的 差值 PD（右）。通过分析结果可以看出，G‐Raorq对 κ 的低值（非视距条件）非常敏感。相反，G‐LODsq几乎不 受特定的视距/非视距条件（即 κ的值）的影响。两种融合 规则的性能均随信噪比降低而下降。通过比较整个(κ,信 噪比)平面上两种规则的性能差异PD (PGLODD− PGRao D)]，可以明显看出高信噪比和高 κ是G‐LODsq “获 胜”的区域，而在低信噪比和低 κ的情况下则出现相反的 结果（即G‐Raorq获胜）。然而，在后一种情况下， G‐Raorq相对于G‐LODsq （右图）所带来的性能增益，不 如G‐LODsq获胜区域的增益显著。这些结果可以通过查 看第IV节末尾强调的项ψ rq 0,k(τk)和ψ sq 0,k(ρ0,k)[（分别 见式(30)和式(32)）],及其相对趋势来解释。实际上， ψ rq 0,k(τk)和ψ sq 0,k(ρ0,k)直接影响xT‐理想非中心性参数 λQ(xT, τ)和 δQ(xT, γ)的值，从而（从上方）限制了 G‐Raorq和G‐LODsq的可达性能。

然后，我们通过图7深入分析报告错误的影响。后者在 PF= 0.01条件下提供了七种融合规则相对于Pe,k= Pe和k ∈ K（即所有传感器具有相同的比特错误率）的PD比较。 考虑了两种不同的散射程度情况，分别为 κ= 0dB[图7(a)] 和 κ= 5 dB[图7(b)]。结果表明，比特错误率（即Pe）的 增加对所有基于RQ/SQ的规则产生不利影响，并进一步扩大 了它们与基于FP的规则之间的差距。值得注意的是，在 κ= 5 dB的情况下，当P e ≈ 0.15时，SQ相对于RQ的优势几 乎消失。

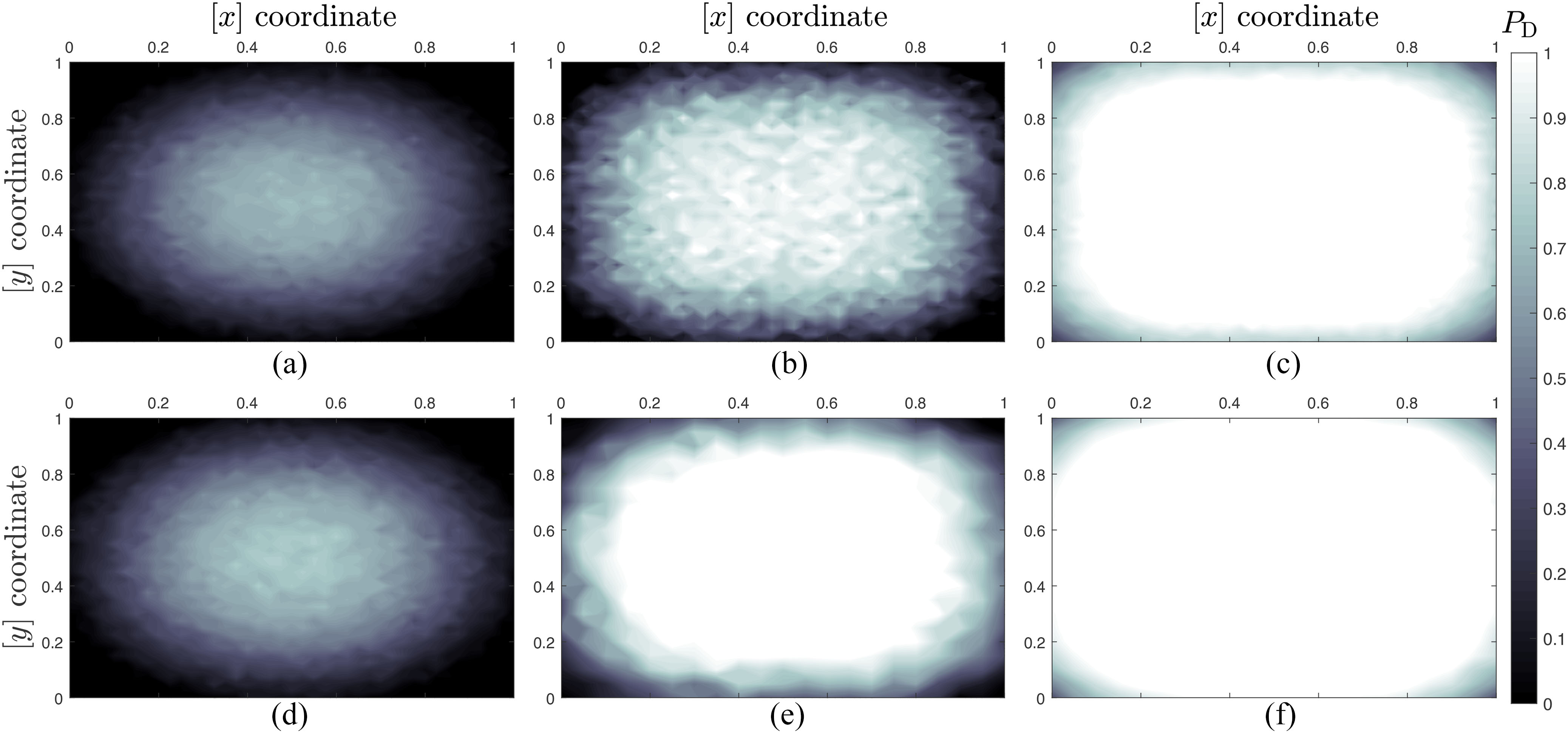
最后，我们研究了所考虑的融合规则在整个监视区域内的检测 覆盖范围特性

授权许可使用限制：迈阿密大学图书馆。于2021年6月16日17:41:05协调世界时从IEEEXplore下载。适用限制条款。

9068 IEEE物联网期刊，第8卷，第11期，2021年6月1日

和(f)，分别对应GLRfp和G‐LODfp]。融合中心虚警概率设为PF= 0.01。考虑包含K= 49 个传感器的无线传感器网络，目标的感知信噪比分别为= 5 dB和 κ= 0dB。相应的决策通过误码率为Pe,k= 0.1的二进制对称信道传输。常规量化和平方量化的传感器阈值根据第四节中所述的设计方法设定。)

A。为此，在图8中，我们报告了在PD （在PF= 0.01下） 随目标位置xT的变化情况（信噪比分别为= 5 dB和 κ= 0 dB），针对所有考虑的检验方法，但G‐Raofp除外， 因其在此特殊的非视距配置中性能较差。显然，从定性角 度来看，所有检验方法的PD(xT)曲面相似。此外，它突 显了在监视区域边缘处检测性能较低的问题。这一结果源 于所分析场景中 A内的规则无线传感器网络部署。通过 不同检验方法之间的比较可以看出，G‐LODsq检验相对 于GLRsq仅有微小损失，而相对于G‐Raorq和GLRrq则具 有显著增益。显然，由于稀疏（一位）量化的退化效应， 其检测覆盖范围不如所考虑的全精度对应方法。

VI. 结论与未来方向

在本研究中，我们设计了一种基于无线传感器网络的 分布式检测方案，该方案考虑了以下因素：1）乘性衰落； 2）量化测量；3）非理想且非相同的二进制对称信道。待 检测的目标发射一个未知的（因其为非合作的）确定性信 号（θ），其位置未知（xT）。由于xT仅为在 H1下存在 （即当θ = 0时）的干扰参数，我们设计了Rao和LOD检 验的广义形式，作为对GLR[的有吸引力的低复杂度替代 方案，后者需要在整个空间(θ,xT)]上基于相同的量化选 择进行网格搜索。这些广义形式源自[28]中的框架。所得 到的G‐Rao和G‐LOD形式仅需对一组假设xT已知条件下 获得的xT‐条件决策统计量关于xT进行单次最大化，从而 避免了在 θ （或P θ)）上进行网格搜索的需求。此外，我 们提出了一种有效准则（来源于半理论性能） 针对任一种量化类型（RQ或SQ）优化传感器阈值。这导致 RQ选择零阈值，而SQ则进行简单的1维搜索。此外，这些结 果被证明与特定的 κ值无关。G‐LODsq的数值结果强调了以 下几点：1）在视距（LoS）情况下，PD值与G‐Raorq和 GLRrq相近；2）在非视距（NLoS）情况下，GLRsq具有相 似的性能；3）在相关 κ范围内，相对于G‐Raorq具有显著增 益。因此，我们认为，在广泛的视距/非视距条件下，采用 SQ结合G‐LODsq是此类场景下分布式检测的一种颇具吸引 力的设计选择。唯一的例外是高视距低信噪比场景，此时在 融合中心应优先联合使用RQ和G‐Rao检验。

未来研究方向将研究在更具挑战性且更接近实际场 景中通过传感器融合实现的分布式检测。这些场景包括多 比特量化器[35],对物理层攻击的鲁棒性[36],时间相关报 告信道[37],多维测量模型[38],噪声和模型概率密度函数 未完全指定的情况（例如，未知AAF）、具有稀疏性的模 型[8],以及能量高效删减传感器。此外，推导广义得分检 验的检测概率（PD）和虚警概率（PF）的（渐近）理论 表达式也被视为未来研究的一个（具有挑战性的）方向。