求解分配问题(二) 二分图最大匹配算法

我的前一篇文章介绍了对于分配问题的Kuhn-Munkre算法，该算法其实可以看作是邻接矩阵形式的匈牙利算法，如果更抽象地看这个算法，它可以看成是一个二分图匹配算法的变体算法，具体的说，是二分图最大权重匹配算法。我打算也把二分图最大权重匹配算法也介绍下，不过最大权重匹配算法又是基于最大匹配算法设计的，所以这篇文章先介绍二分图的最大匹配算法

二分图最大匹配问题

分配问题从图论的角度看其实是一个二分图(Bipartite Graph)，就是说图中有两个点集，在各自的点集内的点互相没有连接，两个点集间的点可以连接，每个点存在多个允许的连接，如下图所示：

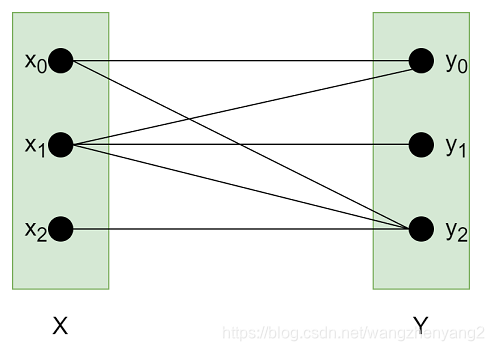
如果我们对二分图中的每个点，都确定最多只有一条连接，那么称之为该二分图的一个匹配，例如：

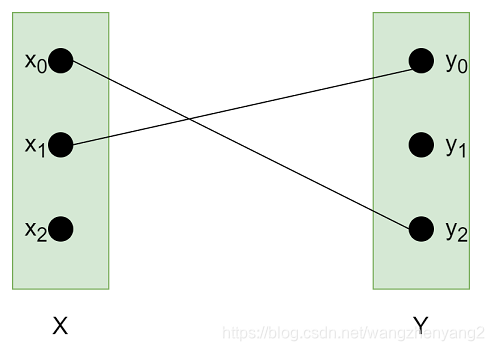
如果每个点都有一条线确定，即匹配的线数正好等于单个点集点数$n$，那么称之为完美匹配，如下图：

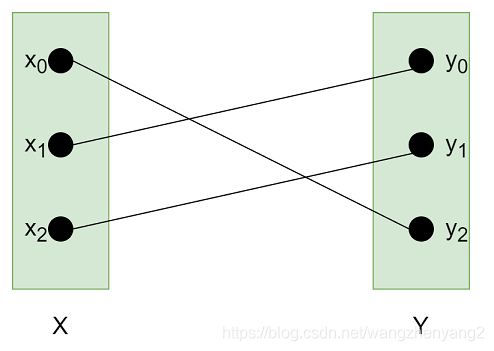
对应于现实问题，我们当然希望尽量达到完美匹配，但是因为点的可选连线情况可能导致无论如何也达不到完美匹配，所以自然而然产生了最大匹配问题(Max-Bipartite Matching)，最大可以找到多少条匹配线

用数学语言描述：

• 图$G=(V,E)$是一个二分图，$n=|V|$，$m=|E|$，$\delta (v),v\in V$表示一端连接到点$v$的所有边，xe∈{ 0,1}x_e\in \{0,1\}xe​∈{ 0,1}表示边$e$是否被选中，则有最大匹配问题：
  max∑e∈Exes.t.∑e∈δ(v)≤1,∀v∈Vxe∈{ 0,1},∀e∈E \begin{aligned} max\quad& \sum_{e\in E} x_e\\ s.t.\quad& \sum_{e\in \delta(v)}\leq 1,\forall v \in V \\ & x_e\in \{0,1\},\forall e \in E \\ \end{aligned} maxs.t.​e∈E∑​xe​e∈δ(v)∑​≤1,∀v∈Vx