题解- CF1338B Edge Weight Assignment
题目意思
- Div1 B
- 给你一个颗树让你给他上面的点填数字使得任意两个叶子之间的异或和为
0
0
0,问最多/少多少种不同的权值来使得填数字是合法的。
-
n
,
a
i
,
b
i
≤
1
0
5
n,a_i,b_i\leq 10^5
n,ai,bi≤105
S
o
l
\mathrm{Sol}
Sol
- 一道结论题
- 最小值很显然就只有
1
,
3
1,3
1,3两种情况(当存在任意两个叶子之间的距离为奇数那么是
3
3
3,因为偶数个相同的数异或为
0
0
0)这个一遍
d
f
s
dfs
dfs就可以了。
- 那么对于最大值,我们有个结论就是把一个节点的叶子节点合并成一个节点然后计算修改过后树边的数量(样例来画个图来看看
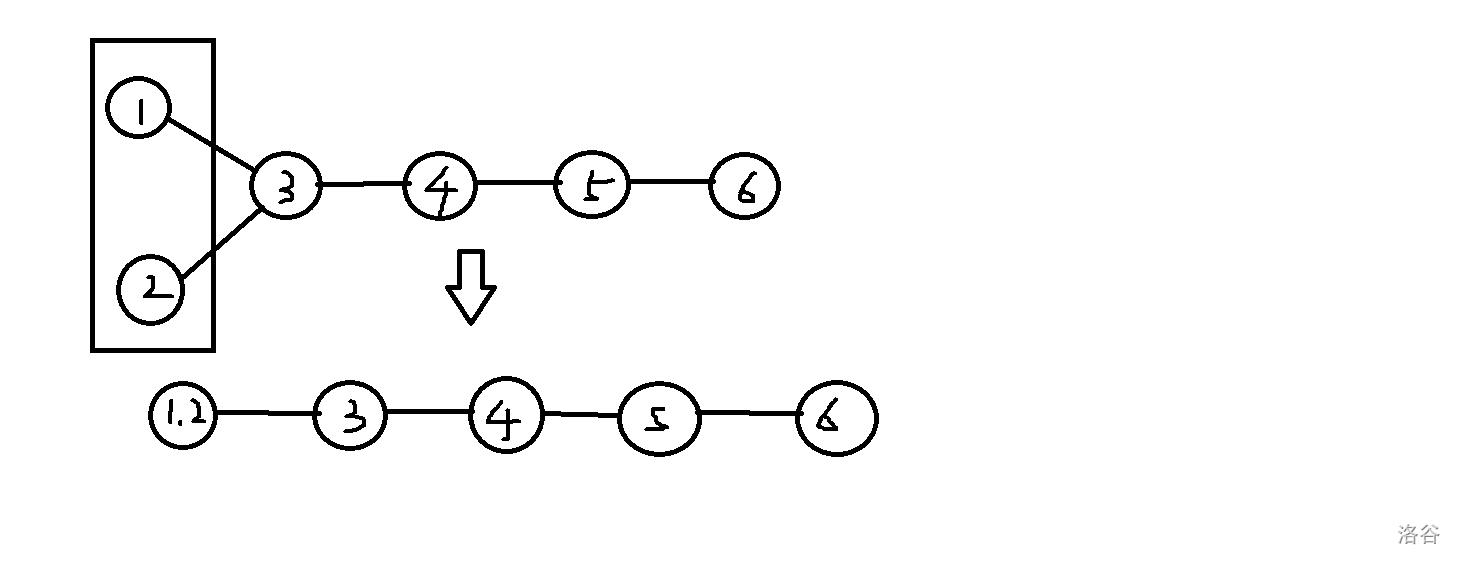
C
o
d
e
\mathrm{Code}
Code
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
inline int read()
{
int sum=0,ff=1; char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-') ff=-1;
ch=getchar();
}
while(isdigit(ch))
sum=sum*10+(ch^48),ch=getchar();
return sum*ff;
}
const int N=1e5+5;
int n,m,zz,in[N],vis[N];
vector<int> G[N];
inline void dfs(int u,int fa,int dep)
{
if(G[u].size()==1&&dep%2==1) zz=1;
for ( int i=0;i<G[u].size();i++ )
{
int v=G[u][i];
if(v==fa) continue;
dfs(v,u,dep+1);
}
}
int main()
{
n=read();
for ( int i=1;i<n;i++ )
{
int x,y;
x=read(),y=read();
G[x].pb(y);
G[y].pb(x);
in[y]++;
}
int rt=0;
for ( int i=1;i<=n;i++ ) if(G[i].size()==1)
{
rt=i;
break;
}
dfs(rt,0,0);
(zz)?printf("3 "):printf("1 ");
int mx=n-1;
for ( int i=1;i<=n;i++ )
{
int gs=0;
for ( int j=0;j<G[i].size();j++ )
{
int v=G[i][j];
if(G[v].size()==1) gs++;
}
mx-=gs;
if(gs) mx+=1;
}
printf("%d\n",mx);
}








 博客详细解析了CF1338B问题,即如何在树上为节点分配数字,使得任意两个叶子节点间的异或和为0。博主指出,最小解决方案可能是使用1或3种不同的权值。通过DFS可以确定是否存在奇数距离的叶子节点,以判断最少权值数。同时,博主提出一个结论,通过合并叶子节点可以求解最大解决方案,并保证时间复杂度为O(n)。
博客详细解析了CF1338B问题,即如何在树上为节点分配数字,使得任意两个叶子节点间的异或和为0。博主指出,最小解决方案可能是使用1或3种不同的权值。通过DFS可以确定是否存在奇数距离的叶子节点,以判断最少权值数。同时,博主提出一个结论,通过合并叶子节点可以求解最大解决方案,并保证时间复杂度为O(n)。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








