自考离散数学
1-1.命题符号化
前推后: 只要…就会…,因为…所以…,如果…就…。
后推前:只有…才…。
只有…才… = 除非…否则…同或异或
同或意思是可以同时发生,异或意思是不能同时发生
1-2.真值表
没什么记忆的
1-3.常用命题定律
- A <=> ┐┐A
- A <=> A∧A
- A <=> AvA
- A∧(BvC) <=> (A∧B) v (A∧C)
- Av(B∧C) <=> (AvB) ∧ (AvC)
- ┐(A∧B) <=> ┐A v ┐B
- ┐(A v B) <=> ┐A ∧ ┐B
- A v F <=> A
- A v T <=> T
- A ∧ F <=> F
- A ∧ T <=> A
- A ->B <=> ┐A v B
1-4.永真式永假式
真值表都为1是永真式(重言式)
真值表都为0是永假式(矛盾式)
2-1. 主范式
小项,上面不开口
大项,上面开口
主析取范式,析取连接,原子命题是合取(小项)
主合取范式,合取连接,原子命题是析取(大项)
- 真值表法
1是小项(合取) 0是大项(析取)
如题求主析取范式,主析取范式是析取连接,原子命题是合取,合取是小项,取真值表为1的。0是非的意思要加上┐,小项是合取连接,所以把三个用合取连接,再将五个小项用析取连接。
简写
小项由小写m表示,大项由大写M表示
我们发现简写后,m后面是二进制数,我们可以改成十进制,改成十进制之后,还可以进一步简写∑(1,3,5,6,7)
2-2.大小项的个数
1就是小项的个数
0就是大项的个数
重言式结果全都为1,命题的数量是2的n次方,小项的结果也都是为1的,那么小项的个数就是2的n次方
3-1.谓词公式的符号化
3-2.量词的辖域
4-1.幂集
4-2.并集
4-3.真子集
4-4.补集
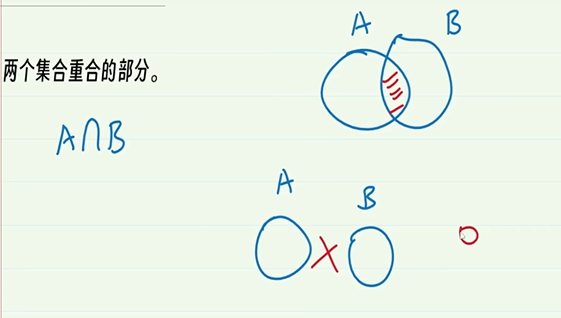
4-5.交集
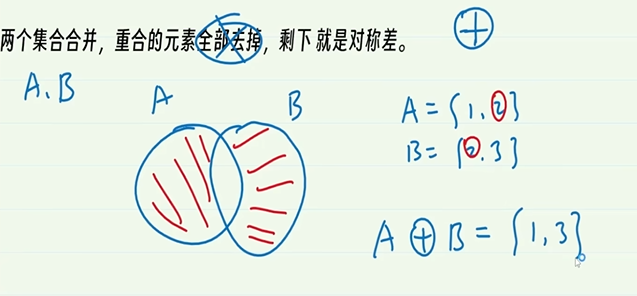
4-6.对称差
4-8.基数
基数也叫势
4-9.笛卡尔积
注意,A和B的有序对和B和A的有序对是不一样的
5-1.二元关系
如果两个元素的所有值,全都有关系,那么就是一个笛卡尔积
这个题, 要先算括号里的并交的数据,再取dom的数据
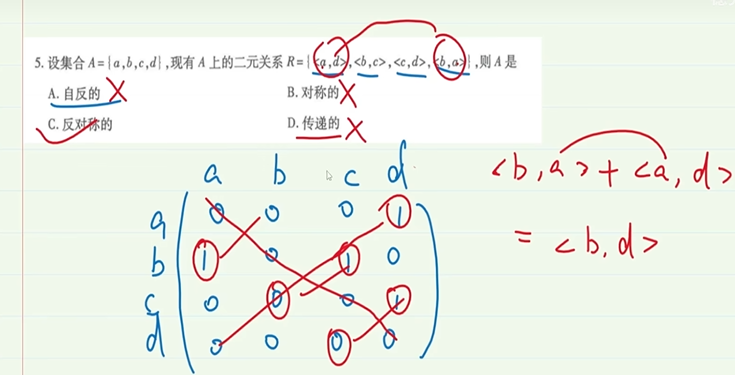
5-2.二元关系的性质
求逆关系
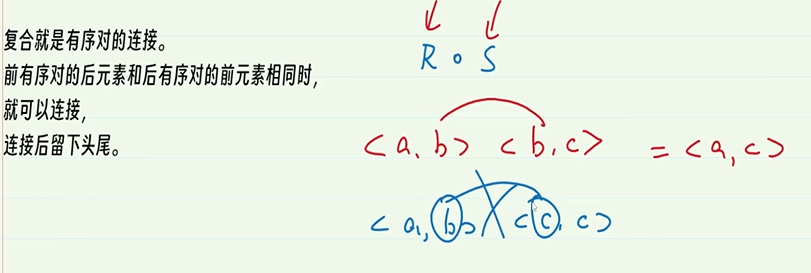
5-4.复合关系
5-6.闭包
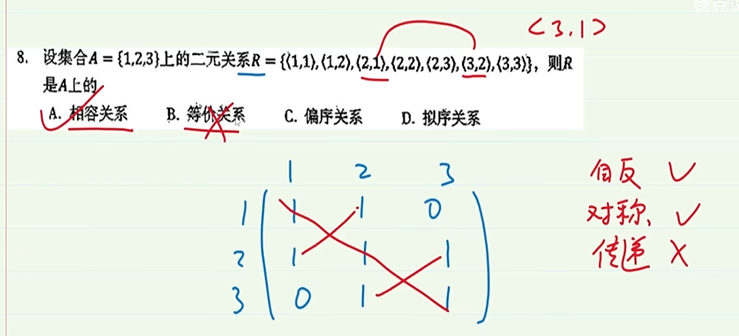
5-7.等价、相容、偏序、拟序
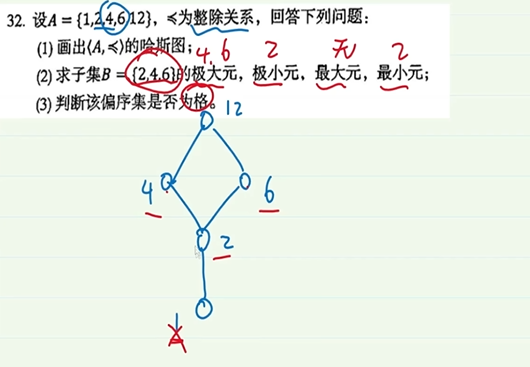
5-12.哈斯图
极大元和极小元是相对关系,最大元和最小元是绝对关系。子集2,4,6 极大元就是最上层,同一层的元素。极小元就是最下层,同一层的元素。最大元是最上层的元素,且唯一,4,6是最上层的,但是他们没有一个最大的,所以最大元为无,最小元就是2
格的意思是任意取两个点,向上向下汇聚到一个点,那么就为格
5-14.函数
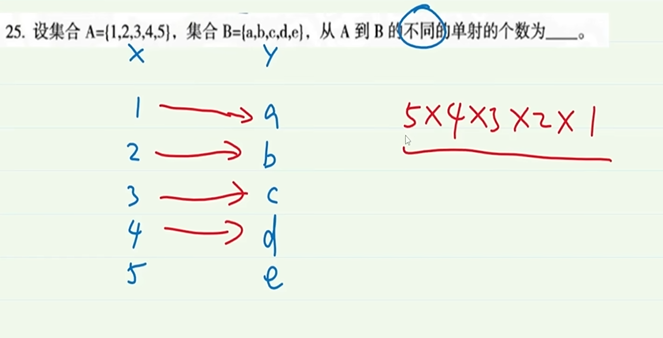
5-16.单射
5-17.满射
5-18.双射
6-1.二元运算的关系
6-2.单位元
6-3.逆元
6-4.零元


6-6.群
封闭,运算完也要在集合里
可结合,满足结合律
含单位元,有幺元
可逆,每个元素都有逆元
可交换,满足交换律
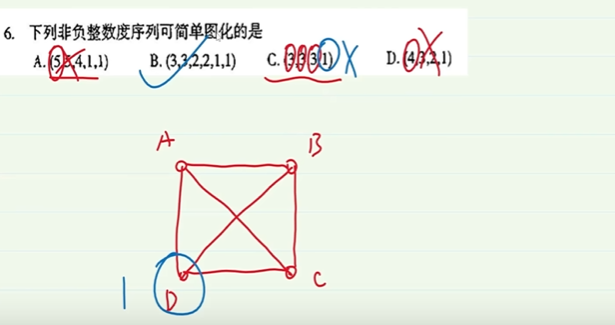
7-1.格的判断
7-2.补元
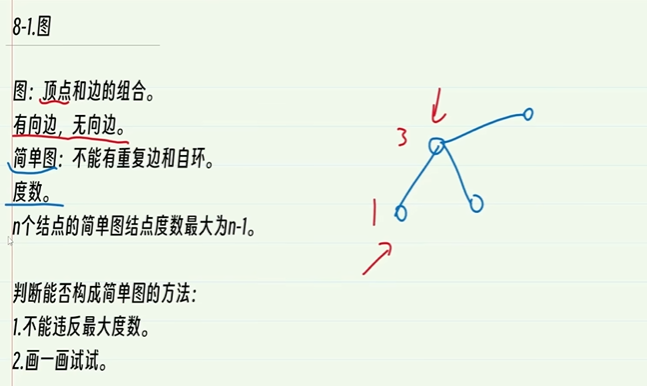
8-1.图
注意度数就是多少条边,度数的数量就是节点数-1
8-2.无向图的握手定理
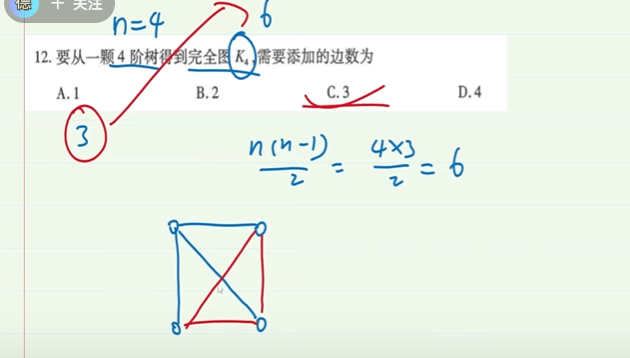
8-3.完全图
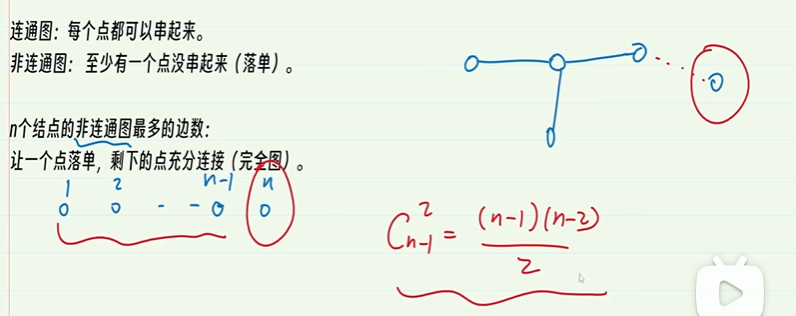
8-4非连通图最大变数
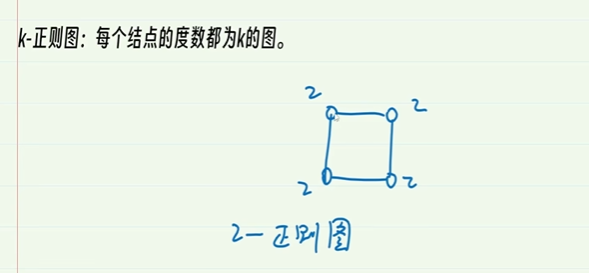
8-5.正则图
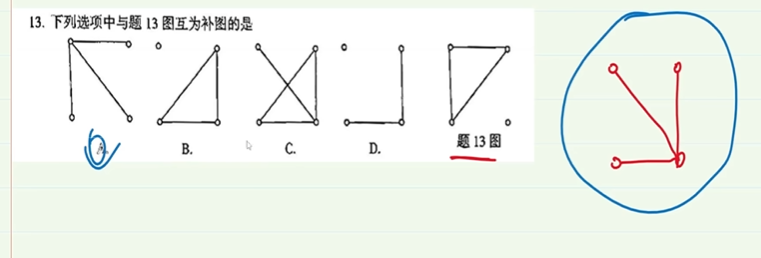
8-6.补图
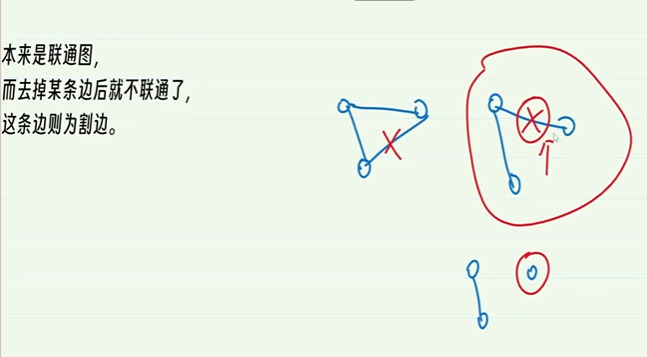
8-10.割边
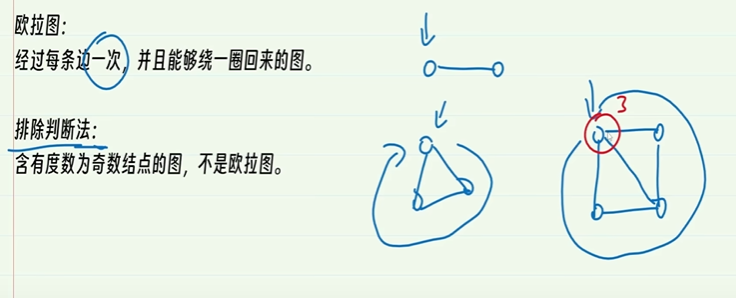
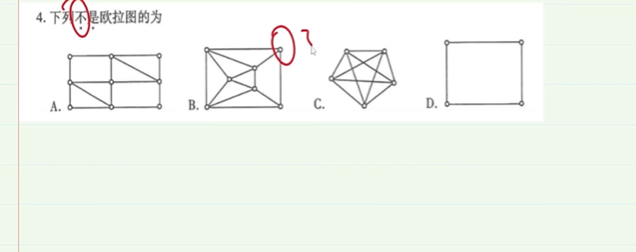
9-1.欧拉图
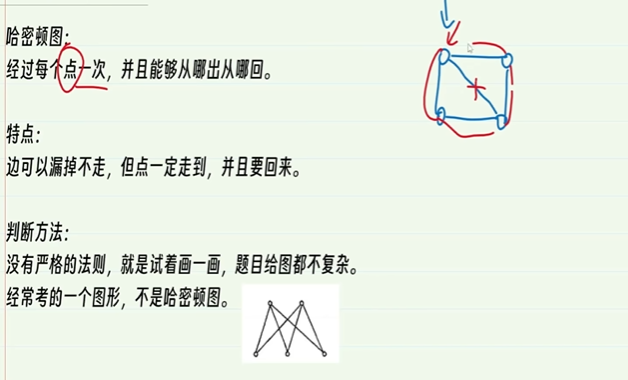
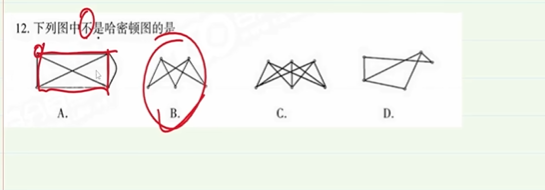
9-2.哈密顿图
9-5.欧拉公式
9-6.树
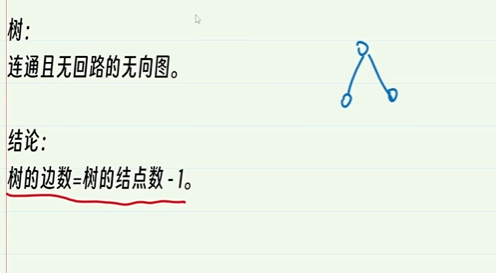
树的边数 = 树的节点数-1












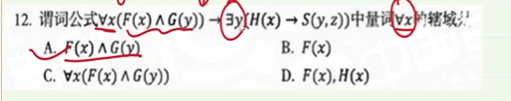



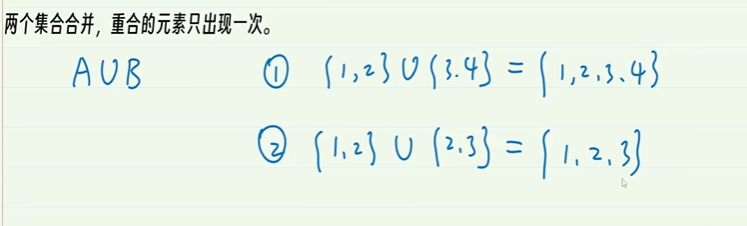




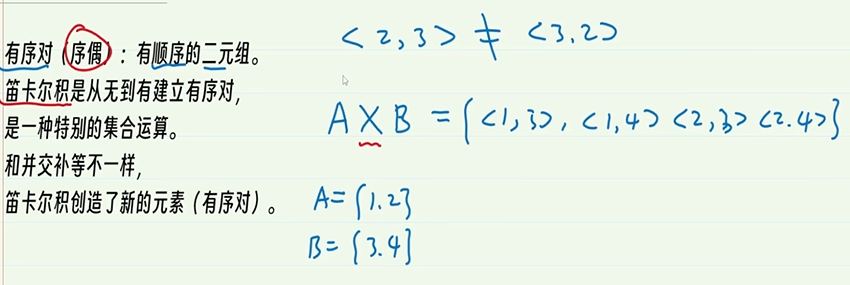



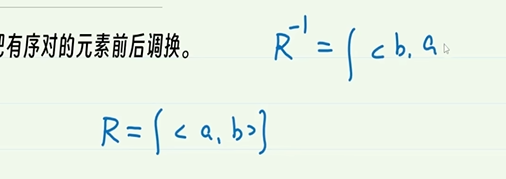





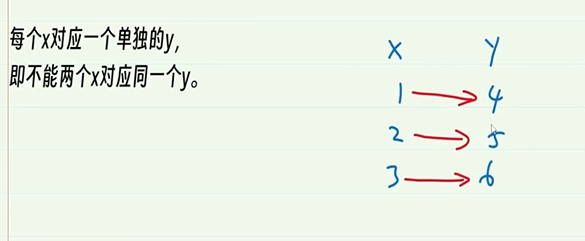




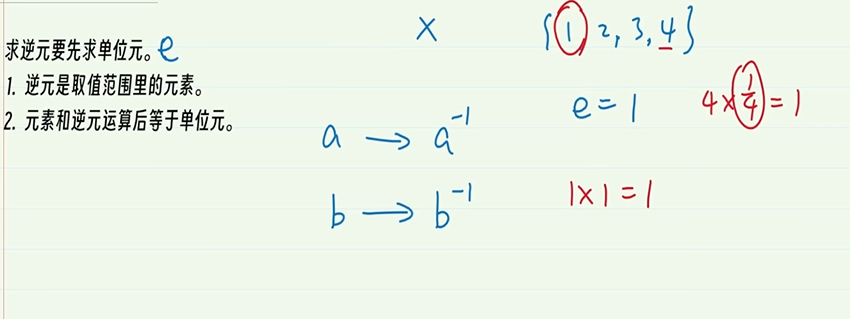













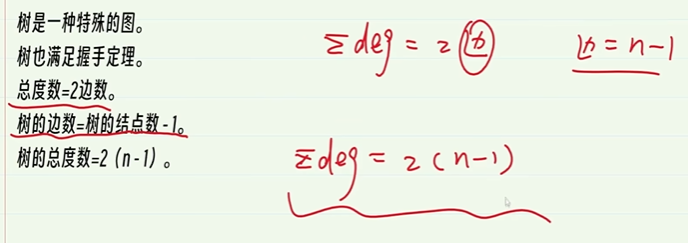

















 4584
4584

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








