Multi-Head Attention详解

文中大部分内容以及图片来自：https://medium.com/@hunter-j-phillips/multi-head-attention-7924371d477a

当使用 multi-head attention 时，通常d_key = d_value =（d_model / n_heads），其中n_heads是头的数量。研究人员称，通常使用平行注意层代替全尺寸性，因为该模型能够“关注来自不同位置的不同表示子空间的信息”。

通过线性层传递输入

计算注意力的第一步是获得Q、K和V张量;它们分别是查询张量、键张量和值张量。它们是通过采用位置编码的嵌入来计算的，它将被记为X，同时将张量传递给三个线性层，它们被记为Wq, Wk和Wv。这可以从上面的详细图像中看到。

• Q = XWq
• K = XWk
• V = XWv
  为了理解乘法是如何发生的，最好将每个组件分解成这个形状：
• X的大小为(batch_size, seq_length, d_model)。例如，一批32个序列的长度为10，嵌入为512，其形状为(32,10,512)。
• Wq，Wk和Wv的大小为（d_model，d_model）。按照上面的示例，它们的形状为（512，512）。

因此，可以更好地理解乘法的输出。每个重量矩阵同时在批处理中 broadcast 每个序列，以创建Q，K和V张量。

• Q = XWq | (batch_size, seq_length, d_model) x (d_model, d_model) = (batch_size, seq_length, d_model)
• K = XWk | (batch_size, seq_length, d_model) x (d_model, d_model) = (batch_size, seq_length, d_model)
• V = XWv | (batch_size, seq_length, d_model) x (d_model, d_model) = (batch_size, seq_length, d_model)

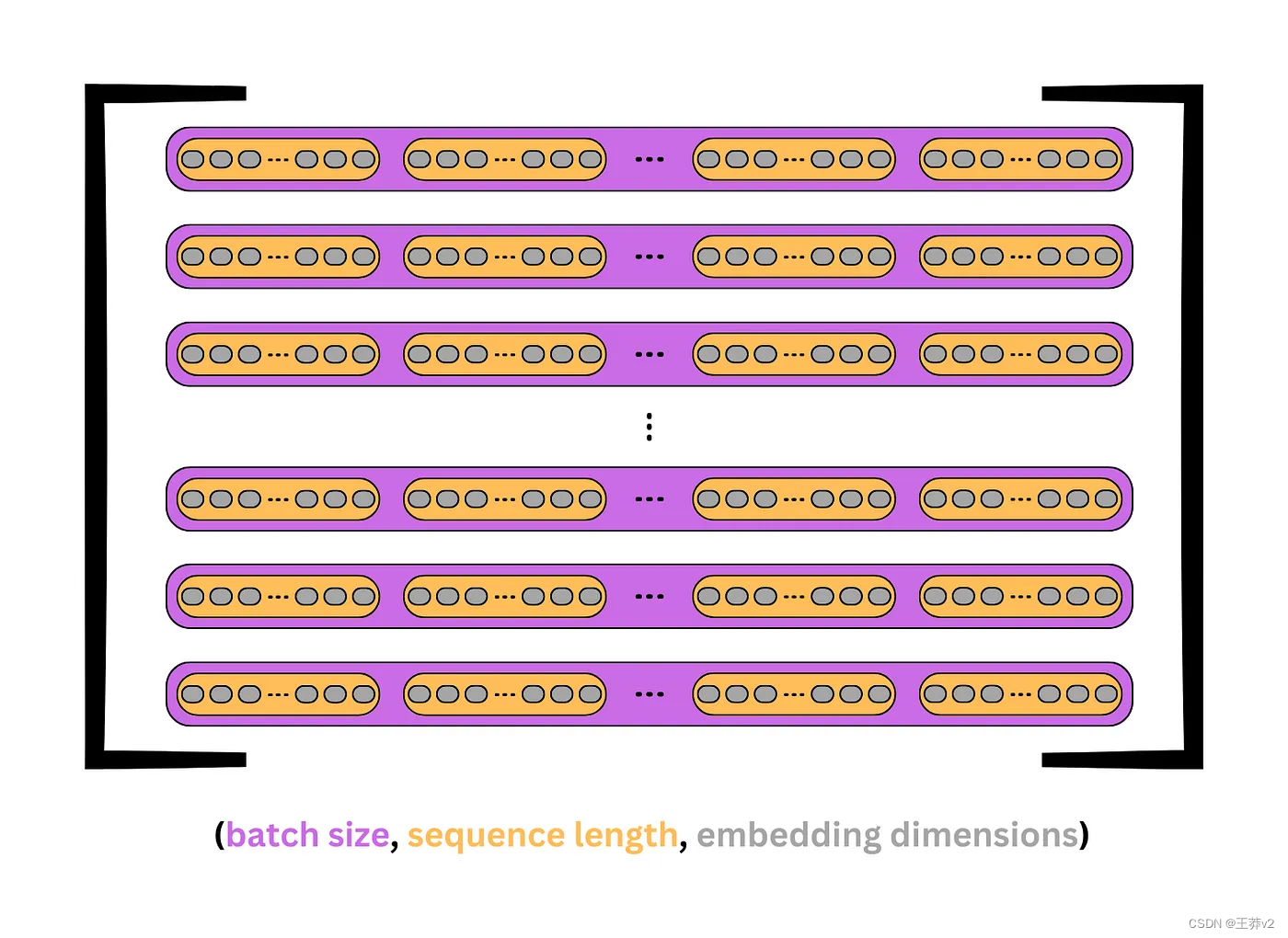
下面的图片显示了Q, K和V是如何出现的。每个紫色盒子代表一个序列，每个橙色盒子是序列中的一个 token 或单词。灰色椭圆表示每个token 的嵌入。

下面的代码加载了Positional Encoding和Embeddings类。

# convert the sequences to integers
sequences = ["I wonder what will come next!",
             "This is a basic example paragraph.",
             "Hello, what is a basic split?"]

# tokenize the sequences
tokenized_sequences = [tokenize(seq) for seq in sequences]

# index the sequences 
indexed_sequences = [[stoi[word] for word in seq] for seq in tokenized_sequences]

# convert the sequences to a tensor
tensor_sequences = torch.tensor(indexed_sequences).long()

# vocab size
vocab_size = len(stoi)

# embedding dimensions
d_model = 8

# create the embeddings
lut = Embeddings(vocab_size, d_model) # look-up table (lut)

# create the positional encodings
pe = PositionalEncoding(d_model=d_model, dropout=0.1, max_length=10)

# embed the sequence
embeddings = lut(tensor_sequences)

# positionally encode the sequences
X = pe(embeddings)

tensor([[[-3.45, -1.34,  4.12, -3.33, -0.81, -1.93, -0.28,  8.25],
         [ 7.36, -1.09,  2.32,  1.52,  3.50,  1.42,  0.46, -0.95],
         [-2.26,  0.53, -1.02,  1.49, -3.97, -2.19,  2.86, -0.59],
         [-3.87, -2.02,  1.46,  6.78,  0.88,  1.08, -2.97,  1.45],
         [ 1.12, -2.09,  1.19,  3.87, -0.00,  3.73, -0.88,  1.12],
         [-0.35, -0.02,  3.98, -0.20,  7.05,  1.55,  0.00, -0.83]],

        [[-4.27,  0.17, -2.08,  0.94, -6.35,  1.99,  5.23,  5.18],
         [-0.00, -5.05, -7.19,  3.27,  1.49, -7.11, -0.59,  0.52],
         [ 0.54, -2.33, -1.10, -2.02, -0.88, -3.15,  0.38,  5.26],
         [ 0.87, -2.98,  2.67,  3.32,  1.16,  0.00,  1.74,  5.28],
         [-5.58, -2.09,  0.96, -2.05, -4.23,  2.11, -0.00,  0.61],
         [ 6.39,  2.15, -2.78,  2.45,  0.30,  1.58,  2.12,  3.20]],

        [[ 4.51, -1.22,  2.04,  3.48,  1.63,  3.42,  1.21,  2.33],
         [-2.34,  0.00, -1.13,  1.51, -3.99, -2.19,  2.86, -0.59],
         [-4.65, -6.12, -7.08,  3.26,  1.50, -7.11, -0.59,  0.52],
         [-0.32, -2.97, -0.99, -2.05, -0.87, -0.00,  0.39,  5.26],
         [-0.12, -2.61,  2.77,  3.28,  1.17,  0.00,  1.74,  5.28],
         [-5.64,  0.49,  2.32, -0.00, -0.44,  4.06,  3.33,  3.11]]],
       grad_fn=<MulBackward0>)

此时，嵌入序列X的形状为(3,6,8)。有3个序列，包含6个标记，具有8维嵌入。

Wq、Wk和Wv的线性层可以使用nn.Linear(d_model, d_model)来创建。这将创建一个(8,8)矩阵，该矩阵将在跨每个序列的乘法期间广播。

Wq = nn.Linear(d_model, d_model)          # query weights (8,8)
Wk = nn.Linear(d_model, d_model)          # key weights   (8,8)
Wv = nn.Linear(d_model, d_model)          # value weights (8,8)

Wq.state_dict()['weight']

tensor([[ 0.19,  0.34, -0.12, -0.22,  0.26, -0.06,  0.12, -0.28],
        [ 0.09,  0.22,  0.32,  0.11,  0.21,  0.03, -0.35,  0.31],
        [-0.34, -0.21, -0.11,  0.34, -0.28,  0.03,  0.26, -0.22],
        [-0.35,  0.11,  0.17,  0.21, -0.19, -0.29,  0.22,  0.20],
        [ 0.19,  0.04, -0.07, -0.02,  0.01, -0.20,  0.30, -0.19],
        [ 0.23,  0.15,  0.22,  0.26,  0.17,  0.16,  0.23,  0.18],
        [ 0.01,  0.06, -0.31,  0.19,  0.22,  0.08,  0.15, -0.04],
        [-0.11,  0.24, -0.20,  0.26, -0.01, -0.14,  0.29, -0.32]])

Wq的权重如上图所示。Wk和Wv形状相同，但权重不同。当X穿过每一个线性层时，它保持它的形状，但是现在Q, K和V已经被权值转换成唯一的张量。

Q = Wq(X) # (3,6,8)x(broadcast 8,8) = (3,6,8)
K = Wk(X) # (3,6,8)x(broadcast 8,8) = (3,6,8)
V = Wv(X) # (3,6,8)x(broadcast 8,8) = (3,6,8)

Q

tensor([
        # sequence 0
        [[-3.13,  2.71, -2.07,  3.54, -2.25, -0.26, -2.80, -4.31],
         [ 1.70,  1.63, -2.90, -2.90,  1.15,  3.01,  0.49, -1.14],
         [-0.69, -2.38,  3.00,  3.09,  0.97, -0.98, -0.10,  2.16],
         [-3.52,  2.08,  2.36,  2.16, -2.48,  0.58,  0.33, -0.26],
         [-1.99,  1.18,  0.64, -0.45, -1.32,  1.61,  0.28, -1.18],
         [ 1.66,  2.46, -2.39, -0.97, -0.47,  1.83,  0.36, -1.06]],
        # sequence 1
        [[-3.13, -2.43,  3.85,  4.34, -0.60, -0.03,  0.04,  0.62],
         [-0.82, -2.67,  1.82,  0.89,  1.30, -2.65,  2.01,  1.56],
         [-1.42,  0.11, -1.40,  1.36, -0.21, -0.87, -0.88, -2.24],
         [-2.70,  1.88, -0.10,  1.95, -0.75,  2.54, -0.14, -1.91],
         [-2.67, -1.58,  2.46,  1.93, -1.78, -2.44, -1.76, -1.23],
         [ 1.23,  0.78, -1.93, -1.12,  1.07,  2.98,  1.82,  0.18]],
        # sequence 2
        [[-0.71,  1.90, -1.12, -0.97, -0.23,  3.54,  0.65, -1.39],
         [-0.87, -2.54,  3.16,  3.04,  0.94, -1.10, -0.10,  2.07],
         [-2.06, -3.30,  3.63,  2.39,  0.38, -3.87,  1.86,  1.79],
         [-2.00,  0.02, -0.90,  0.68, -1.03, -0.63, -0.70, -2.77],
         [-2.76,  1.90,  0.14,  2.34, -0.93,  2.38, -0.17, -1.75],
         [-1.82,  0.15,  1.79,  2.87, -1.65,  0.97, -0.21, -0.54]]],
       grad_fn=<ViewBackward0>)

Q K和V都是这个形状。和前面一样，每个矩阵是一个序列，每一行都是由嵌入表示的 token。

把Q, K, V分成多头

通过创建Q，K和V张量，现在可以通过将D_Model的视图更改为 (n_heads, d_key) 将它们分为各自的头部。N_heads可以是任意数字，但是使用较大的嵌入时，通常要执行8、10或12。请记住，d_key = (d_model / n_heads)。

在前面的图像中，每个 token 在单个维度中包含d_model嵌入。现在，这个维度被分成行和列来创建一个矩阵；每行是一个包含键的头。这可以从上面的图片中看到。

每个张量的形状变成：

• (batch_size, seq_length, d_model) → (batch_size, seq_length, n_heads, d_key)

假设示例中选择了四个heads，则(3,6,8)张量将被分成(3,6,4,2)张量，其中有3个序列，每个序列中有6个tokens，每个标记中有4个heads，每个正面中有2个元素。

这可以通过view来实现，它可以用来添加和设置每个维度的大小。由于每个示例的批大小或序列数量是相同的，因此可以设置批大小。同样，在每个张量中，头的数量和键的数量应该是恒定的。-1可用于表示剩余值，即序列长度。

batch_size = Q.size(0)   
n_heads = 4
d_key = d_model//n_heads # 8/4 = 2

# query tensor | -1 = query_length | (3, 6, 8) -> (3, 6, 4, 2)
Q = Q.view(batch_size, -1, n_heads, d_key)

# value tensor | -1 = key_length | (3, 6, 8) -> (3, 6, 4, 2) 
K = K.view(batch_size, -1, n_heads