1.9 数据结构之 并查集

编程总结

在刷题之前需要反复练习的编程技巧，尤其是手写各类数据结构实现，它们好比就是全真教的上乘武功
本栏目为学习笔记参考：https://leetcode.cn/leetbook/read/disjoint-set/oviefi/

1.0 概述

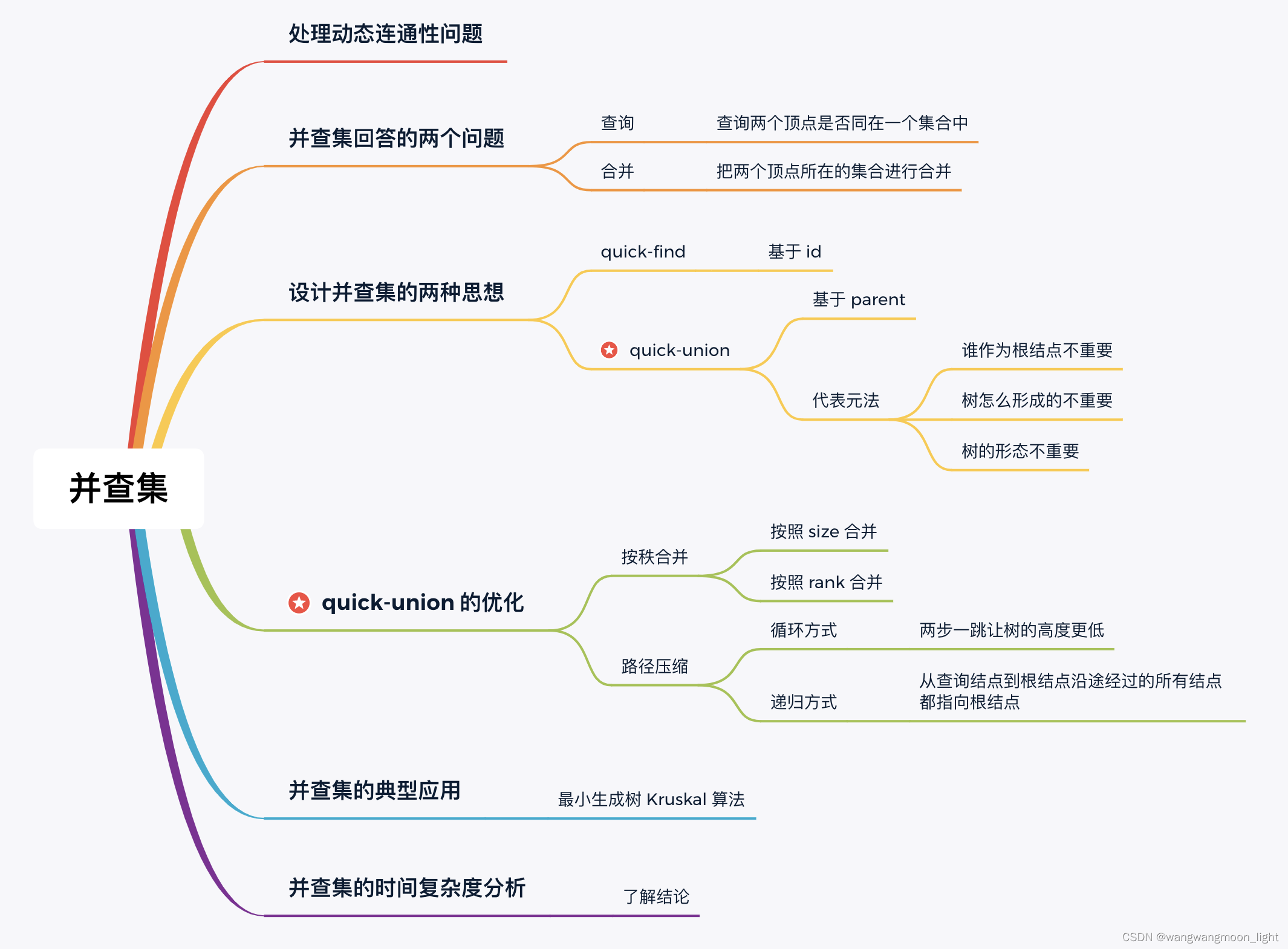
并查集（Union Find）也叫「不相交集合（Disjoint Set）」，专门用于 动态处理 不相交集合的「查询」与「合并」问题。

很多数据结构都因为具有 动态 处理问题的能力而变得高效，例如「堆」「二叉查找树」等。所谓「动态」的意思是：要处理的数据不是一开始就确定好的，理解「并查集」动态处理数据的最好的例子是「最小生成树」算法（本专题第 3 节介绍）。

可以使用并查集的问题一般都可以使用基于遍历的搜索算法（深度优先搜索、广度优先搜索）完成，但是使用并查集会使得解决问题的过程更加清晰、直观。

并查集的问题属于竞赛级别需要掌握的数据结构，但其本身代码量少且好理解，但难在应用。目前看来「并查集」不是普通公司面试和笔试的考点，请大家合理分配时间进行学习。

基本概念

我们以一个直观的问题引入并查集 (不相交集) 的概念。

※ 并查集: Union-Find Set ，不相交集: Disjoint Set。

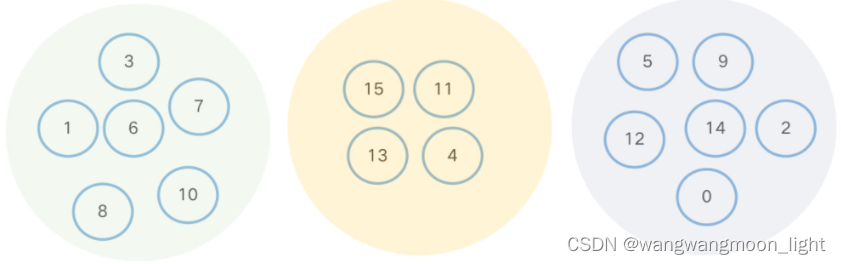
亲戚问题： 有一群人，他们属于不同家族，同一个家族里的人互为亲戚，不同家族的人不是亲戚。已知每个人都知道自己与其他人是否有亲戚关系，求问有几个家族。

亲戚问题代表着一大类能用并查集解决的所谓确定「连通分量」的问题，可以将上述问题图示化如下，不同颜色的集合代表不同家族，集合内的人 (元素) 互为亲戚。从图论的角度来说，同一个集合内的元素是相互「连通」的，那么一个集合就是一个「连通分量」。用集合的语言来说，问题涉及的元素可划归到互相 没有交集 的集合，因此也称这样的结构为 「不相交集」

于是我们可以这样概括性地描述并查集：

并查集 (不相交集) 是一种描述不相交集合的数据结构，即若一个问题涉及多个元素，它们可划归到不同集合，同属一个集合内的元素等价（即可用任意一个元素作为代表，比如上述的互为亲戚即互相等价），不同集合内的元素不等价。

这基本上就是对并查集的完整描述了，十分简单。问题涉及的元素初始时总是自己构成一个单元素集合，求解问题需要通过合并操作将等价元素归入一个集合中。为了能够合并等价元素，我们必须查询希望合并的对象元素属于哪个集合，以决定是否要执行合并。因此 主要操作就是「查询」与「合并」 (注意，此刻我们当然还不知道如何查询如何求并，但并不妨碍我们看出这两个操作的必要性) 。

「不相交」描述的是问题元素构成集合之后各个集合不相交的状态，「并查」描述的是处理问题时的操作。后文中两种称呼都会出现。

上面的亲戚问题只用于引入并查集的概念，而本文剩下的内容，会以 547: 省份数量 问题为研究对象，一步步 发明并查集 以解决该问题。

在「并查集」数据结构中，其中心思想是将所有连接的顶点，无论是直接连接还是间接连接，都将他们指向同一个父节点或者根节点。此时，如果要判断两个顶点是否具有连通性，只要判断它们的根节点是否为同一个节点即可。

在「并查集」数据结构中，它的两个灵魂函数，分别是 find和 union。find 函数是为了找出给定顶点的根节点。 union 函数是通过更改顶点根节点的方式，将两个原本不相连接的顶点表示为两个连接的顶点。对于「并查集」来说，它还有一个重要的功能性函数 connected。它最主要的作用就是检查两个顶点的「连通性」。find 和 union 函数是「并查集」中必不可少的函数。connected 函数则需要根据题目的意思来决定是否需要

public class UnionFind {
    // UnionFind 的构造函数，size 为 root 数组的长度
    public UnionFind(int size) {}
    public int find(int x) {}
    public void union(int x, int y) {}
    public boolean connected(int x, int y) {}
}

「并查集」的 find 函数

// 1.find 函数的基本实现
public int find(int x) {
    while (x != root[x]) {
        x = root[x];
    }
    return x;
}
// 2.find 函数的优化 - 路径压缩
public int find(int x) {
    if (x == root[x]) {
        return x;
    }
    return root[x] = find(root[x]);
}

「并查集」的 union 函数

它主要是连接两个顶点 x 和 y 。将它们的根结点变成相同的，即代表它们来自于同一个根节点。
union 函数的基本实现

// 1. union函数的基本实现
public void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        root[rootY] = x;
    }
};
// 2.union函数的优化 -- 按秩合并
public void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        if (rank[rootX] > rank[rootY]) {
            root[rootY] = rootX;
        } else if (rank[rootX] < rank[rootY]) {
            root[rootX] = rootY;
        } else {
            root[rootY] = rootX;
            rank[rootX] += 1;
        }
    }
};

「并查集」的 connected 函数

它主要是检查两个顶点 x 和 y 的「连通性」。这个函数通过顶点 x 和 y 的根结点是否相同来判断 x 和 y 的「连通性」。如果 x 和 y 的根结点相同，则为连通。反之，则为不连通。

public boolean connected(int x, int y) {
    return find(x) == find(y);
}

「并查集」的代码是高度模版化的。所以作者建议大家熟记「并查集」的实现代码，这样小伙伴们在遇到「并查集」的算法题目的时候，就可以淡定的应对了。作者推荐大家在理解的前题下，请熟记「基于路径压缩+按秩合并的并查集」的实现代码。

最后，请小伙伴们尝试用「并查集」以及刚刚熟记的代码，实现后面「并查集」相关的练习题。虽然，一道算法题可以有很多种解法，但是作者还是非常建议大家用「并查集」的思想实现该章节的算法练习题哦。

547. 省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。
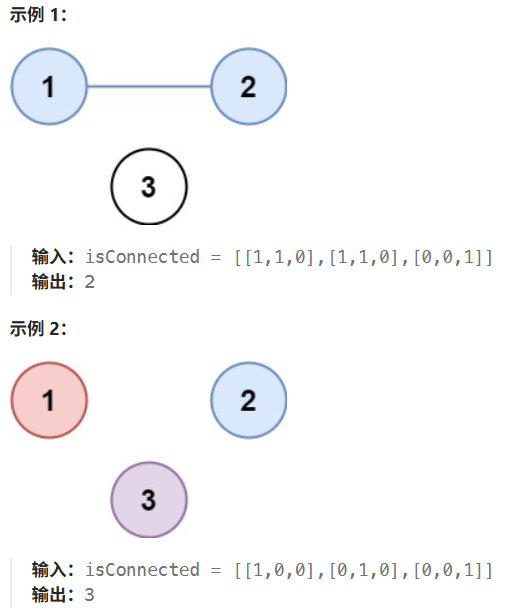
给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。

int Find(int *root, int x)
{
    if (x == root[x]) {
        return x;
    }
    root[x] = Find(root, root[x]);
    return root[x];
}
void Union(int *root, int x, int y)
{
    // 基于路径压缩优化的并查集
    int rootX = Find(root, x);
    int rootY = Find(root, y);
    if (rootX != rootY) {
        root[rootY] = rootX;
    }
}
void UnionFind(int *root, int size)
{
    // 初始化：每个元素的父节点都是本身
    for (int i = 0; i < size; i++) {
        root[i] = i;
    }
}
int findCircleNum(int **isConnected, int isConnectedSize, int *isConnectedColSize)
{
    int cities = isConnectedSize;
    int root[cities];
    UnionFind(root, cities);
    for (int i = 0; i < cities; i++) {
        for (int j = i + 1; j < cities; j++) {
            if (isConnected[i][j] == 1) {
                Union(root, i, j);
            }
        }
    }
    int provinces = 0;
    for (int i = 0; i < cities; i++) {
        if (root[i] == i) {
            provinces++;
        }
    }
    return provinces;
}
int main(void)
{
    int tmp0[3][3] = {{1,1,1}, {1,1,1}, {1,1,1}};
    int **isConnected = (int **)malloc(sizeof(int *)* 3);
    for (int i = 0; i < 3; i++) {
        isConnected[i] = (int *)malloc(sizeof(int) * 3);
        isConnected[i] = tmp0[i];
    }
    int isConnectedSize = 3;
    int isConnectedColSize = 3;
    int ret = findCircleNum(isConnected, isConnectedSize, &isConnectedColSize);
    (void)printf("%d\n", ret);
    return 0;
}