编程总结
在刷题之前需要反复练习的编程技巧,尤其是手写各类数据结构实现,它们好比就是全真教的上乘武功。
本学习来自 leetcode,整理提炼.
https://leetcode-cn.com/leetbook/read/queue-stack/kyozi/
广度优先搜索(BFS)是一种遍历或搜索数据结构(如树或图)的算法。
如前所述,我们可以使用 BFS 在树中执行层序遍历。
我们也可以使用 BFS 遍历图。例如,我们可以使用 BFS 找到从起始结点到目标结点的路径,特别是最短路径。
我们可以在更抽象的情景中使用 BFS 遍历所有可能的状态。在这种情况下,我们可以把状态看作是图中的结点,而以合法的过渡路径作为图中的边。
解释队列和BFS的关系.
广度优先搜索(BFS)的一个常见应用是找出从根结点到目标结点的最短路径。
- 结点的处理顺序是什么?
在第一轮中,我们处理根结点。在第二轮中,我们处理根结点旁边的结点;在第三轮中,我们处理距根结点两步的结点;等等等等。
与树的层序遍历类似,越是接近根结点的结点将越早地遍历。
如果在第 k 轮中将结点 X 添加到队列中,则根结点与 X 之间的最短路径的长度恰好是 k。也就是说,第一次找到目标结点时,你已经处于最短路径中。
- 队列的入队和出队顺序是什么?
如上面的动画所示,我们首先将根结点排入队列。然后在每一轮中,我们逐个处理已经在队列中的结点,并将所有邻居添加到队列中。值得注意的是,新添加的节点不会立即遍历,而是在下一轮中处理。
结点的处理顺序与它们添加到队列的顺序是完全相同的顺序,即先进先出(FIFO)。这就是我们在 BFS 中使用队列的原因。
广度优先搜索 - 模板
之前,我们已经介绍了使用 BFS 的两个主要方案:遍历或找出最短路径。通常,这发生在树或图中。正如我们在章节描述中提到的,BFS 也可以用于更抽象的场景中。在本文中,我们将为你提供一个模板。然后,我们在本文后提供一些习题供你练习。在特定问题中执行 BFS 之前确定结点和边缘非常重要。通常,结点将是实际结点或是状态,而边缘将是实际边缘或可能的转换。
286. 墙与门_多源BFS_90%
你被给定一个 m × n 的二维网格 rooms ,网格中有以下三种可能的初始化值:
-1 表示墙或是障碍物
0 表示一扇门
INF 无限表示一个空的房间。
然后,我们用 2^31 - 1 = 2147483647 代表 INF。
你可以认为通往门的距离总是小于 2147483647 的。
你要给每个空房间位上填上该房间到 最近门的距离 ,如果无法到达门,则填 INF 即可


手法1:为什么多源BFS下,访问到的距离一定是最近门的距离呢
对于网格中的每个房间,如果在第 k 轮被首次访问到,则当前房间到最近门的距离是 k。理由如下:如果当前房间到最近门的距离小于 k,则从最近的门开始访问到当前房间的轮数一定小于 k,因此当前房间被首次访问到的轮数小于 k,与当前房间在第 k 轮被首次访问到矛盾。因此网格中的每个房间被首次访问到的轮数即为到最近门的距离。
遍历结束之后,即可得到每个房间到最近门的距离。
// 反向思维,从门开始找
typedef struct {
int x;
int y;
int step;
} Node;
void wallsAndGates(int **rooms, int roomsSize, int *roomsColSize)
{
if ((roomsSize == 0) || (*roomsColSize == 0)) {
return;
}
int row = roomsSize;
int col = *roomsColSize;
int direction[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; // 下上右左,四个方向
Node *queue = (Node *)malloc(sizeof(Node) * row * col);
int head = 0;
int tail = 0;
int i, j;
// 1. 门节点都入队列.
for (i = 0; i < row; i++) {
for (j = 0; j < col; j++) {
if (rooms[i][j] == 0) {
queue[tail].x = i;
queue[tail].y = j;
queue[tail++].step = 0;
}
}
}
// 2. 以门为起点开始BFS,利用该门节点遍历所有“岛”节点(这里借助了第200题岛的概念)
// 循环迭代直到队列为空
while (tail != head) {
int xx = queue[head].x;
int yy = queue[head].y;
int curStep = queue[head++].step; // 门节点出队列
for (i = 0; i < 4; i++) {
int xNext = xx + direction[i][0];
int yNext = yy + direction[i][1];
if ((xNext >= 0) && (xNext < row) && (yNext >= 0) && (yNext < col) && (rooms[xNext][yNext] == INT_MAX)) {
rooms[xNext][yNext] = curStep + 1;
queue[tail].x = xNext;
queue[tail].y = yNext;
queue[tail++].step = curStep + 1; // 将当前出队的元素相邻元素入队
}
}
}
}
int main()
{
int **rooms = (int **)malloc(sizeof(int **));
int roomsSize = 4;
int roomsColSize = 4;
for (int i = 0; i < 4; i++) {
rooms[i] = (int *)malloc(sizeof(int) * 4);
}
int rooms0[4] = { 2147483647, -1, 0, 2147483647 };
int rooms1[4] = { 2147483647, 2147483647, 2147483647, -1 };
int rooms2[4] = { 2147483647, -1, 2147483647, -1 };
int rooms3[4] = { 0, -1, 2147483647, 2147483647 };
rooms[0] = rooms0;
rooms[1] = rooms1;
rooms[2] = rooms2;
rooms[3] = rooms3;
wallsAndGates(rooms, roomsSize, &roomsColSize);
for (int i = 0; i < roomsSize; i++) {
for (int j = 0; j < roomsColSize; j++) {
printf("%02d ", rooms[i][j]);
}
printf("\n");
}
return 0;
}
200. 岛屿数量_90%
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。

手法1:BFS:凡是能遍历到的节点,均是一个岛屿上的
BFS : 思路是线性扫描整个二维网络,如果一个节点包含1,则以其为根节点启动BFS. 并将其设为2(FLAG_NUM)以标记访问过该节点,迭代地搜索队列中的每一个节点,直到队列为空 – 凡是能遍历到的都是一个岛上的. 继续此方法遍历二维网络其他点找其他岛,遍历完后就能找到所有“岛”的数量
#define NUM_2 2
typedef struct node {
int x;
int y;
} Node;
Node queue[300 * 300] = { 0 };
int head = 0;
int tail = 0;
void BFS(char **grid, int gridSize, int *gridColSize)
{
int direction[4][2] = { {1,0}, {0,1}, {-1,0}, {0,-1} };
while (tail != head) { // 不是 head <= tail
int xx = queue[head].x;
int yy = queue[head].y;
head++;
for (int i = 0; i < 4; i++) {
int xNext = xx + direction[i][0];
int yNext = yy + direction[i][1];
if ((xNext >= 0) && (xNext < gridSize) && (yNext >= 0) && (yNext < *gridColSize) && (grid[xNext][yNext] == '1')) {
queue[tail].x = xNext;
queue[tail].y = yNext;
grid[xNext][yNext] = '0' + NUM_2;
tail++;
}
}
}
}
int numIslands(char **grid, int gridSize, int *gridColSize)
{
int result = 0;
for (int i = 0; i < gridSize; i++) {
for (int j = 0; j < *gridColSize; j++) {
if (grid[i][j] == '1') {
queue[tail].x = i;
queue[tail].y = j;
tail++;
BFS(grid, gridSize, gridColSize);
result++;
}
}
}
return result;
}
int main(void)
{
char **grid = NULL;
int gridSize = 4;
int gridColSize = 5;
grid = (char **)malloc(sizeof(char *));
for (int i = 0; i < 4; i++) {
grid[i] = (char *)malloc(sizeof(char) * 5);
}
grid[0][0] = '1';
grid[0][1] = '1';
grid[0][2] = '1';
grid[0][3] = '1';
grid[0][4] = '0';
grid[1][0] = '1';
grid[1][1] = '1';
grid[1][2] = '0';
grid[1][3] = '1';
grid[1][4] = '0';
grid[2][0] = '1';
grid[2][1] = '1';
grid[2][2] = '0';
grid[2][3] = '0';
grid[2][4] = '0';
grid[3][0] = '0';
grid[3][1] = '0';
grid[3][2] = '0';
grid[3][3] = '0';
grid[3][4] = '0';
printf("result %d\n", numIslands(grid, gridSize, &gridColSize));
return 0;
}
手法2:DFS
#define MAXSIZE 300
int g_direction[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
void DFS(char **grid, int gridSize, int colSize, int **visited, int x, int y)
{
if (x < 0 || x >= gridSize || y < 0 || y >= colSize) {
return;
}
if (grid[x][y] == '1' && !visited[x][y]) {
visited[x][y] = 1;
for (int i = 0; i < 4; i++) {
DFS(grid, gridSize, colSize, visited, x + g_direction[i][0], y + g_direction[i][1]);
}
}
}
int numIslands(char **grid, int gridSize, int *gridColSize) {
int count = 0;
int colSize = *gridColSize;
int **visited = (int **)malloc(sizeof(int *)*MAXSIZE);
for (int i = 0; i < MAXSIZE; i++) {
visited[i] = (int *)malloc(sizeof(int)*MAXSIZE);
memset(visited[i], 0, sizeof(int) * MAXSIZE);
};
for (int i = 0; i < gridSize; i++) {
for (int j = 0; j < colSize; j++) {
if (grid[i][j] == '1' && !visited[i][j]) {
DFS(grid, gridSize, colSize, visited, i, j);
count++;
}
}
}
return count;
}
752. 打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。
每个拨轮都有10个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。
每个拨轮可以自由旋转:例如把 ‘9’ 变为 ‘0’,‘0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000’ ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#define KEY_LENTH 4
#define QUEUE_LENTH 10000
typedef struct {
char key[KEY_LENTH + 1];
} Node;
// 构造循环队列
typedef struct {
Node *base;
int head;
int tail;
int MaxSize;
} Queue;
Queue *QueueCreate(int k)
{
Queue *obj = (Queue *)malloc(sizeof(Queue));
if (obj == NULL) {
return NULL;
}
obj->base = (Node *)malloc(sizeof(Node) * (k + 1));
memset(obj->base, 0, sizeof(Node) * (k + 1));
obj->head = 0;
obj->tail = 0;
obj->MaxSize = k + 1;
return obj;
}
bool QueueIsEmpty(Queue *obj)
{
if (obj->head == obj->tail) {
return true;
}
return false;
}
bool QueueIsFull(Queue *obj)
{
return ((obj->tail + 1) == obj->head);
}
bool QueueEnQueue(Queue *obj, Node value)
{
if (QueueIsFull(obj) == true) {
return false;
}
obj->base[obj->tail] = value;
obj->tail = (obj->tail + 1) % obj->MaxSize;
return true;
}
bool QueueDeQueue(Queue *obj)
{
if (QueueIsEmpty(obj) == true) {
return false;
}
obj->head = (obj->head + 1) % obj->MaxSize;
return true;
}
Node QueueFront(Queue *obj)
{
return obj->base[obj->head];
}
Node QueueTail(Queue *obj)
{
return obj->base[(obj->tail - 1)];
}
int QueueSize(Queue *obj)
{
if (obj->head > obj->tail) {
return obj->tail + obj->MaxSize - obj->head;
}
return obj->tail - obj->head;
}
void QueueFree(Queue *obj)
{
if (obj->base) {
free(obj->base);
}
obj->base = NULL; // 先释放指针,并赋值NULL
obj->head = 0;
obj->tail = 0;
free(obj);
}
// ----------------------------- //
Queue *gQueue;
int gVisited[QUEUE_LENTH];
int Str2Int(char *s, int len)
{
int ret = 0;
for (int i = 0; i < len; i++) {
ret = ret * 10;
ret = ret + s[i] - '0';
}
return ret;
}
bool IsTarget(char *str, char *target)
{
return !strcmp(str, target);
}
void InitVisitDead(char **deadends, int deadendsSize)
{
for (int i = 0; i < deadendsSize; i++) {
int index = atoi(deadends[i]);
gVisited[index] = 1;
}
}
bool isInDead(char *str, char **deadends, int deadendsSize)
{
for (int i = 0; i < deadendsSize; i++) {
if (IsTarget(str, deadends[i]) == true) {
return true;
}
}
return false;
}
void GetNextNodeEnQueue(Queue *obj, char *str, char **deadends, int deadendsSize)
{
/* 基于当前数字产生新的8位数字(各个位置前后旋转) */
for (int i = 0; i < KEY_LENTH; i++) {
for (int step = -1; step <= 1; step += 2) {
char nextCode[KEY_LENTH + 1];
memcpy(nextCode, str, 5);
nextCode[KEY_LENTH] = '\0';
nextCode[i] = (nextCode[i] - '0' + step + 10) % 10 + '0';
int index = atoi(nextCode);
if (isInDead(nextCode, deadends, deadendsSize) == true || gVisited[index] == 1) {
continue;
}
Node enNode;
memcpy(enNode.key, nextCode, 5);
QueueEnQueue(gQueue, enNode);
gVisited[index] = 1;
}
}
}
int openLock(char **deadends, int deadendsSize, char *target)
{
int steps = 0;
char *str = (char *)"0000";
if (isInDead(str, deadends, deadendsSize) == true) {
return -1;
}
gQueue = QueueCreate(QUEUE_LENTH);
memset(gVisited, 0, QUEUE_LENTH * sizeof(int));
InitVisitDead(deadends, deadendsSize);
// 将起点"0000"入队列
Node enNode;
memcpy(enNode.key, str, 5);
QueueEnQueue(gQueue, enNode);
gVisited[0] = 1;
if (strcmp(str, target) == 0) {
return 0;
}
// 遍历队列
while (QueueIsEmpty(gQueue) == false) {
steps++;
int queueSize = QueueSize(gQueue);
for (int i = 0; i < queueSize; i++) { // 遍历已在队列中的节点
Node deNode;
deNode = QueueFront(gQueue);
QueueDeQueue(gQueue);
// 获取当前值的邻接值,判断是否在黑名单中,如不在,入队列
// 基于当前数字产生新的8位数字(各个位置前后旋转)
for (int i = 0; i < KEY_LENTH; i++) {
for (int step = -1; step <= 1; step += 2) {
char nextCode[KEY_LENTH + 1];
memcpy(nextCode, deNode.key, 5);
nextCode[KEY_LENTH] = '\0';
nextCode[i] = (nextCode[i] - '0' + step + 10) % 10 + '0'; // 这个手法的处理也是可以
int index = atoi(nextCode);
if (IsTarget(nextCode, target) == true) {
return steps;
}
if (gVisited[index] == 1) {
continue;
}
Node enNode; // 建立新的结点并入队列
memcpy(enNode.key, nextCode, 5);
QueueEnQueue(gQueue, enNode);
gVisited[index] = 1;
}
}
}
}
QueueFree(gQueue);
return -1;
}
int main(void)
{
char **deadends =(char **)malloc(sizeof(char *) * 5);
char *target = (char *)"0000";
int deadendsSize = 4;
for (int i = 0; i < 5; i++) {
deadends[i] = (char *)malloc(sizeof(char)*5);
}
memcpy(deadends[0], "0201", 5);
memcpy(deadends[1], "0101", 5);
memcpy(deadends[2], "0102", 5);
memcpy(deadends[3], "1212", 5);
memcpy(deadends[4], "2002", 5);
openLock(deadends, deadendsSize, target);
return 0;
}
130. 被围绕的区域_90%
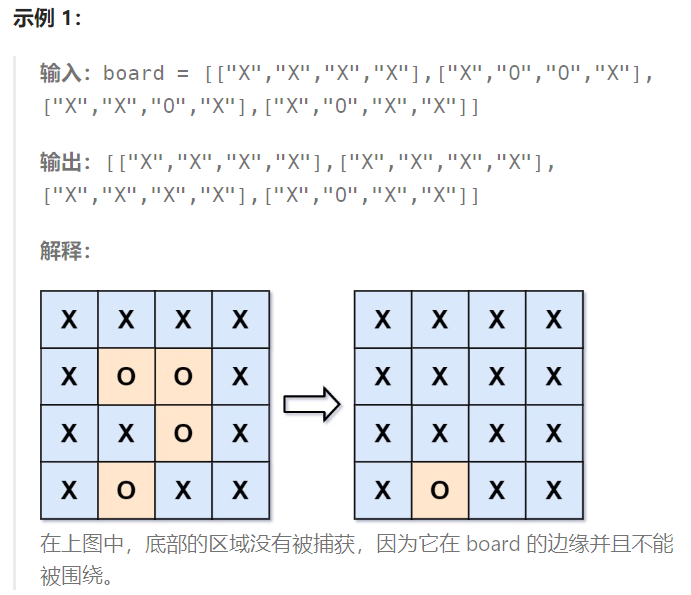
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ 组成,捕获 所有 被围绕的区域:
连接:一个单元格与水平或垂直方向上相邻的单元格连接。
区域:连接所有 ‘O’ 的单元格来形成一个区域。
围绕:如果您可以用 ‘X’ 单元格 连接这个区域,并且区域中没有任何单元格位于 board 边缘,则该区域被 ‘X’ 单元格围绕。
通过 原地 将输入矩阵中的所有 ‘O’ 替换为 ‘X’ 来 捕获被围绕的区域。你不需要返回任何值。
#define NUM_2 2
typedef struct node {
int x;
int y;
} Node;
Node queue[200 * 200] = { 0 };
int head = 0;
int tail = 0;
void BFS(char **board, int gridSize, int *gridColSize)
{
int direction[4][2] = { {1,0}, {0,1}, {-1,0}, {0,-1} };
while (tail != head) { // 不是 head <= tail
int xx = queue[head].x;
int yy = queue[head].y;
head++;
for (int i = 0; i < 4; i++) {
int xNext = xx + direction[i][0];
int yNext = yy + direction[i][1];
if ((xNext >= 0) && (xNext < gridSize) && (yNext >= 0) && (yNext < *gridColSize) && (board[xNext][yNext] == 'O')) {
queue[tail].x = xNext;
queue[tail].y = yNext;
board[xNext][yNext] = 'A';
tail++;
}
}
}
}
void solve(char **board, int boardSize, int *boardColSize)
{
for (int i = 0; i < boardSize; i++) {
for (int j = 0; j < *boardColSize; j++) {
// 从边缘入手
if ((board[i][j] == 'O') && ((i == 0) || (j == 0) || (i == (boardSize - 1)) || (j == (*boardColSize - 1)))) {
queue[tail].x = i;
queue[tail].y = j;
board[i][j] = 'A';
tail++;
BFS(board, boardSize, boardColSize);
}
}
}
for (int i = 0; i < boardSize; i++) {
for (int j = 0; j < *boardColSize; j++) {
if (board[i][j] == 'A') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
int main(void)
{
char **grid = NULL;
int gridSize = 4;
int gridColSize = 4;
grid = (char **)malloc(sizeof(char *));
for (int i = 0; i < 4; i++) {
grid[i] = (char *)malloc(sizeof(char) * 4);
}
grid[0][0] = 'X';
grid[0][1] = 'X';
grid[0][2] = 'X';
grid[0][3] = 'X';
grid[1][0] = 'X';
grid[1][1] = 'O';
grid[1][2] = 'O';
grid[1][3] = 'X';
grid[2][0] = 'X';
grid[2][1] = 'X';
grid[2][2] = 'O';
grid[2][3] = 'X';
grid[3][0] = 'X';
grid[3][1] = 'O';
grid[3][2] = 'X';
grid[3][3] = 'X';
solve(grid, gridSize, &gridColSize);
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
printf("%C ", grid[i][j]);
}
printf("\n");
}
return 0;
}
490. 迷宫
由空地(用 0 表示)和墙(用 1 表示)组成的迷宫 maze 中有一个球。球可以途经空地向 上、下、左、右 四个方向滚动,且在遇到墙壁前不会停止滚动。当球停下时,可以选择向下一个方向滚动。
给你一个大小为 m x n 的迷宫 maze ,以及球的初始位置 start 和目的地 destination ,其中 start = [start-row, start-col] 且 destination = [destination-row, destination-col] 。请你判断球能否在目的地停下:如果可以,返回 true ;否则,返回 false 。
你可以 假定迷宫的边缘都是墙壁(参考示例)。
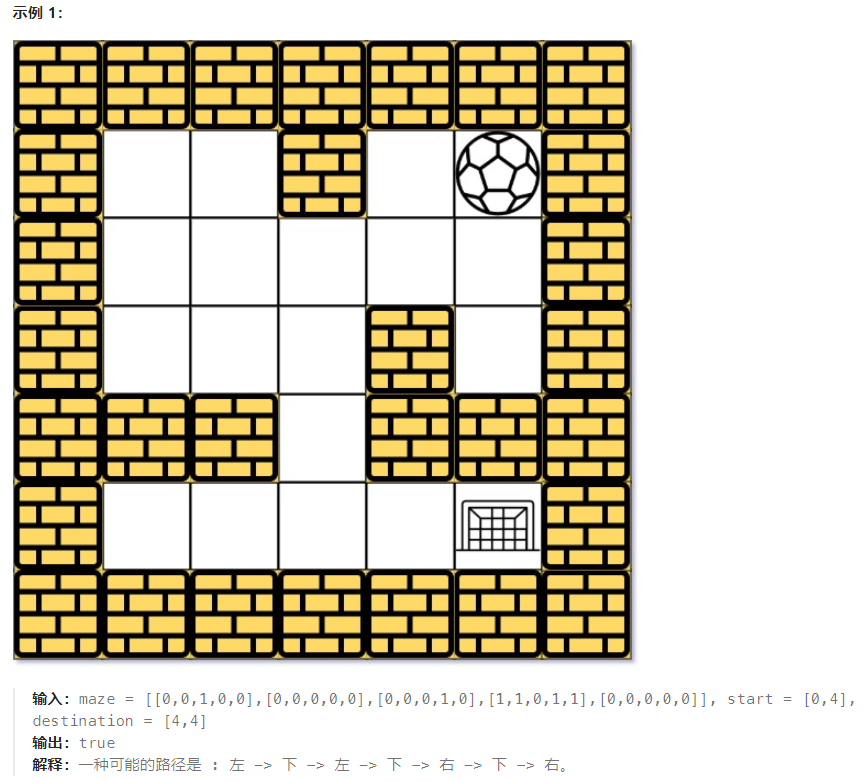
手法 1:循环队列,tail = (tail + 1) % QUEUE_LEN
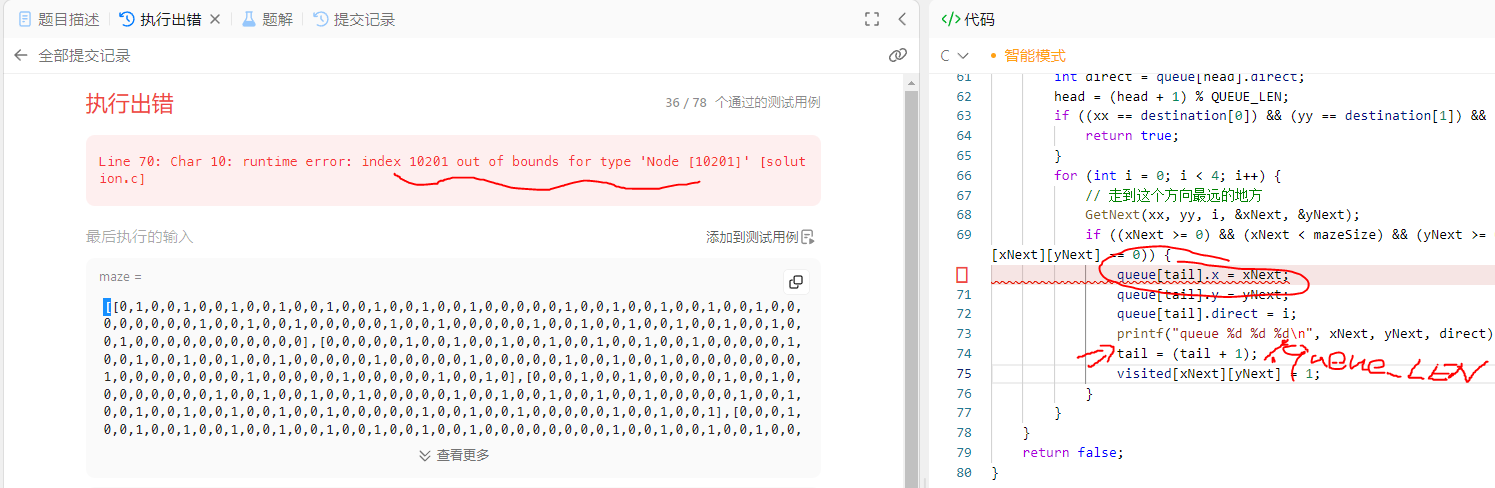
否则会产生队列溢出(数组溢出)
完整代码:
#define QUEUE_LEN (101 * 101)
#define MAX_N 101
typedef struct Node {
int x;
int y;
int direct;
} Node;
Node queue[QUEUE_LEN];
int head = 0;
int tail = 0;
int **matrix;
int m, n;
int visited[MAX_N][MAX_N];
int gDirection[4][2] = {{-1,0}, {0,1}, {1,0}, {0,-1}};
bool IsValid(int i, int j)
{
if (i < 0 || i >= m || j < 0 || j >= n) {
return false;
}
return true;
}
bool IsNextWall(int i, int j, int direct)
{
int xNext, yNext;
xNext = i + gDirection[direct][0];
yNext = j + gDirection[direct][1];
if (IsValid(xNext, yNext) == false) {
return true;
}
if (matrix[xNext][yNext] == 1) {
return true;
}
return false;
}
void GetNext(int i, int j, int direct, int *posX, int *posY)
{
int xNext, yNext;
xNext = i + gDirection[direct][0];
yNext = j + gDirection[direct][1];
// 走到这个方向最远的地方
while (IsValid(xNext, yNext) && (matrix[xNext][yNext] == 0)) {
xNext = xNext + gDirection[direct][0];
yNext = yNext + gDirection[direct][1];
}
*posX = xNext - gDirection[direct][0];
*posY = yNext - gDirection[direct][1];
}
bool BFS(int mazeSize, int *mazeColSize, int *destination)
{
int xNext = 0, yNext = 0;
while (head != tail) {
int xx = queue[head].x;
int yy = queue[head].y;
int direct = queue[head].direct;
head = (head + 1) % QUEUE_LEN;
if ((xx == destination[0]) && (yy == destination[1]) && (IsNextWall(xx, yy, direct) == true)) {
return true;
}
for (int i = 0; i < 4; i++) {
// 走到这个方向最远的地方
GetNext(xx, yy, i, &xNext, &yNext);
if ((xNext >= 0) && (xNext < mazeSize) && (yNext >= 0) && (yNext < *mazeColSize) && (visited[xNext][yNext] == 0)) {
queue[tail].x = xNext;
queue[tail].y = yNext;
queue[tail].direct = i;
printf("queue %d %d %d\n", xNext, yNext, direct);
tail = (tail + 1) % QUEUE_LEN;
visited[xNext][yNext] = 1;
}
}
}
return false;
}
bool hasPath(int **maze, int mazeSize, int *mazeColSize, int *start, int startSize, int *destination, int destinationSize)
{
matrix = maze;
m = mazeSize;
n = *mazeColSize;
memset(visited, 0, sizeof(visited));
queue[tail].x = start[0];
queue[tail].y = start[1];
visited[start[0]][start[1]] = 1;
tail = (tail + 1) % QUEUE_LEN;
return BFS(mazeSize, mazeColSize, destination);
}
int main(void)
{
int **grid = (int **)malloc(sizeof(int *));;
int mazeSize = 5;
int mazeColSize = 5;
for (int i = 0; i < 5; i++) {
grid[i] = (int *)malloc(sizeof(int) * 5);
}
grid[0][0] = 0;
grid[0][1] = 0;
grid[0][2] = 1;
grid[0][3] = 0;
grid[0][4] = 0;
grid[1][0] = 0;
grid[1][1] = 0;
grid[1][2] = 0;
grid[1][3] = 0;
grid[1][4] = 0;
grid[2][0] = 0;
grid[2][1] = 0;
grid[2][2] = 0;
grid[2][3] = 1;
grid[2][4] = 0;
grid[3][0] = 1;
grid[3][1] = 1;
grid[3][2] = 0;
grid[3][3] = 1;
grid[3][4] = 1;
grid[4][0] = 0;
grid[4][1] = 0;
grid[4][2] = 0;
grid[4][3] = 0;
grid[4][4] = 0;
int start[2] = {0, 4};
int startSize = 2;
int destination[2] = {4, 4};
int destinationSize = 2;
bool ret = hasPath(grid, mazeSize, &mazeColSize, start, startSize, destination, destinationSize);
return 0;
}
994. 腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
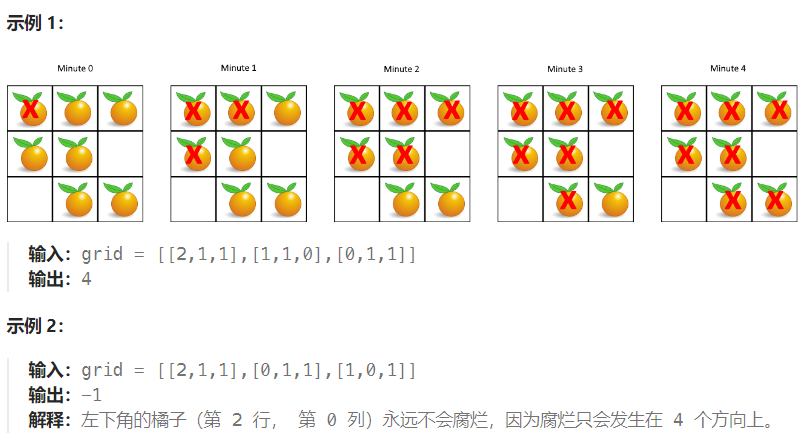
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1
#define QUEUE_LEN (101 * 101)
#define NUM_101 101
typedef struct Node {
int x;
int y;
int depth;
} Node;
int head = 0;
int tail = 0;
int gDirection[4][2] = {{-1,0}, {0,1}, {1,0}, {0,-1}};
int orangesRotting(int **grid, int gridSize, int *gridColSize)
{
int row = gridSize, col = gridColSize[0];
Node queue[NUM_101];
int head = 0, tail = 0;
int depth = 0;
int fresh = 0;
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (grid[i][j] == 2) {
queue[tail].x = i;
queue[tail].y = j;
tail = (tail + 1) % NUM_101;
} else if (grid[i][j] == 1) {
fresh++;
}
}
}
while ((head != tail) && (fresh > 0)) { // fresh用来剪枝
int size = tail - head;
while (size > 0) { // 多源BFS
int xx = queue[head].x;
int yy = queue[head].y;
head = (head + 1) % NUM_101;
size--;
for (int i = 0; i < 4; ++i) {
int xNext = xx + gDirection[i][0];
int yNext = yy + gDirection[i][1];
if (0 <= xNext && xNext < row && 0 <= yNext && yNext < col && grid[xNext][yNext] == 1) {
grid[xNext][yNext] = 2;
queue[tail].x = xNext;
queue[tail].y = yNext;
queue[tail].depth = depth;
tail = (tail + 1) % NUM_101;
fresh--;
printf("queue = %d %d \n", xNext, yNext);
}
}
}
depth = depth + 1;
printf("depth %d \n", depth);
}
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (grid[i][j] == 1) {
return -1;
}
}
}
return depth;
}
int main(void)
{
int **grid = (int **)malloc(sizeof(int *));;
int mazeSize = 3;
int mazeColSize = 3;
for (int i = 0; i < 3; i++) {
grid[i] = (int *)malloc(sizeof(int) * 3);
}
grid[0][0] = 2;
grid[0][1] = 1;
grid[0][2] = 1;
grid[1][0] = 1;
grid[1][1] = 1;
grid[1][2] = 1;
grid[2][0] = 0;
grid[2][1] = 1;
grid[2][2] = 2;
int ret = orangesRotting(grid, mazeSize, &mazeColSize);
printf("ret = %d", ret);
return 0;
}
463. 岛屿的周长
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
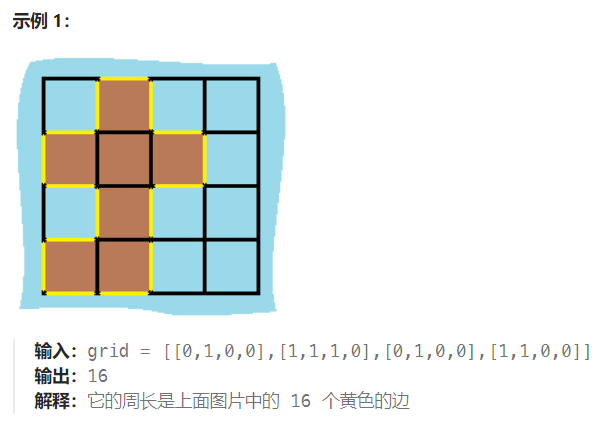
手法1:用BFS不好解,因为是存“非法”的值到queue里
对于一个陆地格子的每条边,它被算作岛屿的周长当且仅当这条边为网格的边界或者相邻的另一个格子为水域。 因此,我们可以遍历每个陆地格子,看其四个方向是否为边界或者水域,如果是,将这条边的贡献(即 1)加入答案 ans 中即可。
int gDirection[4][2] = { {-1,0}, {0,1}, {1,0}, {0,-1} };
int islandPerimeter(int **grid, int gridSize, int *gridColSize)
{
int n = gridSize, m = gridColSize[0];
int ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] == 1) {
int cnt = 0;
for (int k = 0; k < 4; ++k) {
int xNext = i + gDirection[k][0];
int yNext = j + gDirection[k][1];
if (xNext < 0 || xNext >= n || yNext < 0 || yNext >= m || (grid[xNext][yNext] == 0)) {
cnt += 1;
}
}
ans += cnt;
}
}
}
return ans;
}





 本文深入探讨了广度优先搜索(BFS)的应用技巧,通过具体示例如200.岛屿数量、286.墙与门及752.打开转盘锁等题目,详细解析了BFS在寻找最短路径、遍历图结构和解决复杂问题中的作用。
本文深入探讨了广度优先搜索(BFS)的应用技巧,通过具体示例如200.岛屿数量、286.墙与门及752.打开转盘锁等题目,详细解析了BFS在寻找最短路径、遍历图结构和解决复杂问题中的作用。
















 7196
7196

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








