什么是第一名的含金量呢?他的RMSE直接领先最前沿方法一个数量级!
文章中多次提到了 forward model / operator,于是我进行了一些查阅,给出个人的一些理解:
作为 forward model 实际上指的就是输入求解输出的求解(推演)过程,与之相对应的就是反演,又叫逆问题求解。在本文中指的就是将稀疏视图CT求解成正常剂量CT的过程。
数据一致性:是指要求预测结果与标签一致、或者说处于同一分布。
1. 介绍
关于深度学习在重建领域是否可以得到可靠稳定的结果一直有所争议,作者表示不服,于是他参加这个比赛去证明数据驱动的恢复工作流可以实现(接近)精确的图像恢复。
作者的方法是基于如下:
High reconstruction accuracy is only possible when the forward model is explicitly incor-
porated into the reconstruction mapping, e.g., by an iterative promotion of data-consistent
solutions.只有当正向模型被明确地结合到重建映射中时,高重建精度才是可能的,例如,通过数据一致解决方案的迭代提升。
作者贡献如下:
-
鉴于精确的正演模型未知,作者对潜在的扇束几何形状进行数据驱动的估计。这是通过以类似深度学习的方式(即,通过具有反向传播/自动微分的梯度下降)将通用的参数化扇束算子拟合到所提供的正弦图图像对来实现的。作者希望这种方法可以在几何校正和前向算子(forward operator)校正的情况下进一步使用。特别是,我们目前正在探索一种基于正弦图一致性条件的无监督识别策略。
-
我们提出了一个概念简单,但功能强大的深度学习工作流,它将后处理UNet [RFB15]变成了一个迭代重建方案。从技术角度来看,其大部分设计组件之前已在文献中报道过。然而,整个策略似乎是新颖的,并且在几个方面不同于更常见的展开网络,包括:(a)我们使用预先训练的UNet作为计算主干;(b)数据一致性受到L2梯度步骤的启发,但是利用滤波反投影而不是常规伴随投影。我们认为,所提出的策略也将用于其他逆问题,因为它在均方根误差(RMSE)方面优于其他最先进的数据驱动方法,如学习原始对偶算法一个数量级。
2. 方法
在本节中,作者将简要概述他们的方法,以及一些设计选择的动机。
Step1 Data-Driven Geometry Identification(数据驱动的几何识别)
重建流水线的第一步是从提供的训练数据中学习未知的正向算子。断层扇形束测量的连续版本基于计算线积分:
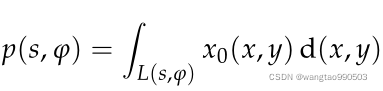
其中是未知图像,
表示扇束坐标中的一条线,即
是扇束旋转角度,
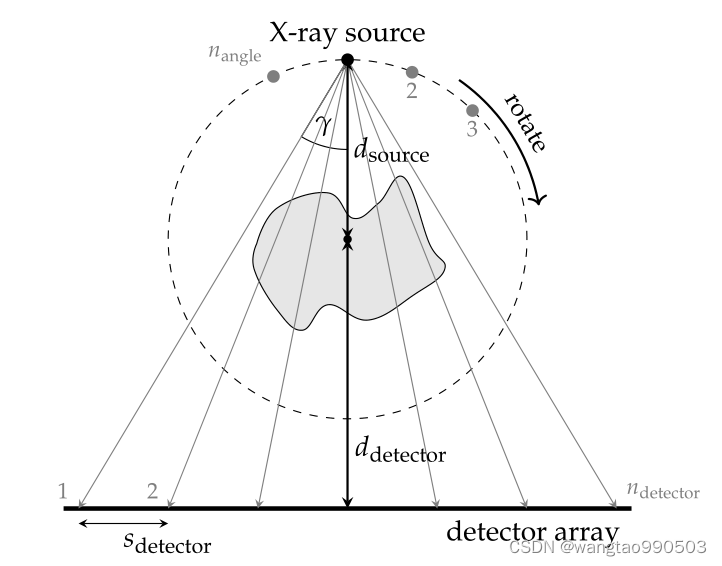
用于编码 the 传感器位置。在理想情况下,扇束模型由下列几何参数确定(见图1):
- X射线源到原点的距离;
- 探测器阵列到原点的距离;
- 探测器的元件数量;
- 探测器元件沿阵列的间距;
- 扇束旋转角度的数量;
- 旋转角度的离散列表,是
个离散的0-2pi之间的值。
这里假设积分只沿有限条线测量,由m := *
确定。在AAPM DL-稀疏视图挑战中,所得到的前向算子是严重不适定的,因为只获得了几个扇束旋转角度的测量值。此外,几何设置不向挑战参与者公开,只知道进行了扇形束测量。
我们





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2031
2031










