【机器学习-17】-矩阵运算-向量化实现

【机器学习-17】-矩阵运算-向量化实现

以下内容涵盖AI分类、神经元模型、神经网络实现及矩阵运算即神经网络计算时向量化的关键知识点：

---

1. AI分类体系（图1）

• 核心概念：
• ANI（人工狭义智能）：专精单一任务（如智能音箱、自动驾驶）。
• AGI（人工通用智能）：具备人类全能力（尚未实现）。
• 应用场景：
• ANI：农业、工厂自动化、搜索引擎等。
• AGI：理论探索阶段。

---

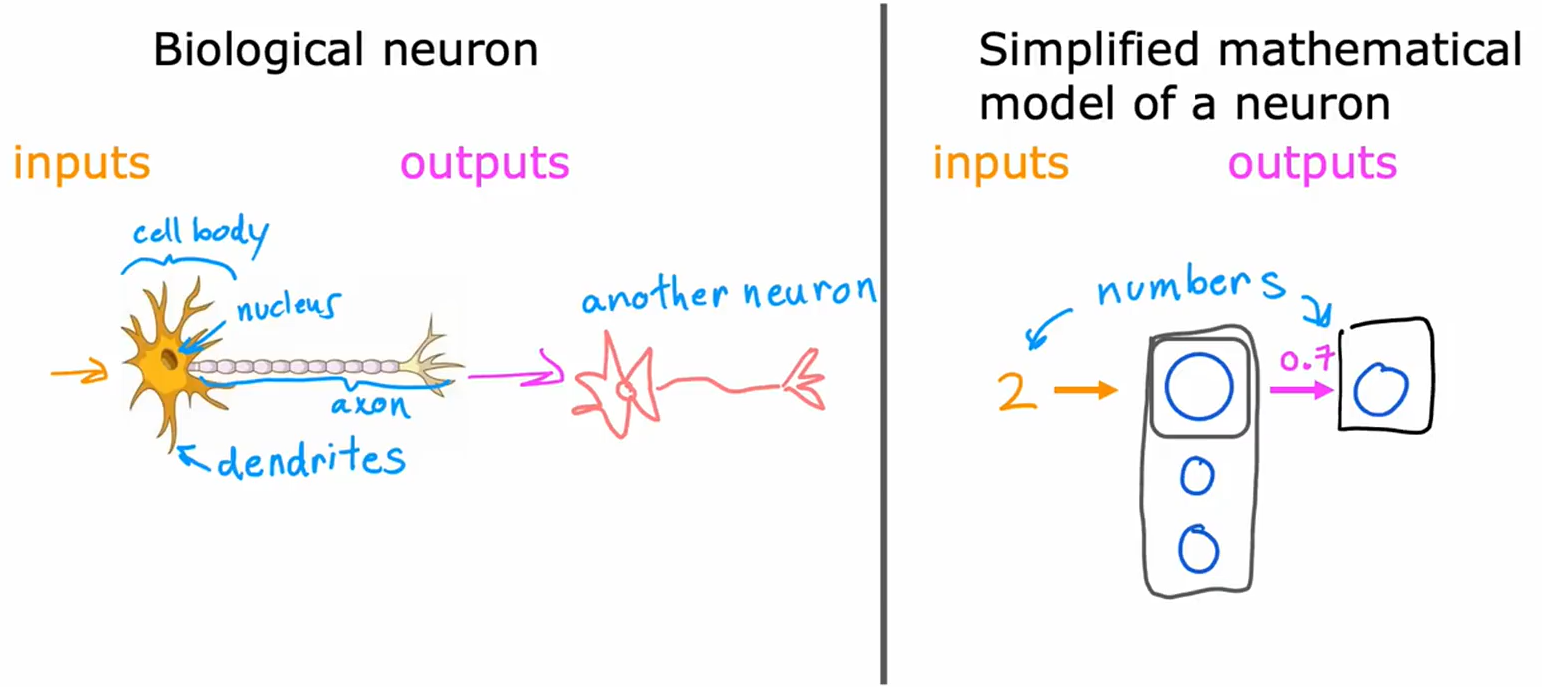
2. 神经元模型对比（图2-3）

生物神经元 vs. 数学模型

生物神经元（图2）	数学模型（图2-3）
- 细胞体、树突（输入）	- 输入向量（如 [0.7, 2]）
- 轴突（输出）	- 激活函数（如 sigmoid）
- 复杂化学信号传递	- 线性加权和 + 非线性变换

关键结论（图3）

• 当前神经网络仅简化模拟生物神经元，人脑工作机制仍不明确。

---

3. 神经网络实现：循环 vs. 向量化（图4, 8）

代码对比与优化

循环实现（图4左）	向量化实现（图4右, 图8）
- 逐元素计算（for循环）	- 矩阵乘法（np.matmul）
- 效率低	- 并行计算，速度快
- 代码冗长	- 简洁，接近数学公式

示例（图8）

• 输入：A_in = [200, 17]
• 权重：W = [[1, -3, 5], [2, 4, -6]]
• 偏置：b = [-1, 1, 2]
• 输出计算：

Z = np.matmul(A_in, W) + b  # 结果为 [165, -531, 900]
A_out = g(Z)                # 激活后输出如 [1, 0, 1]

---

4. 矩阵乘法规则（图5-7）

核心规则

1. 维度匹配（图6）：
   • 若 A 是 m×n，W 需为 n×p，结果 Z 为 m×p。
   • 例如（图5）：A^T (3×2) × W (2×4) → Z (3×4)。

2. 计算步骤（图5-6）：
   • 结果矩阵每个元素是行向量与列向量的点积。
   • 示例计算（图5）：
   ◦ Z[0,0] = 1*3 + 2*4 = 11
   ◦ Z[2,1] = 0.1*5 + 0.2*6 = 1.7

3. NumPy实现（图7）：

   Z = np.matmul(A.T, W)  # 或 A.T @ W
   

---

5. 综合解题思路

题目类型：实现神经网络前向传播

1. 输入处理：将输入数据转为NumPy数组（如 [200, 17]）。
2. 参数定义：按层初始化权重 W 和偏置 b（注意维度匹配）。
3. 计算步骤：
   • 使用向量化乘法计算每层输出：Z = A_prev @ W + b。
   • 应用激活函数：A = g(Z)。
4. 优化：优先选择向量化实现（避免循环）。

示例代码（结合图8）

import numpy as np

def dense_layer(A_in, W, b, activation):
    Z = np.matmul(A_in, W) + b
    return activation(Z)

# 示例参数
W = np.array([[1, -3, 5], [2, 4, -6]])
b = np.array([-1, 1, 2])
A_in = np.array([[200, 17]])
A_out = dense_layer(A_in, W, b, sigmoid)  # 假设sigmoid已定义

---

总结

• 理论到实践：从AI分类到神经元模型，最终落地为矩阵运算和代码实现。
• 关键技巧：理解维度匹配、掌握向量化运算、合理选择激活函数。
• 延伸思考：对比不同激活函数（如ReLU）对结果的影响。

如需进一步探讨具体图片中的细节，可指定图片编号！