【机器学习03】神经网络的反向传播 梯度函数求解
神经网络的反向传播(Backpropagation)是一种通过计算损失函数梯度来调整网络权重的算法,是训练深度学习模型的核心方法。以下是其关键步骤和原理的清晰总结:
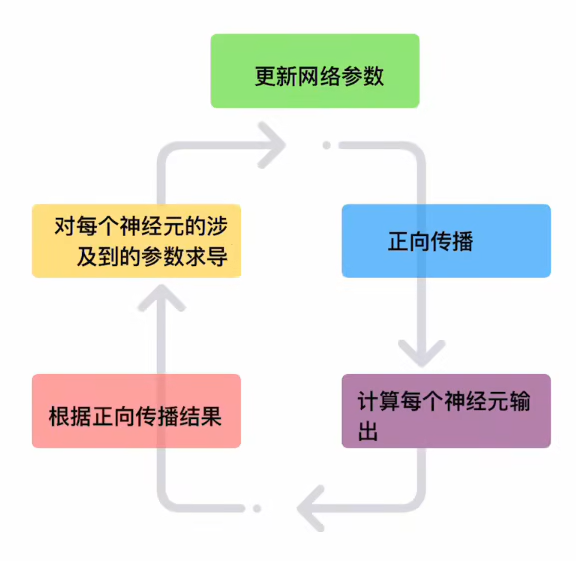
1. 网络结构
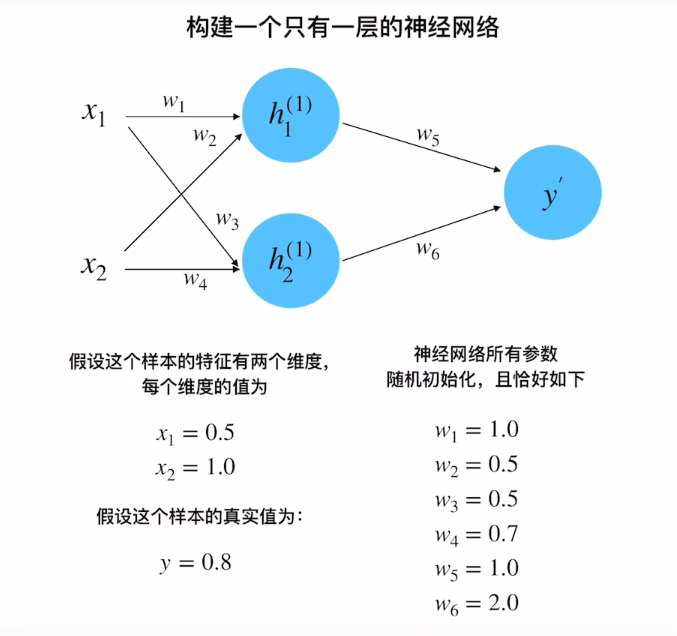
- 单隐藏层神经网络:输入层 → 隐藏层(2个神经元) → 输出层
- 参数初始化:
- 权重:
w₁=1.0,w₂=0.5,w₃=0.5,w₄=0.7,w₅=1.0,w₆=2.0 - 输入:
x₁=0.5,x₂=1.0 - 真实值:
y=0.8 - 学习率:
η=0.1
- 权重:
2. 正向传播过程
隐藏层计算
h 1 ( 1 ) = w 1 x 1 + w 2 x 2 = 1.0 × 0.5 + 0.5 × 1.0 = 1.0 h 2 ( 1 ) = w 3 x 1 + w 4 x 2 = 0.5 × 0.5 + 0.7 × 1.0 = 0.95 \begin{aligned} h_1^{(1)} &= w_1x_1 + w_2x_2 = 1.0×0.5 + 0.5×1.0 = 1.0 \\ h_2^{(1)} &= w_3x_1 + w_4x_2 = 0.5×0.5 + 0.7×1.0 = 0.95 \end{aligned} h1(1)h2(1)=w1x1+w2x2=1.0×0.5+0.5×1.0=1.0=w3x1+w4x2=0.5×0.5+0.7×1.0=0.95
输出层计算
y ′ = w 5 h 1 ( 1 ) + w 6 h 2 ( 1 ) = 1.0 × 1.0 + 2.0 × 0.95 = 2.9 y' = w_5h_1^{(1)} + w_6h_2^{(1)} = 1.0×1.0 + 2.0×0.95 = 2.9 y′=w5h1(1)+w6h2(1)=1.0×1.0+2.0×0.95=2.9
损失计算
采用均方误差:
δ
=
1
2
(
y
−
y
′
)
2
=
0.5
×
(
0.8
−
2.9
)
2
=
2.205
δ = \frac{1}{2}(y-y')^2 = 0.5×(0.8-2.9)^2 = 2.205
δ=21(y−y′)2=0.5×(0.8−2.9)2=2.205
3. 反向传播过程
输出层梯度
∂ δ ∂ y ′ = ∂ ( 1 2 ( y − y ′ ) 2 ) ∂ y ′ = ( y − y ′ ) ∗ ( − 1 ) = ( 0.8 − 2.9 ) ∗ ( − 1 ) = 2.1 \frac{∂δ}{∂y'} =\frac{∂(\frac{1}{2}(y-y')^2)}{∂y'} = (y-y ')*(-1)= (0.8-2.9)*(-1) = 2.1 ∂y′∂δ=∂y′∂(21(y−y′)2)=(y−y′)∗(−1)=(0.8−2.9)∗(−1)=2.1
权重更新(以w₅为例)
-
计算梯度:
w₅的梯度
∂ δ ∂ w 5 = ∂ δ ∂ y ′ ⋅ ∂ y ′ ∂ w 5 = 2.1 × 1.0 = 2.1 \frac{∂δ}{∂w_5} = \frac{∂δ}{∂y'}·\frac{∂y'}{∂w_5} = 2.1×1.0 = 2.1 ∂w5∂δ=∂y′∂δ⋅∂w5∂y′=2.1×1.0=2.1w 5 u p d a t e = w 5 − η ⋅ ∂ δ ∂ w 5 = 1.0 − 0.1 × 2.1 = 0.79 w_5^{update} = w_5 - η·\frac{∂δ}{∂w_5} = 1.0 - 0.1×2.1 = 0.79 w5update=w5−η⋅∂w5∂δ=1.0−0.1×2.1=0.79
其中
∂ y ′ ∂ w 5 = ∂ ∂ w 5 ( w 5 h 1 ( 1 ) + w 6 h 2 ( 1 ) ) \frac{∂y'}{∂w_5} = \frac{∂}{∂w_5}(w_5h_1^{(1)} + w_6h_2^{(1)}) ∂w5∂y′=∂w5∂(w5h1(1)+w6h2(1))
= h 1 ( 1 ) + 0 = h_1^{(1)} +0 =h1(1)+0
= 1.0 = 1.0 =1.0
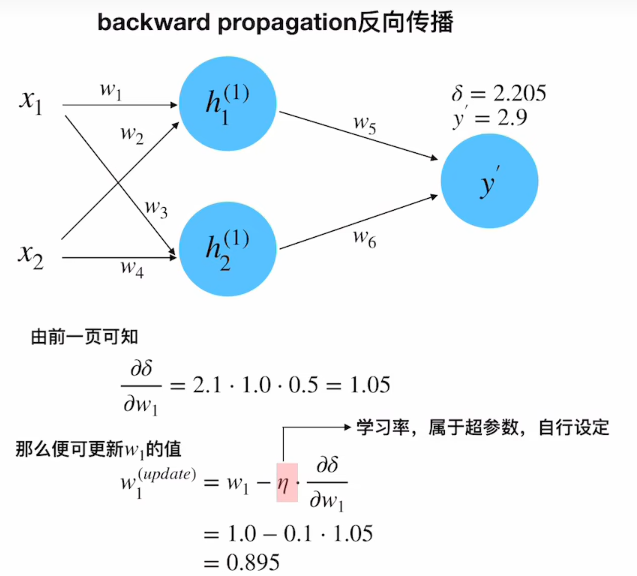
同理 w 1 w_1 w1的梯度为
∂ δ ∂ w 1 = ∂ δ ∂ y ′ ⋅ ∂ y ′ ∂ h 1 ( 1 ) ⋅ ∂ h 1 ( 1 ) ∂ w 1 = 2.1 × 1.0 × 0.5 = 1.05 \frac{\partial \delta}{\partial w_1} = \frac{\partial \delta}{\partial y'} \cdot \frac{\partial y'}{\partial h_1^{(1)}} \cdot \frac{\partial h_1^{(1)}}{\partial w_1} = 2.1 \times 1.0 \times 0.5 = 1.05 ∂w1∂δ=∂y′∂δ⋅∂h1(1)∂y′⋅∂w1∂h1(1)=2.1×1.0×0.5=1.05
w
1
update
=
w
1
−
η
⋅
∂
δ
∂
w
1
=
1.0
−
0.1
×
1.05
=
0.895
w_1^{\text{update}} = w_1 - \eta \cdot \frac{\partial \delta}{\partial w_1} = 1.0 - 0.1 \times 1.05 = 0.895
w1update=w1−η⋅∂w1∂δ=1.0−0.1×1.05=0.895
其中
∂
y
′
∂
h
1
(
1
)
=
w
5
=
1.0
\frac{\partial y'}{\partial h_1^{(1)}} = w_5 = 1.0
∂h1(1)∂y′=w5=1.0
∂
h
1
(
1
)
∂
w
1
=
x
1
=
0.5
\frac{\partial h_1^{(1)}}{\partial w_1} = x_1 = 0.5
∂w1∂h1(1)=x1=0.5
4. 关键公式总结
| 计算步骤 | 公式 |
|---|---|
| 神经元输出 | h = ∑ w i x i h = \sum w_ix_i h=∑wixi |
| 损失函数 | δ = 1 2 ( y − y ′ ) 2 δ = \frac{1}{2}(y-y')^2 δ=21(y−y′)2 |
| 输出层梯度 | ∂ δ ∂ y ′ = y ′ − y \frac{∂δ}{∂y'} = y'-y ∂y′∂δ=y′−y |
| 权重梯度 | ∂ δ ∂ w i = ∂ δ ∂ y ′ ⋅ ∂ h i ∂ w i \frac{∂δ}{∂w_i} = \frac{∂δ}{∂y'}·\frac{∂h_i}{∂w_i} ∂wi∂δ=∂y′∂δ⋅∂wi∂hi |
| 参数更新 | w u p d a t e = w − η ⋅ ∂ δ ∂ w w_{update} = w - η·\frac{∂δ}{∂w} wupdate=w−η⋅∂w∂δ |
以下是图片演示
第一次正向传播
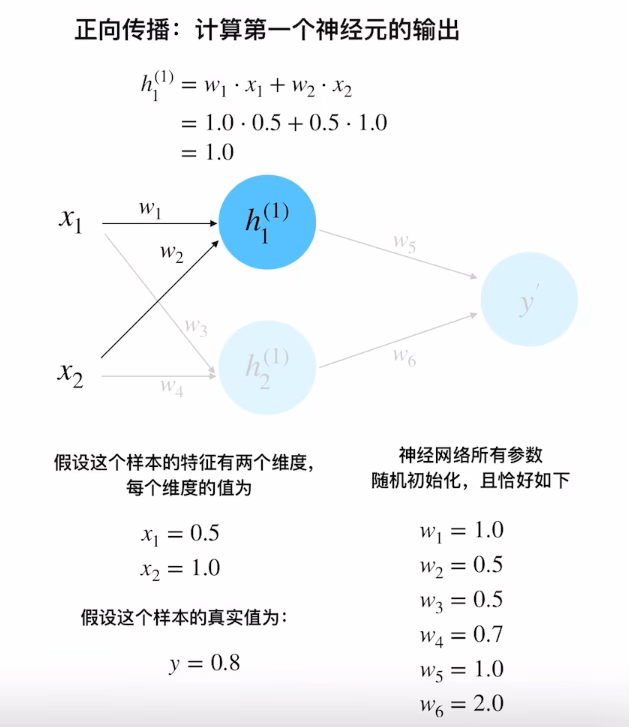
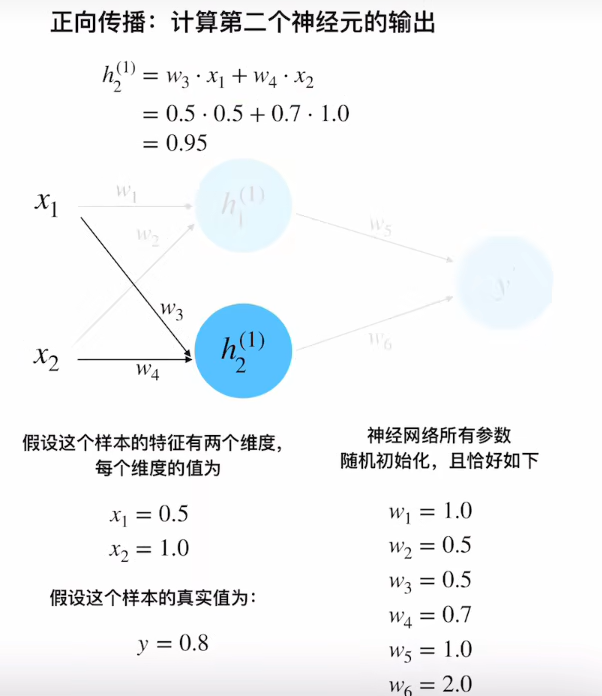
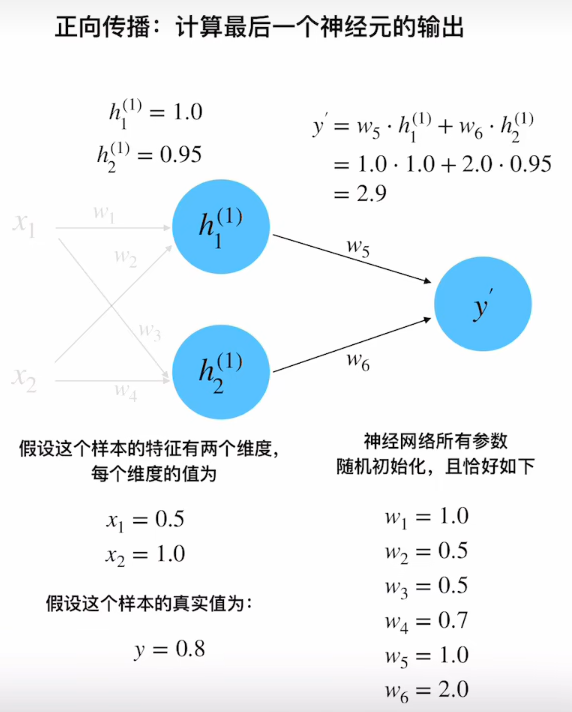
正向传播完成

反向传播
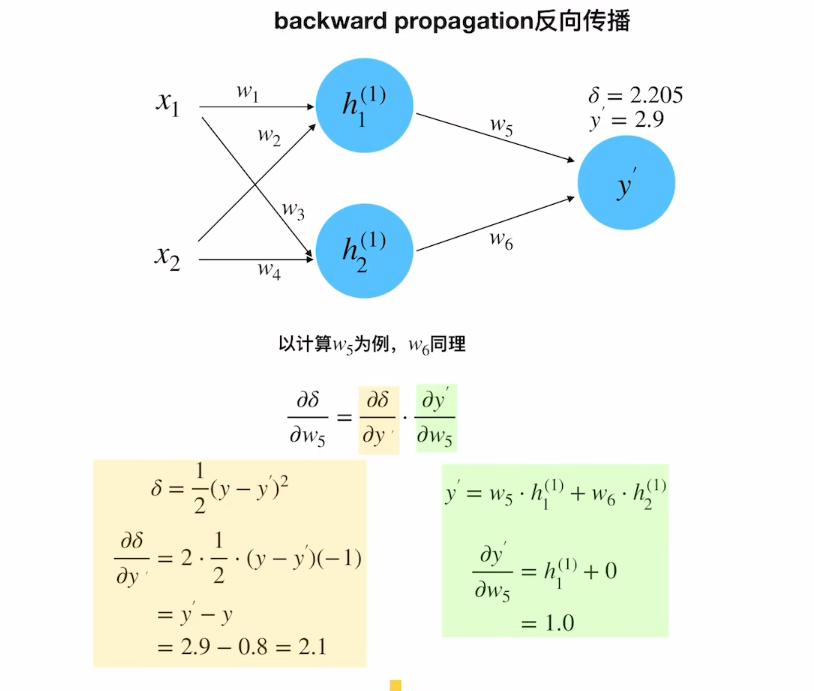
w
5
(
u
p
d
a
t
e
)
w_5^{(update)}
w5(update)
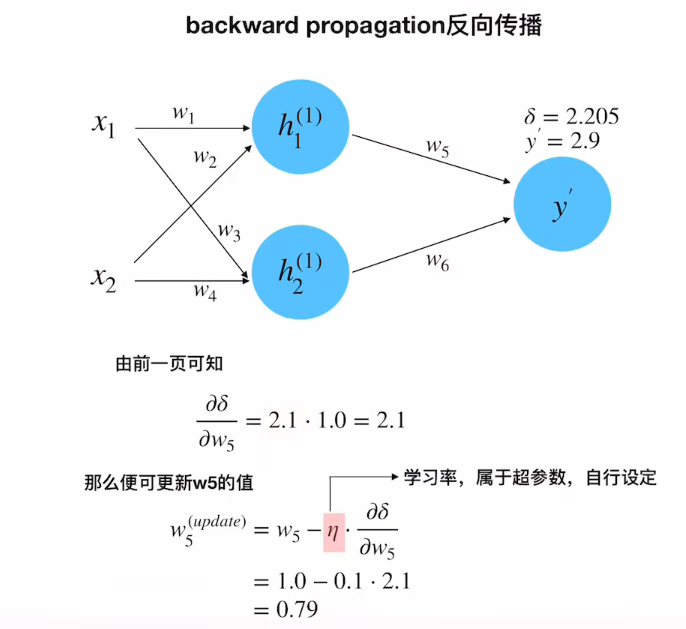
w
1
(
u
p
d
a
t
e
)
w_1^{(update)}
w1(update)
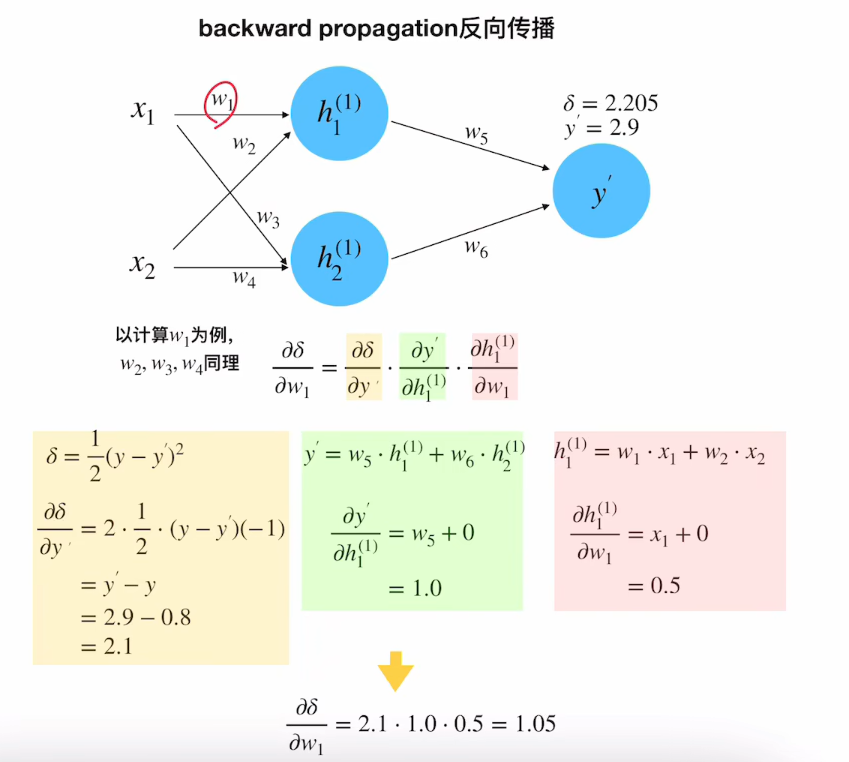
所有权重w
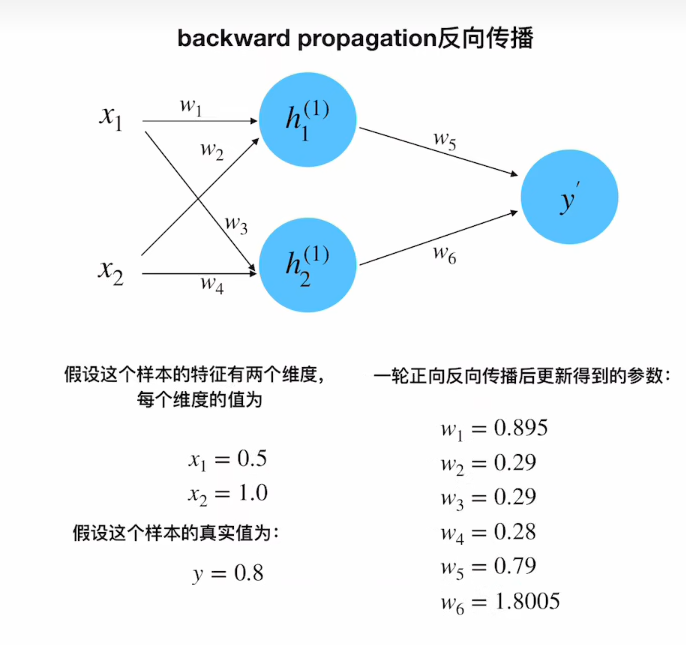
第二次正向传播
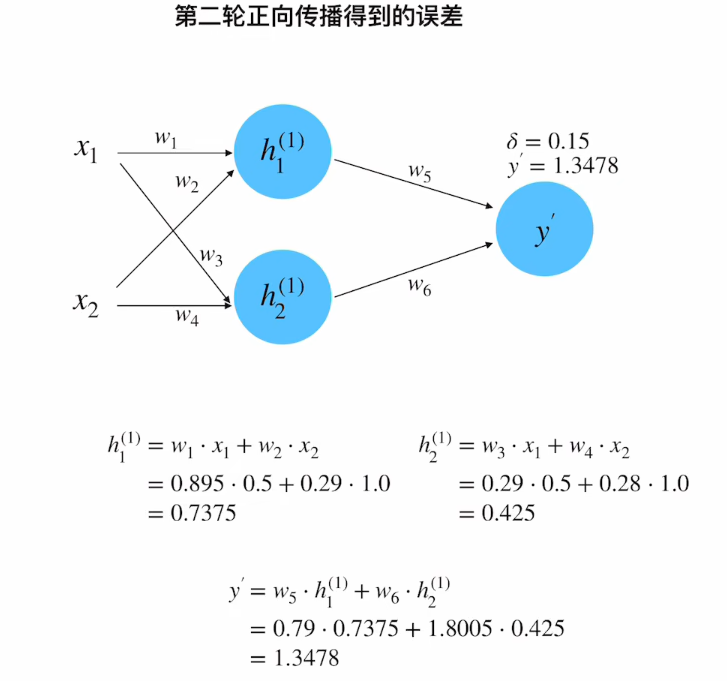
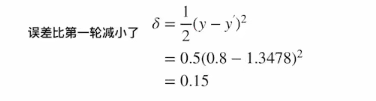
至此,便完成了所有参数的更新;
结合前面的图文讲解,整个前向传播和反向传播,应该已经非常清楚了
有几点要再说明下:
1.这个case重点是在讲解清楚,正向传播和方向传播,为了举例说明中的计算方便,没有给每个神经元加上激活函数;
2.在实际使用的神经网络中,每个神经元在上文计算的基础上,会再通过一个激活函数,才能得到最后的值;
3.然后求导的时候,要再结合激活函数的形式求导;但整个流程没有任何区别;
4.网上很多内容会说,反向传播就是链式求导,然后就没了;我相信在这个教程里,一定已经把这个过程完全讲清楚了;
5.神经网络里,面试还会问,什么是梯度消失梯度爆炸,以及为什么,和如何解决;这些知识点如果大家感兴趣,也可以留言,以后安排;
图片来自 望舒同学 学习






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








