本文深入讲解了DP算法的应用，包括最长公共子序列问题的高效解决方法、编辑距离问题的难点剖析及优化技巧，以及粉刷匠问题的复杂状态转移与优化。
前言
最近去外地集训，应该不太会有时间写笔记了。
其实最后一道题应该是一道神仙DP，但是可惜空间太小我写不下。
P1439 【模板】最长公共子序列
解析：
按照正常的最长公共子序列的O(n2)做法，毫无疑问会TLE。
然后我们观察到一个性质，
对于递增序列A和A的一个排列B：A与B的公共子序列等价于B的上升子序列。
首先证明A与B的公共子序列一定是B的上升子序列。这个没什么好说的，因为A一定递增，所以A的子序列一定递增，于是A与B的公共子序列一定递增。
然后证明B的上升子序列一定是A与B的公共子序列。这是因为，对于在B中的两个数字x<y，且x在y的前面，x、y在A中一定出现，且相对位置关系一定不变（因为在A中，大数在小数的后面）。用数学归纳法可以证明，对于任意长度的B的上升序列都是成立的。
于是，A与B的最长公共子序列就等于B的最长上升子序列。
在题目中，我们习惯B为递增序列：
接下来考虑如何将B转化为递增序列。
比如：
A={3，1，2，5，4}
B={4，5，3，1，2}
我们可以直接将B数组中的4替换为1，同时将A数组中的4替换为1。
将B数组中的5替换为2，同时将A数组中的5替换为2。
以此类推。
然后我们可以使用O(nlogn)的单调栈优化最长上升子序列轻松AC这一道题目了！
诶？单调栈优化最长上升子序列不太好写呀…找找自己原来的代码里有没有吧…
最后只找到了一份单调栈优化最长不上升子序列的代码…
但是不要着急，因为A数组元素互不相同，所以最长上升子序列=最长不下降子序列了。再将A数组全部添负号，那么求出的最长不上升子序列长度就等于原本的最长不下降子序列长度了。
代码如下：
#include<iostream>
#include<algorithm>
using namespace std;
int&merge(int f[],int l,int r,int x) {//在一个不升序列中找到第一个<=x的数字
if(l==r) return f[l];
int mid=l+r>>1;
if(f[mid]<x) return merge(f,l,mid,x);
else return merge(f,mid+1,r,x);
}
int a[100005],b[100005];
int g[100005],f[100005];
int main() {
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
cin>>b[i];
for(int i=1;i<=n;i++)
g[b[i]]=i;
for(int i=1;i<=n;i++)
a[i]=g[a[i]];
for(int i=1;i<=n;i++)
b[i]=i;
int cnt=1;
for(int i=1;i<=n;i++)
a[i]=-a[i];
f[cnt]=a[1];
for(int i=2;i<=n;i++)
if(a[i]<=f[cnt]) f[++cnt]=a[i];
else merge(f,1,cnt,a[i])=a[i];
cout<<cnt;
return 0;
}
P2758 编辑距离
题目分析：
裸的DP题目，状态的设计与转移都非常简单：
设f[i][j]表示前i位的a字符串已经变成了前j位的b字符串所需要的最小操作次数。
转移时考虑a[i]是否等于b[j]：
如果相等，那么f[i][j]=f[i-1][j-1]，显然要匹配。
如果不相等，那么就必须得改变a字符串，f[i][j]=min{f[i-1][j],f[i][j-1],f[i-1][j-1]}+1,分别对应着删除a[i]；在a[i]与a[i+1]之间插入一个字符c，使得c=b[j]；直接将a[i]改为b[j]。
于是产生了如下代码：
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
char a[2005],b[2005];
int f[2005][2005];
int main() {
cin>>&a[1]>>&b[1];
int n=strlen(&a[1]),m=strlen(&b[1]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(a[i]==b[j])
f[i][j]=f[i-1][j-1];
else
f[i][j]=min({f[i-1][j],f[i][j-1],f[i-1][j-1]})+1;
cout<<f[n][m];
return 0;
}
交上去我们会发现WA掉了。
于是开始考虑这道题目的难点：
初始化
首先想到所有位置的f应该赋为1e9，如果一个状态始终未被更新过，那么也不应该转移向其他位置。（尽管这个初始化在实现中是不必要的。）
其次想到f[0][0]=0。（如果不给所有位置赋值1e9，并且定义全局变量的话，这个初值也可以不写）
接下来想到一个比较难想的初始化：
f[i][0]=i，f[0][j]=j
这两个初始化语义是显然的，第一个：a字符串中前i个字符匹配b字符串中前0个字符需要的操作数显然为i（把a中前i个字符都删了）
第二个：a字符串前0个字符匹配b字符串前j个字符需要的操作数显然为j（只能在a字符串中添加上b字符串的前j个字符）
AC代码如下：
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
char a[2005],b[2005];
int f[2005][2005];
int main() {
cin>>&a[1]>>&b[1];
int n=strlen(&a[1]),m=strlen(&b[1]);
for(int i=1;i<=n;i++)
f[i][0]=i;
for(int j=1;j<=m;j++)
f[0][j]=j;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(a[i]==b[j])
f[i][j]=f[i-1][j-1];
else
f[i][j]=min({f[i-1][j],f[i][j-1],f[i-1][j-1]})+1;
cout<<f[n][m];
return 0;
}
P4158 [SCOI2009]粉刷匠
虽然同样是省选题目，但确实比前几天的数字序列容易不少。
首先，错误涂颜色和不涂颜色在结果上是一样的，对答案产生0的贡献，所以可以认为所有不涂的都是涂了错误的颜色，可以减一点状态。
注意到同一块木板不能重复粉刷，也就是不可以反悔。
暴力DP：
设f[i][j][k][0/1]表示使用前i次机会，在第j个木板上涂了前k块格子，第k块格子涂了红色(0)/蓝色(1)，正确粉刷的颜色数量。这里注意只计算第j块木板上的颜色数量，不统计之前的。（好像题解区也有人统计之前的数量，也是可以做的。）
首先可以想到一个暴力转移：
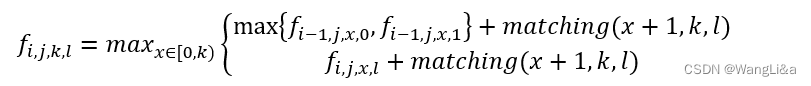
函数matching(l,r,c)]表示在第j块木板上，粉刷[l,r]区间为颜色c，可以产生的对于答案的贡献。matching函数可以前缀和优化。
这个公式的语义是：
对于上面第一行的那一种情况，我们从[1,x]继承原来的结果中的最大值。再花费一次粉刷的机会，将[x+1,k]粉刷上颜色l，计算可以得到的贡献。
对于公式第二行的那一种情况，我们原本使用第i次机会粉刷到了第x块木板，现在继续使用第i次机会粉刷到了第k块木板，计算可以得到的贡献。（这时候要求使用第i次机会的颜色和现在粉刷的颜色相同，所以只能从相同颜色的状态转移过来）
最后还需要计算在第几个木板上使用了几次机会，设计g[i][j]表示前i块木板上使用了总计j次机会获得的最大贡献，显然是一个背包，直接暴力转移即可。
代码如下：
#include<iostream>
#include<algorithm>
using namespace std;
bool a[55][55];
int pre[55][55][2];
int f[2505][55][55][2];
int g[55][2505];
int matching(int x,int l,int r,bool c) {
return pre[x][r][c]-pre[x][l-1][c];
}
int main(){
int n,m,t;
cin>>n>>m>>t;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) {
char ch;
cin>>ch;
a[i][j]=ch=='1'?true:false;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
pre[i][j][0]=pre[i][j-1][0]+!a[i][j],
pre[i][j][1]=pre[i][j-1][1]+a[i][j];
for(int i=1;i<=t;i++)
for(int j=1;j<=n;j++) {
for(int k=1;k<=m;k++)
for(int x=0;x<k;x++)
f[i][j][k][0]=max(
f[i][j][k][0],
max({f[i-1][j][x][0],f[i-1][j][x][1],f[i][j][x][0]})+matching(j,x+1,k,0)
),
f[i][j][k][1]=max(
f[i][j][k][1],
max({f[i-1][j][x][0],f[i-1][j][x][1],f[i][j][x][1]})+matching(j,x+1,k,1)
);
}
// cout<<matching(1,1,m,1)<<endl;
// for(int i=1;i<=m;i++)
// cout<<i<<": "<<f[2][2][i][0]<<" "<<f[2][2][i][1]<<endl;
// cout<<endl;
int maxx=0;
//g[i][j] 表示用前i次机会粉刷前j个木板的最大匹配
for(int i=1;i<=n;i++) //木板
for(int j=1;j<=t;j++) //机会
for(int k=0;k<=j;k++) //木板
maxx=max(maxx,g[i][j]=max(g[i][j],g[i-1][j-k]+max(f[k][i][m][0],f[k][i][m][1])));
// for(int i=1;i<=n;i++,cout<<endl)
// for(int j=1;j<=t;j++)
// cout<<g[i][j]<<' ';
cout<<maxx;
return 0;
}
算法复杂度=状态数×转移复杂度=O(t·j3)，算法不够优秀，不能通过该题，即使开了O2也会TLE一个点。
转移的优化
可以考虑最小增量法，即如果小的转移可以合并成为大的转移，那么在转移的过程中就没有必要枚举大的转移，只需要枚举小的转移即可，这样需要转移具有可加性。
于是转移方程产生了变化：
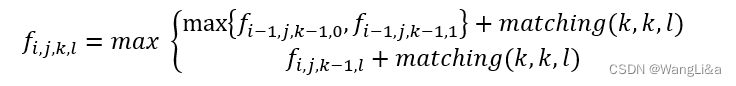
转移复杂度降为O(1)。总复杂度降为O(t·j2)，开了O2可以通过该题。
背包DP的部分不变。
代码如下：
#include<iostream>
#include<algorithm>
using namespace std;
bool a[55][55];
int pre[55][55][2];
int f[2505][55][55][2];
int g[55][2505];
int matching(int x,int l,int r,bool c) {
return pre[x][r][c]-pre[x][l-1][c];
}
int main() {
int n,m,t;
cin>>n>>m>>t;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++) {
char ch;
cin>>ch;
a[i][j]=ch=='1'?true:false;
}
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
pre[i][j][0]=pre[i][j-1][0]+!a[i][j],
pre[i][j][1]=pre[i][j-1][1]+a[i][j];
for(int i=1; i<=t; i++)
for(int j=1; j<=n; j++)
for(int k=1; k<=m; k++)
f[i][j][k][0]=max(
f[i][j][k][0],
max({f[i-1][j][k-1][0],f[i-1][j][k-1][1],f[i][j][k-1][0]})+(int)(a[j][k]==0)
),
f[i][j][k][1]=max(
f[i][j][k][1],
max({f[i-1][j][k-1][0],f[i-1][j][k-1][1],f[i][j][k-1][1]})+(int)(a[j][k]==1)
);
int maxx=0;
for(int i=1; i<=n; i++) //木板
for(int j=1; j<=t; j++) //机会
for(int k=0; k<=j; k++) //木板
maxx=max(maxx,g[i][j]=max(g[i][j],g[i-1][j-k]+max(f[k][i][m][0],f[k][i][m][1])));
cout<<maxx;
return 0;
}
后记
于是皆大欢喜。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
