涉及到动画,有很多东西是绕不开的,比如前面说的Matrix,当然还有今天要说的插值器和估值器
1、插值器
说到插值器你可能会感觉陌生,但是如果我告诉你Interpolator,你一定不会陌生,不管是普通的ViewAnimation、ObjectAnimator,ValueAnimator,使用过程中,都需要用到它,插值器就是用来控制动画执行的变化速率的。当然也可以叫加速器。
1-1、android开发中常见插值器

上面这张图就是Android中系统已经帮我们定义好的插值器实现类,
所有的插值器都是实现了Interpolator接口,而Interpolator接口继承自TimeInterpolator。
public interface TimeInterpolator {
/**
* Maps a value representing the elapsed fraction of an animation to a value that represents
* the interpolated fraction. This interpolated value is then multiplied by the change in
* value of an animation to derive the animated value at the current elapsed animation time.
*
* @param input A value between 0 and 1.0 indicating our current point
* in the animation where 0 represents the start and 1.0 represents
* the end
* @return The interpolation value. This value can be more than 1.0 for
* interpolators which overshoot their targets, or less than 0 for
* interpolators that undershoot their targets.
*/
float getInterpolation(float input);
}
TimeInterpolator 接口只有一个方法getInterpolation(float input);,这个方法会在调度时间内返回从0~1变化值。所以我们变化不同的动画插值器,实际上就是在该方法内使用不同的曲线算法,不断的返回一个趋近于物理规律的曲线时刻点的变化值。
下面简单介绍下系统提供的插值器:
1-1-1、 AccelerateDecelerateInterpolator 先加速、后减速效果插值器
- 核心代码
public class AccelerateDecelerateInterpolator extends BaseInterpolator
implements NativeInterpolator {
...//省略部分方法
public float getInterpolation(float input) {
return (float)(Math.cos((input + 1) * Math.PI) / 2.0f) + 0.5f;
}
}
1-1-2、 LinearInterpolator 匀速插值器
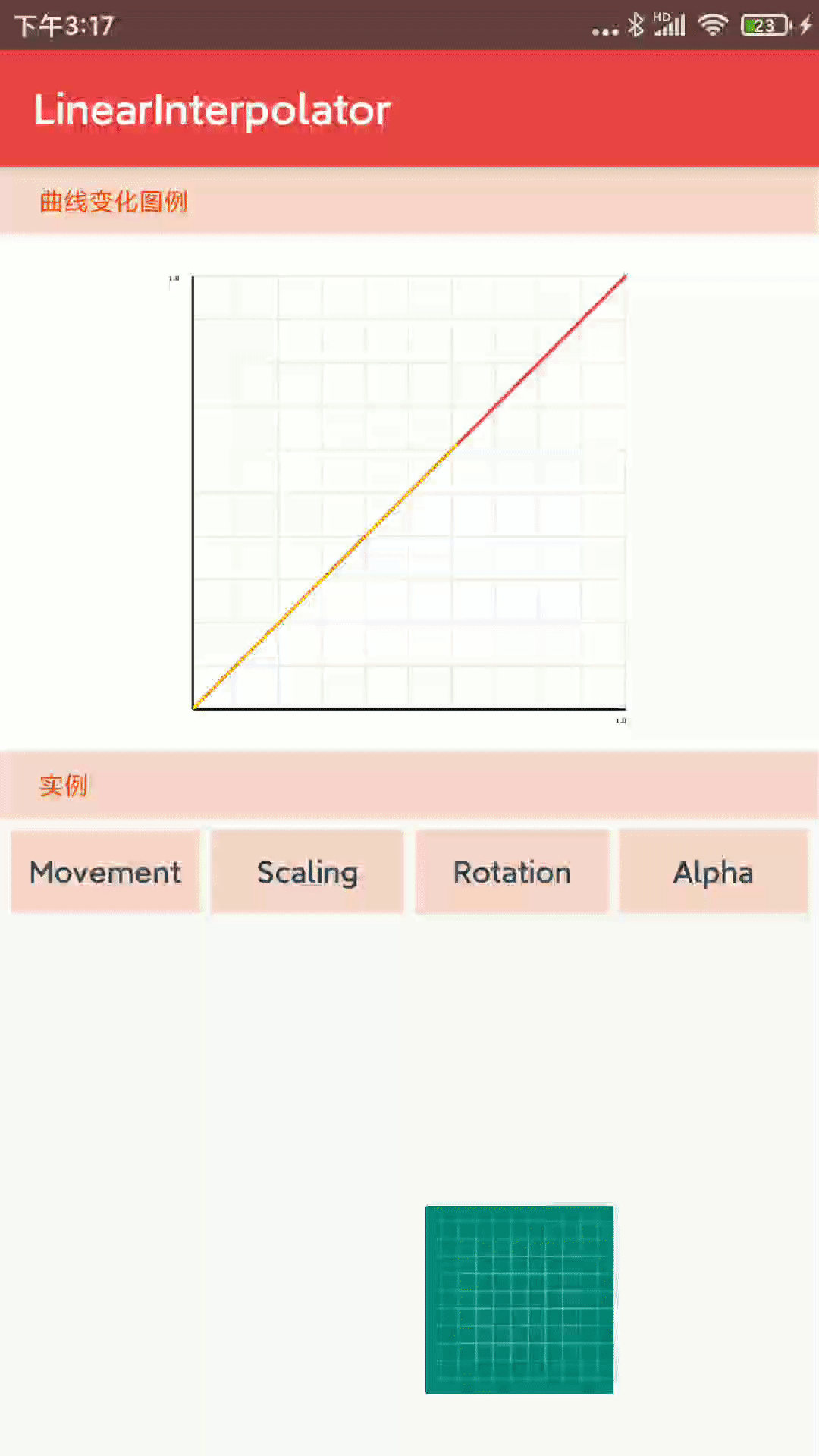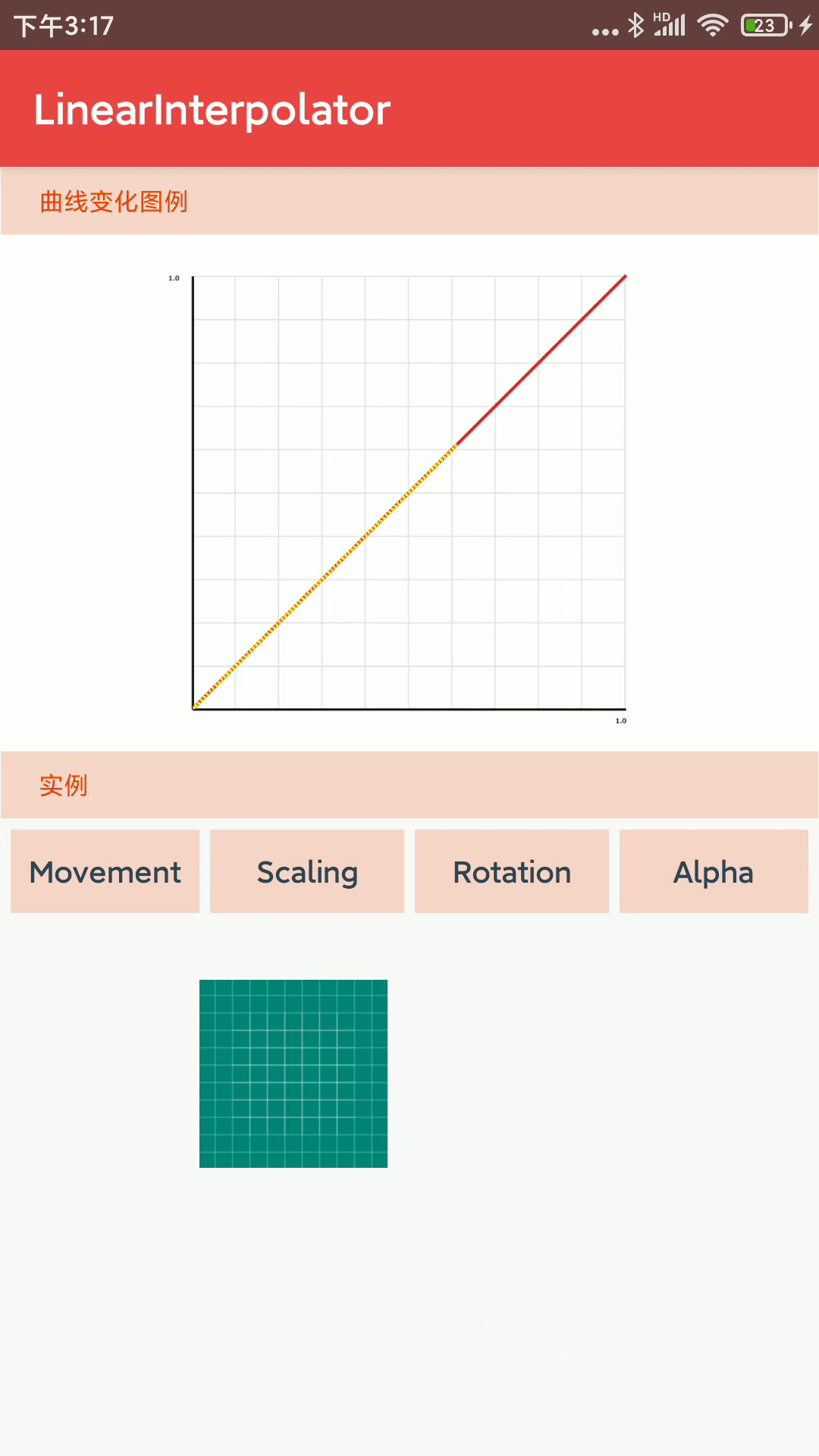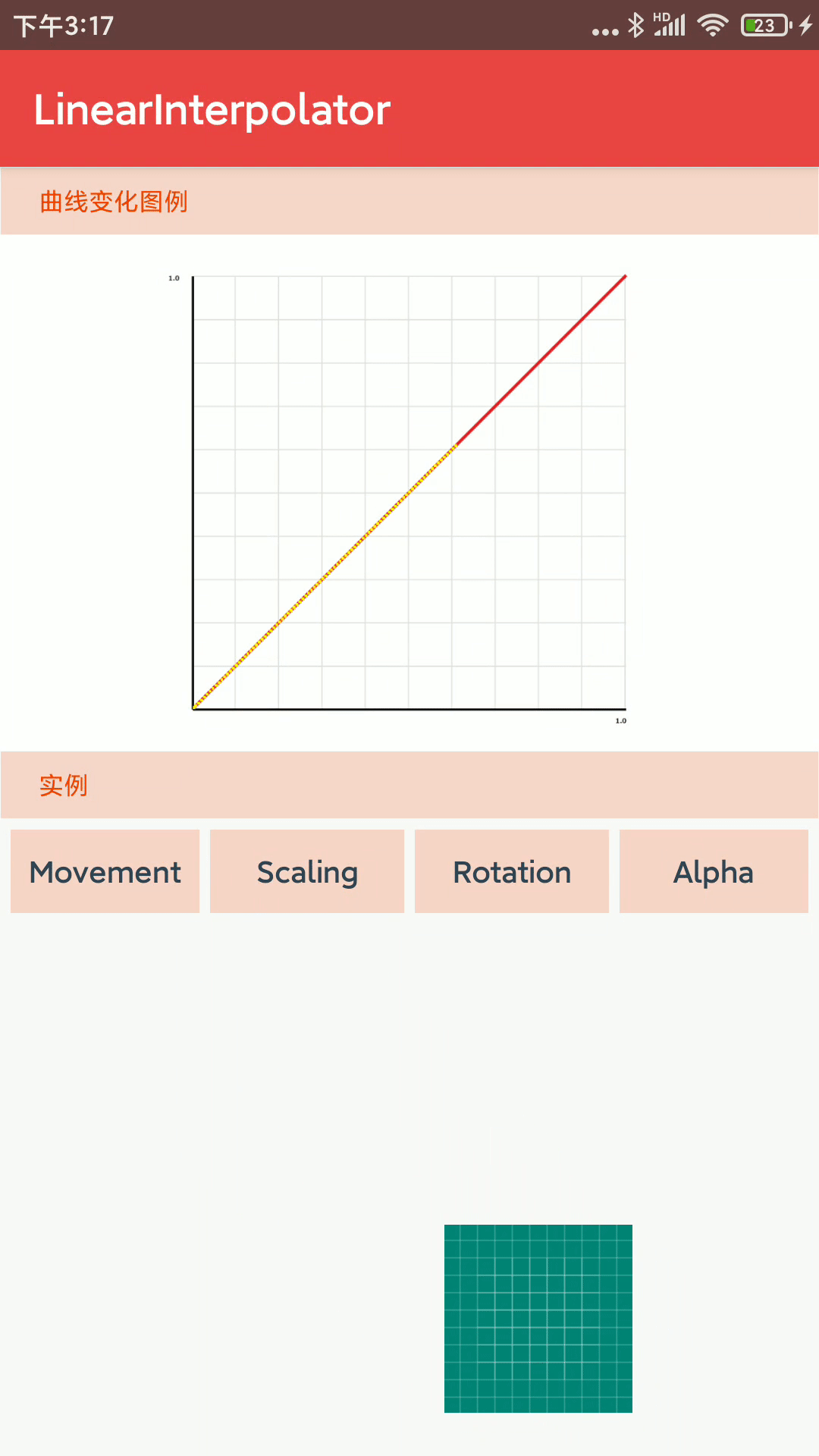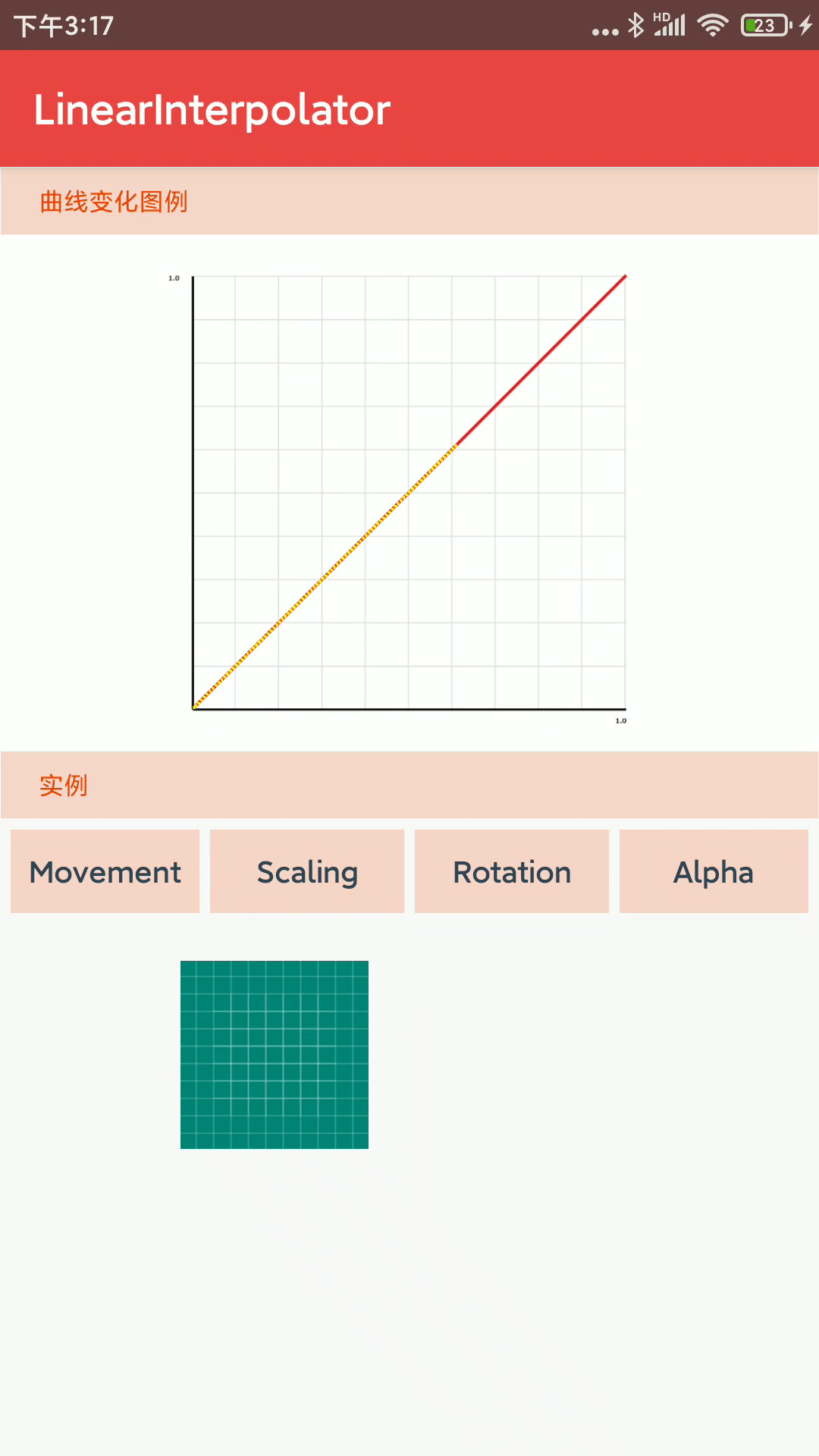
后面由于篇幅原因和gif制作比较耗时,所以只针对比较难理解的集中新增gif
- 核心代码:
public class LinearInterpolator extends BaseInterpolator implements NativeInterpolator {
...//省略部分方法
//输入多少返回多少,匀速变化
public float getInterpolation(float input) {
return input;
}
}
1-1-3、 DecelerateInterpolator 减速插值器
- 核心代码:
public class DecelerateInterpolator extends BaseInterpolator implements NativeInterpolator {
...//省略部分方法
public float getInterpolation(float input) {
float result;
if (mFactor == 1.0f) {
result = (float)(1.0f - (1.0f - input) * (1.0f - input));
} else {
result = (float)(1.0f - Math.pow((1.0f - input), 2 * mFactor));
}
return result;
}
private float mFactor = 1.0f;
}
1-1-3、 AccelerateInterpolator 加速插值器
- 核心代码:
public class AccelerateInterpolator extends BaseInterpolator implements NativeInterpolator {
...//省略部分方法
public AccelerateInterpolator(float factor) {
mFactor = factor;
mDoubleFactor = 2 * mFactor;
}
public float getInterpolation(float input) {
if (mFactor == 1.0f) {
return input * input;
} else {
return (float)Math.pow(input, mDoubleFactor);
}
}
}
1-1-4、 AnticipateInterpolator 先沿着反向运动一段距离,之后加速沿着正方向运行,类似于打羽毛球的时候挥杆效果,先向后挥动,之后加速击出。
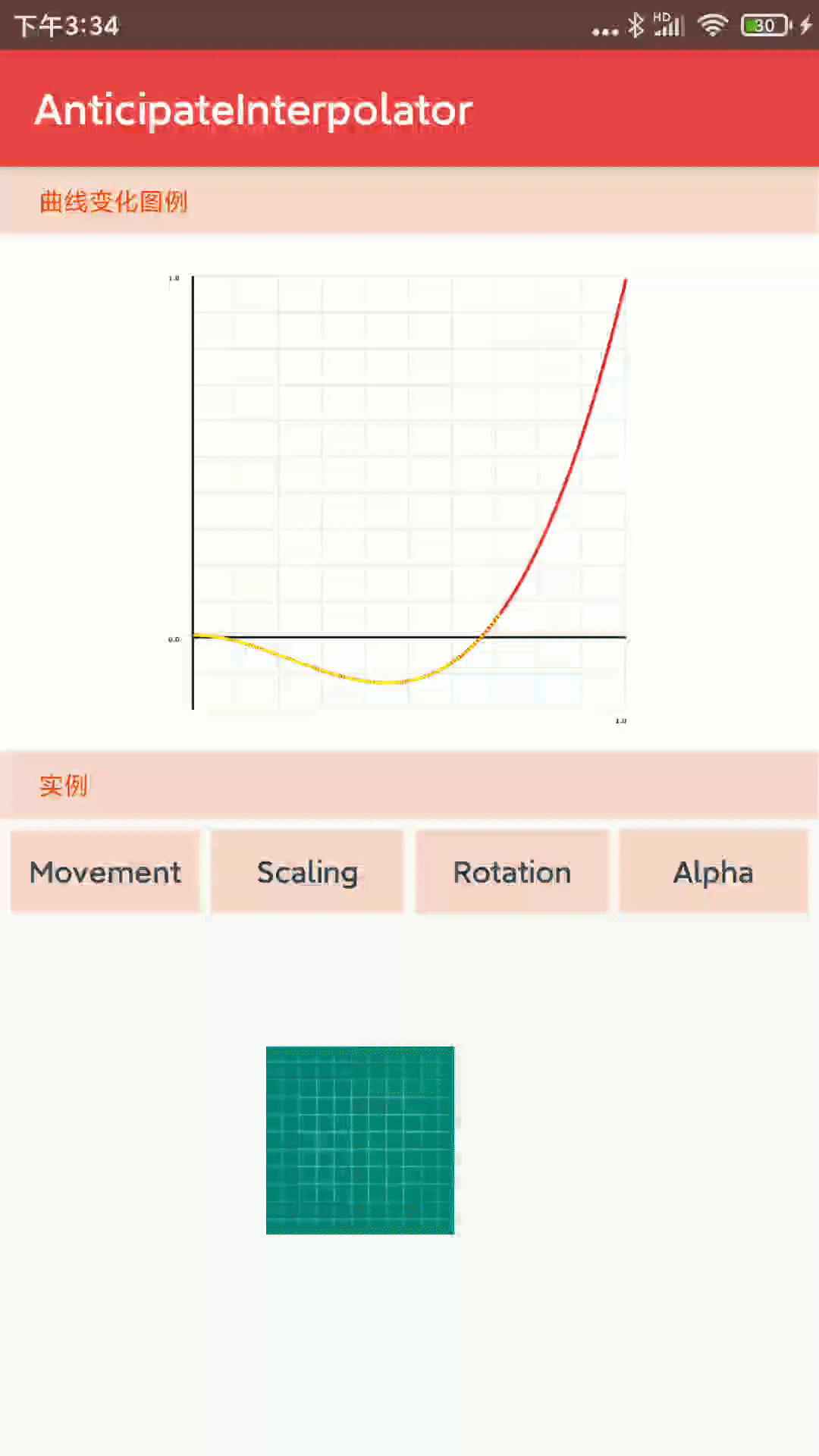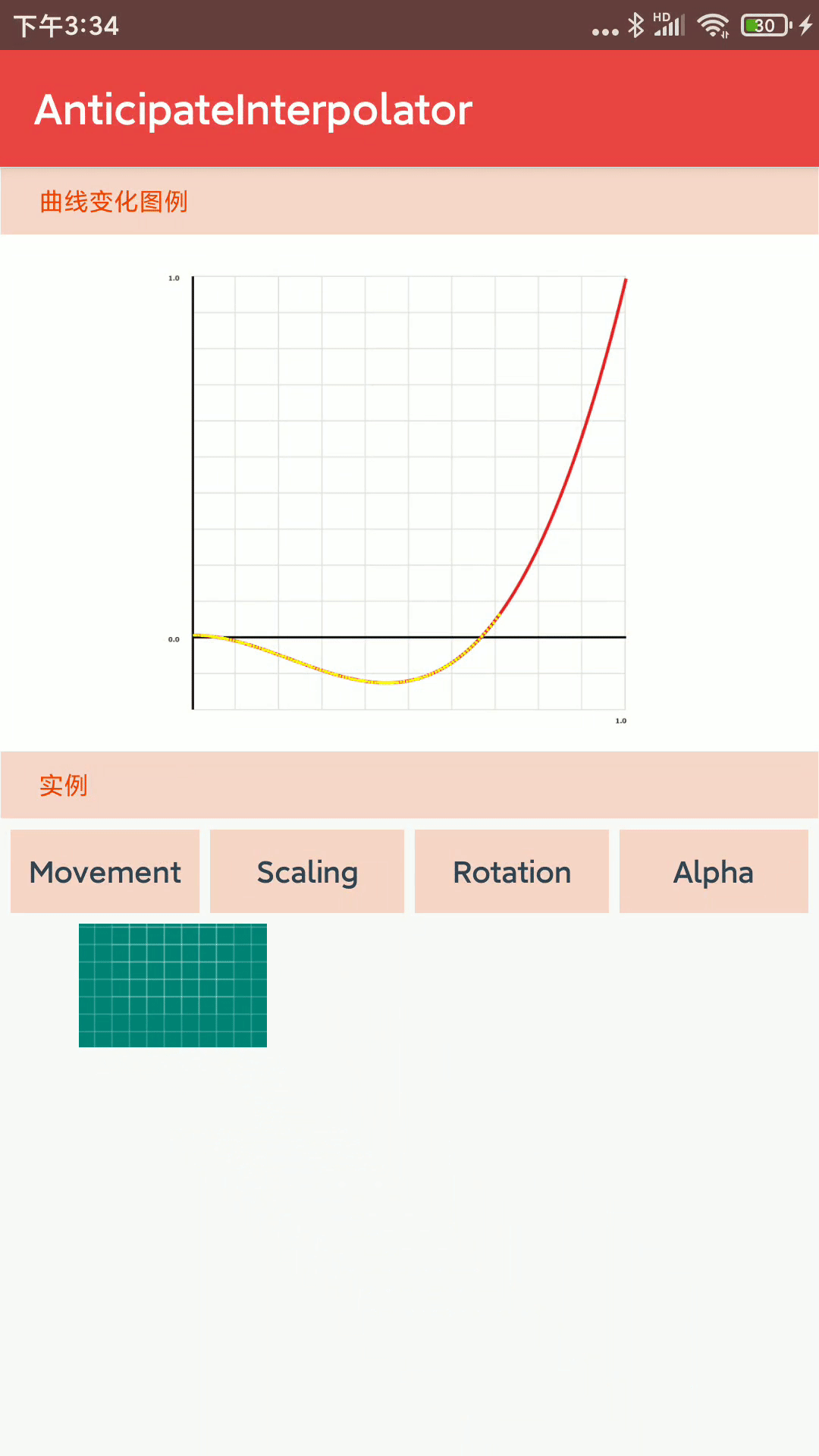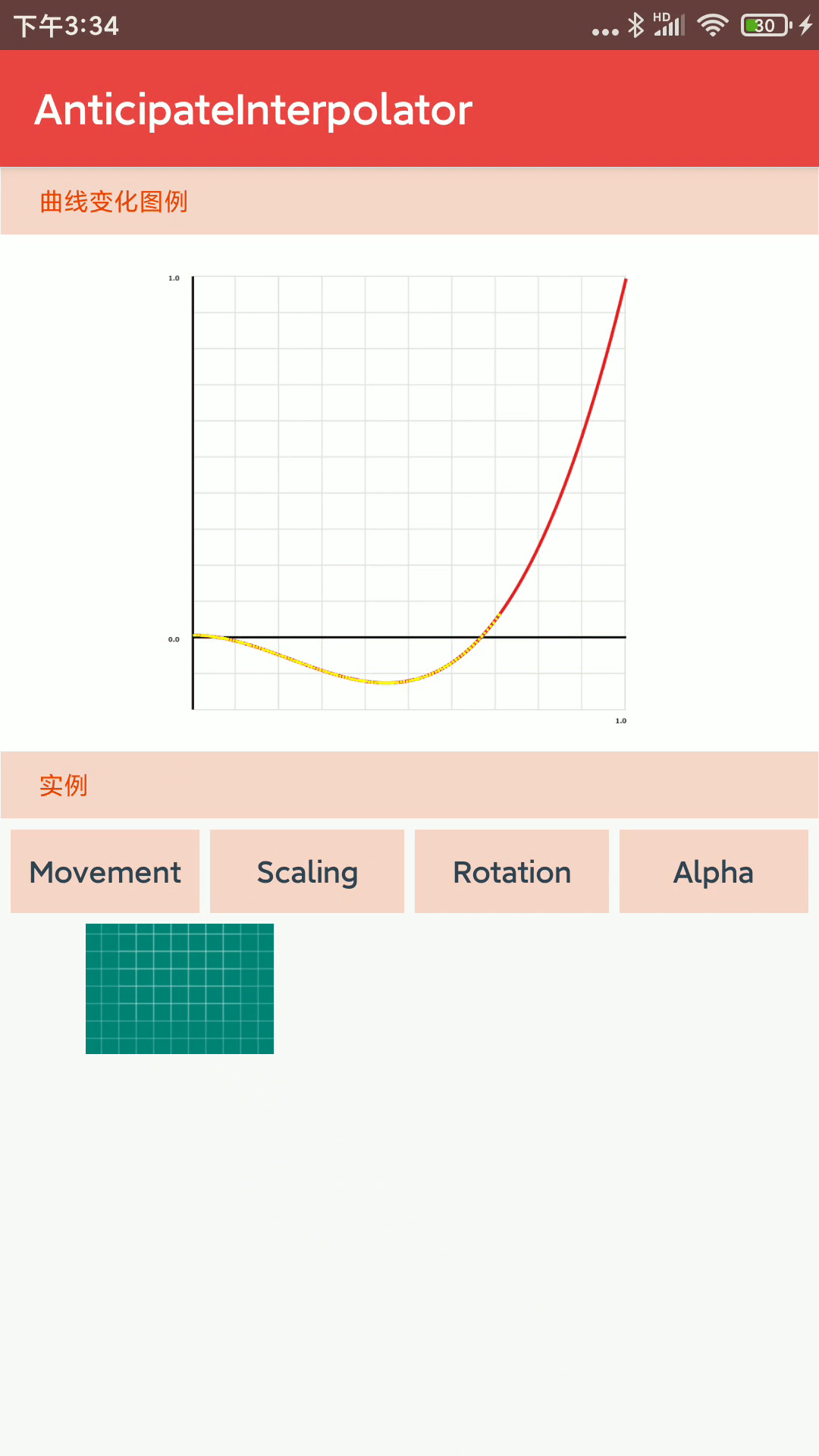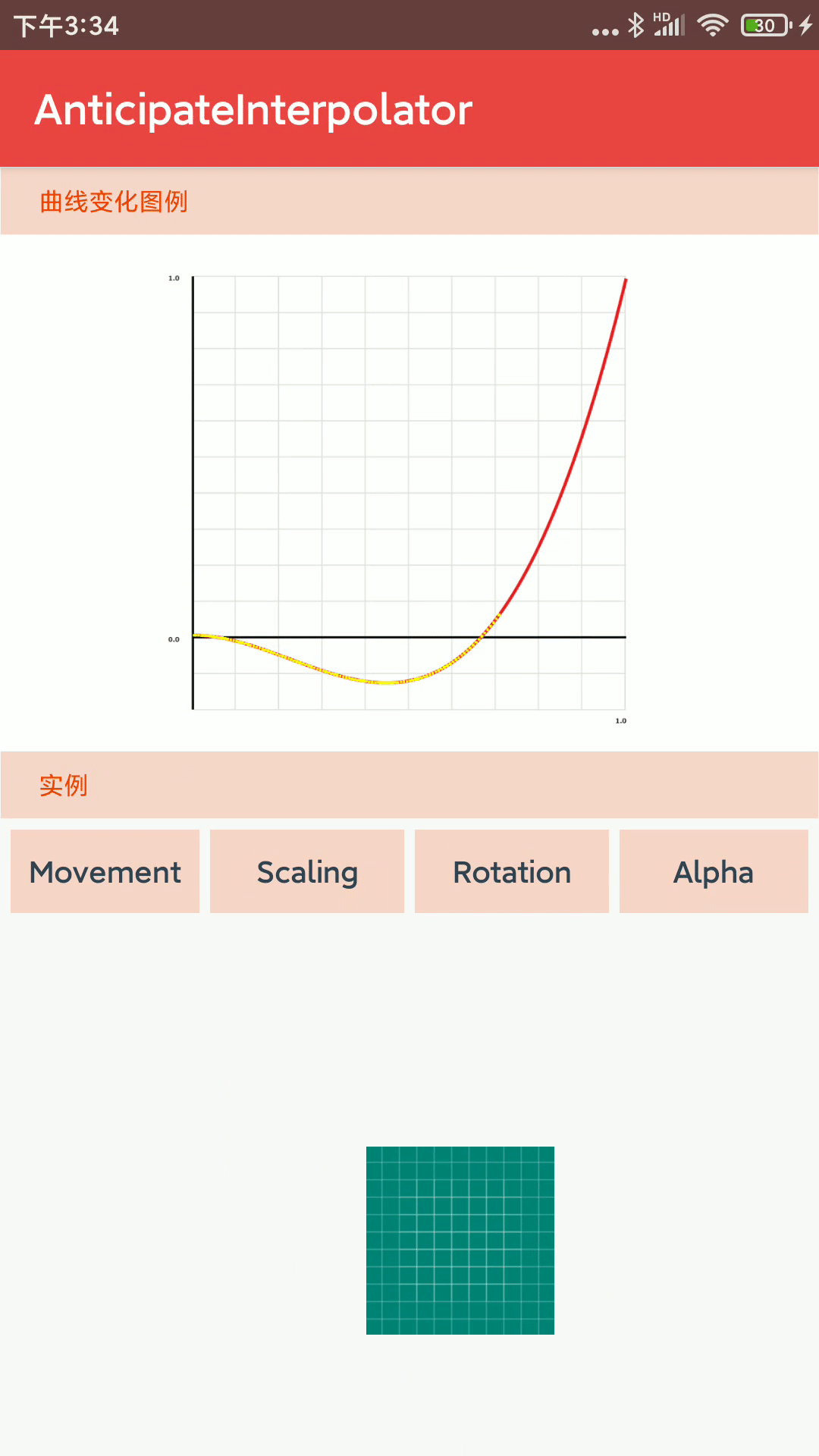
- 核心代码:
public class AnticipateInterpolator extends BaseInterpolator implements NativeInterpolator {
private final float mTension;
...//省略部分方法
public AnticipateInterpolator() {
mTension = 2.0f;
}
public float getInterpolation(float t) {
// a(t) = t * t * ((tension + 1) * t - tension)
return t * t * ((mTension + 1) * t - mTension);
}
}
1-1-5、 AnticipateOvershootInterpolator 先反向运动一段距离,之后加速运动,在减速并超过临界点在运动一段距离。
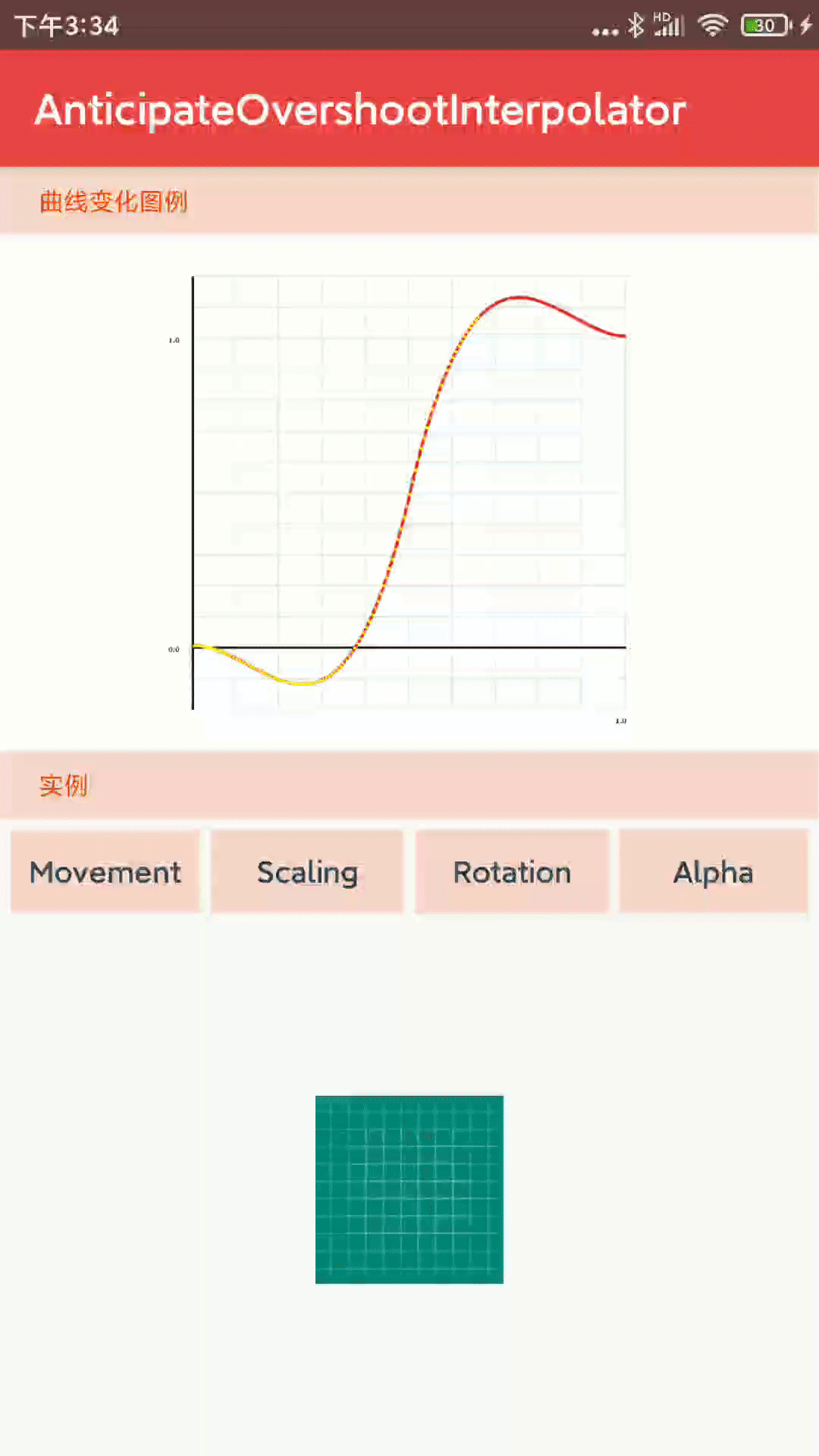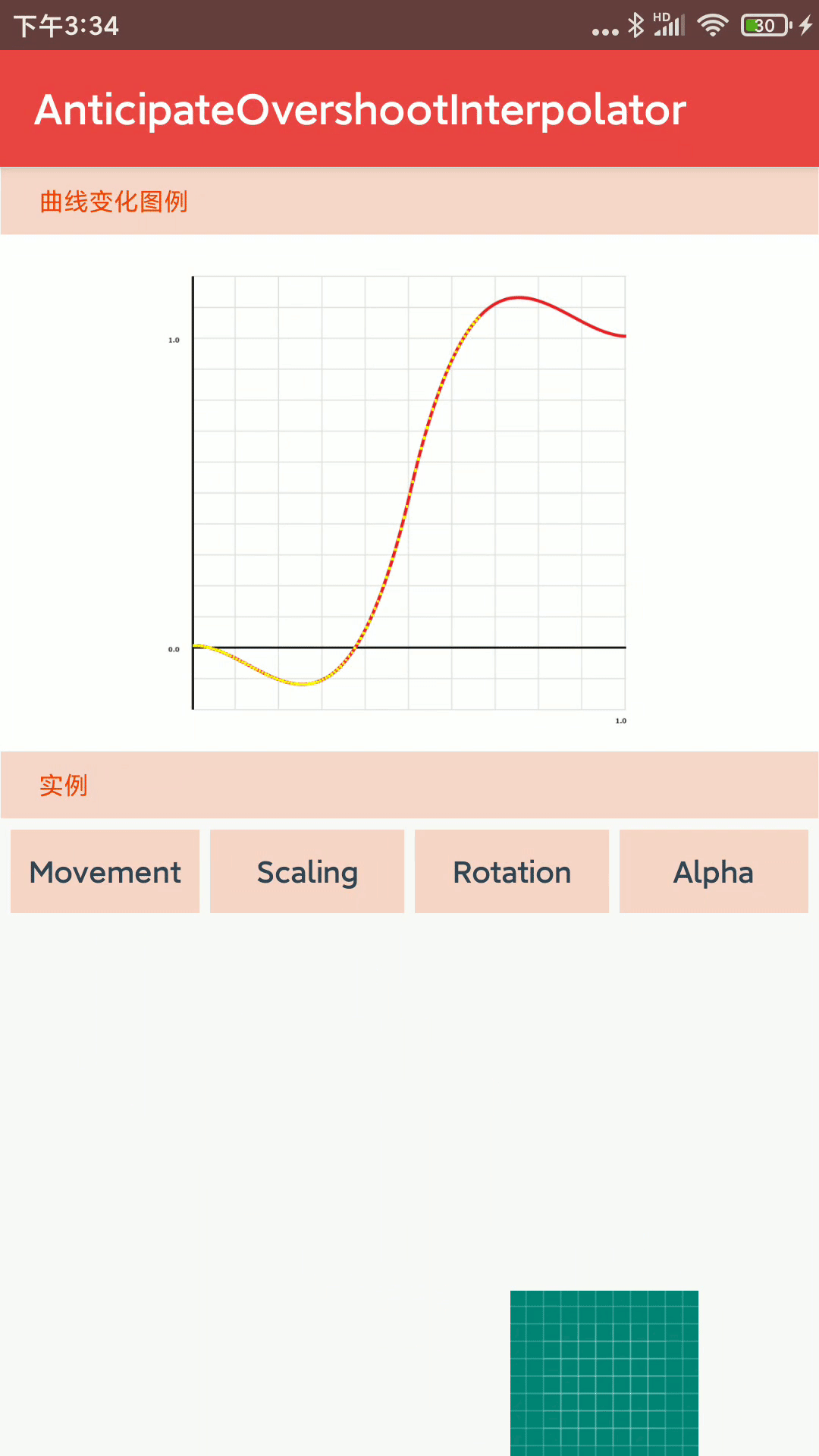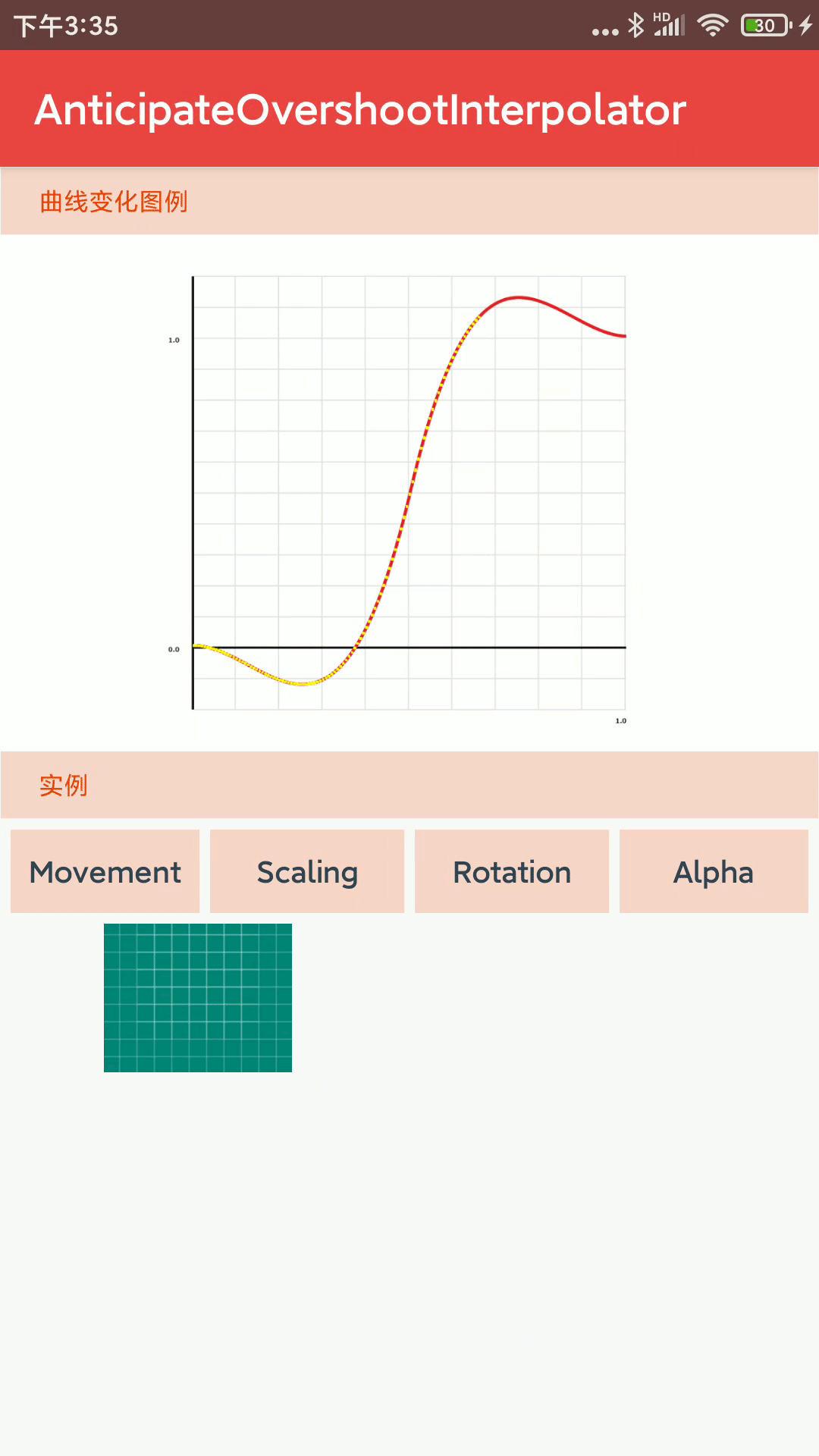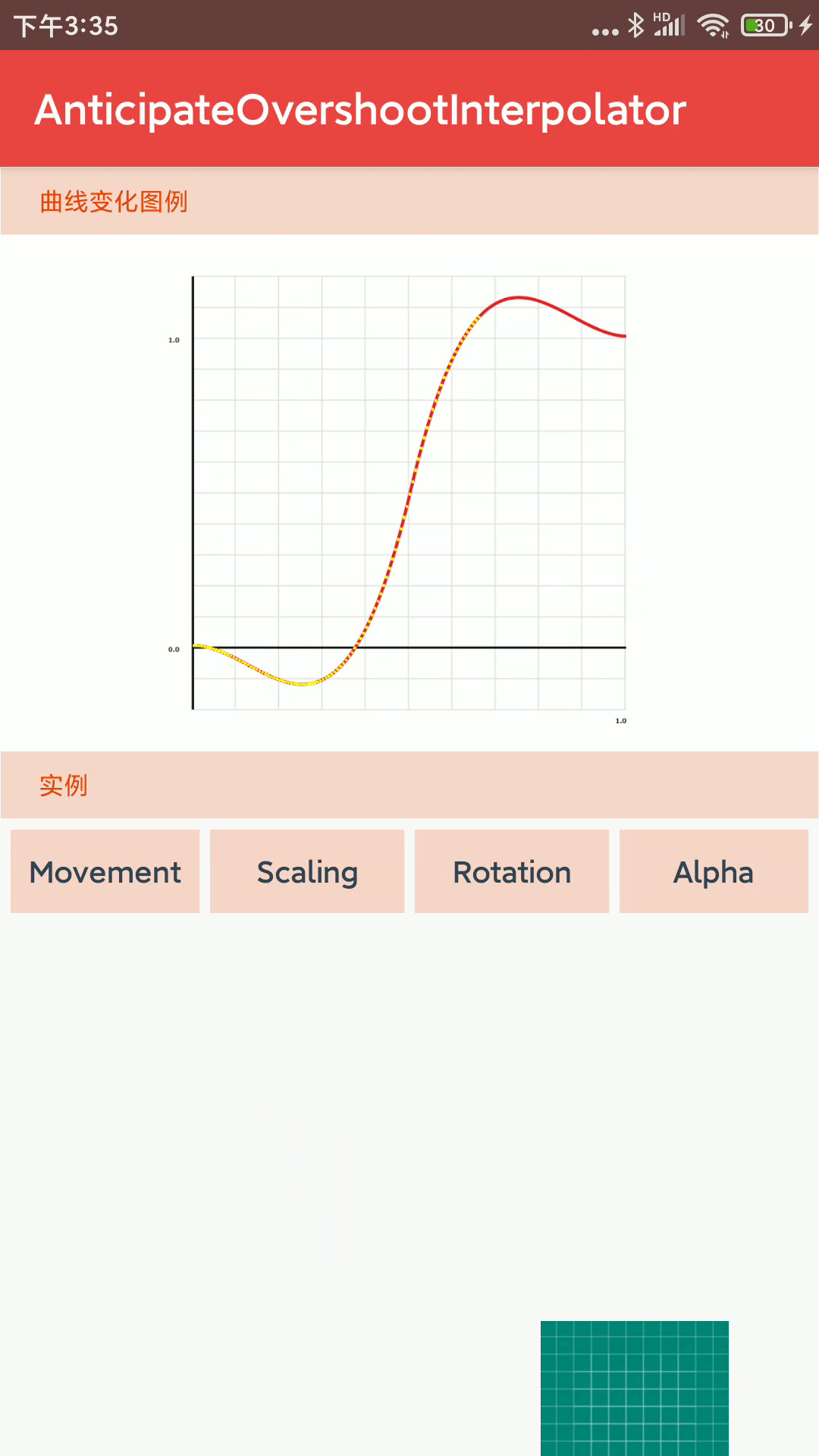
- 核心代码:
public class AnticipateOvershootInterpolator extends BaseInterpolator
implements NativeInterpolator {
private final float mTension;
...//省略部分方法
public AnticipateOvershootInterpolator() {
mTension = 2.0f * 1.5f;
}
/**
* @param tension Amount of anticipation/overshoot. When tension equals 0.0f,
* there is no anticipation/overshoot and the interpolator becomes
* a simple acceleration/deceleration interpolator.
*/
public AnticipateOvershootInterpolator(float tension) {
mTension = tension * 1.5f;
}
private static float a(float t, float s) {
return t * t * ((s + 1) * t - s);
}
private static float o(float t, float s) {
return t * t * ((s + 1) * t + s);
}
public float getInterpolation(float t) {
// a(t, s) = t * t * ((s + 1) * t - s)
// o(t, s) = t * t * ((s + 1) * t + s)
// f(t) = 0.5 * a(t * 2, tension * extraTension), when t < 0.5
// f(t) = 0.5 * (o(t * 2 - 2, tension * extraTension) + 2), when t <= 1.0
if (t < 0.5f) return 0.5f * a(t * 2.0f, mTension);
else return 0.5f * (o(t * 2.0f - 2.0f, mTension) + 2.0f);
}
}
1-1-6、 BounceInterpolator 到达临界值之后会做衰减回弹效果,类似于高空掉落的皮球效果
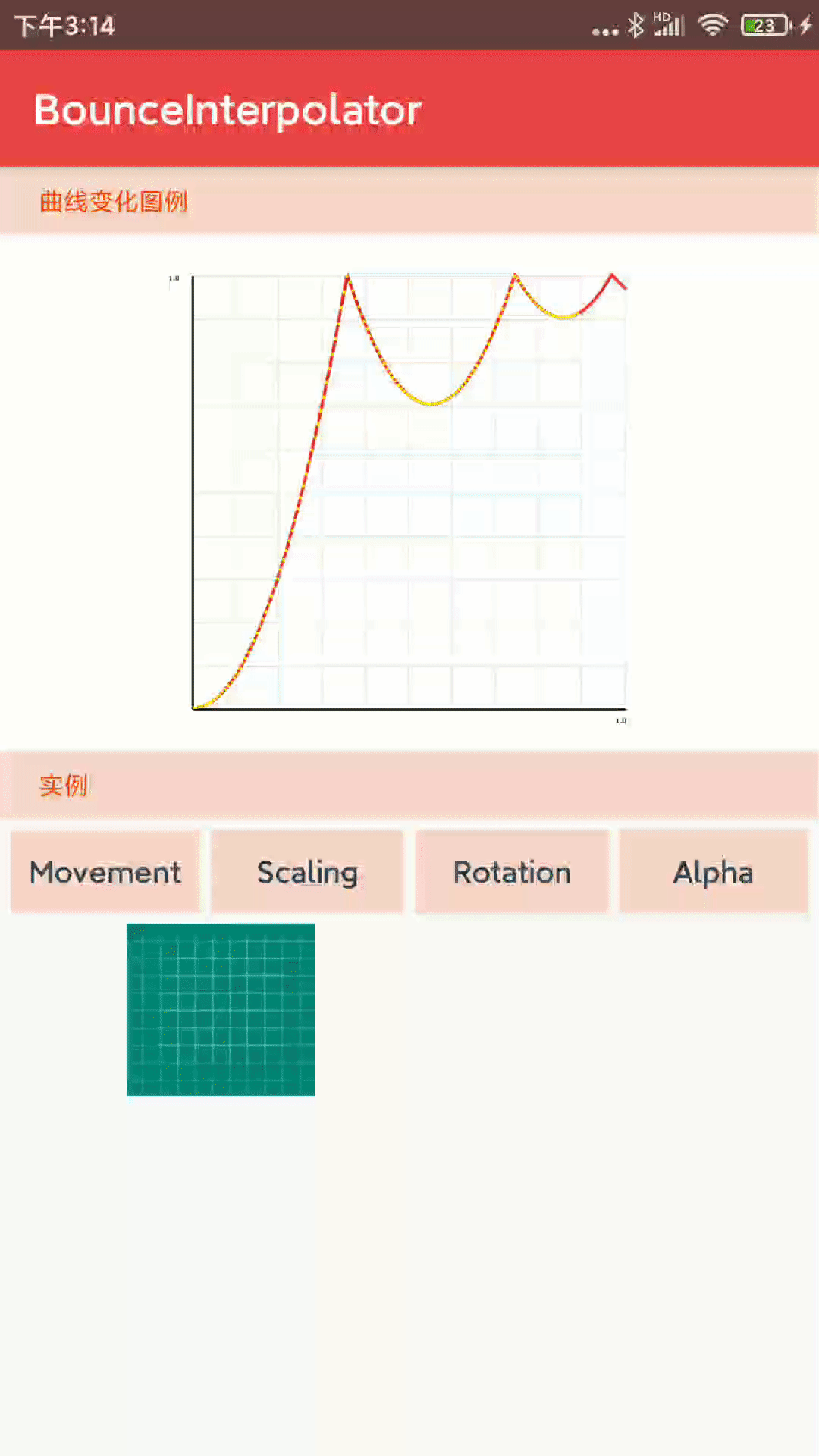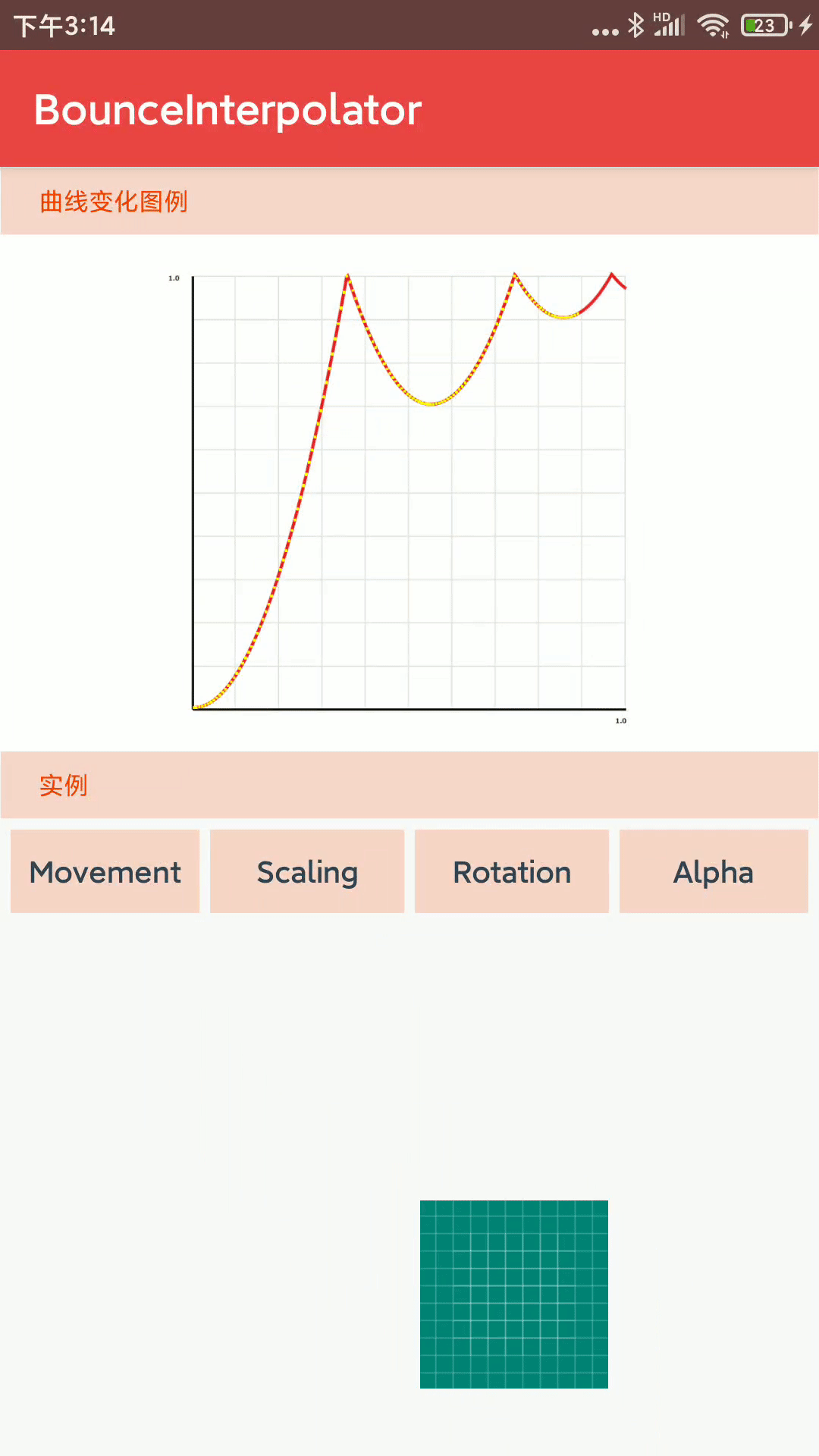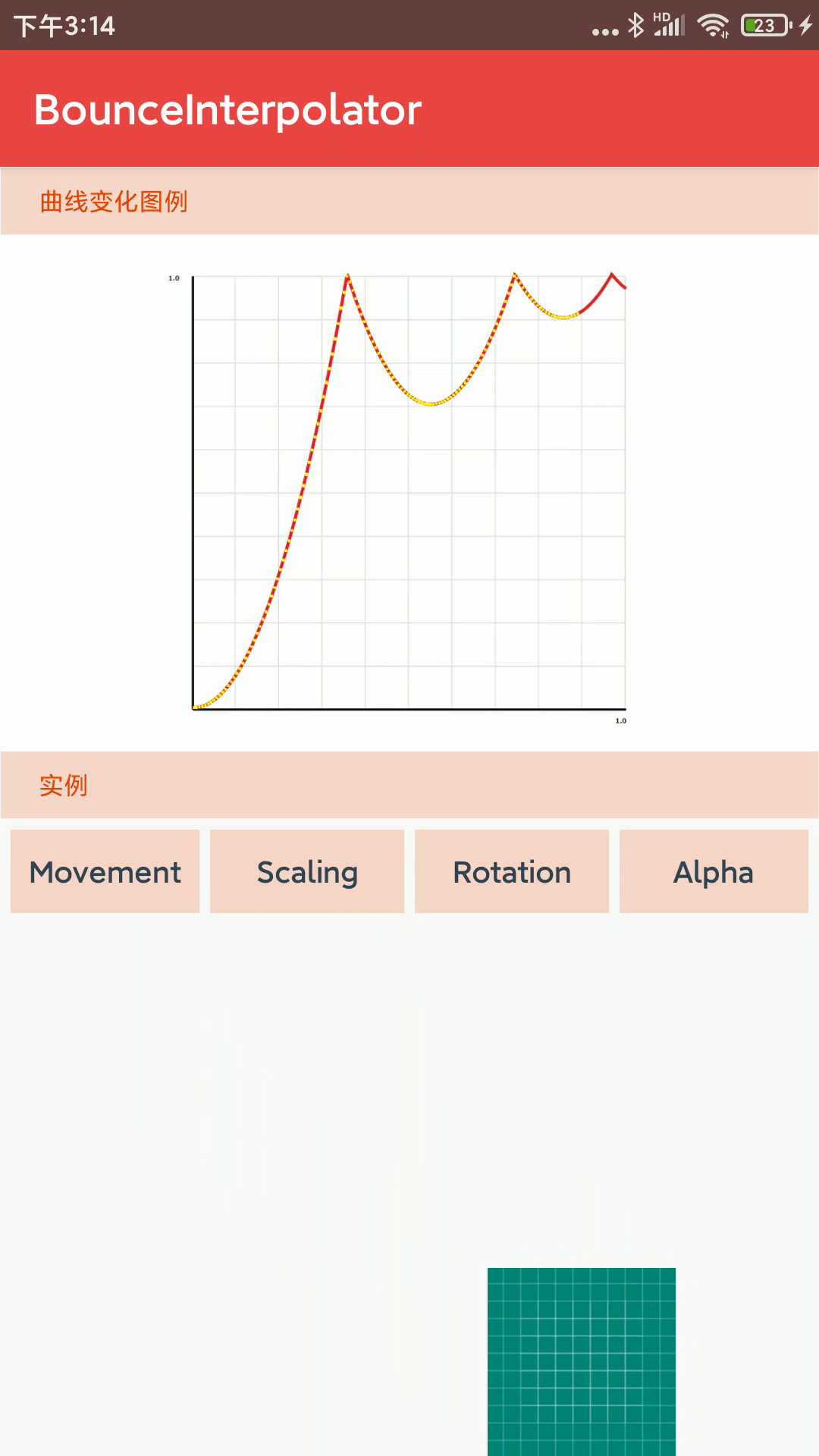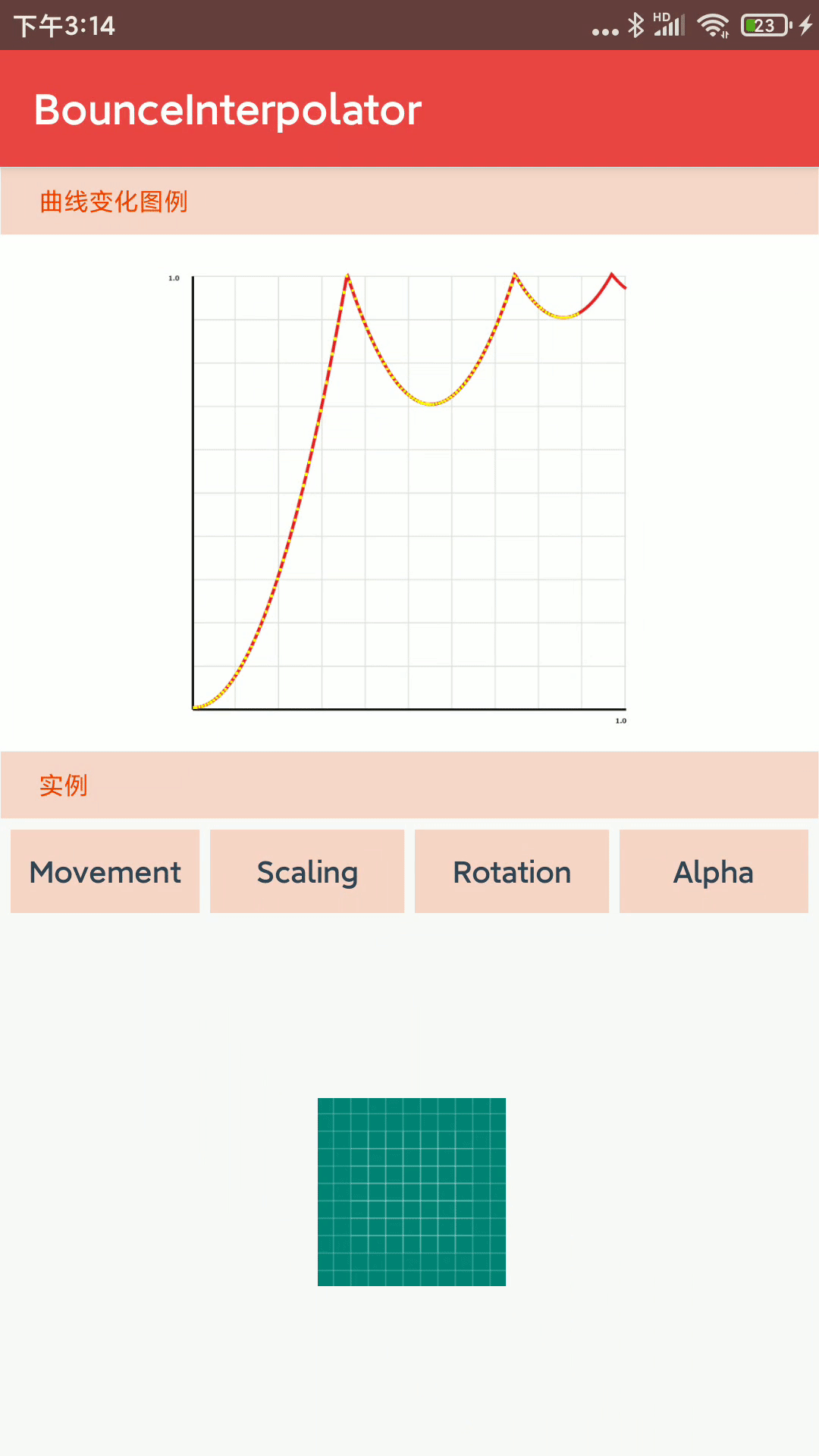
- 核心代码:
public class BounceInterpolator extends BaseInterpolator implements NativeInterpolator {
public BounceInterpolator() {
}
...//省略部分方法
@SuppressWarnings({"UnusedDeclaration"})
public BounceInterpolator(Context context, AttributeSet attrs) {
}
private static float bounce(float t) {
return t * t * 8.0f;
}
public float getInterpolation(float t) {
// _b(t) = t * t * 8
// bs(t) = _b(t) for t < 0.3535
// bs(t) = _b(t - 0.54719) + 0.7 for t < 0.7408
// bs(t) = _b(t - 0.8526) + 0.9 for t < 0.9644
// bs(t) = _b(t - 1.0435) + 0.95 for t <= 1.0
// b(t) = bs(t * 1.1226)
t *= 1.1226f;
if (t < 0.3535f) return bounce(t);
else if (t < 0.7408f) return bounce(t - 0.54719f) + 0.7f;
else if (t < 0.9644f) return bounce(t - 0.8526f) + 0.9f;
else return bounce(t - 1.0435f) + 0.95f;
}
}
1-1-7、 CycleInterpolator沿着正弦函数轨迹运动
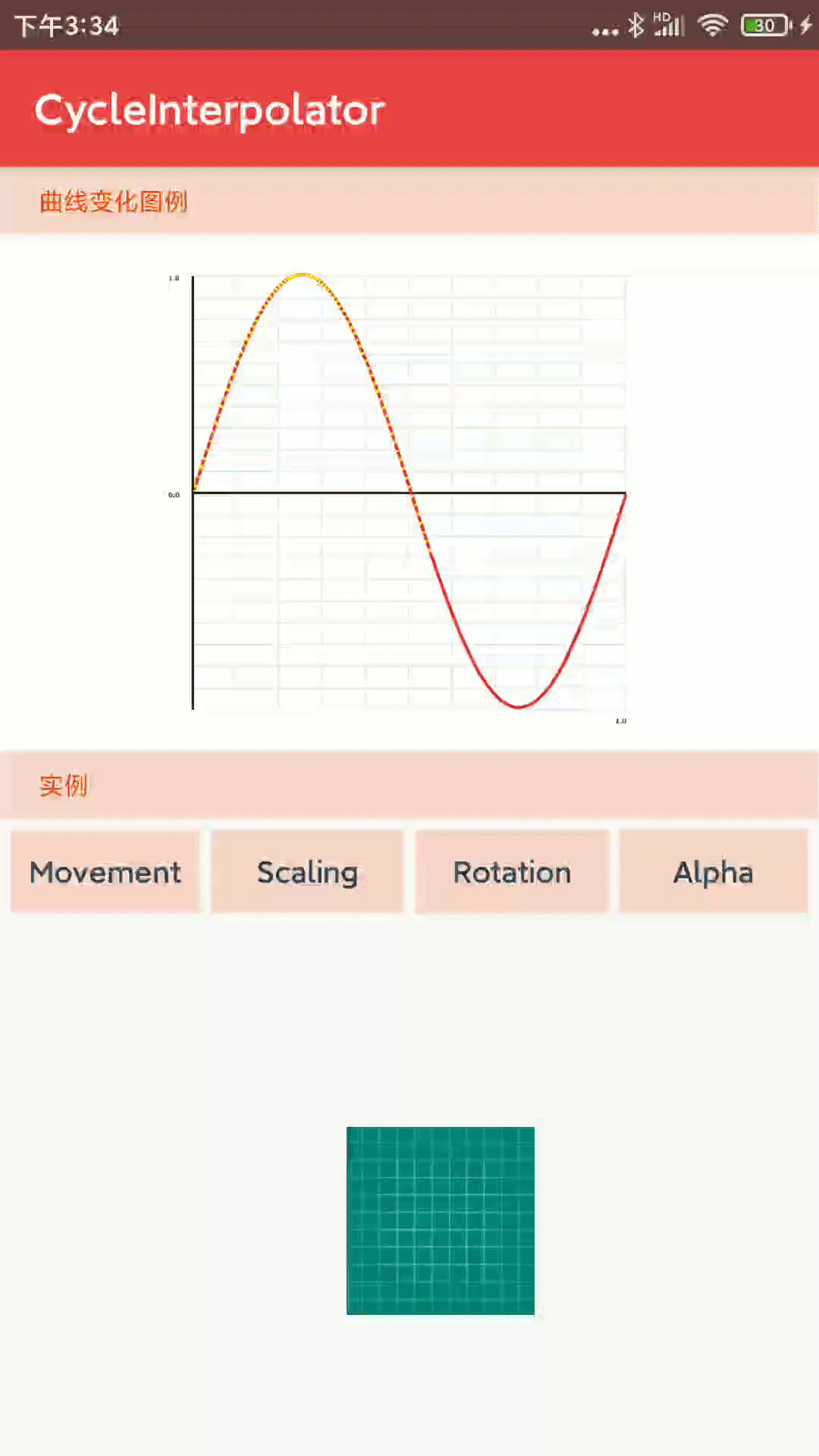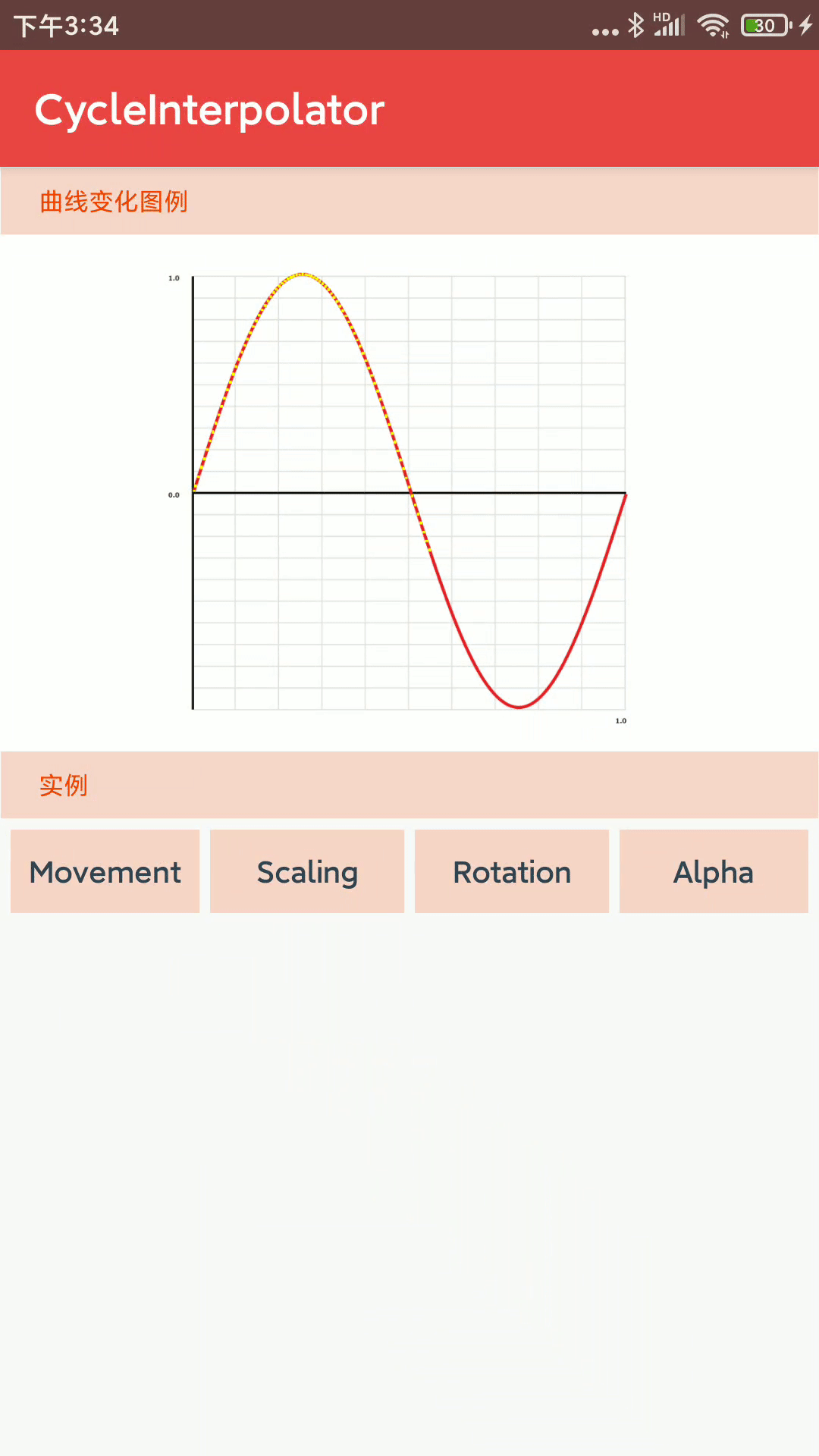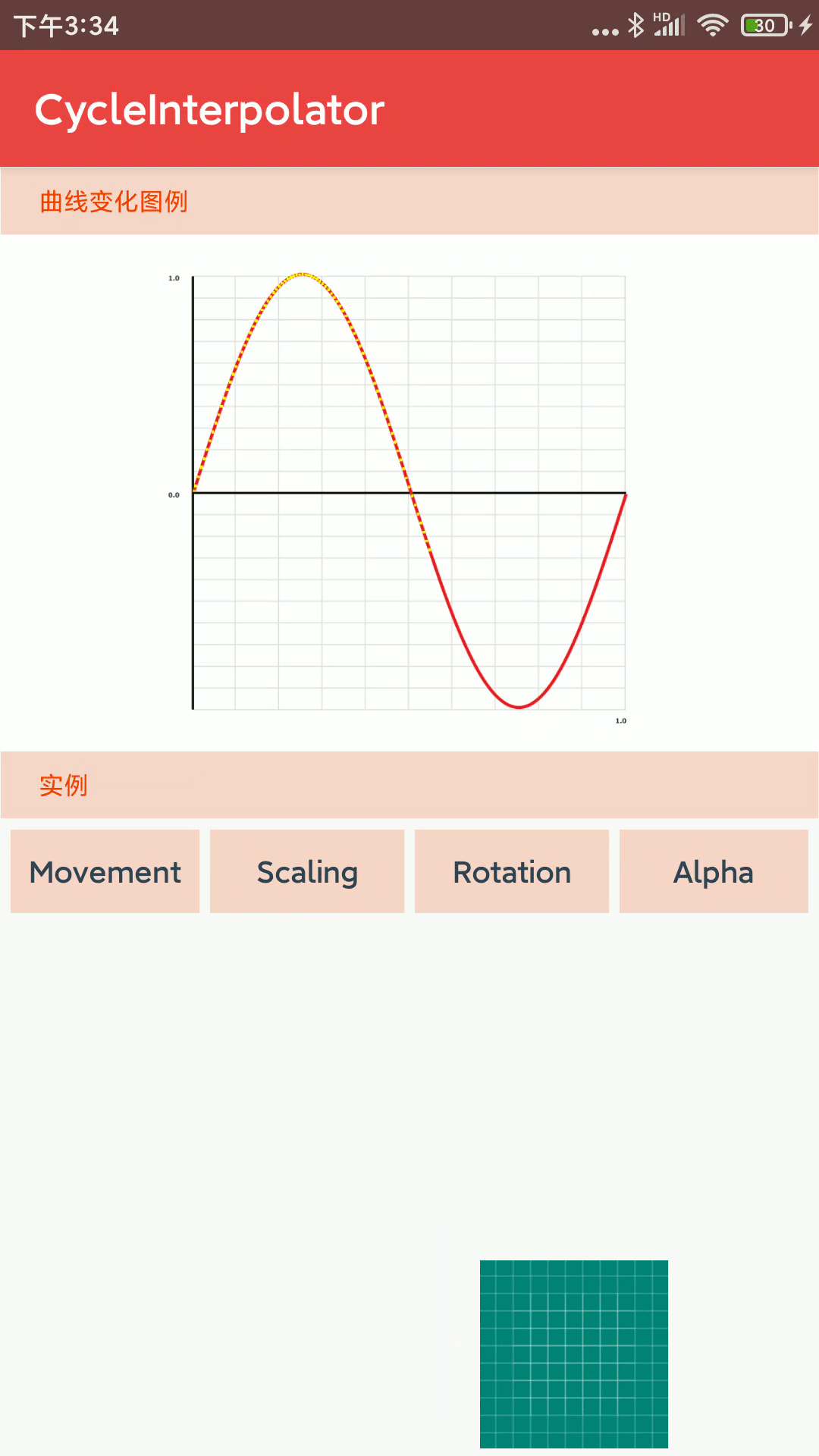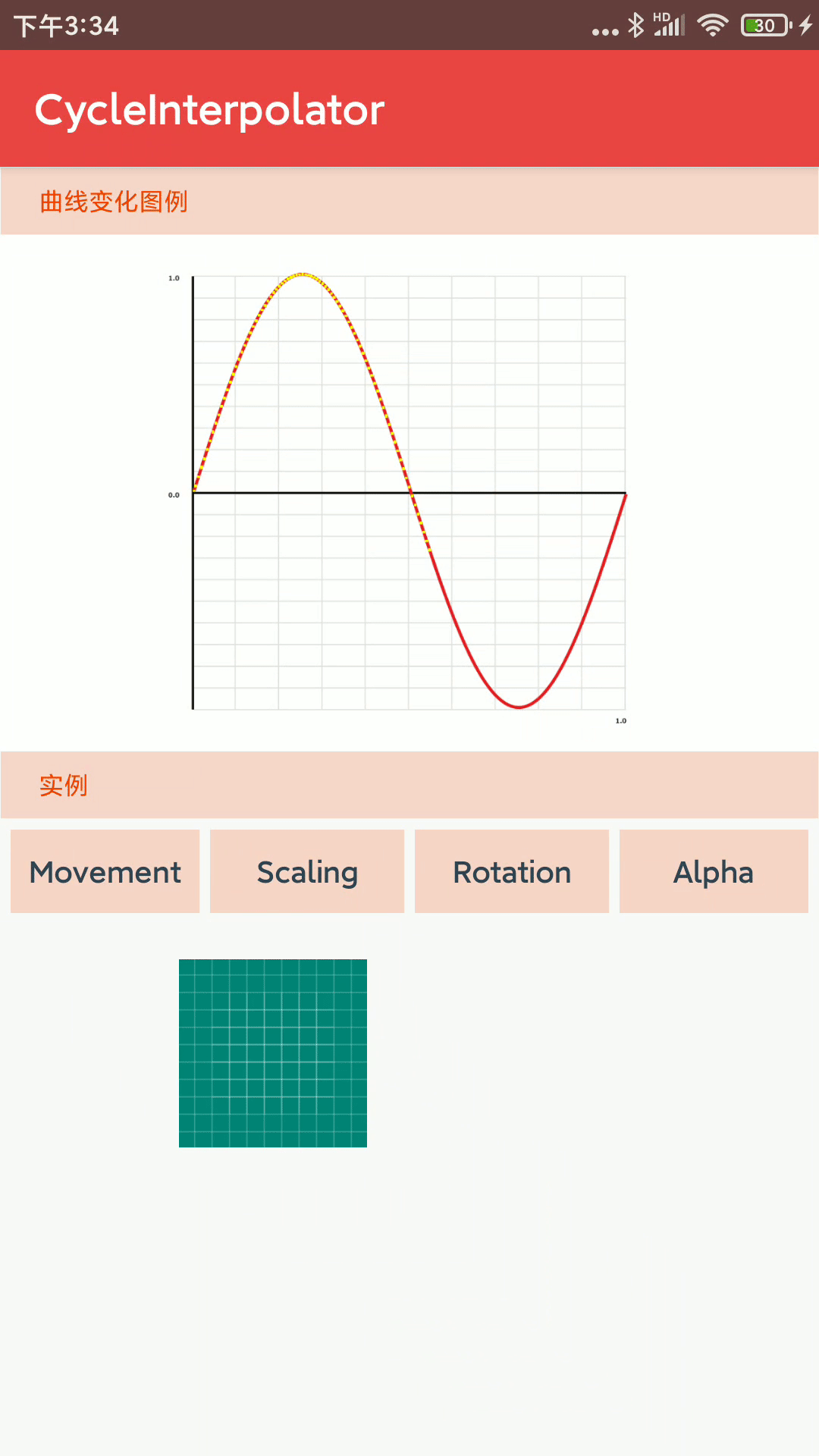
- 核心代码:
public class CycleInterpolator extends BaseInterpolator implements NativeInterpolator {
public CycleInterpolator(float cycles) {
mCycles = cycles;
}
...//省略部分方法
public float getInterpolation(float input) {
return (float)(Math.sin(2 * mCycles * Math.PI * input));
}
private float mCycles;
}
1-1-8、 OvershootInterpolator 加速运动一段,再减速,并超过临界点在运动一会距离。
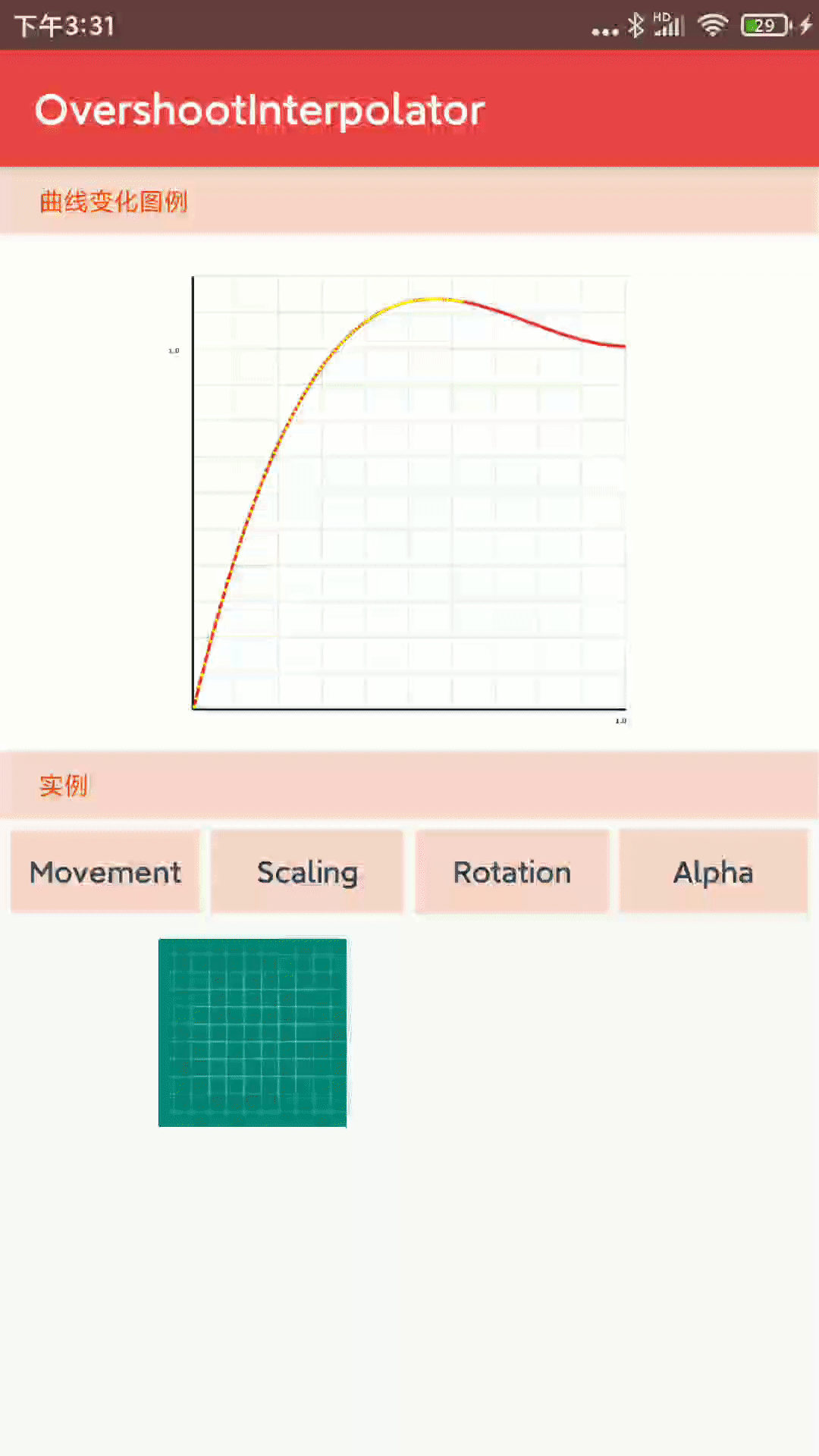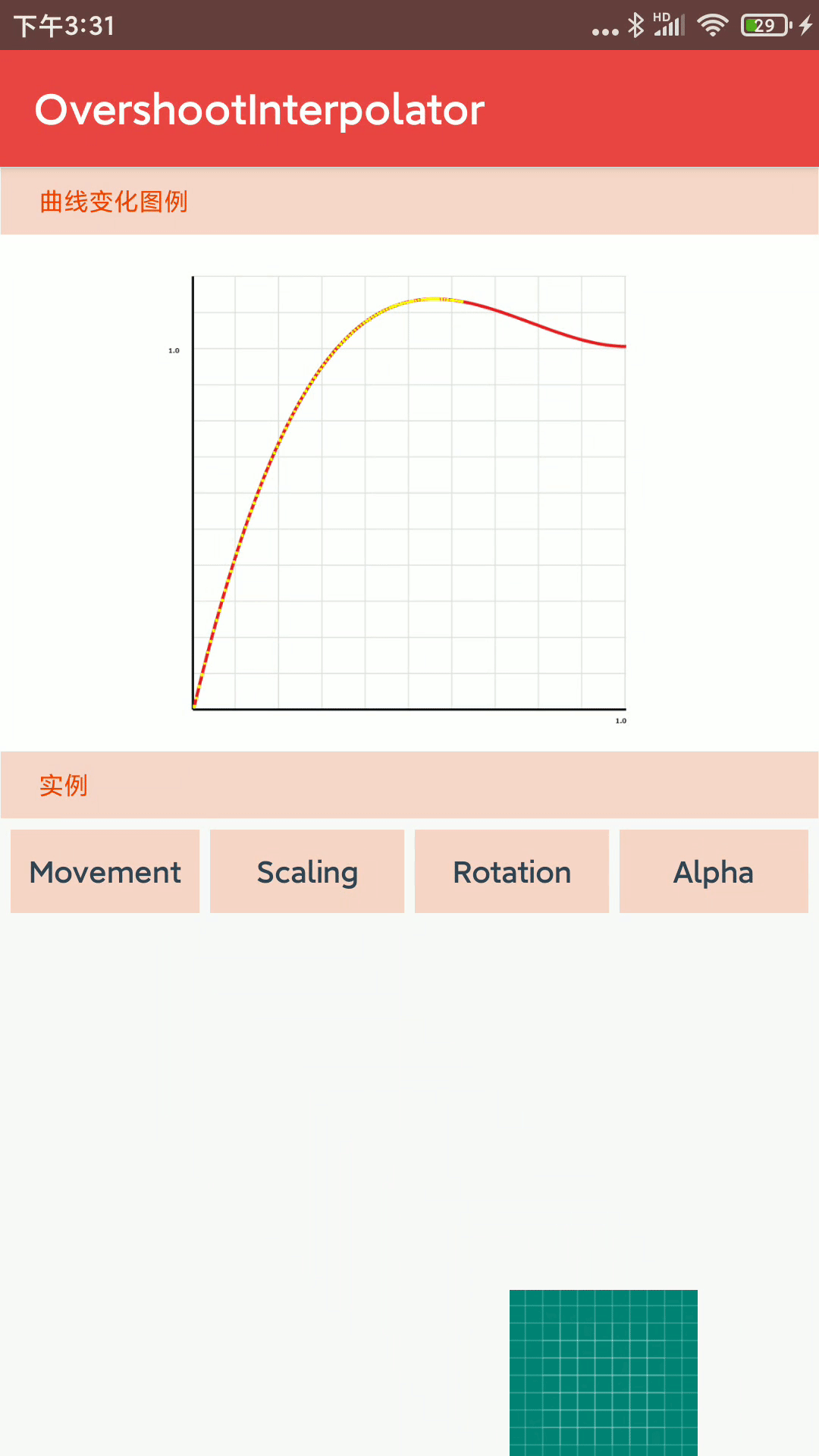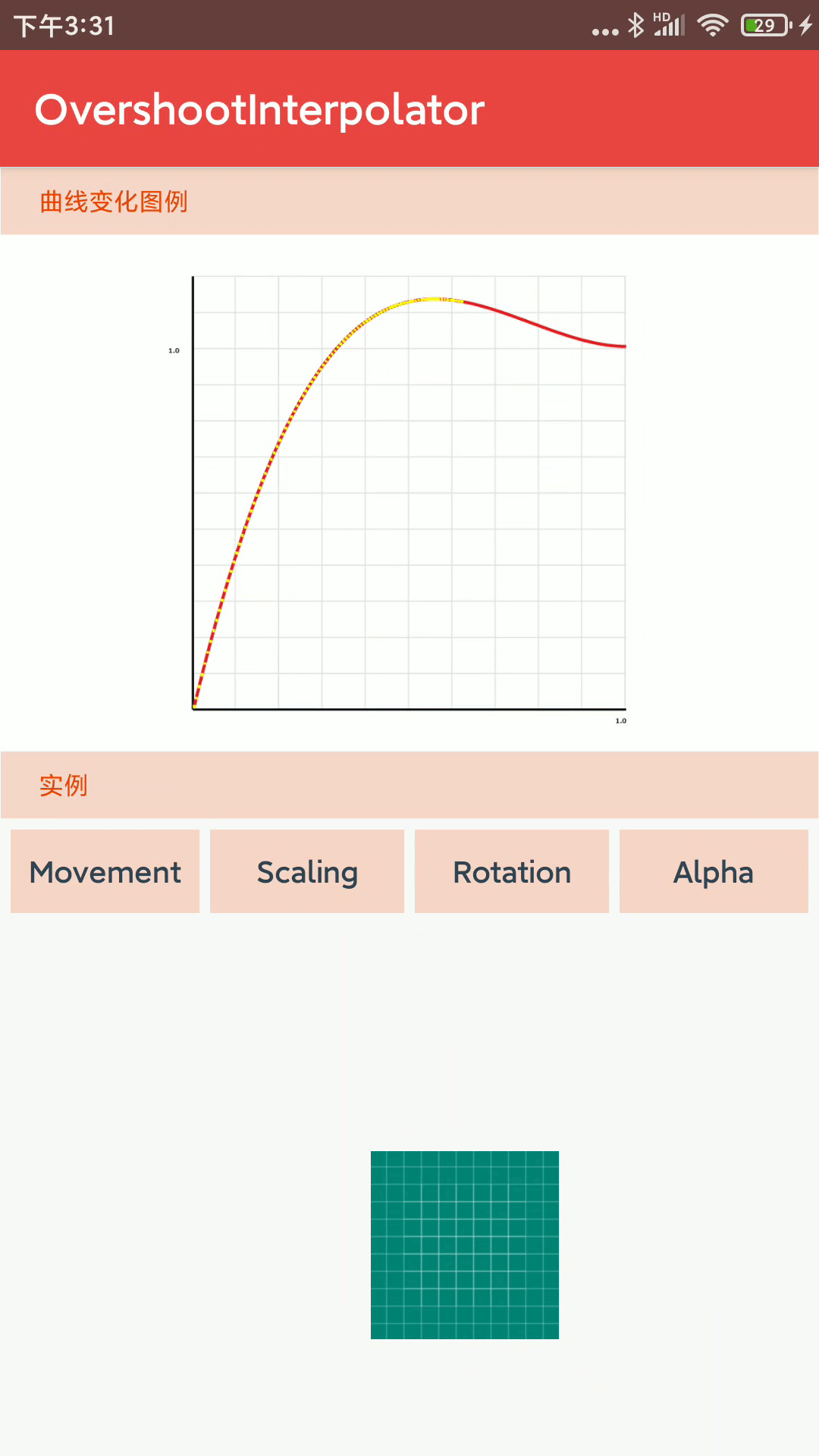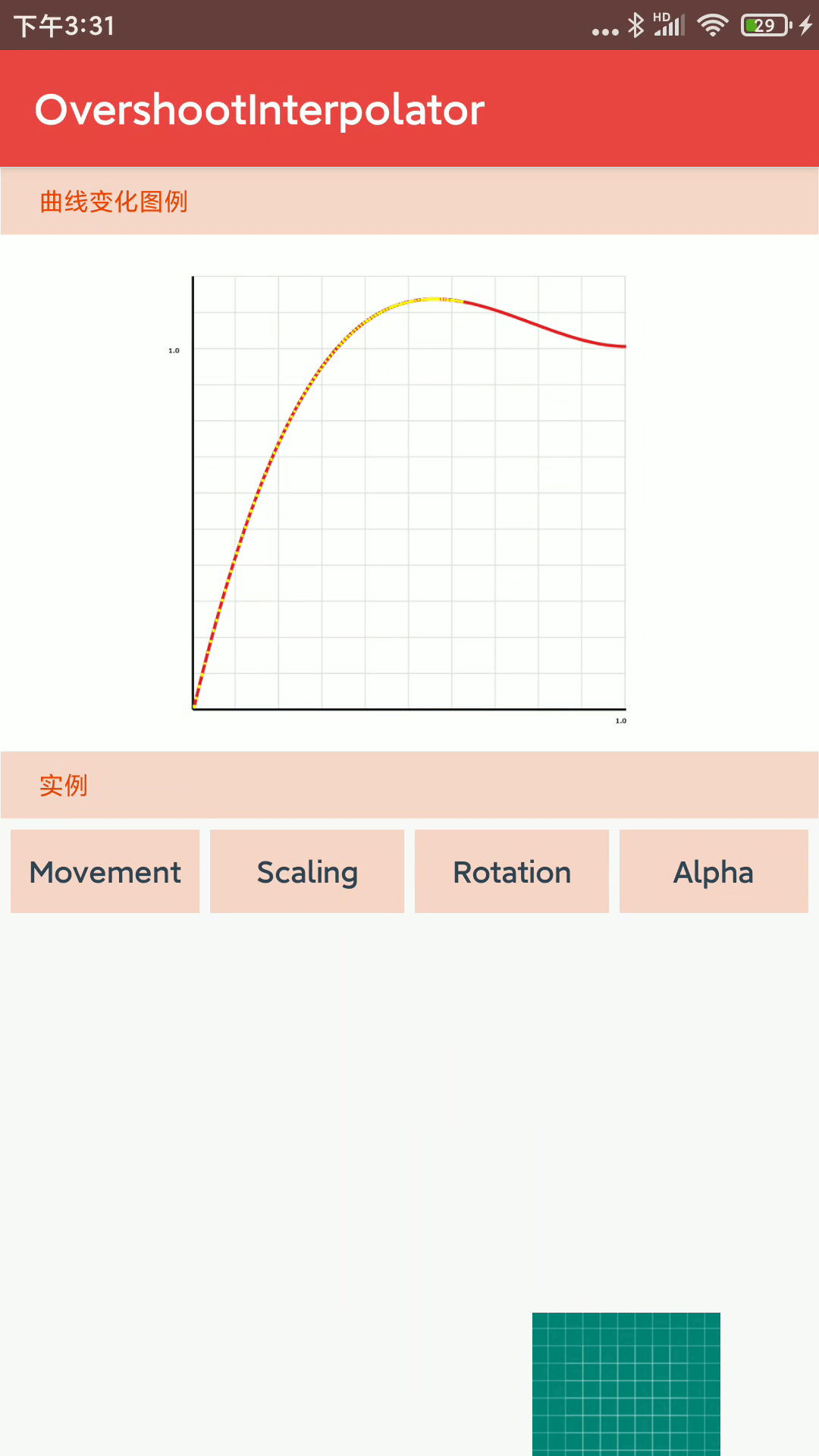
- 核心代码:
public class OvershootInterpolator extends BaseInterpolator implements NativeInterpolator {
private final float mTension;
public OvershootInterpolator() {
mTension = 2.0f;
}
...//省略部分方法
/**
* @param tension Amount of overshoot. When tension equals 0.0f, there is
* no overshoot and the interpolator becomes a simple
* deceleration interpolator.
*/
public OvershootInterpolator(float tension) {
mTension = tension;
}
public float getInterpolation(float t) {
// _o(t) = t * t * ((tension + 1) * t + tension)
// o(t) = _o(t - 1) + 1
t -= 1.0f;
return t * t * ((mTension + 1) * t + mTension) + 1.0f;
}
}
1-1-9、 PathInterpolator 万能插值器,你可以直接传入一个path,根据path路径运行
- 核心代码:
public class PathInterpolator extends BaseInterpolator implements NativeInterpolator {
...//省略部分方法
// This governs how accurate the approximation of the Path is.
private static final float PRECISION = 0.002f;
private float[] mX; // x coordinates in the line
private float[] mY; // y coordinates in the line
/**
* Create an interpolator for an arbitrary <code>Path</code>. The <code>Path</code>
* must begin at <code>(0, 0)</code> and end at <code>(1, 1)</code>.
*
* @param path The <code>Path</code> to use to make the line representing the interpolator.
*/
public PathInterpolator(Path path) {
initPath(path);
}
/**
* Create an interpolator for a quadratic Bezier curve. The end points
* <code>(0, 0)</code> and <code>(1, 1)</code> are assumed.
*
* @param controlX The x coordinate of the quadratic Bezier control point.
* @param controlY The y coordinate of the quadratic Bezier control point.
*/
public PathInterpolator(float controlX, float controlY) {
initQuad(controlX, controlY);
}
/**
* Create an interpolator for a cubic Bezier curve. The end points
* <code>(0, 0)</code> and <code>(1, 1)</code> are assumed.
*
* @param controlX1 The x coordinate of the first control point of the cubic Bezier.
* @param controlY1 The y coordinate of the first control point of the cubic Bezier.
* @param controlX2 The x coordinate of the second control point of the cubic Bezier.
* @param controlY2 The y coordinate of the second control point of the cubic Bezier.
*/
public PathInterpolator(float controlX1, float controlY1, float controlX2, float controlY2) {
initCubic(controlX1, controlY1, controlX2, controlY2);
}
public PathInterpolator(Context context, AttributeSet attrs) {
this(context.getResources(), context.getTheme(), attrs);
}
/** @hide */
public PathInterpolator(Resources res, Theme theme, AttributeSet attrs) {
TypedArray a;
if (theme != null) {
a = theme.obtainStyledAttributes(attrs, R.styleable.PathInterpolator, 0, 0);
} else {
a = res.obtainAttributes(attrs, R.styleable.PathInterpolator);
}
parseInterpolatorFromTypeArray(a);
setChangingConfiguration(a.getChangingConfigurations());
a.recycle();
}
private void parseInterpolatorFromTypeArray(TypedArray a) {
// If there is pathData defined in the xml file, then the controls points
// will be all coming from pathData.
if (a.hasValue(R.styleable.PathInterpolator_pathData)) {
String pathData = a.getString(R.styleable.PathInterpolator_pathData);
Path path = PathParser.createPathFromPathData(pathData);
if (path == null) {
throw new InflateException("The path is null, which is created"
+ " from " + pathData);
}
initPath(path);
} else {
if (!a.hasValue(R.styleable.PathInterpolator_controlX1)) {
throw new InflateException("pathInterpolator requires the controlX1 attribute");
} else if (!a.hasValue(R.styleable.PathInterpolator_controlY1)) {
throw new InflateException("pathInterpolator requires the controlY1 attribute");
}
float x1 = a.getFloat(R.styleable.PathInterpolator_controlX1, 0);
float y1 = a.getFloat(R.styleable.PathInterpolator_controlY1, 0);
boolean hasX2 = a.hasValue(R.styleable.PathInterpolator_controlX2);
boolean hasY2 = a.hasValue(R.styleable.PathInterpolator_controlY2);
if (hasX2 != hasY2) {
throw new InflateException(
"pathInterpolator requires both controlX2 and controlY2 for cubic Beziers.");
}
if (!hasX2) {
initQuad(x1, y1);
} else {
float x2 = a.getFloat(R.styleable.PathInterpolator_controlX2, 0);
float y2 = a.getFloat(R.styleable.PathInterpolator_controlY2, 0);
initCubic(x1, y1, x2, y2);
}
}
}
private void initQuad(float controlX, float controlY) {
Path path = new Path();
path.moveTo(0, 0);
path.quadTo(controlX, controlY, 1f, 1f);
initPath(path);
}
private void initCubic(float x1, float y1, float x2, float y2) {
Path path = new Path();
path.moveTo(0, 0);
path.cubicTo(x1, y1, x2, y2, 1f, 1f);
initPath(path);
}
private void initPath(Path path) {
float[] pointComponents = path.approximate(PRECISION);
int numPoints = pointComponents.length / 3;
if (pointComponents[1] != 0 || pointComponents[2] != 0
|| pointComponents[pointComponents.length - 2] != 1
|| pointComponents[pointComponents.length - 1] != 1) {
throw new IllegalArgumentException("The Path must start at (0,0) and end at (1,1)");
}
mX = new float[numPoints];
mY = new float[numPoints];
float prevX = 0;
float prevFraction = 0;
int componentIndex = 0;
for (int i = 0; i < numPoints; i++) {
float fraction = pointComponents[componentIndex++];
float x = pointComponents[componentIndex++];
float y = pointComponents[componentIndex++];
if (fraction == prevFraction && x != prevX) {
throw new IllegalArgumentException(
"The Path cannot have discontinuity in the X axis.");
}
if (x < prevX) {
throw new IllegalArgumentException("The Path cannot loop back on itself.");
}
mX[i] = x;
mY[i] = y;
prevX = x;
prevFraction = fraction;
}
}
/**
* Using the line in the Path in this interpolator that can be described as
* <code>y = f(x)</code>, finds the y coordinate of the line given <code>t</code>
* as the x coordinate. Values less than 0 will always return 0 and values greater
* than 1 will always return 1.
*
* @param t Treated as the x coordinate along the line.
* @return The y coordinate of the Path along the line where x = <code>t</code>.
* @see Interpolator#getInterpolation(float)
*/
@Override
public float getInterpolation(float t) {
if (t <= 0) {
return 0;
} else if (t >= 1) {
return 1;
}
// Do a binary search for the correct x to interpolate between.
int startIndex = 0;
int endIndex = mX.length - 1;
while (endIndex - startIndex > 1) {
int midIndex = (startIndex + endIndex) / 2;
if (t < mX[midIndex]) {
endIndex = midIndex;
} else {
startIndex = midIndex;
}
}
float xRange = mX[endIndex] - mX[startIndex];
if (xRange == 0) {
return mY[startIndex];
}
float tInRange = t - mX[startIndex];
float fraction = tInRange / xRange;
float startY = mY[startIndex];
float endY = mY[endIndex];
return startY + (fraction * (endY - startY));
}
}
插值器的使用很简单。
java文件中使用
android:interpolator="@android:anim/accelerate_decelerate_interpolator"
xml文件中使用
scaleAnimation.interpolator = LinearInterpolator()
1-2、自定义插值器
接下来我们实现一个如下的曲线

下面是实现代码,从上面系统的实现,基本上可以知道,核心就是要实现Interpolator接口。在getInterpolation(input: Float): Float 中书写计算算法。
其实上面的图上,算法已经列出来了,只需要写到这个方法即可。
class EaseInElasticInterpolator: Interpolator {
override fun getInterpolation(input: Float): Float {
val c4 = (2 * Math.PI) / 3
return when (input) {
0F -> {
0F
}
1F -> {
1F
}
else -> {
((-2.0).pow((10 * input - 10).toDouble()) * sin((input * 10F - 10.75F) * c4)).toFloat()
}
}
}
}
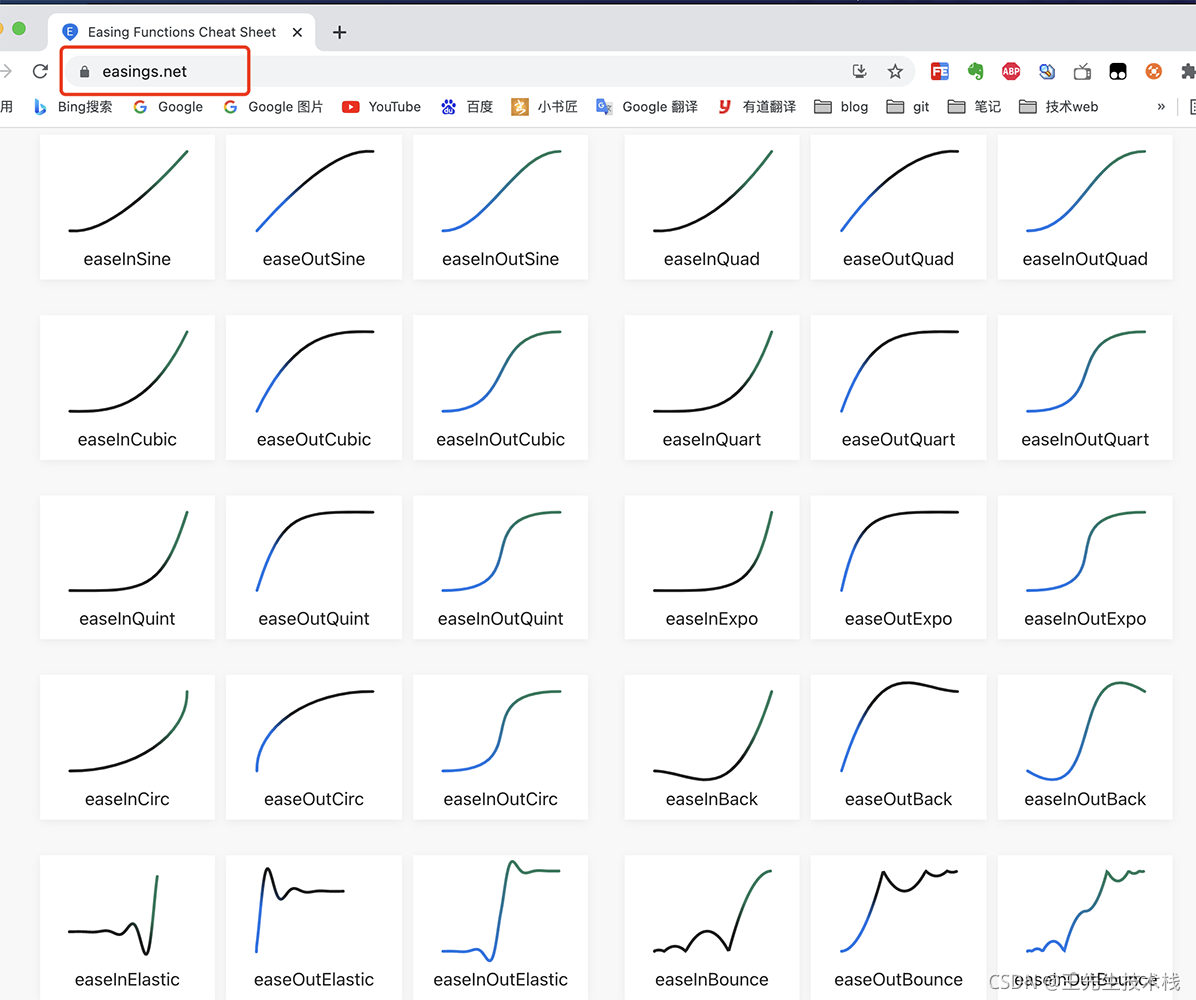
介绍几个很好用的辅助网站,可以帮我们实现事半功倍的效果。
-
easings 是一个开源的插值器算法网站,涵盖了各种各样的插值器算法,绝大部分的物理场景都能找到。
https://github.com/ai/easings.net





























 1926
1926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








