1885：【14NOIP提高组】寻找道路

【题目描述】

在有向图G中，每条边的长度均为1，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2．在满足条件1的情况下使路径最短。

注意：图G中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

【输入】

第一行有两个用一个空格隔开的整数n和m，表示图有n个点和m条边。

接下来的m行每行2个整数x、y，之间用一个空格隔开，表示有一条边从点x指向点y。

最后一行有两个用一个空格隔开的整数s、t，表示起点为s，终点为t。

【输出】

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出-1。

【输入样例】

3 2
1 2
2 1
1 3

【输出样例】

-1

【提示】

【输入输出样例说明】

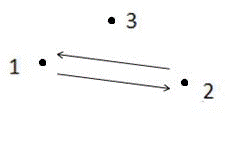
如上图所示，箭头表示有向道路，圆点表示城市。起点1与终点3不连通，所以满足题目描述的路径不存在，故输出-1。

【输入输出样例2】

输入：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出:

3

【输入输出样例说明】

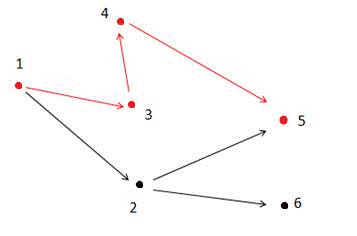
如上图所示，满足条件的路径为1->3->4->5。注意点2不能在答案路径中，因为点2连了一条边到点6，而点6不与终点 5 连通。

【数据说明】

对于30%的数据，0<n≤10，0<m≤ 20；

对于60%的数据，0 <n≤100，0<m≤2000；

对于100%的数据，0 <n≤10,000，0<m≤200,000，0< x，y，s，t≤n，x≠t。

直接手搓AC代码：

#include <iostream>
#include <vector>
#include <queue>
#define maxn 10005
using namespace std;
int n, m, s, t;
vector<int> g[maxn], gt[maxn];
bool visited[maxn];
int dist[maxn];
int mark[maxn]; // 0/1表示该点与终点不连通/联通，-1表示该点指向标记0的点
void dfs(int k)
{
    mark[k] = 1;
    for (int i = 0; i < gt[k].size(); i++)
    {
        if (!visited[gt[k][i]])
        {
            visited[gt[k][i]] = true;
            dfs(gt[k][i]);
        }
    }
}
void bfs()
{
    queue<int> q;
    q.push(s);
    while (!q.empty() && dist[t] == 0)
    {
        int k = q.front();
        q.pop();
        if (mark[k] == 1)
        {
            for (int i = 0; i < g[k].size(); i++)
            {
                if (!dist[g[k][i]])
                {
                    dist[g[k][i]] = dist[k] + 1;
                    q.push(g[k][i]);
                }
            }
        }
    }
}
int main()
{
    cin >> n >> m;
    int a, b;
    for (int i = 1; i <= m; i++)
    {
        cin >> a >> b;
        if (a != b)
        {
            g[a].push_back(b);
            gt[b].push_back(a);
        }
    }
    cin >> s >> t;
    dfs(t);
    for (int i = 1; i <= n; i++)
    {
        if (mark[i] == 0)
        {
            for (int j = 0; j < gt[i].size(); j++)
            {
                mark[gt[i][j]] = -1;
            }
        }
    }
    bfs();
    cout << (dist[t] > 0 ? dist[t] : -1) << endl;
    return 0;