即插即用的OCC结果增强模型 TT-Occ

博客就应该是最自由传播的，不需要关注，不需要会员……

TT-Occ

TT-Occ: Test-Time Compute for Self-Supervised Occupancy via Spatio-Temporal Gaussian Splatting

https://github.com/Xian-Bei/TT-Occ

Abstract

自监督3D占据预测任务可以解决对于大量OCC标注数据的需要，但是训练一个OCC稠密预测任务的模型仍然需要大量的时间和资源，并且训练好的模型对于新增类别和voxel的调整都非常困难，因此本文提出了一种灵活的，可在测试环节即插即用的预测框架TT-Occ。通过在原始数据阶段聚合VLM来优化3DGS的方式：

1. 将3D几何信息与VLM的2D语义特征进行对齐;
2. 在时序上分别对静态和动态目标的GS表征进行聚合训练；
3. 利用优化后的3DGS生成OCC预测结果。

Introduction

本文提出一种又快又省的OCC预测方法，不仅不需要人工标注的真值，甚至不需要一些额外的先验信息(HD地图或OD真值)，进需要原始数据和VLMs,处理思路如图所示：

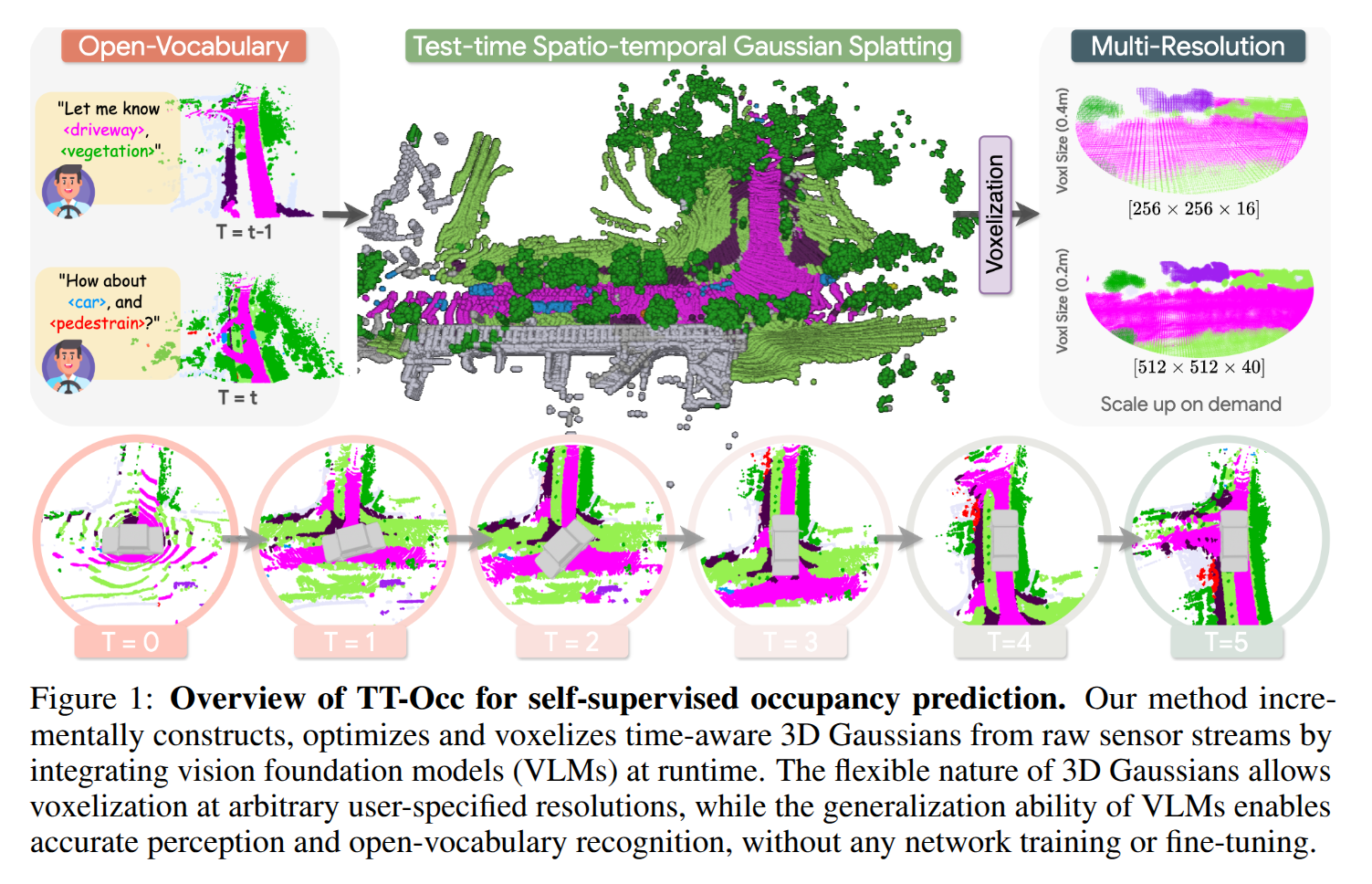
针对不同的输入数据源，给出了两个变体：TT-OccCamera 和 TT-OccLiDAR，而且采用在线推理生成的方法，可以总结为三步走：

1. 在测试阶段，将3D几何信息与VLM的2D语义特征在图像空间上进行对齐，生成的Gaussians可以泼溅到图像上，实现色彩与语义的对齐和优化；
2. 结合时序信息的连续性，分别对动态Gaussians和静态Gaussians进行时序上的跟踪，估计动态Gaussians的运动速度，避免拖影的出现；
3. 在单帧下根据指定的参数对Gaussians进行体素化，同时为了减小VLM预测的不连续和固有噪音的干扰，引入一个三边径向基函数对Gaussians进行平滑。

Related Work

Proposed Approach

Lift Geometry and Semantics into Time-aware Gaussians

每帧的场景都通过与时间相关的Gaussians集合表征，每一个Gaussian通过其平均坐标，不透明度，颜色和语义置信度和时间组成，其空间密度可以表示为：

$$G_i^{(t)}(\mathbf{x})=\exp (-\frac{1}{2}(\mathbf{x}-{\mu }_i{)}^{\top }\sum _i^{-1}(\mathbf{x}-{\mu }_i))$$

其中，协方差矩阵${\sum }_i=R({\mathbf{q}}_i)\text{diag}({\mathbf{s}}_i^2)R({\mathbf{q}}_i{)}^{\top }$通过四元数${\mathbf{q}}_i\in {\mathbb{R}}^4$和缩放因子${\mathbf{s}}_i\in {\mathbb{R}}_{+}^3$进行参数化。在使用相对应的内外参矩阵对Gaussian进行2D泼溅。

对于TT-OccLiDAR，直接使用稀疏的雷达点云作为Gaussian的初始化坐标，而对于TT-OccCamera，则使用VGGT预测深度后对Gaussian进行初始化，通过利用环视图像对一些关键点进行三角化的方式来克服深度估计带来的尺度不一致的问题：

使用前视三张图片、后视三张图的重叠区域进行关键点匹配，过滤掉VGGT预测质量较低的部分后，使用对应相机的内外参对匹配后的点进行三角化，从而得到真实位置与深度预测之间的尺度差异，从而得到与真实世界一致的深度预测结果。

使用OpenSeeD作为VLM得到图像的语义分割结果，使用$\delta$初始化和sigmoid激活函数，避免使用指数函数带来的过度膨胀的问题，并且对同一语义的Gaussians进行修剪合并。

Track Dynamic Gaussians

对于场景中快速移动的物体，在没有一些额外先验(如轨迹或3Dbox)，3DGS的优化很容易带来拖影的问题，如图所示。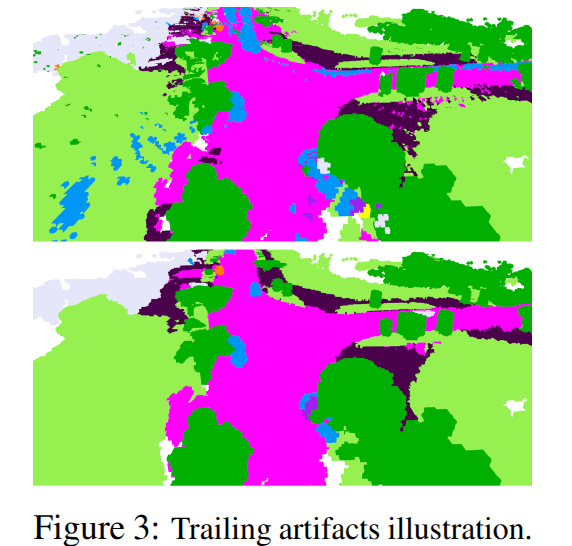

为了解决这一问题，本文拆分动静态Gaussian，对动态Gaussian进行跟踪。

对于静态Gaussian，均直接采用累积的方式，而对于动态Gaussian，TT-OccLiDAR先使用patchwork++进行地面分割，再将2D语义信息与点云进行语义关联，利用DBSCAN进行去噪聚类，再通过KNN和形状相似度进行帧间实例关联，最后使用迭代最近点(ICP)进行3D流场估计。

**TT-OccCamera则使用RAFT估计同一相机相邻帧的光流，并根据VGGT预测的帧间相机姿态和逐像素深度计算自车流场。从而依据自车的运动情况和图像中观测的相对运动得到目标的真实运动状况。但将其直接变换到3D空间会放大噪音的干扰，导致Gaussian运动不稳定。为了缓解这一问题，本文设置了一个最低阈值对流场预测结果进行限制，来得到可能存在移动目标的动态掩码，将这些区域所对应的目标视为是动态目标。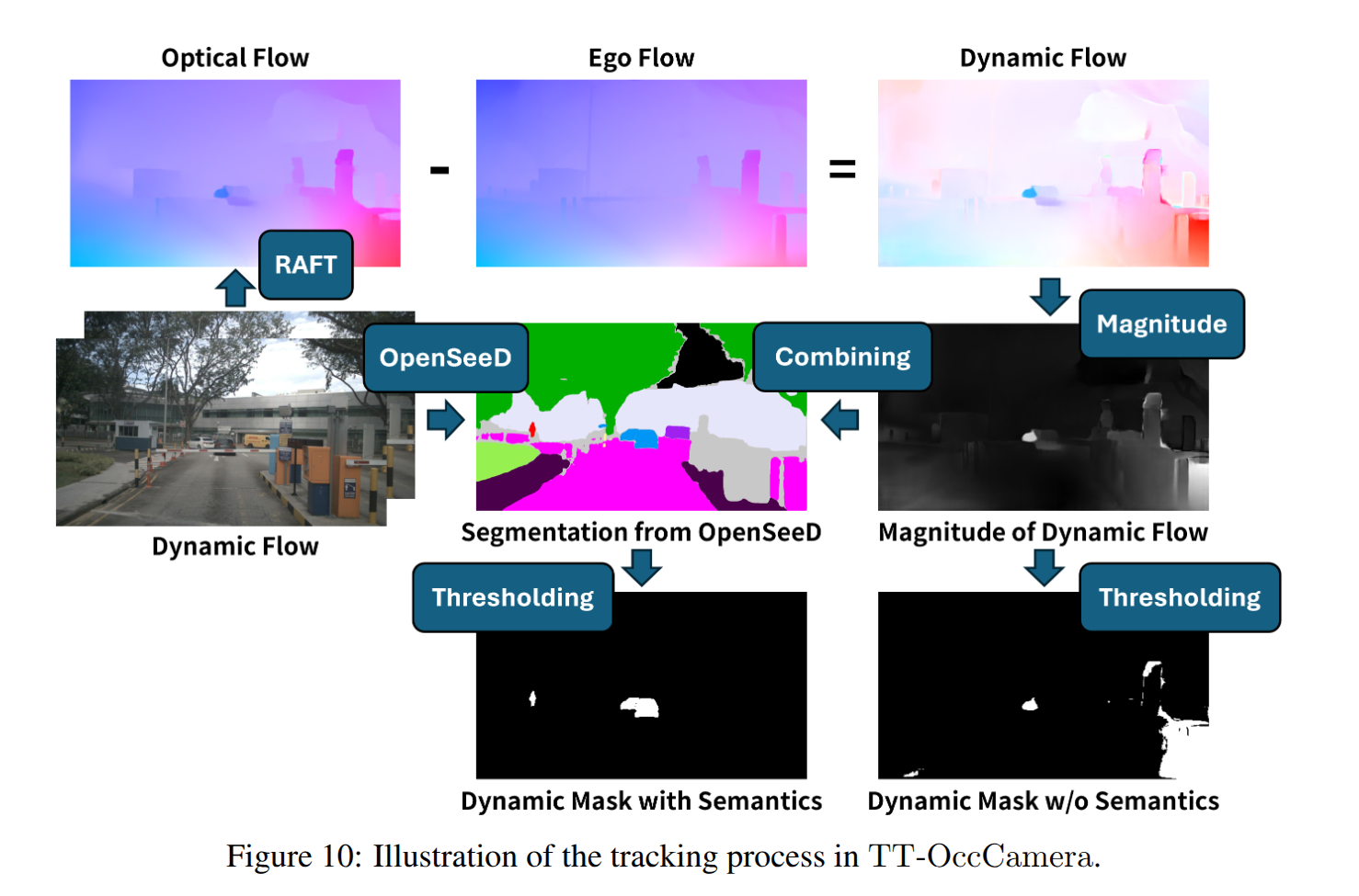
**

Gaussian Voxelization

沿用常规的3DGS方法对Gaussian进行优化更新，同时为了降低VLM结果和动态跟踪的噪音干扰，引入三边径向基函数(TRBF)对连续帧结果进行平滑去噪。TRBF通过利用Gaussians间的空间、辐射范围和语义信息提升占用结果的时空相关性，每个TRBF的核函数可以定义为其最近邻的Dconv：

$${\mathbf{m}}_I\leftarrow \frac{1}{Z(i)}\sum _{j\in NN(i)}{\mathbf{m}}_j\cdot \mathcal{K}(i,j)$$

$$\mathcal{K}(i,j)={\mathcal{K}}_{\mu }(i,j)\cdot {\mathcal{K}}_c(i,j)\cdot {\mathcal{K}}_m(i,j)$$

$${\mathcal{K}}_{\text{attr}}(i,j)=\exp (-\frac{||{\text{attr}}_i-{\text{attr}}_j|{|}^2}{2{\delta }_{\text{attr}}^2})$$

最后将累积的Gaussian进行体素化，每个体素的语义由Gaussian在空间中的线性加权计算。

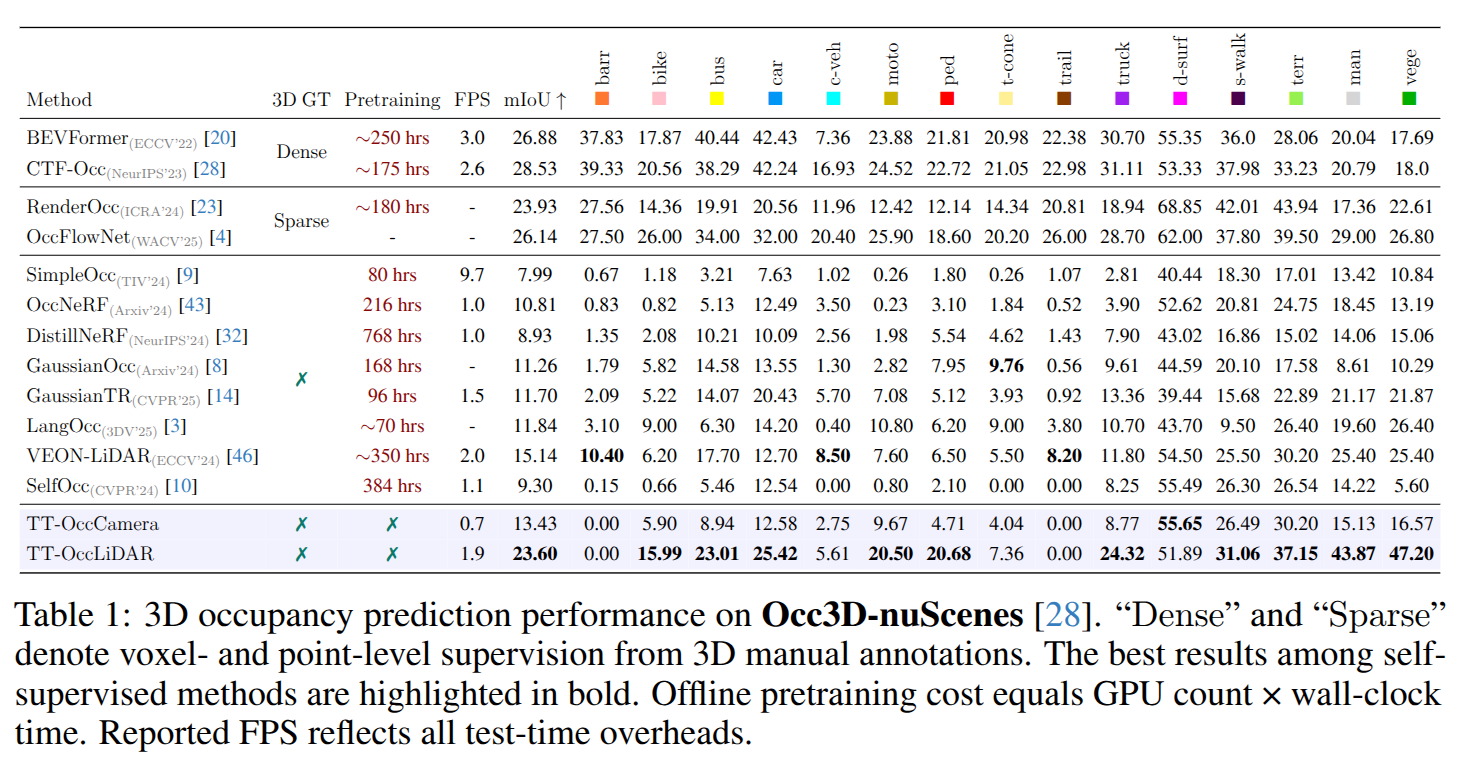
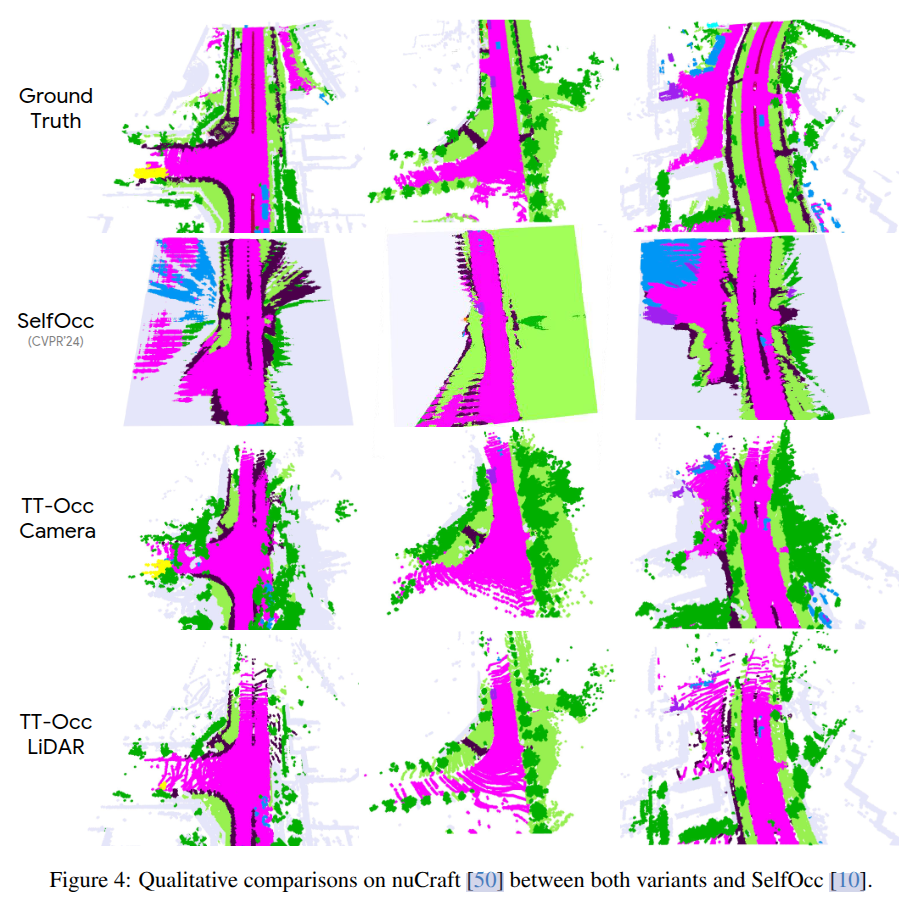
Experiments

砖

怎么说呢，一个有创新点但是应用价值有限的工作，展现了3DGS在OCC的应用方向和前景，越来越多的工作将VLM引入3D空间感知中，主要还是VLM背后数据的Scaling Law带来的降维打击，只可惜当前的精度还远没有达到应用的条件。