博客就应该是最自由传播的,不需要关注,不需要会员……
Neural Kernel Surface Reconstruction
https://research.nvidia.com/labs/toronto-ai/NKSR/
Abstract
本文提出了一种从大规模、稀疏和噪声点云重建 3D 隐式曲面的新方法。在神经核场(NKF)的基础上:1. 通过紧凑支持的核函数实现内存高效的稀疏线性求解器,从而实现大场景重建;2. 通过梯度拟合求解实现噪音鲁棒; 3. 降低了训练条件,可以使用任意数据集参与训练,甚至可以及混合不同尺度的对象和场景。
Introduction
3D重建的目的是从局部观测还原出完整的3D结构,本文的目的则是从稀疏的点云还原3D隐式曲面。挑战不仅在于大规模场景的点云数量庞大,且有传感器噪音,而且点是离散的,而表面是连续的。
然而,基于规则和显示公式计算的方法对于高噪声或稀疏输入的效果不佳,而基于模型数据驱动的方法缺难以推广到域外数据。这说明基于学习的方法受到数据集的约束,并且训练速度慢的问题也导致了数据集规模的提升困难,并且许多方法依赖于数据前处理来提取所需要的监督信息。这也阻碍了跨数据集泛化训练。
NKF为解决3D重建泛化问题提供了新的范式,NKF会学习一个数据相关的核,并且预测一个连续的占据场,作为该核在输入点上支持的线性组合。NKF的关键在于对核的显式编码,并且在测试时确保输出的插值结果是满足输入数据约束的。因此通过对不同形状的数据进行训练,NKF可以学习到3D重建问题的良好的归纳偏差,而不是针对特定数据。
- 首先,由于其使用的是全局核函数,NKF需要求解一个稠密的线性系统,并且其重建点云输入不能超过10000个点;
- 由于噪音也会占据约束位置,因此NKF抗噪音的能力较弱。
本文在NKF的基础上,
- 提出了一种新的、基于梯度的核函数,对噪音有更好的鲁棒性;
- 使用显式的层级体素结构,并使用支持密集运算的核来确保插值数据和不同尺度输出的一致性问题。
进而可以实现:

- 可以实现域外输入,即便是输入离散或是存在噪声,都生成高保真的重建结果;
- 可以在不同的数据集进行联合训练,并且只需要稠密的法向量进行监督,从而实现了训练数据的量变;
- 输入的点云数量可以很大很大。
Methodology
带有法向信息的点云作为输入,将预测的表面结果编码为NKF的零水平集,即一个隐式函数,该函数表示为一组经学习得到的、正定基函数的加权和;这些基函数以输入为条件,其权重在前向传播过程中通过线性优化计算得出。
这些基函数定义在一个稀疏体素层级结构上,该结构由我们通过一个稀疏卷积网络从输入点云中预测得到,并且每个基函数依赖于各体素顶点处插值得到的特征。
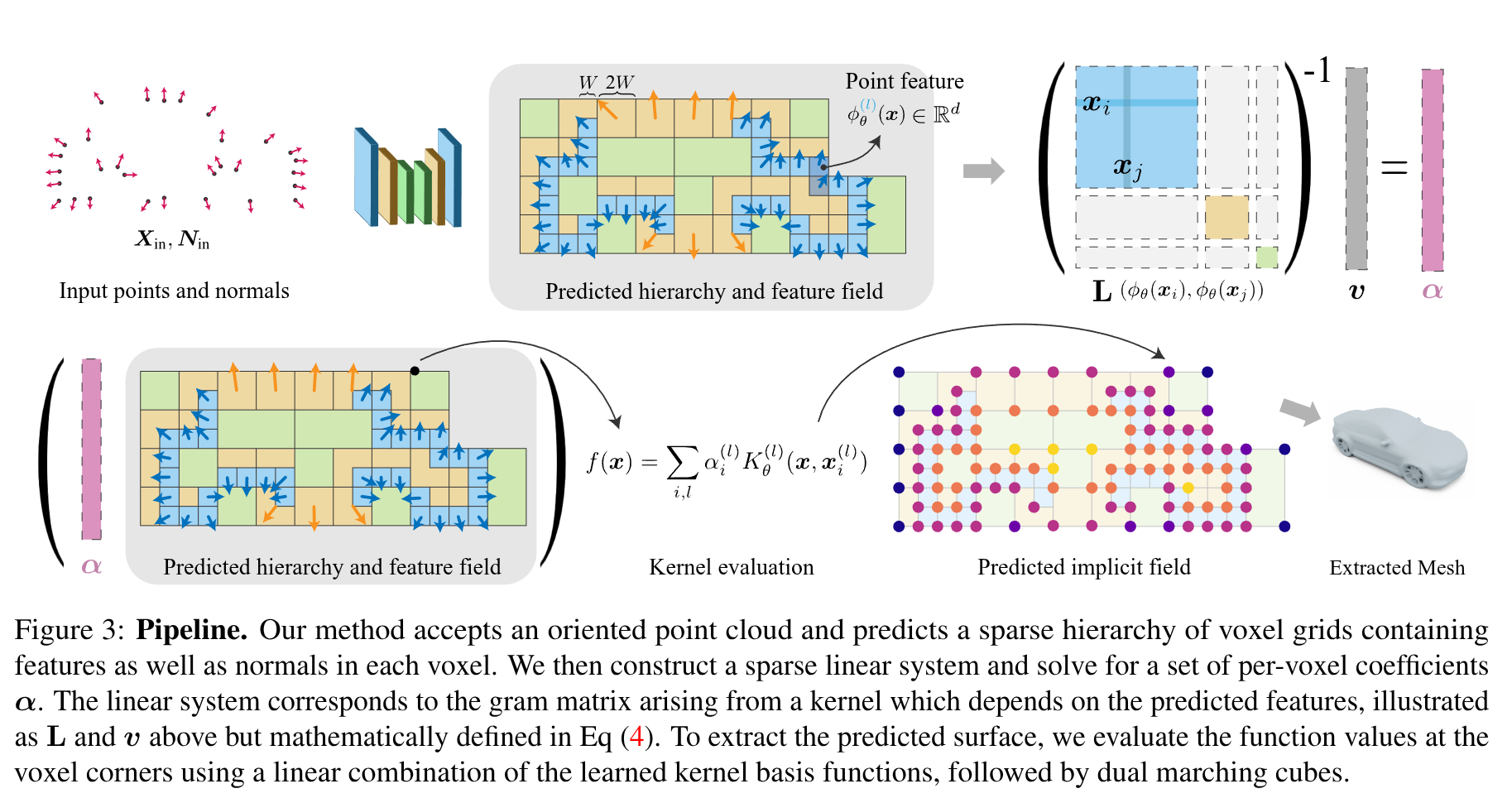
Predicting a 3D Shape from Points
基于输入的点云及其法向量,模型的前向传递会以可学习核函数的权重和的形式预测隐式表面:
-
先利用离散卷积模型预测体素结构,并包含每个体素的顶点特征,这些特征定义了那些以体素为中心的可学习基函数的集合;
-
通过求解一个线性系统来找到这些基函数的一组权重,该系统鼓励预测的隐式场在输入点附近有一个零值,并且具有与输入法线一致的梯度;
-
模型还可以预测几何的掩码,用于输出空间中哪些部分可以提取出最终的表面,修建虚假的几何。
-
Predicting a Sparse Voxel Hierarchy
输入带有法向量的点云和体素尺寸W,模型先使用离散卷积backbone处理L个体素,每个预测的体素分别包含了W,2W,2^L W……,且上一层级的体素中心点会包含在下一层级中。同时预测每个体素的特征ziu(l)z_iu^{(l)}ziu(l) 和对应的法向量,其中ziu(l)z_iu^{(l)}ziu(l)用于预测特征场ϕθ(l)(x∣Xin,Nin)\phi_{\theta}^{(l)} (x| X_{in}, N_{in})ϕθ(l)(x∣Xin,Nin),其通过贝塞尔插值和MLP将3维点映射到d-维特征空间中。1.Point Encoder
对于每个voxel,采用残差PointNet结构对点进行编码:
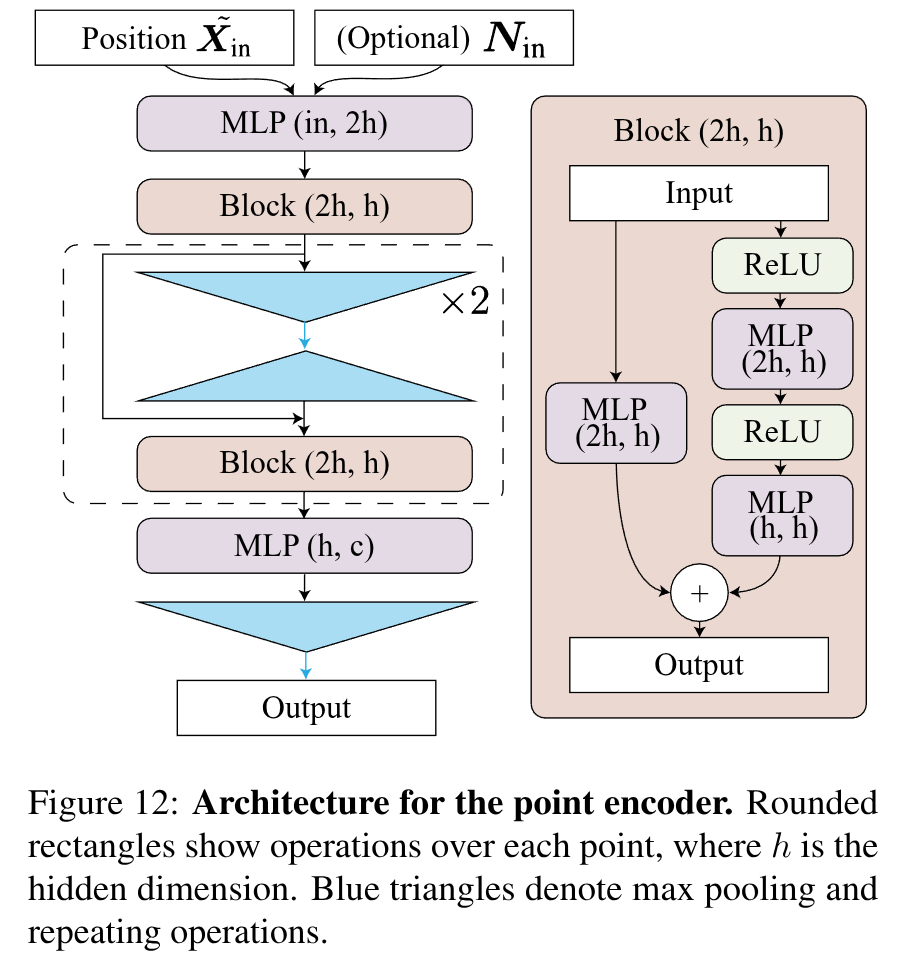
,同时为了消除坐标方差,将点云坐标转换到体素内的局部坐标系下作为输入Xˉin\bar{X}_{in}Xˉin,绝大部分数据集都会提供法向量作为额外信息来消除方向歧义,法向信息无需非常准确且很容易通过与传感器的相对位置得到。- U-Net Encoder
在将点云特征编码为体素特征后,使用一系列带有最大池化的离散卷积层来得到更宽泛的体素特征:
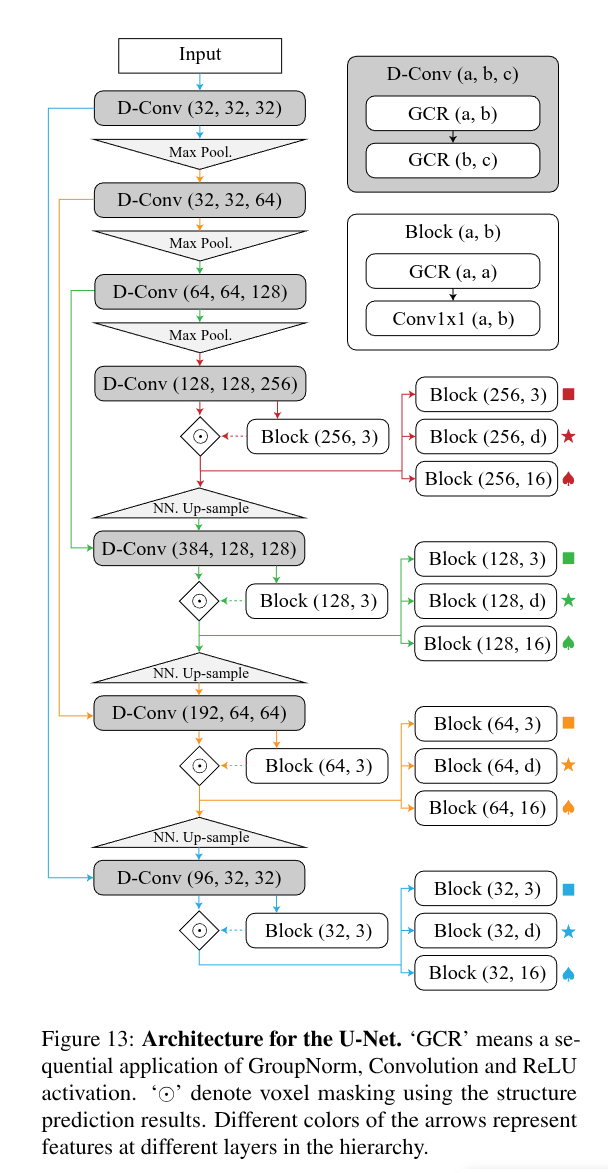
- U-Net Decoder
作为离散U-Ner结构的解码器,对影地,使用一系列带有最近邻上采样的卷积层,并添加一些short-cutting模块实现多尺度融合,每层都会有对应的任务分支,这些特征回归以下过程中所需的以下属性:
a. 结构预测分支输出三维特征来确定输出层级的结构;
b. 法向量预测分支输出三个维度的法向量结果,并输入到后续的线性系统中。并且该分支没有显式的监督信息,但本文发现法向信息的引入可以得到更好的结果。
c. 核函数预测分支输出特征ziu(l)z_iu^{(l)}ziu(l), 该特征用于预测隐式场,该特征通过MLP+贝塞尔插值可以获得任意位置的核场函数。
d. 掩码预测分支输出一个16维度的特征,然后通过MLP转换为标量,该MLP确定查询位置是否远离表面。- Structure Prediction
将结构预测分支的3维特征作为每个体素3种分类分数, 基于分类,体素将以不同的方式处理并完全形成一个预测的新层次结构,以保证更精细的体素定义的区域总是被较粗的体素覆盖。这些分类的语义如下:
a. Subdivide: 该体素应该被进一步分割为8(=2^3)个子体素;
b. Keep-as-is:该体素应该被保留当前结构
c. Delete: 该体素应该被删除
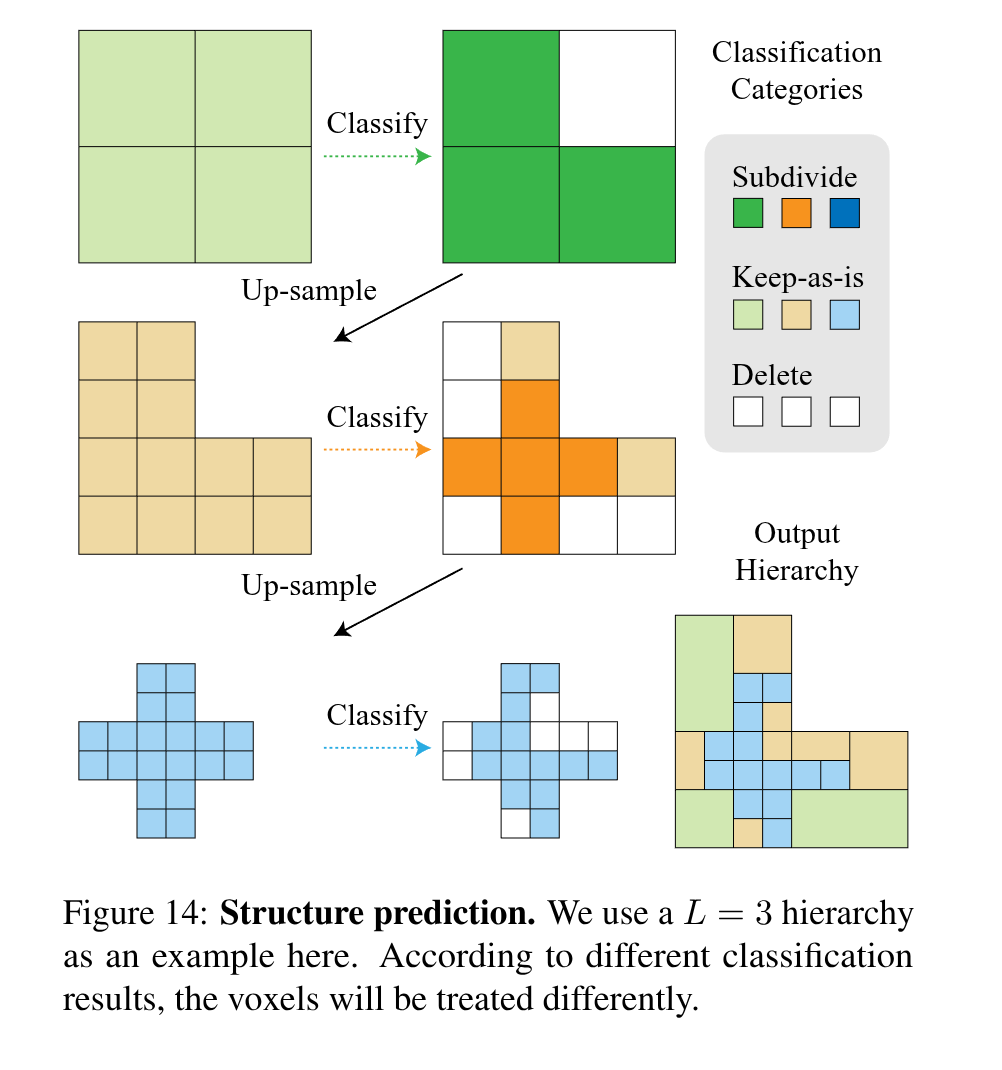
并且体素的层级结构是动态调整的,其他分支的预测结果都基于当前存在的体素结构
-
Sparse Neural Kernel Field Hierarchy
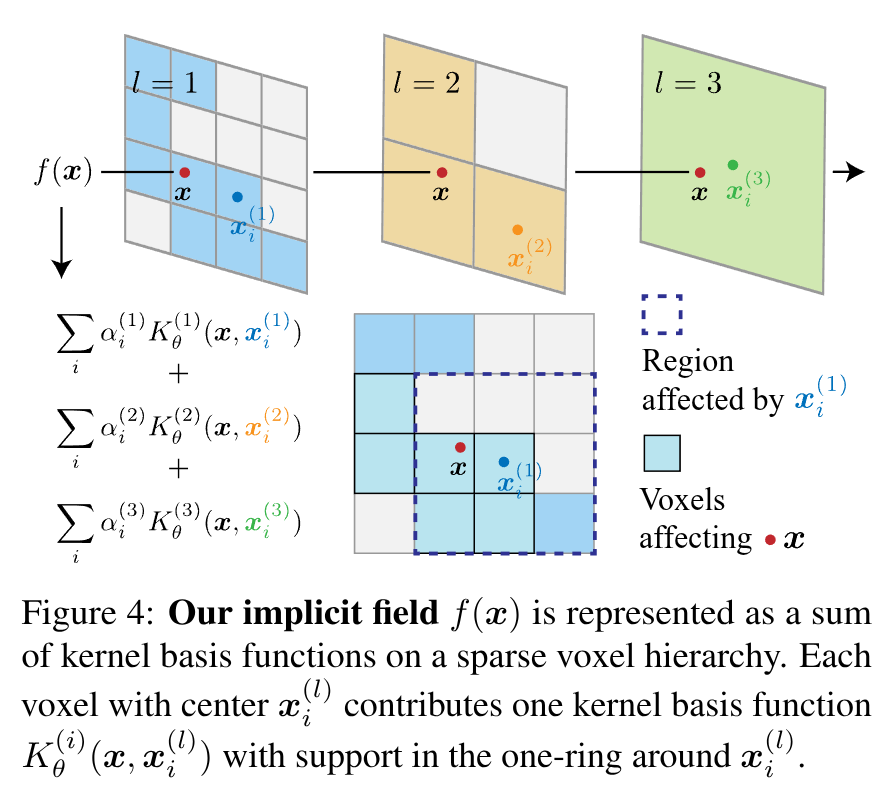
本文将预测的表面结果编码为NKF的零水平集,即一个隐式函数,该函数表示为一组经学习得到的、正定基函数的加权和,这些核函数以输入为条件,以处理后的体素中点为中心:
fθ(x∣Xin,Nin)=∑i,lαi(l)Kθ(l)(x,xi(l)∣Xin,Nin)f_\theta (x|X_{in}, N_{in}) = \sum_{i,l}\alpha_i^{(l)} K_{\theta}^{(l)} (x, x_i^{(l)}|X_{in}, N_{in}) fθ(x∣Xin,Nin)=i,l∑αi(l)Kθ(l)(x,xi(l)∣Xin,Nin)
其中,αi(l)\alpha_i^{(l)}αi(l)为对应层级中的对应体素标量权重,$ K_{\theta}^{(l)}$为对应层级中的预测核函数:
Kθ(l)(x,xi′)=<ϕθ(l)(x;Xin,Nin),ϕθ(l)(x′;Xin,Nin)>⋅Kb(l)(x,xi′) K_{\theta}^{(l)}(x, x_i^{'}) = <\phi_{\theta}^{(l)}(x;X_{in}, N_{in}), \phi_{\theta}^{(l)}(x';X_{in}, N_{in})> \cdot K_{b}^{(l)}(x, x_i^{'}) Kθ(l)(x,xi′)=<ϕθ(l)(x;Xin,Nin),ϕθ(l)(x′;Xin,Nin)>⋅Kb(l)(x,xi′)
其中,Kb(l):R3×R3→RK_{b}^{(l)}: \mathbb{R}^3 \times \mathbb{R}^3 \rightarrow \mathbb{R}Kb(l):R3×R3→R为贝塞尔核:在一个体素到其周围衰减为0
Kb(l)(x,x′)=ψ2(xx−xx′2l−1W)⋅ψ2(xy−xy′2l−1W)⋅ψ2(xz−xz′2l−1W)K_b^{(l)}(\mathbf{x}, \mathbf{x}') = \psi^2\left(\frac{x_x - x_x'}{2^{l-1}W}\right) \cdot \psi^2\left(\frac{x_y - x_y'}{2^{l-1}W}\right) \cdot \psi^2\left(\frac{x_z - x_z'}{2^{l-1}W}\right)Kb(l)(x,x′)=ψ2(2l−1Wxx−xx′)⋅ψ2(2l−1Wxy−xy′)⋅ψ2(2l−1Wxz−xz′)
其中,ψ2:R→R\psi^2: \mathbb{R} \rightarrow \mathbb{R}ψ2:R→R为单变量二阶b样条:
ψ2(s)={(s+32)2if s∈[−32,−12]−2s2+32if s∈[−12,12](s−32)2if s∈[12,32]0otherwise\psi^2(s) =
\begin{cases}
\left(s + \dfrac{3}{2}\right)^2 & \text{if } s \in \left[-\dfrac{3}{2}, -\dfrac{1}{2}\right] \\
-2s^2 + \dfrac{3}{2} & \text{if } s \in \left[-\dfrac{1}{2}, \dfrac{1}{2}\right] \\
\left(s - \dfrac{3}{2}\right)^2 & \text{if } s \in \left[\dfrac{1}{2}, \dfrac{3}{2}\right] \\
0 & \text{otherwise}
\end{cases}ψ2(s)=⎩⎨⎧(s+23)2−2s2+23(s−23)20if s∈[−23,−21]if s∈[−21,21]if s∈[21,23]otherwise
- Computing a 3D implicit surface from points
基于已有的多层级体素结构,可学习的核函数和法向量,本文通过为核场找到最优参数α∗={{αi(l)}l=1L}i=1n(l)\alpha^{*}=\{ \{ \alpha_i^{(l)}\}_{l=1}^{L} \}_{i=1}^{n^{(l)}}α∗={{αi(l)}l=1L}i=1n(l)来计算隐式曲面。我们通过在模型的前向传递中精确地最小化以下损失来找到这些系数:
α∗=arg minαi(l)∑l=1L′∑i=1n(l)∥∇xfθ(xi(l))−ni(l)∥22+∑j=1nin∣fθ(xjin)∣2\boldsymbol{\alpha}^* = \argmin_{\alpha_i^{(l)}} \sum_{l=1}^{L'} \sum_{i=1}^{n^{(l)}} \left\| \nabla_{\mathbf{x}} f_\theta(\mathbf{x}_i^{(l)}) - \mathbf{n}_i^{(l)} \right\|_2^2 + \sum_{j=1}^{n_{\mathrm{in}}} \left| f_\theta(\mathbf{x}_j^{\mathrm{in}}) \right|^2α∗=αi(l)argminl=1∑L′i=1∑n(l)∇xfθ(xi(l))−ni(l)22+j=1∑ninfθ(xjin)2
通过最小化该损失,我们希望神经核场函数可以具备与体素中心的法向量一致的梯度,并且预测的隐式场在输入点附近应该有零值。
- Masking module
预测的神经核场是定义在整个体素空间上的,但是一些粗粒度且远离表面的体素可以包含并不需要的几何信息。因此,本文引入了一个掩码模块,该模块将预测的核场函数限制在输入点附近,并使用一个MLP来预测该区域中的掩码。只使用分数大于0.5的掩码区域,以获得更好的结果。
Supervision
在训练阶段,需要对应的点云和法向量作为输入,以及相对应的稠密点云和法向量真值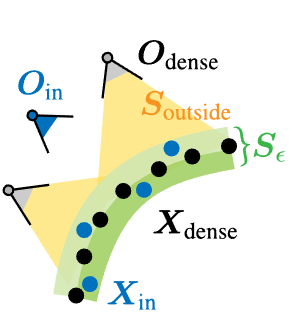
Experiments


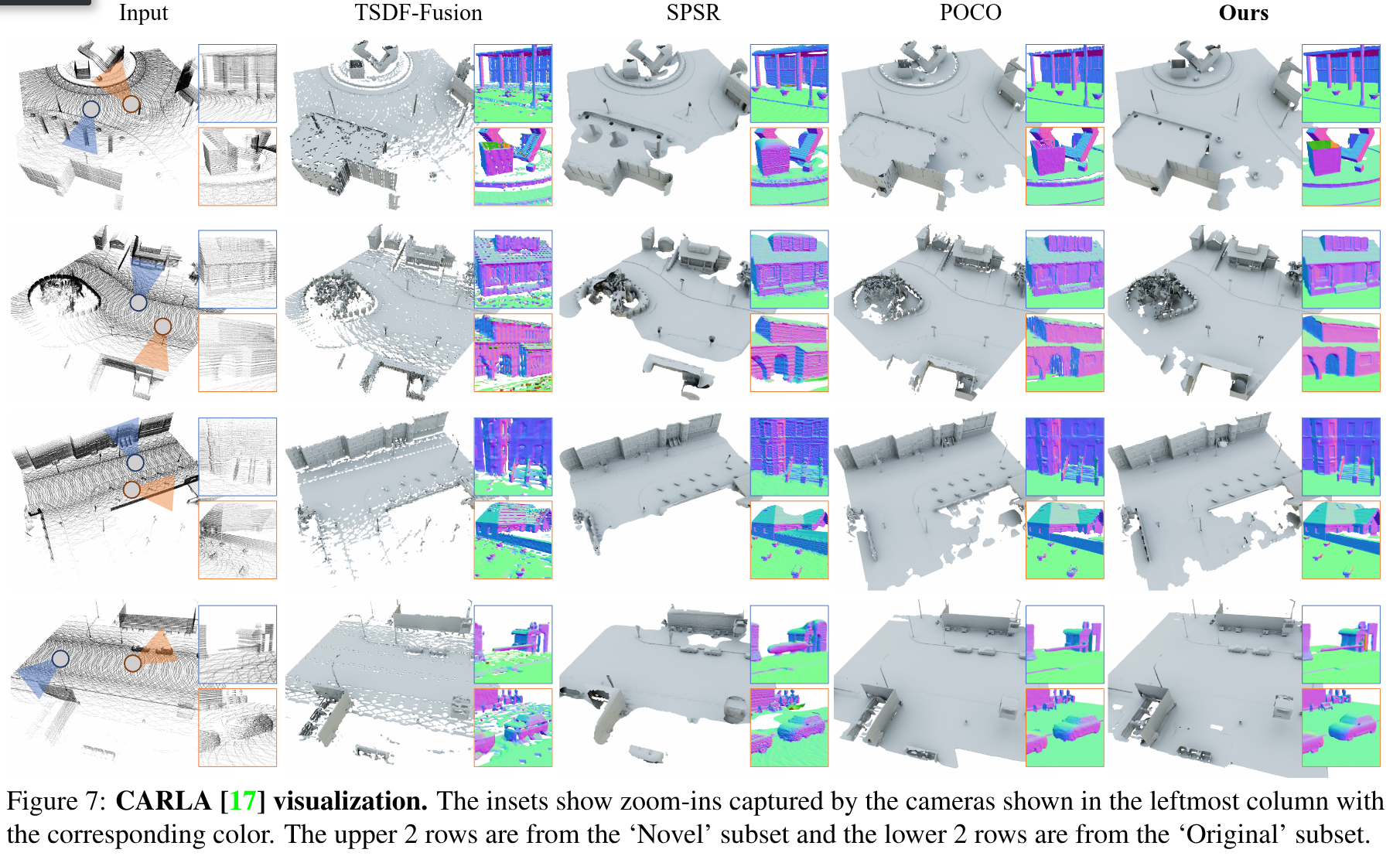
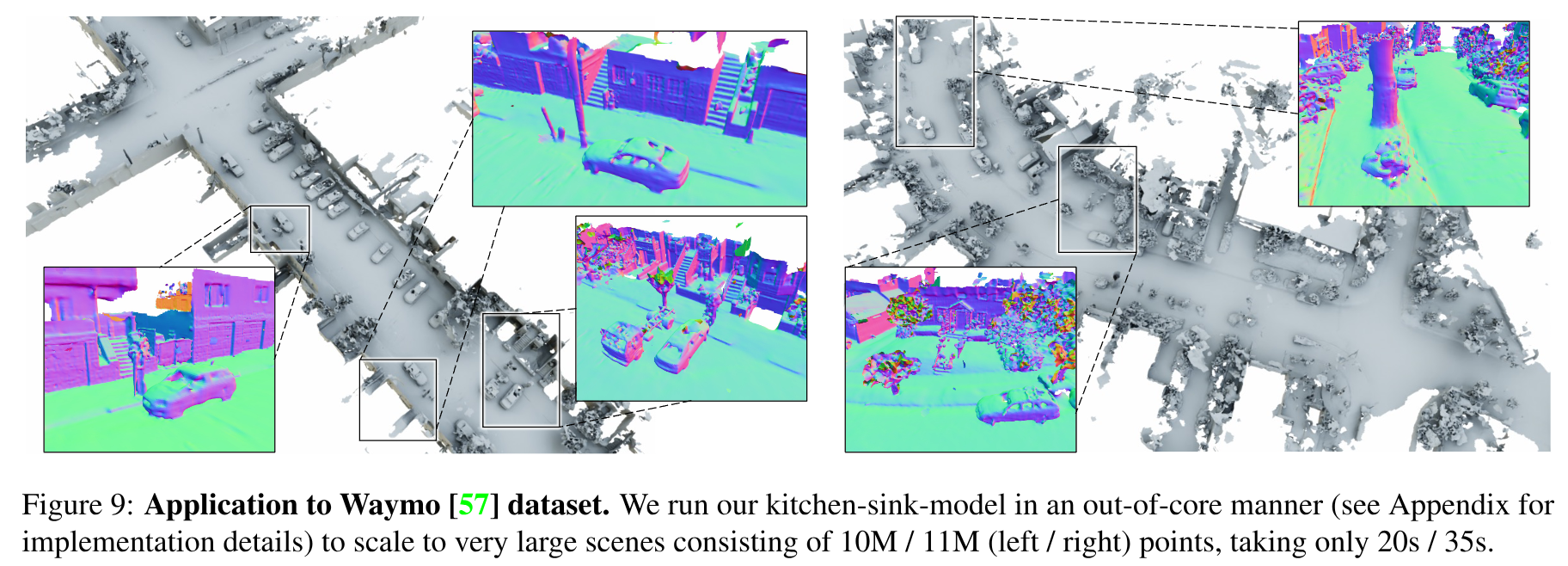
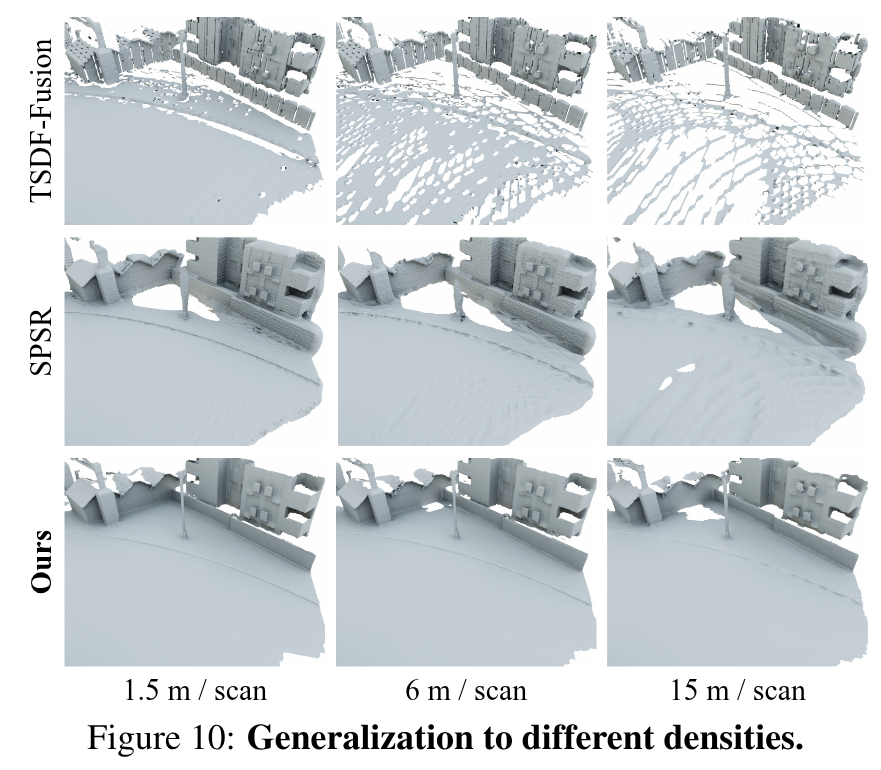
 基于神经核场的大规模3D重建
基于神经核场的大规模3D重建




















 988
988

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








