KMP算法-DFA版本

一、暴力法

为了更好地理解KMP算法，我们先来看看朴素的暴力法是如何执行的。

设待匹配的字符串为ABABABABAC，模式串为ABABAC，i为字符串下标，j为模式串下标

首先取i=0，遍历一遍j，直到出现不匹配：

ABABABABAC

ABABAC

 然后取i=1，遍历一遍j，直到出现不匹配：

ABABABABAC

  ABABAC

然后取i=2，遍历一遍j，直到出现不匹配：

ABABABABAC

     ABABAC

……

不难发现，这种暴力法的缺点：做了很多无用功，从i往后已经走了很多步了，但是每次i还是只能退回去。

二、“滑动条带”的思想

如果把模式串想象成两个重叠在一起的透明条带，滑动其中一个 ，直到与另一个部分完全重合。

像这样：（以i=2时为例）

ABABABABAC

     ABABAC

->       ABABAC

这样，i就不用动了，直接把j调整为4，继续匹配

具体“滑动”到什么位置（把j调整到什么位置），可以事先计算好，这就要说到DFA了

三、DFA

图中，每个圆圈都是一个状态，圆圈中的数字表示已经匹配好的字符个数，箭头表示了状态转移的方式，箭头上的字母表示下一个出现的字母是什么。状态怎么转移，已经通过“滑动窗口”定义好了，于是DFA也就定义好了。

可以证明，如果每一步都遵循DFA来走，那么在任意时刻，能匹配到的字符串都是最长的。（证明：如若不然，必然存在某个时刻t，使得t-1时刻是最长的，t时刻不是最长的，那么就违背了滑动窗口的定义）

这一点很关键，在接下来DFA生成的部分会用到。

现在先不管DFA是怎么高效生成的，既然我们已经可以用笨方法（滑动窗口）来生成DFA了。

假设我们已经有了DFA，那么代码就可以这么写：

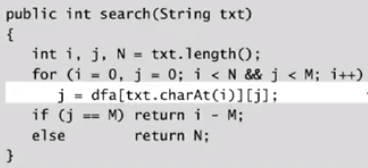
（由于i不会回退，我们可以一边读数据一边处理：

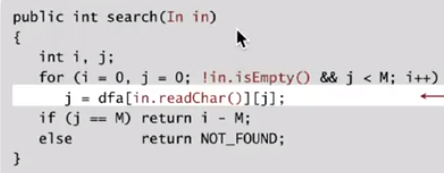
可见有了DFA，还是非常高效的。i不会回退，因此可以在O（待匹配字符串长度）的时间内完成匹配。

但是，DFA的生成会不会拖后腿呢？

四、DFA的生成（核心）

原理部分，我们可以这样理解：

首先用“一次性完美匹配”的情况来构建DFA的骨架

接下来的问题是：在状态j（意即：已经成功匹配了j个字符，也就是模式串中下标为0~j-1的字符），如果在下一步出现了不匹配，该跳转到哪里？

设待匹配字符串中，不匹配的那个字符为c。

目标是要滑动窗口，寻找最长的重叠字符串，换言之，要在 [ 下标为1~j-1的字符 + c ] 中匹配最长的字符串。等等，这个场景似曾相识，既然恰好j个字符（不会越界），那我们用当前的DFA半成品过一遍 [ 下标为1~j-1的字符 + c ] ，结果指向哪，我们就跳转到哪！

于是，生成DFA的代码如下：

代码中的X代表用半成品DFA过一遍 [ 下标为1~j-1的字符 ]（没有c）的结果

复杂度如图所示，没怎么拖后腿

 

PS：还有一种NFA版本的KMP算法，更为常见一些，改天再研究