矩阵的乘法
矩阵对向量可以做拉伸也可以做旋转

对角矩阵对向量(x,y)(x,y)(x,y)在x轴上拉伸了3倍。非对角矩阵对向量(x,y)(x,y)(x,y)不仅做了拉伸,同时也做了旋转。
特征值和特征向量到底描述了什么
举个例子:打拳击。我们可以把方向当做特征向量,在这个方向上用多大的力量就是特征值。
特征向量可以说是主要的前进目标,特征值是向这个目标产生多大的作用。
数学定义
对于给定矩阵A,寻找一个常数λ\lambdaλ和非零向量xxx,使得向量xxx被矩阵A作用后所得的向量AxAxAx与原向量xxx平行,并且满足Ax=λxAx=\lambda xAx=λx。如下图所示:
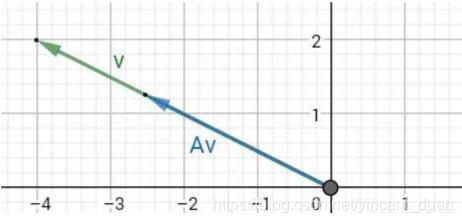
λ\lambdaλ就是特征值,xxx就是特征值λ\lambdaλ对应的特征向量。
例如要做降维操作,10维的数据,每一维度都有一个特征向量,有下面两个维度逇特征向量,应该选择哪一个?

如果有两个特征值λ1>λ2\lambda_1 > \lambda_2λ1>λ2,我们会认为λ1\lambda_1λ1对应的特征向量更重要,更有价值,所以在做降维操作时,选择特征值大的一个特征向量。
特征空间
特征空间包含了所有的特征向量。
应用
既然特征值表达了重要程度,并且和特征向量所对应,那么特征值大的就是主要信息了,基于这一点,我们可以提取各种有价值的信息了!

图像可以看做是一个矩阵,既然是矩阵,就可以算出这个矩阵的特征向量和特征值,我们如果取前10个特征值最大的特征向量,那么就可以对这个图像进行压缩,虽然图像变的有一些模糊,但是整体不会有太大变化。
使用numpy计算特征值和特征向量
import numpy as np
# 创建矩阵 维度 4*2
data = np.array([[2, 4], [1, 3], [0, 0], [0, 0]])
# 将矩阵转为方阵 维度 4*4
A = np.dot(data, data.T)
#A=array([[20, 14, 0, 0],
# [14, 10, 0, 0],
# [ 0, 0, 0, 0],
# [ 0, 0, 0, 0]])
# 求A的特征值和特征向量
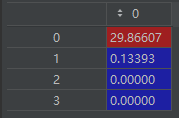
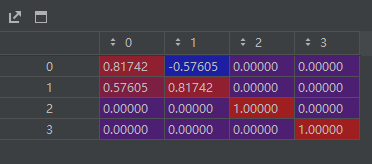
val,vector = np.linalg.eig(A)
# val=array([29.86606875, 0.13393125, 0. , 0. ])
# vector=array([[ 0.81741556, -0.57604844, 0. , 0. ],
# [ 0.57604844, 0.81741556, 0. , 0. ],
# [ 0. , 0. , 1. , 0. ],
# [ 0. , 0. , 0. , 1. ]])
特征值29.86606875 对应的
特征值29.86606875 对应的特征向量为[ 0.81741556,0.57604844,0 ,0]
特征值0.13393125对应的特征向量为[-0.57604844,0.81741556,0,0]
验证:
np.dot(A, vector[:,0])
# array([24.41298932, 17.20430221, 0. , 0. ])
np.dot(val[0], vector[:,0])
# array([24.41298932, 17.20430221, 0. , 0. ])
np.dot(A, vector[:,1])
# array([-0.07715089, 0.10947749, 0. , 0. ])
np.dot(vector[:, 1], val[1])
array([-0.07715089, 0.10947749, 0. , 0. ])
矩阵data:

矩阵A:

特征值:
特征向量:





 博客介绍了特征值和特征向量的概念及其在矩阵运算中的作用,如向量的拉伸和旋转。特征值描述了矩阵作用下向量的变化程度,而特征向量则指示了主要变化的方向。在降维操作中,选择具有较大特征值的特征向量可以保留主要信息。通过numpy计算矩阵的特征值和特征向量,可以实现图像的压缩,尽管可能会导致轻微模糊,但能保持基本内容。
博客介绍了特征值和特征向量的概念及其在矩阵运算中的作用,如向量的拉伸和旋转。特征值描述了矩阵作用下向量的变化程度,而特征向量则指示了主要变化的方向。在降维操作中,选择具有较大特征值的特征向量可以保留主要信息。通过numpy计算矩阵的特征值和特征向量,可以实现图像的压缩,尽管可能会导致轻微模糊,但能保持基本内容。
















 3459
3459

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








