EMA 滤波（指数移动平均滤波）

EMA 滤波（指数移动平均滤波）是常用的时域平滑滤波方法

关键特点

• 计算高效，仅需保存上一时刻结果，无需缓存历史数据。
• 兼顾响应速度与平滑效果，通过调整α可灵活适配场景。
• 对突发噪声的抑制能力中等，更适合处理平稳变化的信号。

动态系统视角：状态更新方程

EMA 公式也可以看作是一个状态空间模型中最简单的状态更新：

状态估计=新观测×信任度+旧估计×(1−信任度)

这和卡尔曼滤波（Kalman Filter）的更新思想类似——只不过 EMA 用了固定的信任度 α ，而卡尔曼滤波会动态调整。

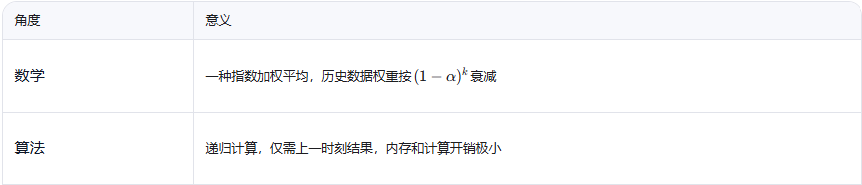
一句话概括 EMA 公式的意义：

它用一种计算高效、记忆衰减的方式，将当前观测与历史经验融合，得到一个更稳健、平滑的估计值。

变形公式

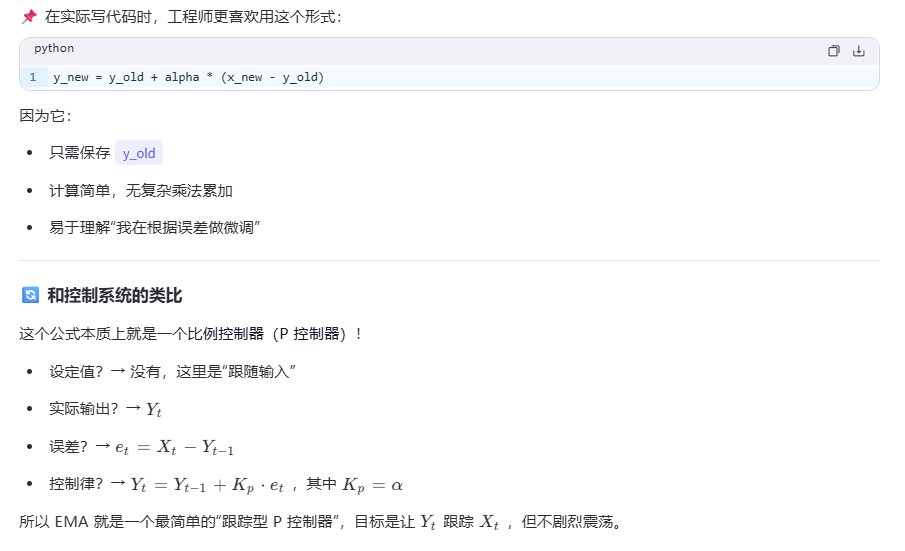
总结：EMA 公式的多重意义与应用价值

加权平均视角	对历史数据进行指数衰减加权平均，突出近期趋势	统计分析、信号处理	理论严谨，便于频域分析
修正量视角	基于误差的动态修正过程，平衡新旧认知	嵌入式开发、控制系统、机器学习	直观易懂，易于实现与调试
物理系统类比	等效于一阶低通滤波器或 RC 电路	电子工程、自动控制	提供物理直觉，便于系统建模
工程实现视角	递归状态更新，仅需一个变量	实时系统、物联网、边缘计算	计算高效，资源占用极小

✅ 综合结论：
EMA 公式是一个高度浓缩的智能滤波器，它既体现了数学上的优雅（指数加权），又蕴含了工程上的实用（误差驱动）。无论从哪个角度切入，都能看到其在“平衡噪声抑制与响应速度”方面的卓越能力。

下面给出一份EMA 滤波 Python 实现代码例子

import numpy as np
import matplotlib.pyplot as plt
#中文显示标题
plt.rcParams['font.sans-serif'] = ['SimHei']

class EMAFilter:
    """指数移动平均滤波器"""

    def __init__(self, alpha=0.3):
        """
        初始化滤波器
        :param alpha: 平滑系数（0 < alpha < 1），值越大响应越快，平滑性越差
        """
        self.alpha = alpha
        self.last_output = None  # 保存上一时刻的滤波结果

    def filter(self, x):
        """
        对单个数据点进行滤波
        :param x: 当前输入数据
        :return: 滤波后的数据
        """
        if self.last_output is None:
            # 首次输入时，直接将输入作为初始输出
            self.last_output = x
        else:
            # EMA核心公式：当前输出 =  alpha*当前输入 + (1-alpha)*上一时刻输出
            self.last_output = self.alpha * x + (1 - self.alpha) * self.last_output
        return self.last_output

    def reset(self):
        """重置滤波器状态"""
        self.last_output = None


# 生成测试数据（含噪声的正弦波）
def generate_test_data():
    # 生成时间序列（0到10秒，共1000个点）
    t = np.linspace(0, 10, 1000)
    # 原始信号（正弦波）
    signal = np.sin(t)
    # 添加高斯噪声（均值0，标准差0.5）
    noise = np.random.normal(0, 0.5, size=len(t))
    noisy_signal = signal + noise
    return t, signal, noisy_signal


# 主函数：测试不同alpha的滤波效果
def main():
    # 生成测试数据
    t, original_signal, noisy_signal = generate_test_data()

    # 定义不同的平滑系数（对比效果）
    alphas = [0.1, 0.3]
    filtered_results = {}

    # 对每个alpha进行滤波
    for alpha in alphas:
        ema_filter = EMAFilter(alpha=alpha)
        filtered = [ema_filter.filter(x) for x in noisy_signal]
        filtered_results[alpha] = filtered

    # 可视化结果
    plt.figure(figsize=(12, 6))
    plt.plot(t, original_signal, label='原始信号（无噪声）', linestyle='--', color='black')
    plt.plot(t, noisy_signal, label='含噪声信号', alpha=0.5, color='gray')

    # 绘制不同alpha的滤波结果
    colors = ['blue', 'green', 'red']
    for i, alpha in enumerate(alphas):
        plt.plot(t, filtered_results[alpha], label=f'EMA滤波 (α={alpha})', color=colors[i])

    plt.xlabel('时间')
    plt.ylabel('信号值')
    plt.title('EMA滤波效果对比')
    plt.legend()
    plt.grid(True)
    plt.show()


if __name__ == "__main__":
    main()

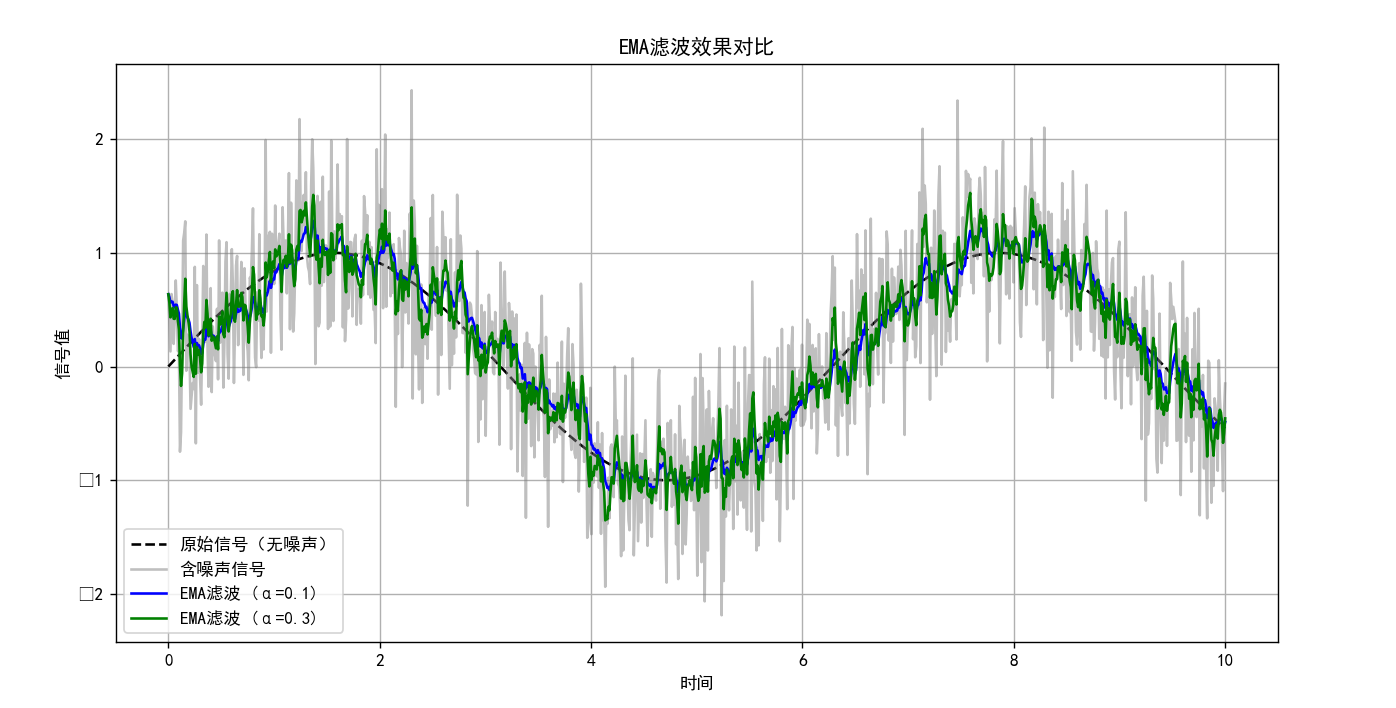
效果如下：