r a n k ( A A T ) = r a n k ( A ) rank(AA^T)=rank(A) rank(AAT)=rank(A),rank是矩阵的秩的意思。
投影矩阵有什么用?因为Ax=b很可能没有解,但是没有解我们可以求最接近的解啊。所以要把b投影到A的列向量空间中。为何要投影到A的向量空间中?因为Ax它的本质就是对A的列向量进行线性组合,而线性组合就是向量空间。如果我们能把b投影到A的向量空间中。
假设 A x ^ A\hat x Ax^是b在A列向量空间上的投影,那么 p = ( A x ^ − b ) p=(A\hat x-b) p=(Ax^−b),其中 p p p是误差向量。我们知道 A x ^ A\hat x Ax^是A的列向量空间中的一个向量,并且 A x ^ A\hat x Ax^是b在A列向量空间上的投影。那么 p = ( A x ^ − b ) p=(A\hat x-b) p=(Ax^−b)垂直于A的列向量空间。如下图所示:
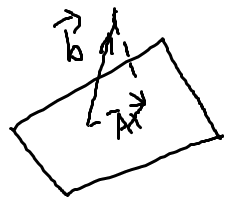
现在我们证明下 A T A x ^ = A T b A^TA \hat x=A^Tb ATAx^=ATb
根据 p = ( A x ^ − b ) p=(A\hat x-b) p=(Ax^−b)垂直于A的列向量空间,所以 A T ( A x ^ − b ) = 0 A^T(A\hat x-b)=0 AT(Ax^−b)=0,所以 A T A x ^ = A T b A^TA\hat x=A^Tb





 本文深入探讨了线性代数中的QR分解及其与Gram-schmidt正交法的关系,阐述了矩阵在电流图表示中的应用,解释了正交向量、子空间和最小二乘法的概念。通过实例说明行向量和列向量线性组合的含义,并讨论了最小二乘法在求解无解问题时的作用。
本文深入探讨了线性代数中的QR分解及其与Gram-schmidt正交法的关系,阐述了矩阵在电流图表示中的应用,解释了正交向量、子空间和最小二乘法的概念。通过实例说明行向量和列向量线性组合的含义,并讨论了最小二乘法在求解无解问题时的作用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2113
2113

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








