《数据结构》期末提纲之Huffman树

1.名词解释

• 路径与权
  从起始节点到目标节点所经过的分支序列为路径，所经分支数目为路径长，若给节点赋值，则称此值为权。
• 节点的带权路径长
  节点的带全路径唱等于该节点的权与根节点到该节点的路径长之积。
• 树的带权路径长(WPL)
  树的带权路径长为所有叶子节点的带权路径长之和。
• 图示（今天带了数位板就直接用笔画了（懒））
  

2.Huffman树简介

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。（百度百科）

3.Huffman树的构造

分为3步：
1）将每个节点视作一棵树，全部节点组成一个森林。
2）选取所有树中权值最小的两棵树，分别作为一个新节点的左子树与右子树，构成一棵新树，该树的权值为左右两棵子树权值之和。
3）重复步骤二直到仅剩一棵树，该树为所求Huffman树。
如图所示：

4.Huffman编码

比如说要传输一个由ABCDEF组成字符串，每个字母采用0与1编码，传统编码方式需要用到三位。假设要传输这样一个字符串：ABBBBCCDDDDDDDDEEEEEFFFFFFF，即六个字母出现次数分别为1、4、2、8、5、7时，按照传统编码方式需要传输81位。然而，并不是每个字母都要用到三位编码，而且传输位数越多成本越高。所以，需要用最少的位数传输这样的字符串，就要为每个字母重新编码。这种编码就叫做Huffman编码。
Huffman编码分为三部。首先按权值构造Huffman树，然后将该树所有节点与左孩子连接路径标0，与右孩子的标1，根到叶子节点的路径为叶子节点的Huffman编码。如图所示：（还是上面的例子）

对字符进行Huffman编码后，传输上述字符串仅用64位，明显少于传统编码的81位。

5.Huffman树及编码的实现

• 基本思路
  首先将各个节点按权值置于优先队列中，数值越小优先级越高。然后开始进行树的构建，每次出队两个节点，将这连个节点与一个新节点构成新树入队，重复以上操作直到队列中只有一个树，该树位Huffman树。将该树出队后，进行BFS并依次记录遍历路径，向左遍历为0，向右遍历为1，将路径存入叶子节点，输出叶子节点与路径，即Huffman编码。

• 设计问题
  处理一组数据，第一行为一个整数n，代表有n个数据需要处理，第二行到第n+1行每行两个数据，分别为一个字符与该字符在某个序列中出现次数。输出每个字符及其所对应的Huffman编码。

• 代码实现

#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define M 1000000007
using namespace std;
typedef long long LL;
const int maxn = 1e5+6;

char s[maxn];

struct node //节点结构体
{
    char data; //所存字符
    int weight; //所占权值
    queue<int> code; //Huffman编码
    node* l_child; //左孩子
    node* r_child; //右孩子
};

bool cmp(node* x,node* y)
{
    return x->weight > y->weight; //重定义比较
}

vector<node*> a; //充当优先队列

int main()
{
    int n; cin >> n;
    for(int i = 1;i <= n;++i) //输入每个节点信息并且进入数组
    {
        char c;
        int w;
        cin >> c >> w;
        node* tmp = new node;
        tmp->data = c;
        tmp->weight = w;
        tmp->l_child = NULL;
        tmp->r_child = NULL;
        a.push_back(tmp);
        sort(a.begin(),a.end(),cmp);
    }
    //以下为Huffman树构造
    while(a.size() > 1)
    {
        node *tmp1,*tmp2,*tmp;
        tmp = new node;
        tmp1 = a.back(); a.pop_back(); //每次弹出两个权值最小的节点
        tmp2 = a.back(); a.pop_back();
        tmp->l_child = tmp1; //构造新的树
        tmp->r_child = tmp2;
        tmp->weight = tmp1->weight + tmp2->weight;
        a.push_back(tmp); //将新的树存入数组并排序
        sort(a.begin(),a.end(),cmp);
    }
    node* huffman = a.back(); a.pop_back(); //弹出仅剩的一个树，即Huffman树
    //以下为对Huffman树的广度优先遍历
    queue<node*> q2; //BFS队列
    q2.push(huffman);
    while(!q2.empty())
    {
        node* now = q2.front(); q2.pop();
        if(now->l_child == NULL && now->r_child == NULL) //当前节点为叶子节点时
        {
            cout << now->data << ": "; //输出字符
            while(!now->code.empty()) //输出Huffman编码
            {
                cout << now->code.front();
                now->code.pop();
            }
            cout << endl;
        }
        if(now->l_child != NULL) //存在左孩子时
        {
            now->l_child->code = now->code; //左孩子节点Huffman编码为当前节点加一个0
            now->l_child->code.push(0);
            q2.push(now->l_child);
        }
        if(now->r_child != NULL)
        {
            now->r_child->code = now->code; //右孩子节点Huffman编码为当前节点加一个1
            now->r_child->code.push(1);
            q2.push(now->r_child);
        }
    }

    return 0;
}

• 运行结果
  
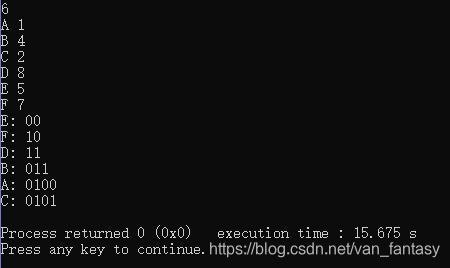
• 说明
  每个节点的Huffman编码不唯一，但是编码长度唯一，Huffman树的WPL唯一。

相关链接：
二叉树：传送门
BFS：传送门（未写）

总提纲：《数据结构》期末提纲小结