数据结构之哈夫曼树的实现

1、Huffman(哈夫曼)树的一些基本概念

1、1哈夫曼树的定义

最简哈夫曼树是一种数据结构，是由德国数学家冯·哈夫曼发现的，又称最优二叉树，是一种带权路径长最短的树。所以Huffman树是一种二叉树。

1、2哈夫曼树的经典应用

哈夫曼树最经典的应用时在通信领域的哈夫曼编码上面。经哈夫曼编码的信息消除了冗余的数据，加提高了通信信道的传输效率，目前，Huffman编码计数还是数据压缩的重要方法。关于Huffman编码的具体介绍与实现，我觉得这篇文章写的很相信，也很容易理解，感兴趣的读者也可以阅读一下Huffman编码的具体介绍与实现。

1、1关于路径长度

路径（path） 是树中一个结点到另一个结点之间的分支构成该两结点之间的路径。路径长度（path length）是指路径上的分支条数。树的路径长度是树的根节点到每一个结点的路径长度之和。

根据树的定义可以清楚的知道，从树的根结点到达树中每一结点有且仅有一条路径。若设树的根节点处于第一层，某一结点处于第k层，因为从根节点到达这个结点的路径上的分支条数为k-1,所以有：从根节点到其他各节点的路径长度等于该结点所处的层次k-1。

二叉树中，如果想要树的路径长度（根节点到各结点的路径长度之和）达到最小，那么该二叉树一定是完全二叉树或者理想平衡二叉树。

带权路径长度：在一棵树中，如果其结点上附带有一个权值，通常把该结点的路径长度与该结点上的权值之积称为该结点的带权路径长度（weighted path length）。树的带权路径长度：如果树中每个叶子上都带有一个权值，则把树中所有叶子的带权路径长度之和称为树的带权路径长度。设某二叉树有n个带权值的叶子结点，则该二叉树的带权路径长度记为：

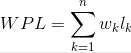
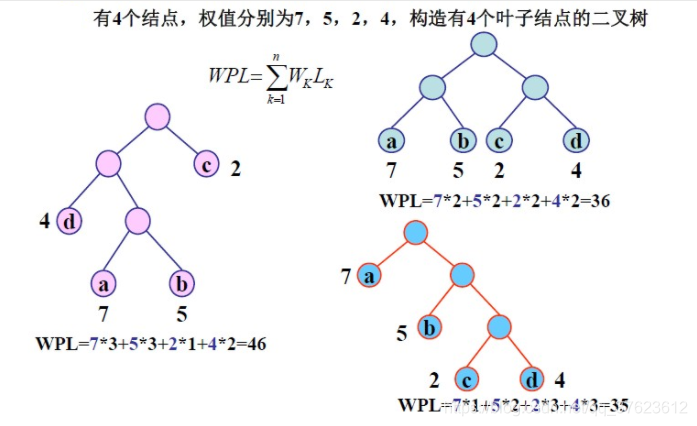
一般来说，用n（n>0）个带权值的叶子来构造二叉树，限定二叉树中除了这n个叶子外只能出现度为2的结点。那么符合这样条件的二叉树往往可构造出许多颗，其中带权路径长度最小的二叉树就称为哈夫曼树或最优二叉树。

2、Huffman树的构造过程

为了构造权值集合为{w1, w2, ..., wn}的Huffman树，Huffman提出了一个构造算法，这个算法称之为Huffman树。其基本思路为：

（1）根据跟定的n各权值{w1, w2, ..., wn}，构造具有n棵扩充二叉树的森林F = {T1, T2, ...Tn}，其中每棵扩充二叉树Ti只有一个权值wi的根节点，其左右子树均为空。

（2）重复一下步骤，知道F中仅剩下一棵树为止：

1. 在F中选取两棵根结点的权值最小的扩充二叉树，作为左、右子树构造义一棵新的二叉树。置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
2. 在F中删去这两棵二叉树。
3. 把新的二叉树加入F。

例如，设给定的权值集合为{7， 5， 2， 4}，构造Huffman树的过程下图所示。首先构造每棵树只有一个结点的森林，参看图(a)；然后每次选择两个根结点权值最小的扩充二叉树，以他们的左、右子树构造新的扩充二叉树，步骤参看(b)，(c)，（d），最后得到一棵扩充二叉树。

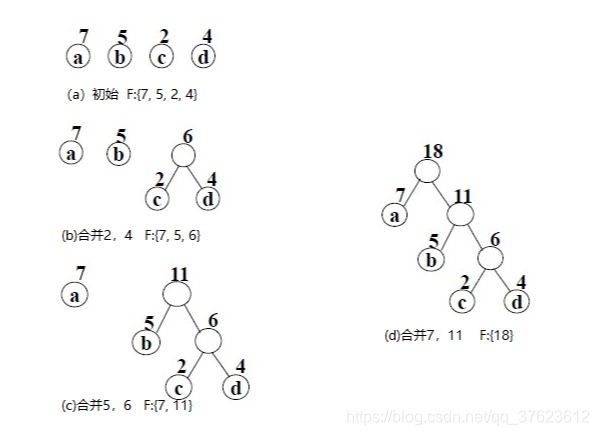
因为在构建Huffman树的时候需要删去最小权值的树，插入新树的过程，这个过程与最小堆的作用是一致的，利用最小堆可以方便的实现Huffman树的构造，大家如果对最小堆的概念及实现过程感兴趣的话可以看我的上一篇文章数据结构在之-最小堆的生成算法(下滑调整与上滑调整采用递归算法) 。

3、Huffman树实现源代码

3、1 HuffmanTree.h文件

#pragma once
#include"MinHeap.h"
//最小堆的应用之一：构建汉夫曼树

//哈夫曼树结点
template<class T>
struct HuffmanNode
{
	T m_tData;                //数据域  
	HuffmanNode<T>* m_ptLChild;  //指向左孩子的指针
	HuffmanNode<T>* m_ptRChild;  //指向右孩子的指针
	HuffmanNode<T>* m_ptParent;  //指向父节点的指针
	//默认构造函数
	HuffmanNode() :m_ptLChild(nullptr), m_ptRChild(nullptr), m_ptParent(nullptr) {}
	//构造函数
	HuffmanNode(const T& data, HuffmanNode<T>* lc = nullptr,
		HuffmanNode<T>* rc = nullptr, HuffmanNode<T>* p = nullptr) {
		m_tData = data;
		m_ptLChild = lc;
		m_ptRChild = rc;
		m_ptParent = p;
	}

	HuffmanNode(const HuffmanNode<T>& node) {
		this->m_tData = node.m_tData;
		this->m_ptParent = node.m_ptParent;
		this->m_ptLChild = node.m_ptLChild;
		this->m_ptRChild = node.m_ptRChild;
	}

	//判大小重载，在构建哈夫曼树的时候需要用到最小堆，最小堆的建立需要判断大小
	bool operator >(const HuffmanNode<T>& node) { return this->m_tData > node.m_tData; }
	bool operator <= (const HuffmanNode<T>& node) { return this->m_tData <= node.m_tData; }
};

template<class T>
class HuffmanTree
{
public:
	HuffmanTree(const T arr[], const int size);  //构造函数
	HuffmanTree() { m_ptRoot = nullptr; }        //默认构造函数
	~HuffmanTree() { DeleteTree(m_ptRoot); }     //析构函数
	void Display() { Display(m_ptRoot); }        //输出汉夫曼树
private:
	HuffmanNode<T>* m_ptRoot;                    //哈夫曼树的根节点
	void DeleteTree(HuffmanNode<T>* root);       //删除哈夫曼树
	//合并树
	void MergeTree(HuffmanNode<T>& lc, HuffmanNode<T>& rc, HuffmanNode<T>* &p);
	void Display(HuffmanNode<T>* root);        //输出汉夫曼树
};

//哈夫曼的函数构造函数
//利用权值为arr[0]-arr[size - 1]来构造二叉树
template<class T>
HuffmanTree<T>::HuffmanTree(const T arr[], const int size){
	//声明一个最小堆对象
	MinHeap<HuffmanNode<T>> minHeap;
	//依次为最小、次小、父节点
	HuffmanNode<T>*first, *second, *parent = nullptr;

	//先将数组装入最小堆中
	for (int i = 0; i < size; i++) {
		HuffmanNode<T>* tmp = new HuffmanNode<T>(arr[i]);
		minHeap.Insert(*tmp);
	}

	//进行size - 1次循环就可以构建哈夫曼树
	for (int i = 0; i < size - 1; i++) {
		first = new HuffmanNode<T>();  //一定要在堆中申请内存，临时变量是不行的
		second = new HuffmanNode<T>(); //临时变量的话在这个函数退出之后，只能找到顶点了

		minHeap.RemoveMin(*first);     //从最小堆中取出最小结点,从这里可以看书，要定义复制构造函数！！！！！
		minHeap.RemoveMin(*second);    //从最小堆中再取出次小的结点
		MergeTree(*first, *second, parent);
		minHeap.Insert(*parent);
	}
	m_ptRoot = parent;                //将根节点指向最终树的源点
}

//删除哈夫曼树
template<class T>
void HuffmanTree<T>::DeleteTree(HuffmanNode<T>* ptroot) {
	//递归删除
	if (ptroot != nullptr) {
		DeleteTree(ptroot->m_ptLChild);
		DeleteTree(ptroot->m_ptRChild);
		delete ptroot;
	}
}

//合并树
template<class T>
void  HuffmanTree<T>::MergeTree(HuffmanNode<T>& lc, HuffmanNode<T>& rc, HuffmanNode<T>* &parent) {
	parent = new HuffmanNode<T>();      //为父结点分配内存
	//parent新树左右指针指向参数中的左子树与右子树，值为两个子树的值之和
	parent->m_ptLChild = &lc;
	parent->m_ptRChild = &rc;
	parent->m_tData = lc.m_tData + rc.m_tData;
	//两个子树父节点指向参数中的parent新树
	lc.m_ptParent = parent;
	rc.m_ptParent = parent;
	
}

//输出汉夫曼树
template<class T>
void HuffmanTree<T>::Display(HuffmanNode<T>* root) {
	//前序遍历输出
	if (root != nullptr) {
		std::cout << root->m_tData << "\t";   //输出顶点值
		Display(root->m_ptLChild);       //递归调用，输出右孩子
		Display(root->m_ptRChild);       //递归调用，输出左孩子
	}
}

3、2 main.cpp文件

//#include"MinHeap.h"
#include"HuffmanTree.h"
#include<iostream>
using namespace std;

int main() {
	float arr[] = { 1.2, 3.5, 6.0, 2.2, 4.1, 20.4 };
	HuffmanTree<float> hf(arr, 6);
	hf.Display();
	return 0;
}

3、3 结果显示