最近笔者在学习的过程中接触了两种搜索算法，并为此困惑了非常久，就在这里分享下心得吧。
先大概讲下两个算法的思想：
DFS是遍历与递归的嵌套回溯算法，而BFS是遍历与队列的组合算法
说简单一点，DFS就是一条路走到黑，而BFS是每一层都走一遍再往下一楼走。
在学习过程中笔者深感单独看概念没有用，接下来笔者用几道比较经典的问题来讲一下；
深度优先搜索（BFS）
第一题是跳马（一道题可以讲深搜和广搜）（题目来源：洛谷）
# 马的遍历
## 题目描述
有一个 n *m 的棋盘，在某个点 (x, y)上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。
## 输入格式
输入只有一行四个整数，分别为 n, m, x, y。
## 输出格式
一个 n * m 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 -1）。
## 样例 #1
### 样例输入 #1
```
3 3 1 1
```
### 样例输出 #1
```
0 3 2
3 -1 1
2 1 4
```
## 提示
### 数据规模与约定
对于全部的测试点，保证 1 ≤ x ≤ n ≤ 400，1 ≤ y ≤ m ≤ 400
——————DFS题解———————————————————————————————————————
对于dfs搜索下的数据结构，这里用一张图来描述下
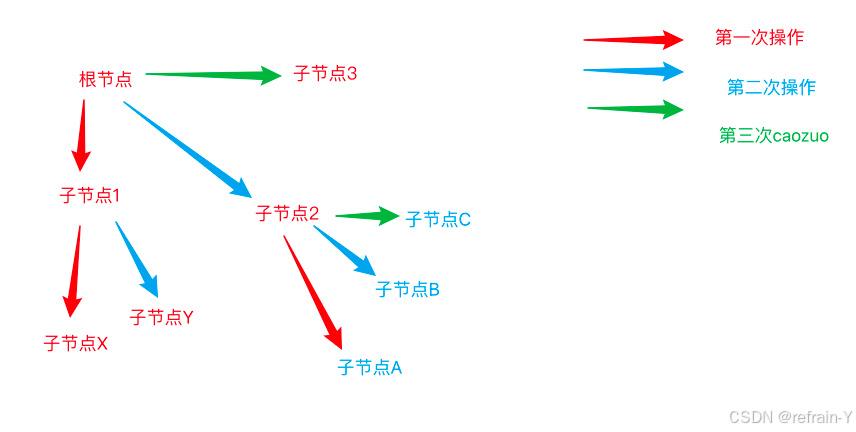
到达节点的底端则返回到上一个节点
文字描述为根-->子1-->子x-->子X-->子y-->子2-->子A-->子B-->子C-->子3；
从而对整个图（树）遍历
众所周知，根节点是子节点1的子节点，因为图的两个节点具有双向性，所以通过对根节点的标记可使双向性变成单向性，从而使图的搜索变为树结构。
大概知道DFS的运行结构了，那么我们可以开始着手写这道题了；
应该没有人没玩过象棋吧？马走日应该是人尽皆知的了，那么我们就看看在地图（棋盘）上应该怎么走吧：
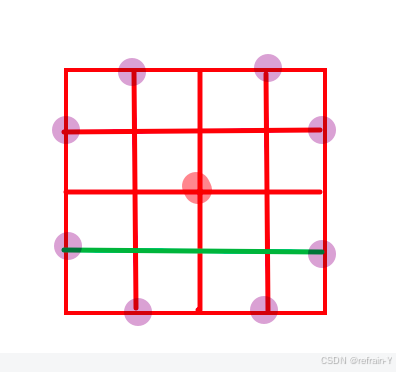马在红点可以走到所有的紫色点上。
所以我们可以用两个数组用于存放对应的移动的坐标的操作
int dx[8]={2,1, 2, 1,-2,-1,-1,-2};
int dy[8]={1,2,-1,-2,-1,-2, 2, 1};我们还需要创建两个一个二维数组用于记录步数与标记（在走过的地方势必不为0）
那我们就开始写dfs函数吧！
void dfs(int x,int y)
{
for(int i=0;i<=8;i++)
{
int a=x+dx[i],b=y+dy[i];//a与b为在移动后的坐标
if(a>=1 && b>=1 && a<=n &&b<=m && (cb[a][b]==0 || cb[a][b]>cb[x][y]+1))
{
//如果数组越界或者走过则不标记，除非走后的最新纪录步数更小
//if语句中判断（a，b）在界内且位置为空或者更新步数后更小
cb[a][b]= cb[x][y]+1;
dfs(a,b);//将该节点的子节点引入深搜
}
}
}完整代码如下
#include <iostream>
using namespace std;
int m=0,n=0,x=0,y=0,ans=0;
int dx[8]={ 1, 2,2,1,-1,-2,-2,-1};
int dy[8]={-2,-1,1,2, 2, 1,-1,-2};
int c[405][405]={-1};
void dfs(int x,int y)
{
for(int i=0;i<=8;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=1 && b>=1 && a<=n &&b<=m && (c[a][b]==0 || c[a][b]>c[x][y]+1))
{
c[a][b]= c[x][y]+1;
dfs(a,b);
}
}
}
int main()
{
cin>>n>>m>>x>>y;
c[x][y]=1;
dfs(x,y);
for(int l=0;l<=n;l++)
for(int r=0;r<=m;r++)
{
cout<<c[l][r]-1<<" ";
if(r==m)cout<<endl;
}
return 0;
}但是时间一定是会超过的，因为该走完第一个子节点的时候基本已经将所有位置标记过了，走完第二个子节点的时候又走遍了整个棋盘，数据一旦大了的话时间将非常长；
那就应该用BFS了
——————BFS题解——————————————————————————————————————
BFS 的结构在文章开头就说过了是每层走下去
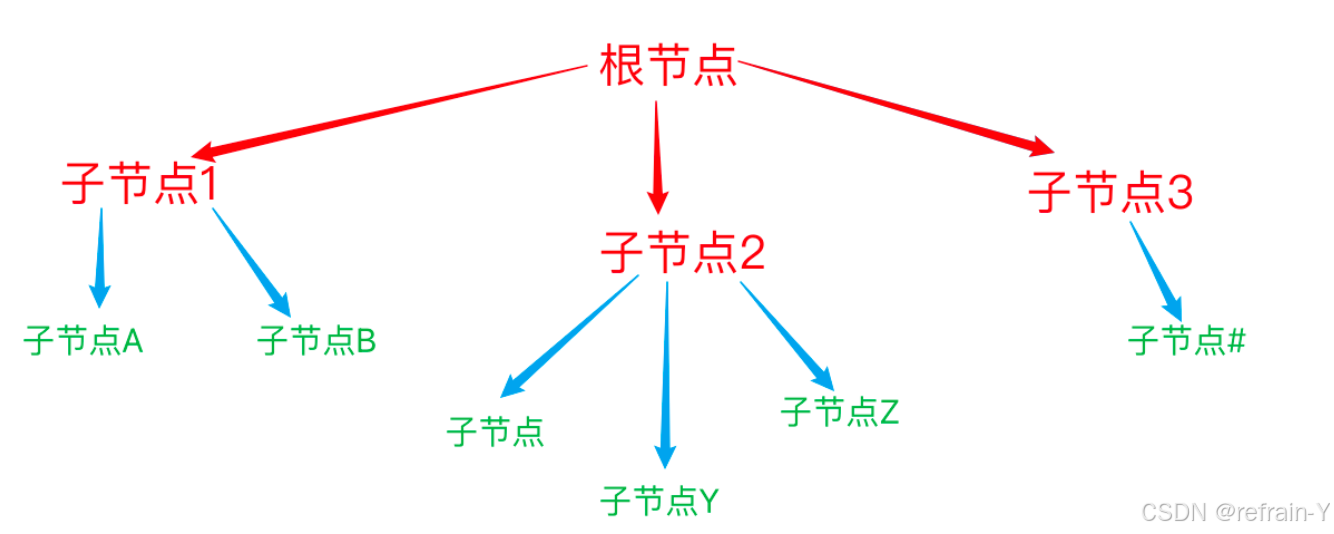
但是依然存在遍历的结构所以在子节点123间依然是存在一定的顺序结构的，这点需要注意，但是目前阶段貌似没有什么影响（
既然知道了BFS的结构的话那我们就需要考虑怎么去实现这个结构了。
我们可以用到STL容器库中的<queue>,在这里就简单介绍下几个需要用到的语句吧：
#include <queue>//此容器需要包含的文件
int x=0;
queue<int>q;//创建类型为int，名称为q的队列
q.push(x);//将变量x插入队尾
int y=q.front();//将队首的值赋给y，此时因为队列中只有x一个元素，所以此时y==x
q.pop();//将队首取出
q.size();//求队列长度
q.empty();//检测队列是否为空
详细内容可参考https://zh.cppreference.com/w/cpp/container/queue
棋盘是一个二维的空间，我们可以使用结构体或者make_pair来将两个坐标值变为一个变量
这里就不介绍结构体了，相信大家都对结构体有了解，只介绍make_pair的用法
queue<pair<int,int>>q;//创建两个值都为int类型的队列
q.push(make_pair(x,y));//将x,y成组放入队列
int a=q.front().first;//将组中的第一个元素(x)赋给a
int b=q.front().second;//将组中的第二个元素(y)赋给b有了这些知识基础我们就可以开始写bfs函数了，对于标记的思路与DFS函数中是通用的
void bfs(int x,int y)
{
q.push(make_pair(x,y));
c[x][y]=1;
while(q.size())//队列非空时则循环，直至队列为空
//也可写成while(!q.empty())
{
int kx=q.front().first;
int ky=q.front().second;
q.pop();//在取出队首的值后将其推出，防止卡循环
for(int i=0;i<8;i++)
{
int ix =kx + dx[i];
int iy =ky + dy[i];
if(ix>=1&&iy>=1&&ix<=n&&iy<=m&&!vis[ix][iy])
{
q.push(make_pair(ix,iy));//符合条件则将该点推入队列
c[ix][iy]=c[kx][ky]+1;
}
}
}
}将根节点推入后将根节点的值取出，将根节点推出并且将符合条件的子节点推入，在下一个循环里子节点将作为新的根节点。来看看完整的代码示例
#include <iostream>
#include <queue>
using namespace std;
int dx[8]={2,1, 2, 1,-2,-1,-1,-2};
int dy[8]={1,2,-1,-2,-1,-2, 2, 1};
int c[405][405]={0};
int vis[405][405]={0};
int n,m,x,y;
queue<pair<int,int>>q;
void bfs(int x,int y)
{
q.push(make_pair(x,y));
vis[x][y]=1;
c[x][y]=1;
while(q.size())
{
int kx=q.front().first;
int ky=q.front().second;
q.pop();
for(int i=0;i<8;i++)
{
int ix =kx + dx[i];
int iy =ky + dy[i];
if(ix>=1&&iy>=1&&ix<=n&&iy<=m&&!vis[ix][iy])
{
q.push(make_pair(ix,iy));
vis[ix][iy]=1;
c[ix][iy]=c[kx][ky]+1;
}
}
}
}
int main()
{
cin>>n>>m>>x>>y;
bfs(x,y);
for(int l=1;l<=n;l++)
for(int r=1;r<=m;r++)
{cout<<c[l][r]-1<<" ";if(r==m)cout<<endl;}
return 0;
}通过两个解题的方式可以理解DFS与BFS的大致思路，后续有空的话笔者还会写其他的题解
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
