【最短路】Bellmanford算法及链式前向星存图

既然学完动态规划了：01dp  多重dp
我们接着刷板子：最短路问题
最短路有很多种，这次我们先刷Bellmanford算法

先从图的存储方式说吧，以后每写一篇最短路就写一种存图的方式，这次是“链式前向星”
其实是一个很好理解的问题，因为一个节点指向其他节点的图长得就很像一个星星

话不多说，直接上我最开始学的代码，我认为可读性还是可以的

#include <iostream>
#include <vector>
using namespace std;
struct Edge{
    int next,goal,value;//上一个的位置，下一个节点，权值
};
vector<Edge>edge;
int cnt=0;
vector<int>head;
void addEdge(int u,int v,int w)//添加边，u起点，v终点，w边权
{
    edge[cnt].goal=v;
    edge[cnt].value=w;
    edge[cnt].next=head[u];//给定上一条边的编号（下标
    head[u]=cnt++;//更新编号，并且使cnt增加
}
int main()
{
    int n,m;cin>>n>>m;//n个节点，m条边
    edge.resize(m);
    head.assign(m,-1);//初始化，如果值为-1说明这是该节点的第一个输入的边
    int u,v,w;
    for(int i=0;i<m;i++)
    {
        cin>>u>>v>>w;
        addEdge(u,v,w);
    }
    for(int i=1;i<=n;i++)//遍历输出，优先以每个节点开始
    {
        cout<<i<<endl;
        for(int j=head[i];j!=-1;j=edge[j].next)
        {
            cout<<i<<" "<<edge[j].goal<<" "<<edge[j].value<<endl;
        }
        cout<<endl<<endl;
    }
    
    return 0;
}

这个代码可以读入一张n个节点m条边的图，并且按照出发点将边存储进图，你可以自己进行尝试

addEdge：链式前向星的重要实现部分，每次函数调用都会将数据存入结构体数组，并且将edge[i].next更新为上一个起始边为i的下标，应该是不难理解的，对吧(

如果看懂了，那我们开始简化这个代码，直接将addEdge函数放进main函数的读入中

ll next;
    for(int i=0;i<m;i++)
    {
        cin>>next>>edge[i].goal>>edge[i].value;
        edge[i].next=head[next];
        head[next]=i;
    }

对于存图的内容我们基本就理解到位了，接下来开始寻路的内容（敲黑板
 

寻路的部分非常简单，就是对每条边进行贪心比如说现在有如下数据

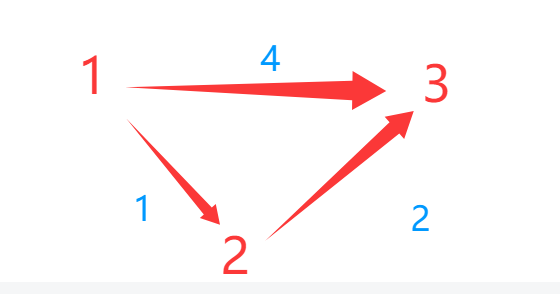
则我们可以进行一次贪心操作（也被称作松弛操作）

也就是的这条路比1-->3更短，所以我们直接记录1到3的最短路径为1-->2-->3，也就是长度由4变为3，于是我们新开一个数组，记录每个点到原点的距离，每次向外松弛一次，这个操作模式有点类似bfs

上代码

vector<ll>dist(n+1,INT_MAX);//记录原点到每个点距离，且初始到原点无限远
dist[1]=0;//起点到起点的距离为0
    for(ll x=1;x<=k;x++)//松弛至多k次，通常情况下k=n-1
    {   
        vector<ll> tempDist=dist;//为了不影响之前状态，防止出现错误，所以复制一份
        for(ll i=1;i<=n;i++)
        {
            if(dist[i]==INT_MAX)continue;//经过X条边不能到达则跳过不必要循环
            for(ll j=head[i];j!=-1;j=edge[j].next)
            tempDist[edge[j].goal]=min(tempDist[edge[j].goal],dist[i]+edge[j].value);
            //松弛操作
        }
        dist=tempDist;
    }
    if(dist[n]==INT_MAX)cout<<"impossible"<<endl;//不能经过k条路到达n
    else cout<<dist[n]<<endl;

每次松弛只向外松弛一层（多走过一条边），所以可以通过外层循环对于经过边的数量进行限制
内层循环就是链式前向星的遍历