【机器学习】浅谈聚类算法

K均值聚类（K-means）

---

---

简述

---

分类是根据样本某些属性或某类特征（可以融合多类特征），把样本类型归为已确定的某一类别中。机器学习中常见的分类算法有：SVM(支持向量机)、KNN(最邻近法)、Decision Tree(决策树分类法)、Naive Bayes(朴素贝叶斯分类)、Neural Networks(神经网络法)等

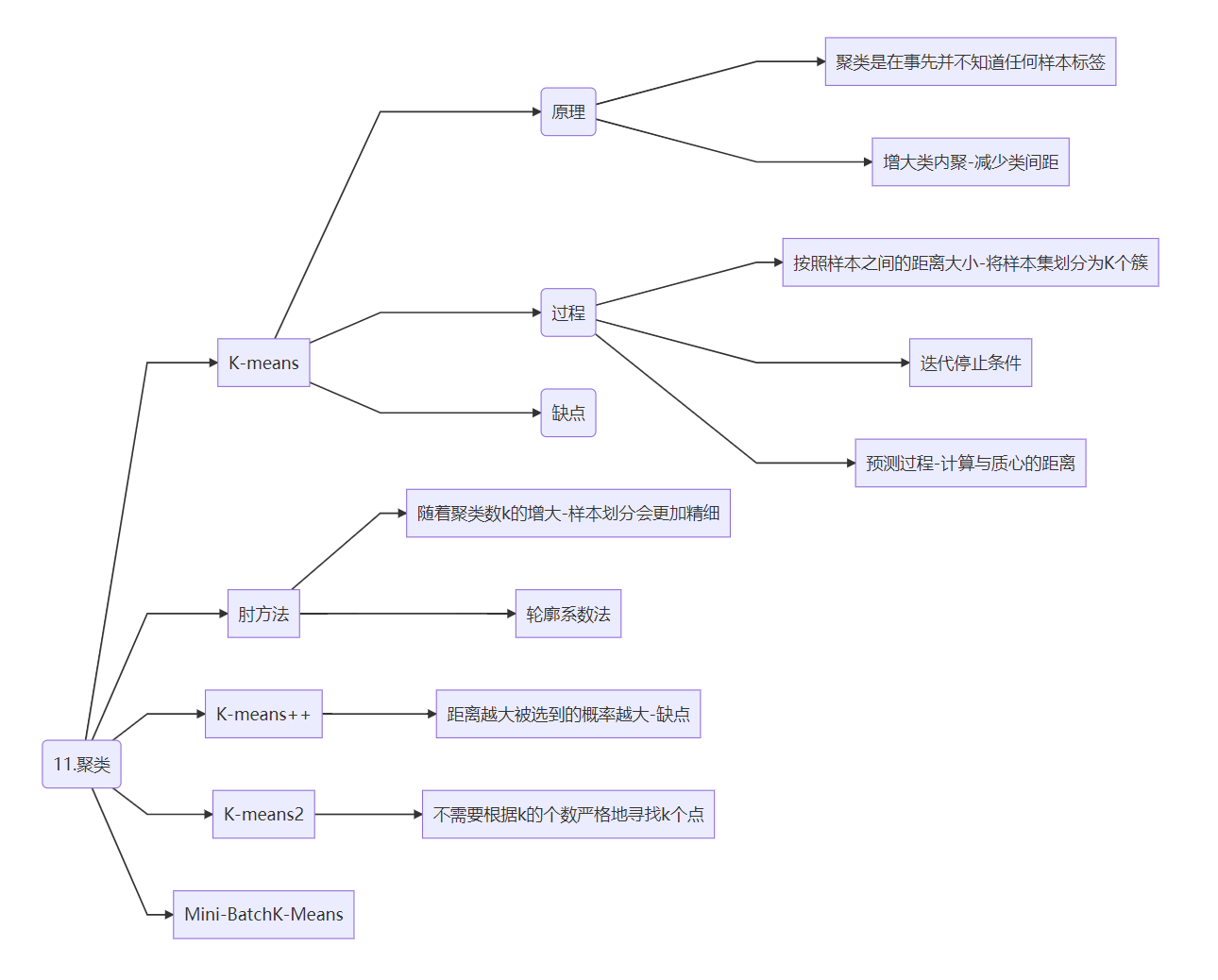
与分类、序列标注等任务不同，聚类是在事先并不知道任何样本标签的情况下，通过数据之间的内在关系把样本划分为若干类别，使得同类别样本之间的相似度高，不同类别之间的样本相似度低（即增大类内聚，减少类间距）

K-Means Clustering（K均值聚类），就是最典型的聚类算法之一。K-Means算法有大量的变体，包括初始化优化K-Means++以及大数据应用背景下的k-means||和Mini Batch K-Means

K-means聚类算法需要事先指定要分成的簇的数量。这是因为K-means算法是一种无监督学习算法，它在执行聚类时需要事先知道要分成的簇的数量。

在K-means算法中，我们需要指定一个参数K，它表示要分成的簇的数量。算法将尝试将数据点分配到K个簇中，以使得簇内的点相似度最大化，簇间的点相似度最小化。

因此，对于已知有多少分类的分类任务，可以使用K-means算法，并将簇的数量设置为已知的分类数。然后根据聚类结果来进行后续的分析或决策。

需要注意的是，K-means算法对于不同的初始化和数据分布可能会产生不同的聚类结果，因此在使用K-means算法时需要多次运行并选择最好的聚类结果。

K-means算法过程

---

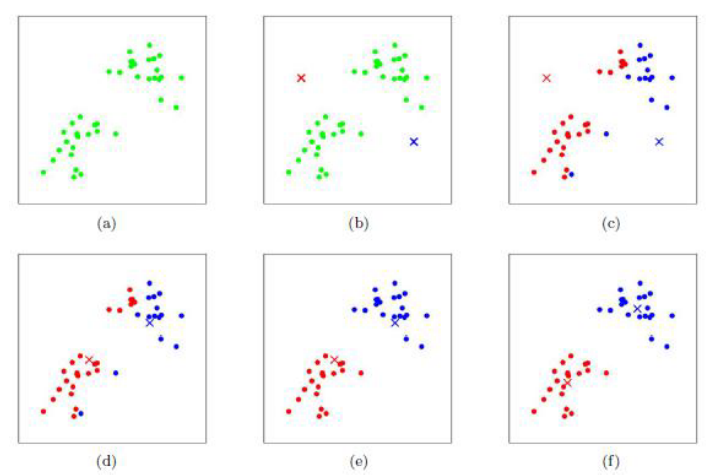
K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大，K-Means的迭代求解过程

停止更新条件: 质心向量不再变化或者规定迭代次数

迭代过程：

**预测过程：**计算与质心的距离

K-means算法缺点

---

缺点一：聚类中心的个数K需要事先给定，但在实际中K值的选定是非常困难的，很多时候我们并不知道给定的数据集应该聚成多少个类别才最合适
缺点二：k-means算法需要随机地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果，有可能导致算法收敛很慢甚至出现聚类出错的情况

针对第一个缺点：很难在k-means算法以及其改进算法中解决，一般来说，我们会根据对数据的先验经验选择一个合适的k值，如果没有什么先验知识，则可以通过“肘方法”选择一个合适的k值
针对第二个缺点：可以通过**k-means++**算法来解决

import numpy as np
from sklearn.cluster import KMeans

X = np.array([[1, 2], [2, 2], [6, 8], [7, 8]])
# C = np.array([[1, 2], [2, 2]])

kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
print(kmeans.cluster_centers_)  ##簇中心
print(kmeans.labels_)  ###簇的标签
print(kmeans.score