内容概览：信息熵、决策树、决策树优化、剪枝、决策树可视化
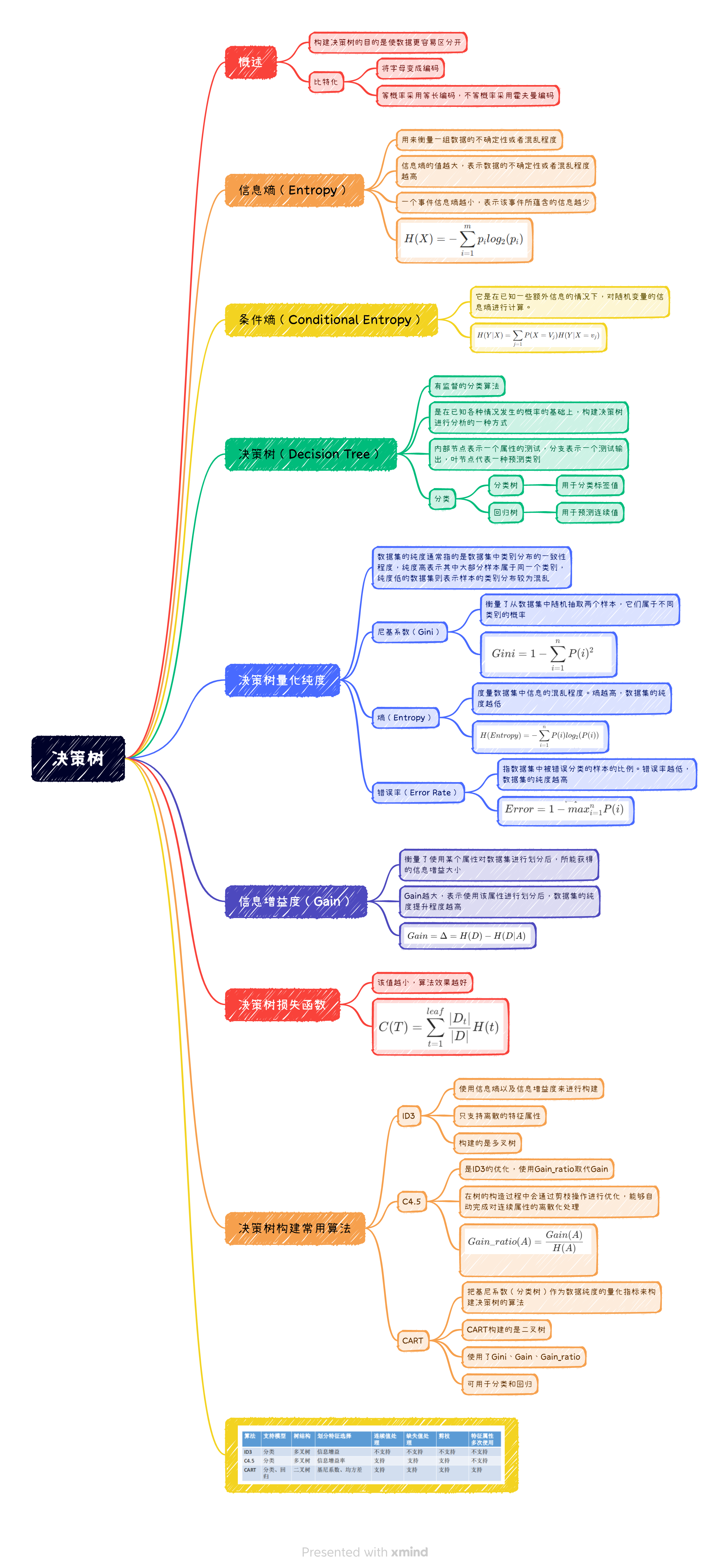
决策树概述
构建决策树的目的是使数据更容易区分开
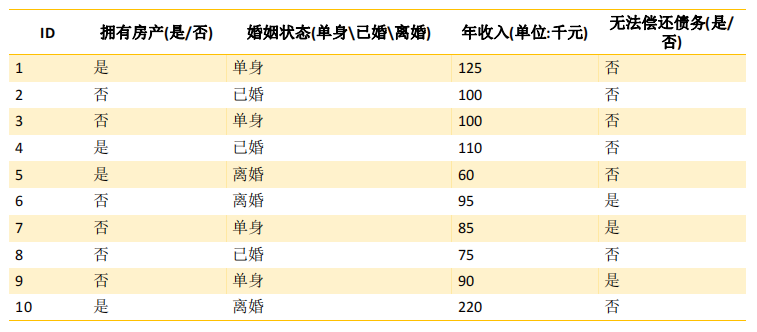
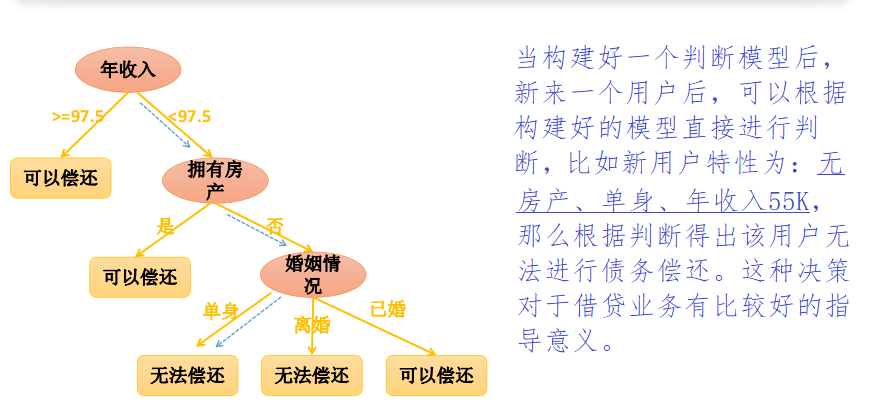
基础概念
比特化(Bits)
- 假设存在一组随机变量X，各个值出现的概率关系如图；
- 现在有一组由X变量组成的序列：BACADDCBAC…; 如果现在希望将这个序列转换为二进制进行网络传输，那么我们得到一个这要的序列；01001000111110010010…
P(X=A)=1/4P(X=B)=1/4P(X=C)=1/4P(X=D)=1/4P(X=A)=1/4\quad\quad P(X=B)=1/4 \\ P(X=C)=1/4\quad\quad P(X=D)=1/4P(X=A)=1/4P(X=B)=1/4P(X=C)=1/4P(X=D)=1/4
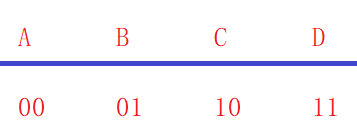
- 而当X变量出现的概率值不一样的时候，对于一组序列信息来讲，每个变量平均需要多少个比特位来描述呢？？
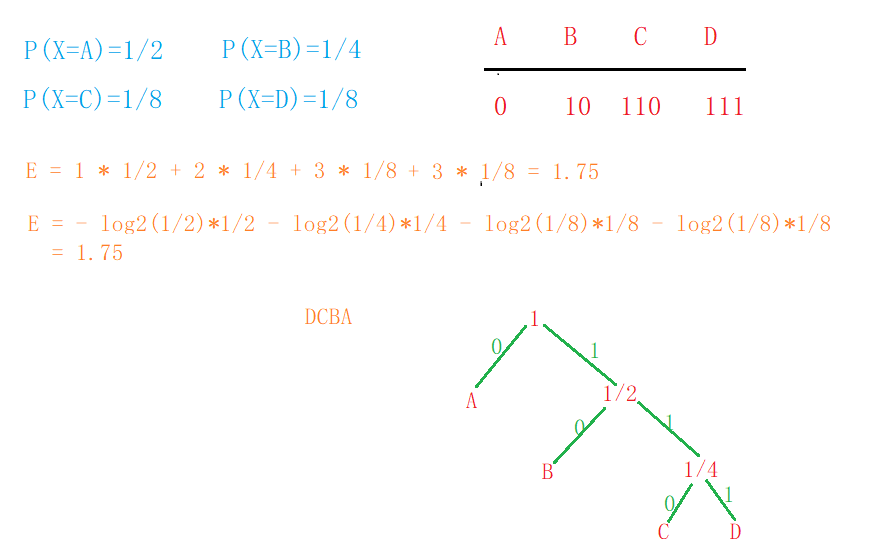
一般化的比特流（Bits）
- 假设现在随机变量X具有m个值，分别为: V1 ,V2 ,…,Vm；并且各个值出现的概率如下表所示；那么对于一组序列信息来讲，每个变量平均需要多少个比特位来描述呢??
P(X=V1)=p1P(X=V2)=p2...P(X=V1)=p1 \quad P(X=V2)=p2 ...P(X=V1)=p1P(X=V2)=p2...
- 可以使用这些变量的期望来表示每个变量需要多少个比特位来描述信息：E(X)=−p1log2(p1)−p2log2(p2)−...−pmlog2(pm)=−∑i=1mpilog2(pi)E(X)=-p_{1}log_{2}(p_{1})-p2log_{2}(p_{2})-...-p_{m}log_{2}(p_{m}) \\ =-\sum_{i=1}^{m}p_{i}log_{2}(p_{i})\quad\quad\quad\quad\quad\quad\quad\quad\quadE(X)=−p1log2(p1)−p2log2(p2)−...−pm</
最低0.47元/天 解锁文章
扫一扫
799
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
