吴恩达《Machine Learning》-Linear Regression with Multiple Variables多元线性回归（四）

多特征情况Multiple Features

多特征角标解释：

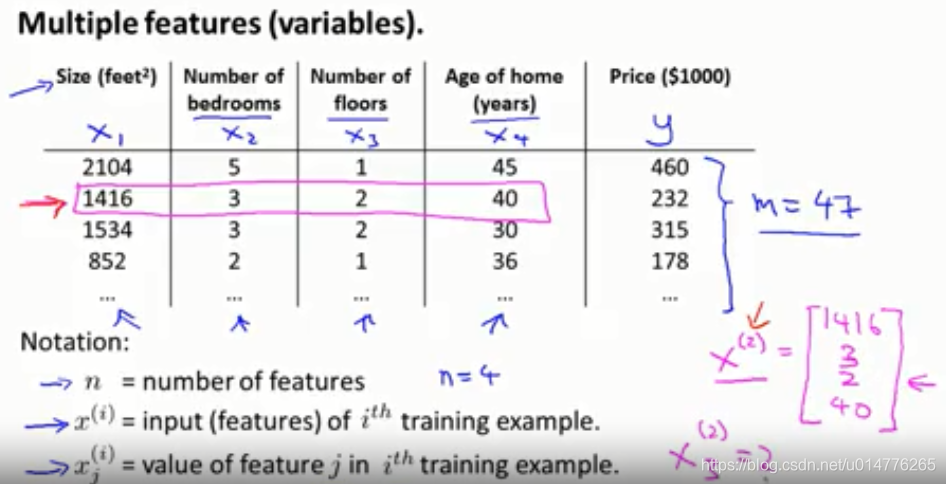
m 样本个数
n 特征个数 本例中，n=4 （x1，x2，x3，x4）
x(i)第i行特征向量 x(2)=[1416，3，2，40]
xj(i) 第i行特征向量的第j个特征值 x3(2)=2

练习题：

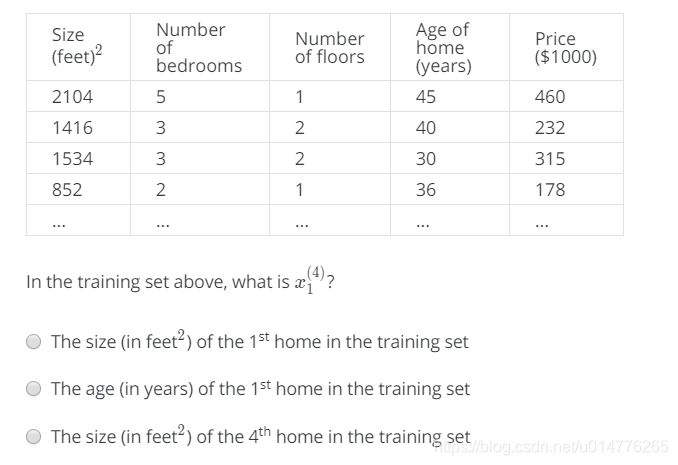
选择（C）第4行第一个。（o(╥﹏╥)o 英文看了一会才看懂）

多元线性回归multivariate linear regression

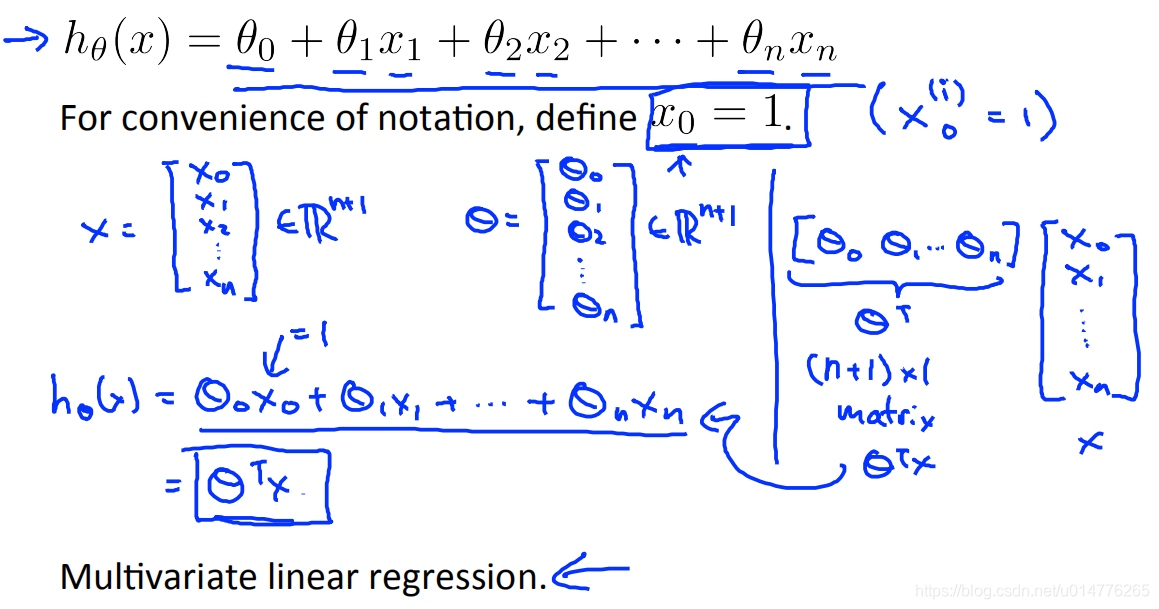
特征向量 x=[x0,x1,x2…xn]
参数向量 θ = [θ0,θ1,θ2…θn]
定义x0=1 本例中θ0x0=θ01=θ0

解释：为何增添x0=1

为了矩阵运算的方便。如此，参数向量矩阵 θ = [θ0,θ1,θ2…θn] 为一行n+1列，特征向量矩阵 x=[x0,x1,x2…xn] 为n+1行1列。只有行列相同都为n+1的两个矩阵才可以相乘，进行矩阵运算。

英文解释：

意思是：

1 by （n+1） ：一行 n+1列的矩阵

多变量梯度下降 Gradient Descent for Multiple Variables

使用向量J(θ)来代替J( θ0,θ1,θ2…θn)
损失函数变成：

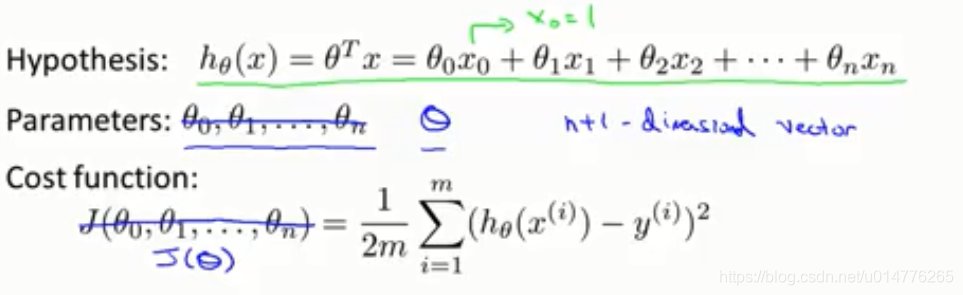
梯度下降算法变成：

练习题：

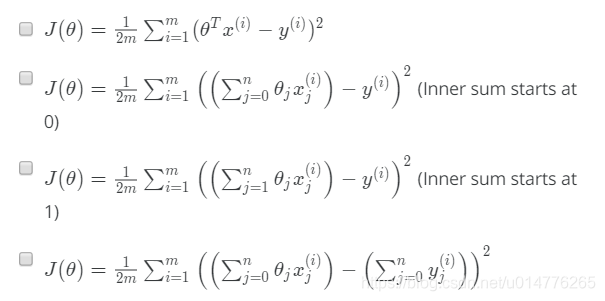
选择（A,B）本题比较重要建议多看
A选项.x(i)代表i行向量 故乘以θ向量的转置
B选项.xj(i)代表i行向量，第j个值，故乘以θ向量中第j个

单一特征梯度下降与多特征梯度下降对比：

单一特征时（因为特征向量只有一行）：x(i)表示 第一行 第i个值
多特征时：xj(i)表示第i行第j个值。故多特征 x0(i)= 单特征 x(i)

特征缩放 Feature Scaling （标准化）

不需要很精准，目的为了梯度下降更快收敛
如下图，x1的取值为0-2000，而x2的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快。
故采用特征缩放，来使特征都在统一范围内。

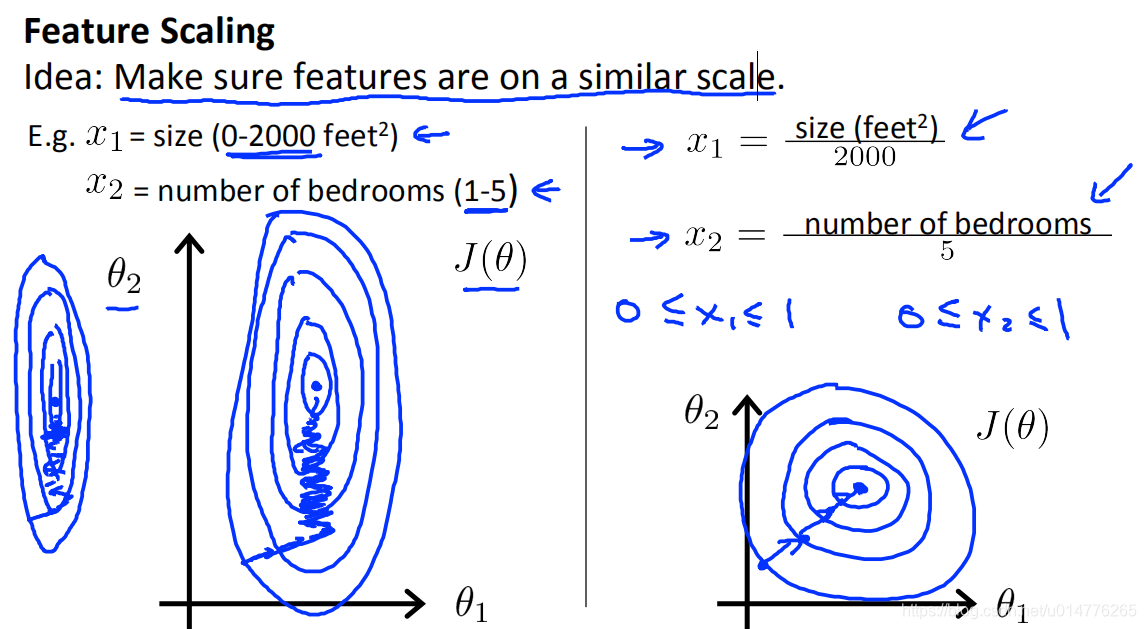
缩放范围：
区间[-1,1]比较好。具体举例如下图：

均值归一化 Mean normalization （归一化）

均值归一化从输入变量的值中减去输入变量的平均值，从而使输入变量的新平均值为零。

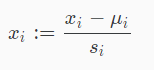
将特征归一到区间[-0.5,0.5]

注意

x0特征 不需要归一化

一般方法：

x1=x1-均值/数值范围(最大值-最小值) 或者 平方差

练习题：

选择(D) 为归一化.

判断梯度下降算法是否正确工作

在梯度下降中，损失函数J(θ)应该在每一轮的迭代中 越来越小。

方法一 看图：

图中可以看到300-400曲线 J(θ)几乎平，不再大幅下降，接近收敛

方法二 收敛测试：

每一轮中的J(θ)下降少于门限值(10^-3)。门限值需要人为定义且需要经验

常见错误案例：

解决方案：使用小一点的学习率α

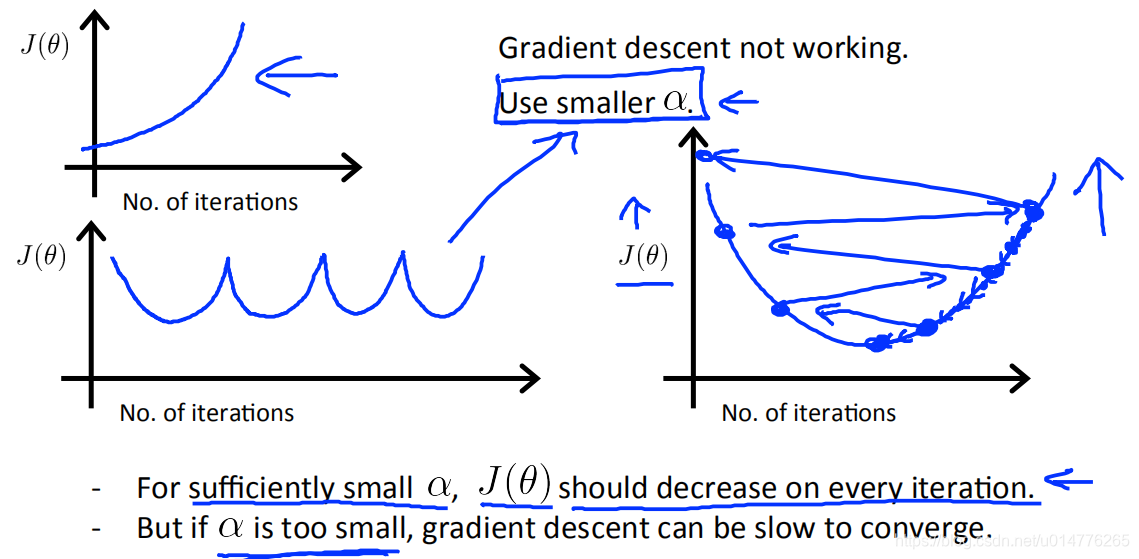
练习题：

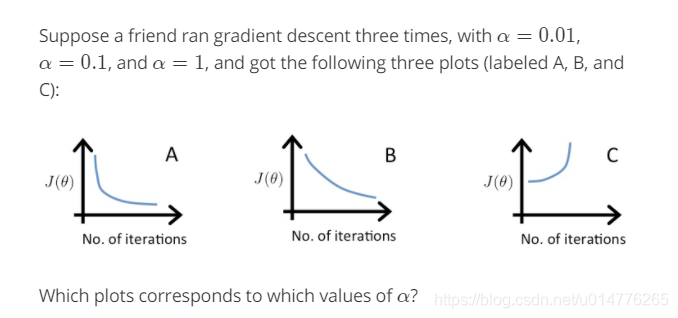
选择(B)
在图C中，成本函数在增加，因此学习率设置得太高。图A和图B都收敛到成本函数的最优值，但图B收敛得很慢，所以它的学习率设置得太低。图A位于两者之间。

选择学习率α：

定义新特征

房屋长*房屋宽=房屋面积

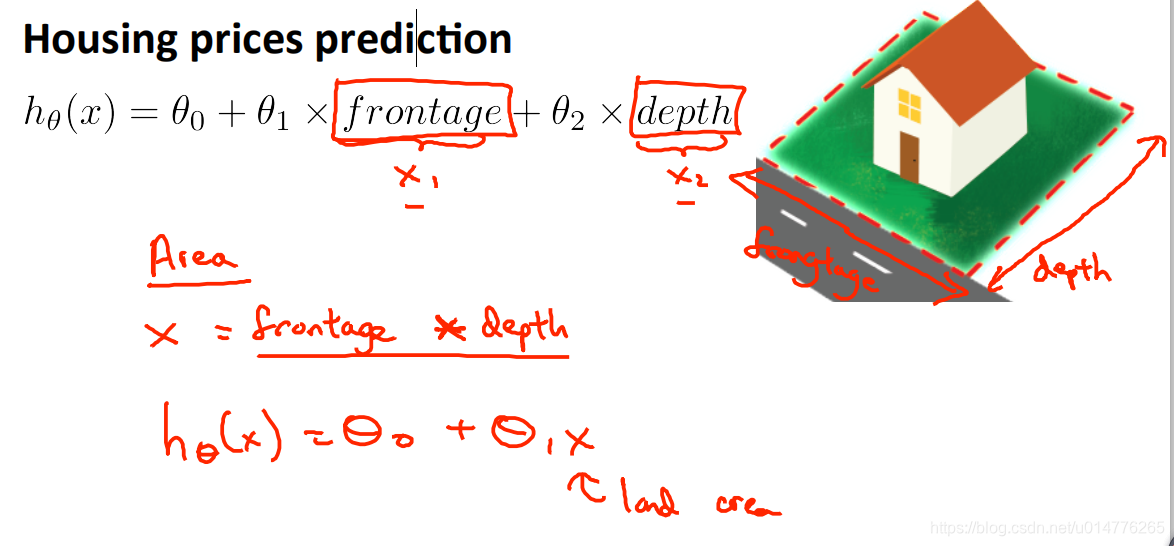
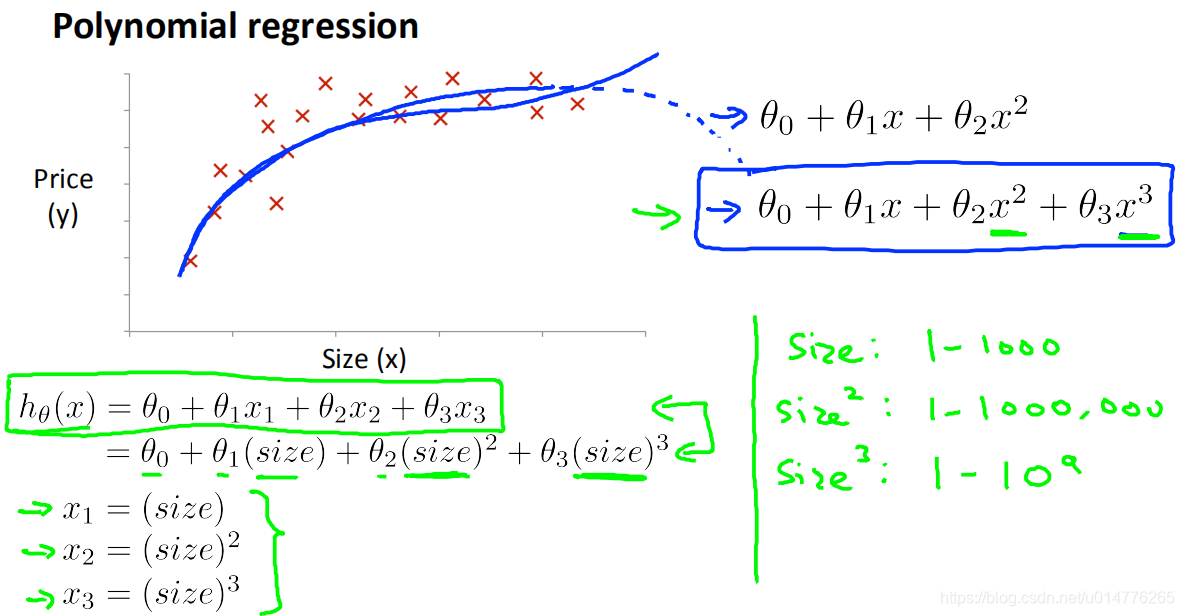
特征选择 polynomial regression 多项式回归

假设函数不适合数据，不是线性的（直线）。
我们可以假设函数成为二次、三次或平方根函数（或任何其他形式）来改变它的行为或曲线。

要记住的一件重要的事情是，如果以这种方式选择特性，那么特性缩放就变得非常重要。

使用特征的次方来代替特征

在多项式回归 标准化，归一化很重要，
因为size：1-1000
size^：1-1000000
size^3：1-109

练习题：

选择（C）。
解释：x1范围在1-1000，x2范围在0-32.故两个都应该在同样大小范围。

正态方程 normal equation

用来求解θ值，寻找最佳的θ值

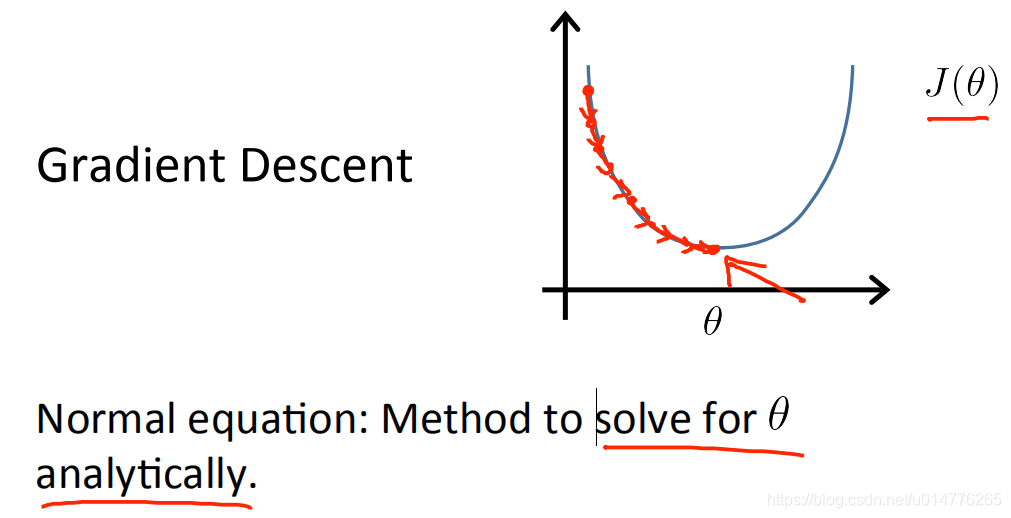
导数为0的地方，是二次函数的最低点。即为最优的θ值。
故，多维J( θ0,θ1,θ2…θn)损失函数 方法为，求θ0,θ1,θ2…θn的偏导，并使偏导数为0

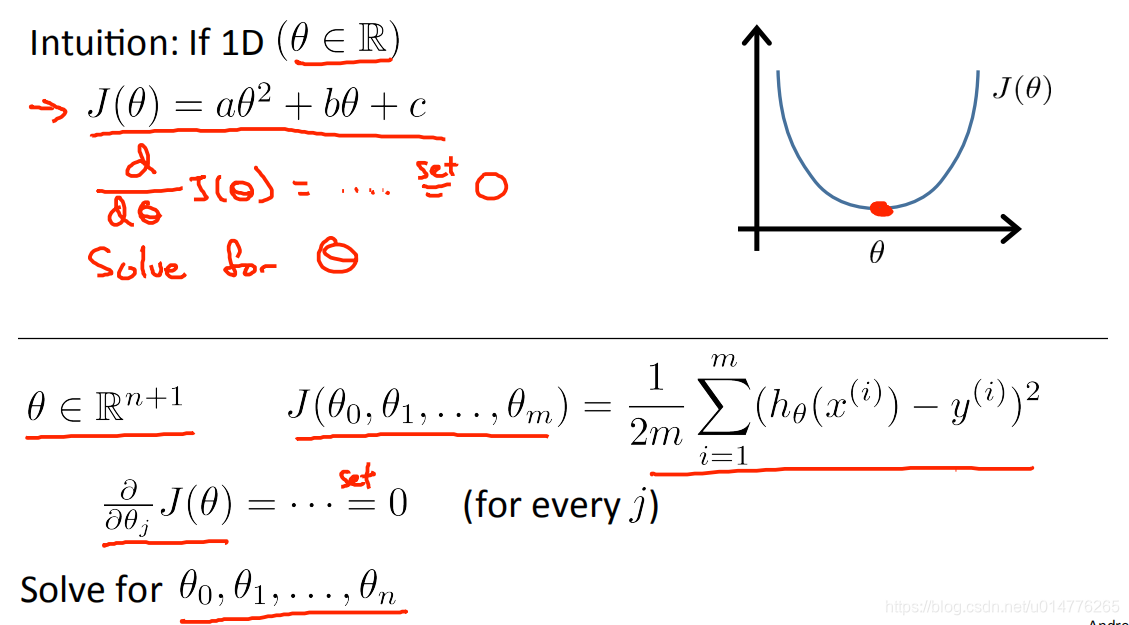
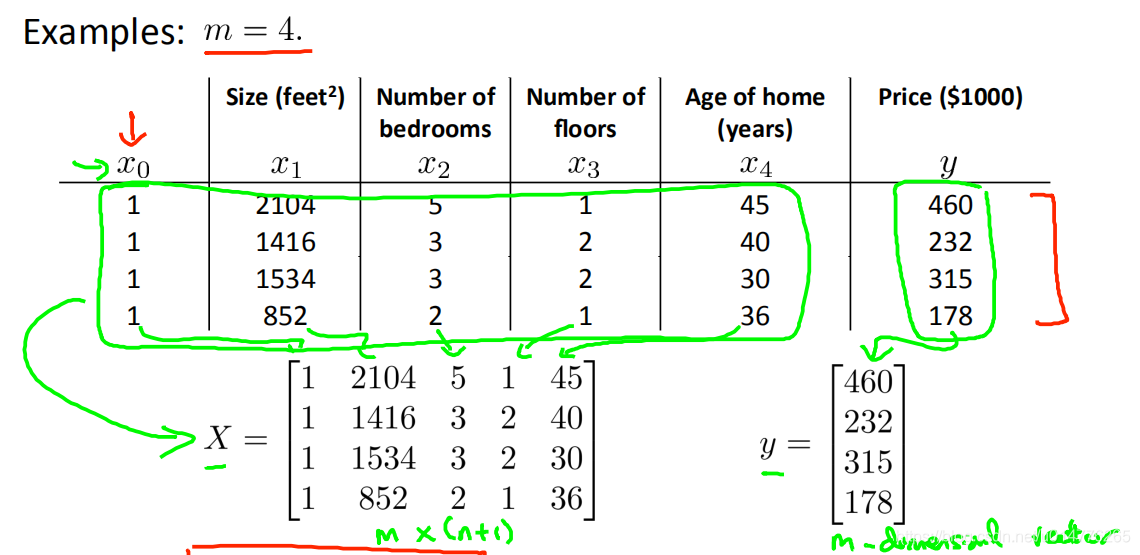
设计矩阵design matrix

将所有特征变成m行n+1列矩阵X，所有结果变成m行的向量Y

最优θ值，可以用矩阵求解出来

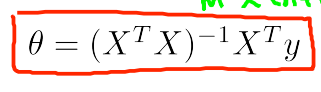
当x(i)为列向量时，上面的公式 X矩阵 ，为x(i)列项列的转置

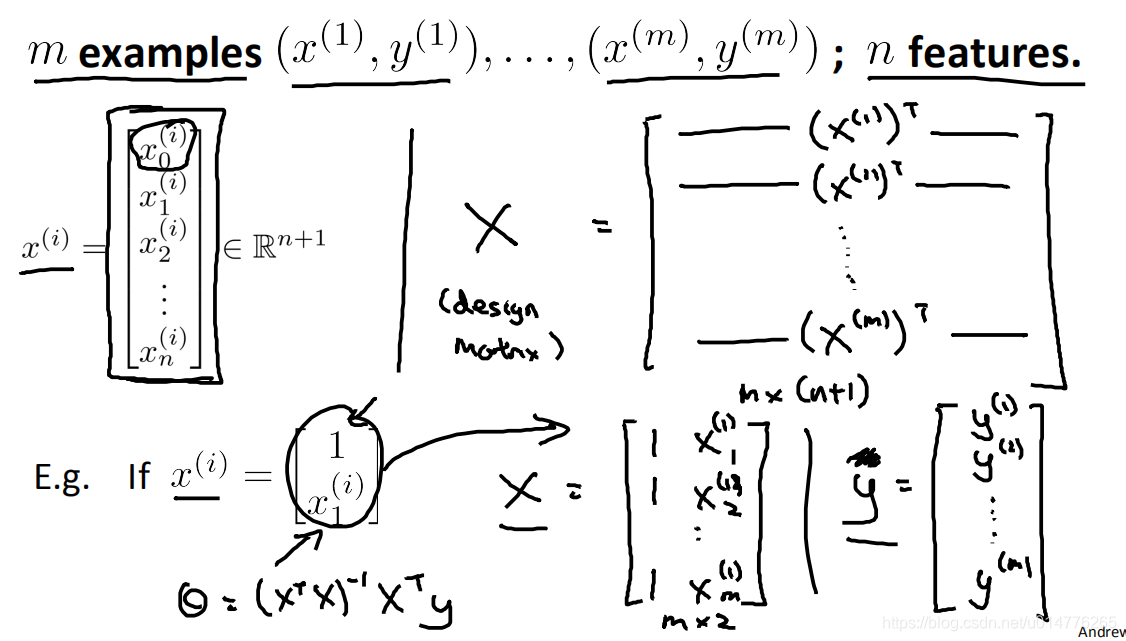
练习题：

选择(D)

Normal equation 正规方程组

正规方程组算法，对特征标准化不要求。

正规方程组 与 梯度下降 优缺点比较：

正规方程优点：

1.梯度下降法 需要手动选择 学习率α，正规方程法 不需要选择学习率α
2.梯度下降需要多轮迭代计算，细节计算较慢。正规方程法不需要多轮迭代计算

梯度下降优点：

1.梯度下降计算θ0，θ1…θn,当特征数量n很大的时候，运行速度依然很稳定。正规方程法计算θ向量，由于需要计算设计矩阵的逆矩阵，在特征数n很大时，时间复杂度很高，为o（n^3）
2.一般来说，特征数量n>10000时，采用梯度下降方法。

X^T*X不可逆的情况

1.两个特征在不相同的尺度，（即两个特征线性相关时）删除线性相关的另一个特征

如 x1尺度为平方英尺
x2尺度为平方米

2.有特别多特征时。

删除一些特征或者使用正规化方法
pseudo inverse function

当在octave使用正规方程组时，尽量使用pinv函数，而不是inv函数。当X^T*X不可逆的时候，pinv函数也可以给出对应的θ值。

练习题

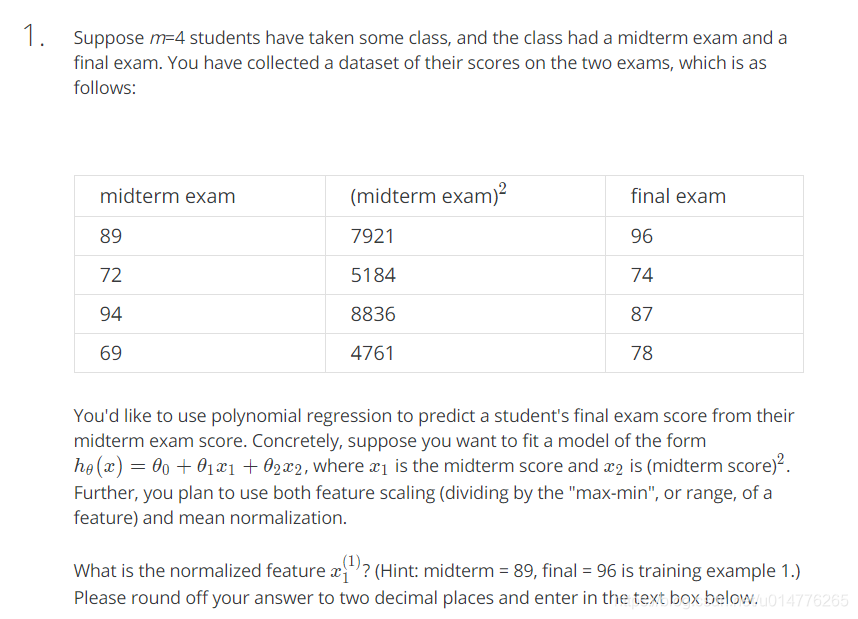
归一化处理：有两种方式：

1.（当前值-平均值）/（最大值-最小值）；

2.（当前值-平均值）/方差；

range=94-69=25
平均值：(89+72+94+69)/4=81
both feature scaling and mean normalization = (89-81)/25=0.32

（C）J(θ)下降很慢，且多轮迭代仍然下降。说明还未收敛。故需要将学习率α调大

（A）X是n+1列，因为在normal equation中，0号特征为1

（C）可以看到特征数并不是很大。故选择normal equation。特征数量n>10000时，采用梯度下降方法。

（C） 加快了梯度下降，通过更少的迭代来达到一个好的结果