吴恩达《Machine Learning》-gradient descent 梯度下降（三）

在实际中，我们有n个参数θ0，θ1，θ2```````θn
在此我们以两个参数举例，最小化J(θ0,θ1)

算法：

我们以θ0=0,θ1=0开始，
保持θ0，θ1参数改变，然后查看J(θ0,θ1)。
当J(θ0,θ1)为最小的时候 即为结束

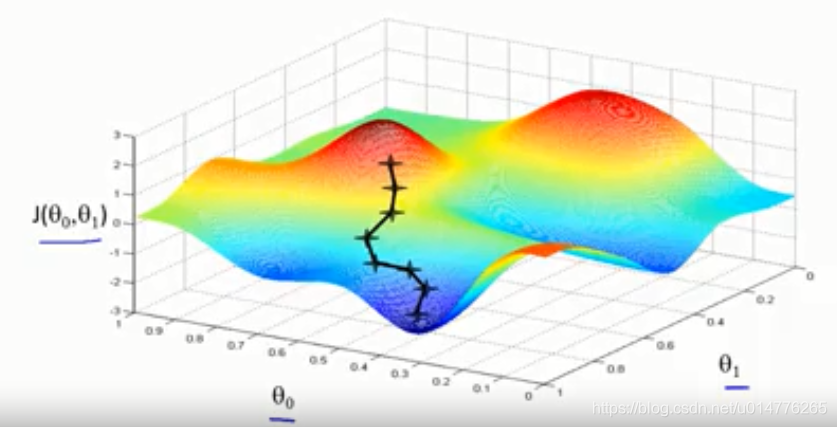
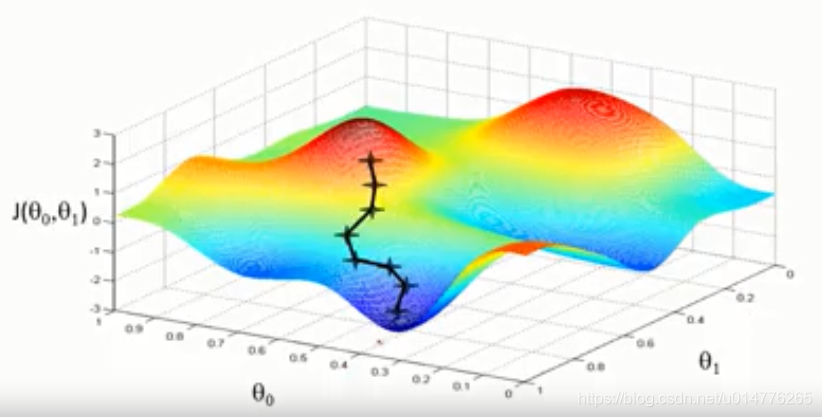
从图中点出发，假设你身处在山顶上，即为寻找当前最快下降的方向下山。
下降一个位置后，再次寻找当前最快下降的方向下山。
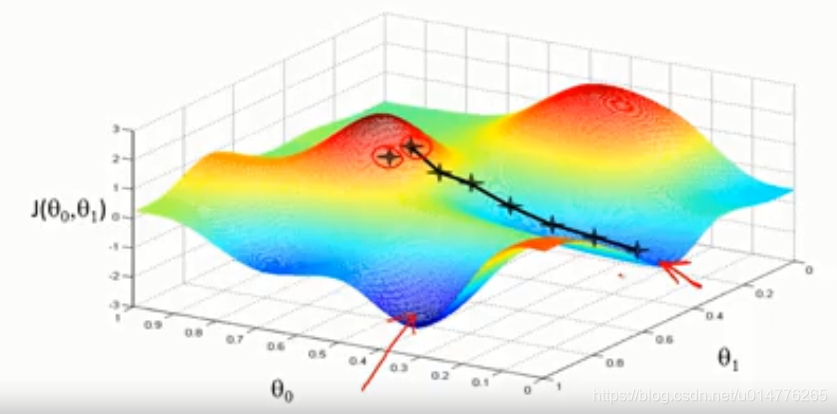
最后抵达了局部最优点(低点)

另一个位置，来到了其他的局部最优点(低点)


a：=b（：=为赋值）
a=b（为判断是否相等）
α为学习率 表明下降步子的大小。学习率越大，表明下降的步子越大。

注意：

θ0，θ1需要同时更新。
错误的方法为：
更新完θ0后，使用更新后的θ0的值，去计算θ1的值

检测题：

答案为(B)。注意同时更新的含义。

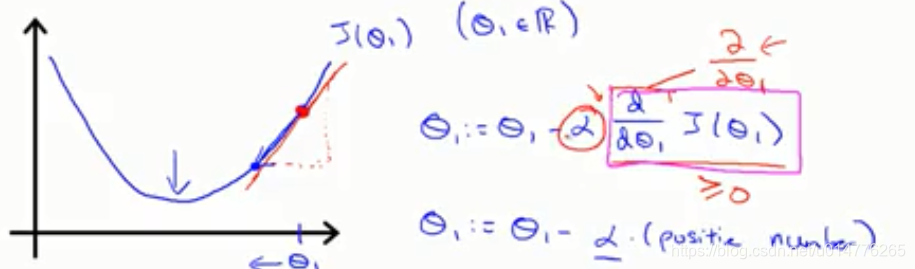
导数项∂J(θ1)/∂θ1解释：(以一个参数θ1举例)：

当导数为正数时,∂J(θ1)/∂θ1>=0，学习率α正数∂J(θ1)/∂θ1=正数
故θ1-α∂J(θ1)/∂θ1<0 所以θ1随着梯度越来越小

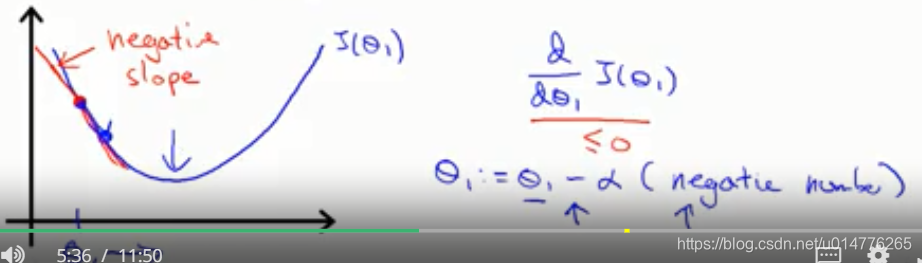
当导数为负数时,∂J(θ1)/∂θ1<=0，学习率α正数∂J(θ1)/∂θ1=负数
故θ1-α∂J(θ1)/∂θ1>0 所以θ1随着梯度越来越大

学习率α解释：

α小的话，相当于每次都迈出很小的一步。所以梯度下降将会变得很慢。但是不会跨过最优点，导致无法收敛。

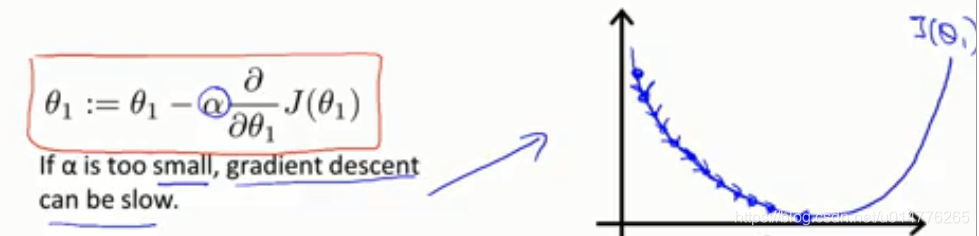
α大的话，相当于每次都迈出很大一步。所以梯度下降将会变得很快。但可能扩过最优点，导致无法收敛。（导数为负，梯度下降后的值，更大了）

练习题：

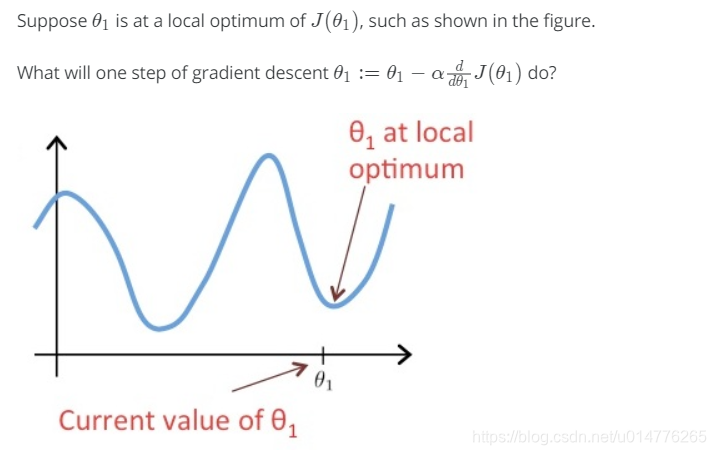
选择（A），导数为0，θ1=θ1 - 0 =θ1 故，保持不变

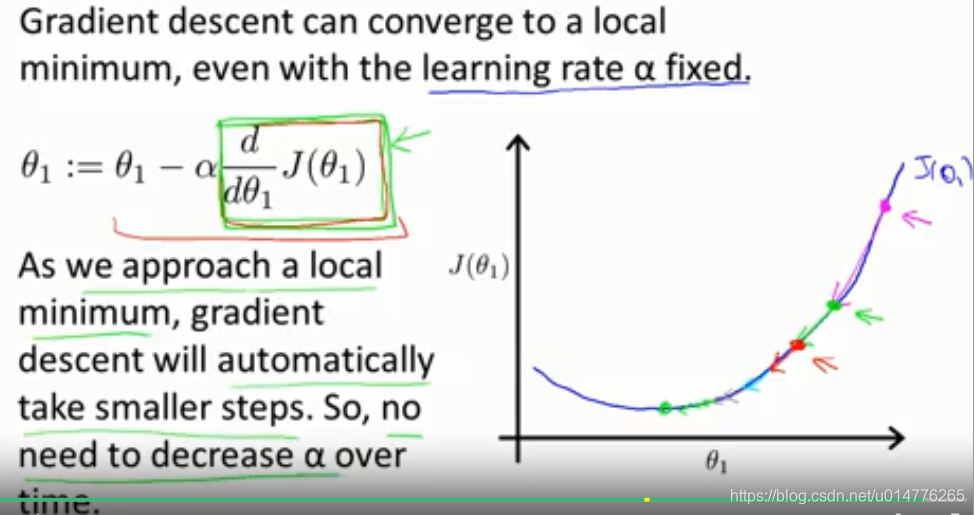
当梯度越来越小的时候，即为越来越接近0的时候。梯度下降算法，会越来越减小下降的步伐，来接近局部最优点。不需要每次减少学习率α。

梯度下降与线性回归相结合：

关键在于∂J(θ0，θ1)/∂θj的微分项

对∂θj求导：（此处推导较难，建议多看几遍）

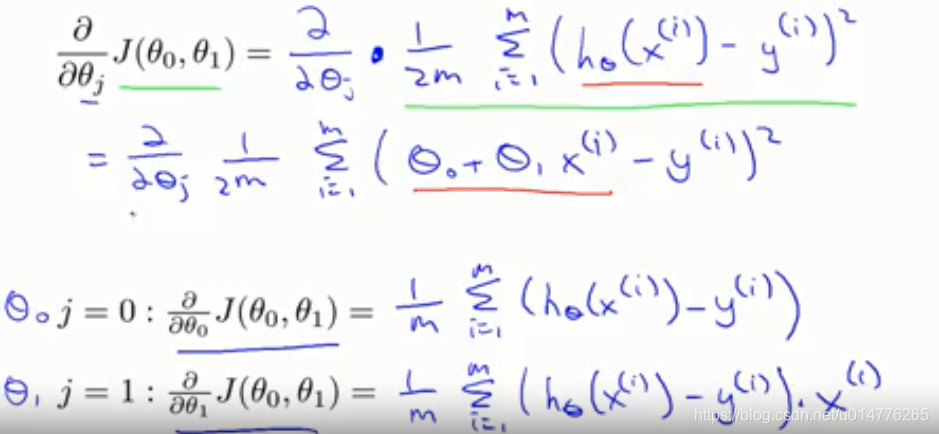
展开式 与结果：

梯度下降会产生很多局部最优值：

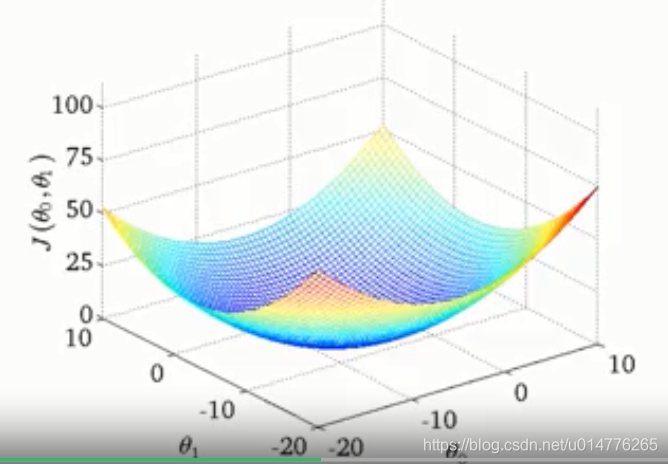
加入线性回归的损失函数后，线性回归的损失函数只有一个全局最优值（凸函数）：

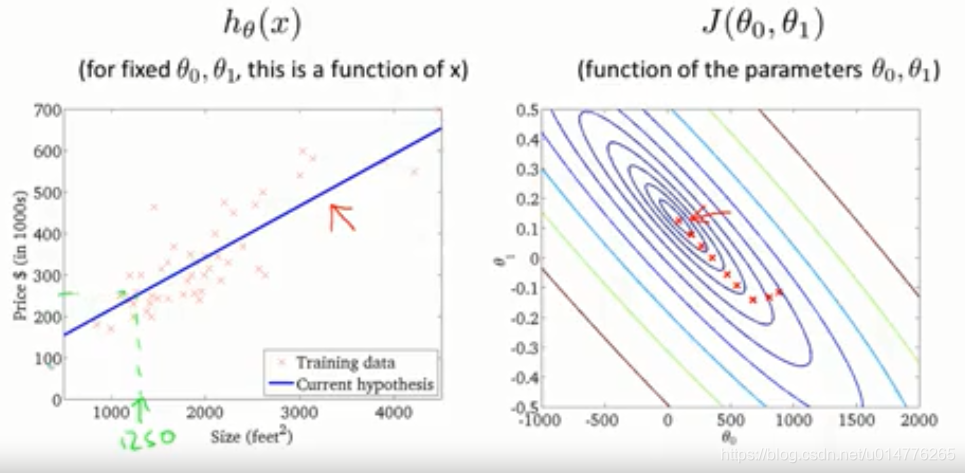
结果演示：

批处理梯度下降Batch Gradient Descent：

每次总是使用全部的样本来进行训练。因为∑（h（x(i)）-y(i)）

练习题

Which of the following are true statements? Select all that apply.(C，D)

A. To make gradient descent converge, we must slowly decrease α over time.

B. Gradient descent is guaranteed to find the global minimum for any function J(θ0​,θ1​).

C. Gradient descent can converge even if α is kept fixed. (But α cannot be too large, or else it may fail to converge.)

D. For the specific choice of cost function J(θ0​,θ1​) used in linear regression, there are no local optima (other than the global optimum).

解析：

C选项 当学习率持续改变的时候，梯度下降仍然能够收敛。但是过大的学习率会导致跨过最优点。
D选项 线性回归的损失函数只有一个全局最优点。所以使用梯度下降算法，只能找到一个全局最优点。