针对传递函数 G(s) = 1/[(Ts+1)s²] 的ADRC深度设计指南

一、对象特性分析与ADRC设计思路

该传递函数表示一个带惯性环节的二阶积分系统：

其核心特性：

1. 低频特性：双积分特性（1/s²），需要速度+位置跟踪

2. 高频特性：一阶惯性环节（1/(Ts+1)），带宽为 1/T rad/s

3. 相对阶：3阶系统（分母3阶，分子0阶）

ADRC设计策略：

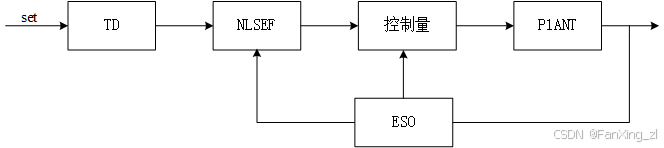
二、三阶ADRC控制器设计（推荐方案）

1. 系统方程重构

将原系统改写为：

定义扩张状态：

• x₁ = y（位置）
• x₂ = ẏ（速度）
• x₃ = ÿ（加速度）
• x₄ = f = -ÿ/T（总扰动和）

则状态方程为：

2. 四阶扩张状态观测器（ESO）设计