Linked List Cycle II（LeetCode）

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Note: Do not modify the linked list.

Follow up:
Can you solve it without using extra space?

判断链表知否存在环，存在的话返回换的初始结点。

思路：是否存在环，用快慢指针，如果最终慢指针追上了快指针，那么存在环，但是慢指针跟快指针相遇并不一定是在环的起点，关于环的初始结点位置存在以下分析：

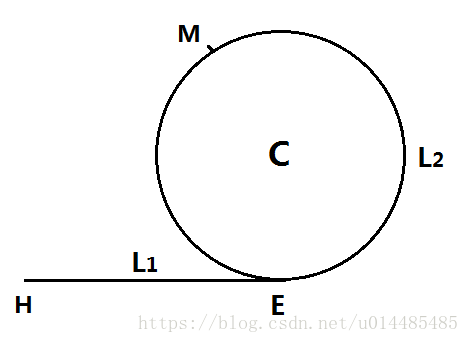
慢指针行进的距离为L1 + L2

快指针行进的距离为L1 + L2 + n * C

由于快慢指针行进的距离有2倍关系，因此：

2 * (L1+L2) = L1 + L2 + n * C => L1 + L2 = n * C => L1 = (n - 1)* C + (C - L2)

可以推出H到E的距离 = 从M出发绕环到达E时的路程

这样的话，我们只要让慢指针从头开始走，再次与快指针相遇就可以了。

struct ListNode {
	int val;
	ListNode *next;
	ListNode(int x) : val(x), next(NULL) {}
};
class Solution {
public:
	ListNode *detectCycle(ListNode *head) {
		if (head == NULL || head->next == NULL) {
			return NULL;
		}
		ListNode *fast = head;
		ListNode *slow = head;

		while (fast->next != NULL && fast->next->next != NULL)
		{
			fast = fast->next->next;//跳两个
			slow = slow->next;//跳一个
			if (slow == fast)
			{
				break;
			}
		}
		if (fast->next == NULL || fast->next->next == NULL)
		{
			return NULL;
		}
		slow = head;
		while (slow!=fast)
		{
			slow = slow->next;
			fast = fast->next;
		}
		return slow;
	}
};