从扩展黎曼泽塔函数构造物质和时空的结构-16

有了某个函数的导数这个概念，处理自然数全加和的问题就简单多了，

按照先前的正切算法，如果 是某个函数的导数，那么这个函数显然就是

原函数，

要求其自变量，

但是对于自然数范围内的质数来说， 显然是不成立的，但是不妨碍在周期回环的前提下成立。一个负数指的是从负向更为接近周期开始的数值。那么这里的 就只能是负的质数， 的取值为，

若从负向开始计数，大小顺序是从最大的质数 -1 开始，到小一点的 -2 ，然后是 -3 ，最小的是上一个周期中最开始的 1 。

把这种负质数带入泽塔函数的倒数，

此处提取前三项是因为最多取 3 个虚数单位的倒数，到第四个虚数单位四个相乘就等于 1 了。三个虚数单位的倒数相乘等于负数，事实上整个泽塔函数的结果就是负数。 3 ， 2 和 2 这三个看上去比较小的数，都是很大的数，例如 ，都是正数 1 减去一个上一个周期末尾的很大的数得到的负数，本质上是小数减大数。综合上述分析，

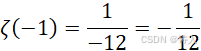
这里蕴含了，只要承认 N=0 ，就一定可以导出负数的结果。再观察，

首尾对应项相加为 0 ，那么一定有一个中间项，

也就是，，

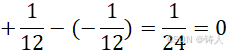
可见周期不只是 12 ，也可以是 24 。我们把这个数列和再写一遍，

它正是扩展黎曼泽塔函数的形式。而此时中间项不是 0 ，而是一个非零的结果。回顾上面的过程，我们之所以能得到这个非 0 的结果，是因为我们用三个虚数单位层次去观察周期 N 上的 -1 ， -2 ，以及所有更小的数值的乘积的综合结果，这三个最大的质数周期。能得到这个数值有两方面的原因，一方面是周期多大我们并不知道，而且不需要知道，另一方面是我们只能观察三个层，因为观察四个层次就构成了层次上的环绕。根据上面的分析，我们可以认为这个结构就是一个最简单的光子。它的频率核心也有正负，但是正负（看上去）是相等的。由此我们可以判定，可能存在“黑光子”，使得两个光子也可以纠缠在一起。

现在到了见证奇迹的时刻，自变量为 -1 的泽塔函数为什么具有无限多项，却能得到一个确定的值？

这是因为它本质上就是这种形式，

而只要相加的相继自然数涉及的质数多于 3 个，那么它的数值就决定于观察者对于虚数单位（此处为负质数）的理解，其实就是前两个质数 1 和 2 作为负质数的时候和 1 的差也就是 2 和 3 ，以及后面所有的质数和 1 的差也就是 2 ，这三个数就决定了这个函数在自变量为 -1 前提下的数值。用更直白的话说，只要你如此排列自然数，且如此观察自然数，用不了那么多个自然数，可能只需要三五个或者可以给出数百万个，但在这个前提下的结果都是一样的。当然太少了不行，最大的至少得大于等于 6 或者大于等于 8 ，不然用三个作为质数的虚数单位来观察这个序列就太多了，而且得不到这个结果。

这里的无限指的就是不被限制，具体的说就是泽塔函数的项数不受限制（其实还是有最小项数的要求），在超过最小项数之后不管再多多少项，观察者的最多三个正交维度（三个虚数单位），观察的结果都是一个（或者正负两个）确定的值。

如果这说的就是光子，那么可见哪怕核心频率（也就是 m ）是完全相同的，但它可以携带的谐波多少也是不一样的，甚至周期的正负也是有偏向的。虽然对于观察者来说，看上去并无区别。

从 Zeta(-1) 的构造我们可以了解到 s 的作用。它的作用其实就是维数的作用。正常来说维数是从不同的质数而来，有几个质数就有几个维数。 2 ， 3 ， 5 这些质数彼此互质，但这些质数能够体现出作用，还得由 s 来决定， s 决定那个导函数到底是什么函数，也就决定了原函数到底是什么函数。不同的函数起到不同的作用。

比如说，从频率或者周期上来看， A 是 B 的两倍，那么 A 看 B ， B 的单位 1 就是 A 的单位 1 的一半。所以 A 可以通过观察频率只有其一半的 B ，来使得 B 建立并且给 A 提供持久性。比如让 ，再选择某个特定的 构成，

就可以在 B 的层面上创造稳定的具有质量的物质。换句话说，如果不这样做的话，那么一切都是光子，是这种观察方式使得被观察者具有了各个谐波项上相互关联的能力。而如果被观察者不愿意，那么只需要避免和观察者的期望对齐即可。