注:本文为 “导航坐标系” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重,按需检索查阅。
如有内容异常,请看原文。
常见导航坐标系定义
bltly 原创于 2020-10-20 11:18:27 发布
常见坐标系概述
导航系统中常用的坐标系包括大地坐标系、地心惯性参考系、地心地固参考系、切平面坐标系及随体坐标系。其中,大地坐标系与地心惯性参考系属于非加速参考系,不随地球自转运动;地心地固坐标系与切平面坐标系随地球自转角速度同步转动;随体坐标系相对惯性参考系定义,用于描述航行器的运动姿态。
一、大地坐标系 WGS84(World Geodetic Coordinate System 1984)
该坐标系专为 GPS 全球定位系统构建,原点位于地球质心, Z Z Z 轴指向 BIH1984.0 定义的协定地球极(CTP)方向, X X X 轴指向 BIH1984.0 的零度子午面与 CTP 赤道的交点, Y Y Y 轴与 Z Z Z 轴、 X X X 轴构成右手坐标系。其描述参数为经度、纬度及海拔高度。
基本参数
- 长半径: a = 6378137 ± 2 (m) a = 6378137 \pm 2 \ \text{(m)} a=6378137±2 (m);
- 地球引力与地球质量的乘积: G M = 3986005 × 1 0 8 m 3 s − 2 ± 0.6 × 1 0 8 m 3 s − 2 GM = 3986005 \times 10^8 \ \text{m}^3\text{s}^{-2} \pm 0.6 \times 10^8 \ \text{m}^3\text{s}^{-2} GM=3986005×108 m3s−2±0.6×108 m3s−2;
- 正常化二阶带谐系数: C 20 = − 484.16685 × 1 0 − 6 ± 1.3 × 1 0 − 9 C_{20} = -484.16685 \times 10^{-6} \pm 1.3 \times 10^{-9} C20=−484.16685×10−6±1.3×10−9;
- 地球重力场二阶带球谐系数: J 2 = 108263 × 1 0 − 8 J_2 = 108263 \times 10^{-8} J2=108263×10−8;
- 地球自转角速度: ω = 7292115 × 1 0 − 11 rads − 1 ± 0.150 × 1 0 − 11 rads − 1 \omega = 7292115 \times 10^{-11} \ \text{rads}^{-1} \pm 0.150 \times 10^{-11} \ \text{rads}^{-1} ω=7292115×10−11 rads−1±0.150×10−11 rads−1;
- 扁率: f = 0.003352810664 f = 0.003352810664 f=0.003352810664。
二、地心惯性参考系 ECI(The Earth-Centered Inertial Frame) { i } \{i\} {i}
地心惯性坐标系是牛顿运动定律适用的非加速参考系,原点位于地心, o x ox ox 轴经过 0 ∘ 0^\circ 0∘ 经线与赤道的交点, o y oy oy 轴经过 9 0 ∘ 90^\circ 90∘ 经线与赤道的交点, o z oz oz 轴指向北极星方向。
三、地心地固参考系 ECEF(Earth-Centered, Earth-Fixed) { e } \{e\} {e}
ECEF 坐标系与地球固联且随地球同步转动,坐标原点 O O O 位于地球质心。 X X X 轴通过格林尼治子午线与赤道的交点,正方向由原点指向该交点; Z Z Z 轴通过原点指向北极; Y Y Y 轴与 X X X 轴、 Z Z Z 轴构成右手坐标系。
下图可直观呈现 ECEF 与 WGS84 坐标系的差异:

图中, φ \varphi φ(纬度)、 λ \lambda λ(经度)为 WGS84 坐标系的参数, x x x、 y y y、 z z z 为 ECEF 坐标系的描述参数,可清晰观察目标点 X X X 标记在不同坐标系下的描述差异
四、局部切线平面(北东地坐标系) { n } \{n\} {n}
局部切线平面定义于随航行器同步移动的地球表面切线平面上,按纵坐标方向可分为两类:纵坐标向上时为 ENU(东、北、天)坐标系,主要应用于地理领域;纵坐标向下时为 NED(北、东、地)坐标系,特别适用于航空航天领域。该坐标系又称导航坐标系,是日常生活中常用的坐标系,其 x x x 轴指向真北, y y y 轴指向东, z z z 轴垂直于地球表面且指向下方,通过经度 l l l 和纬度 μ \mu μ 进行辅助描述。

图为 ENU 坐标系,该坐标系即控制装置所在位置的“平面坐标系”,又称地理坐标系。
五、随体坐标系(Body Frame) { b } \{b\} {b}
随体坐标系相对惯性参考系(船舶领域中惯性参考系以 { e } \{e\} {e} 或 { n } \{n\} {n} 表示)描述船舶的位置与方向,船舶的线速度和角速度需在该坐标系中表征。通常将坐标原点 o b o_b ob 选在水面线中点(称为 CO),船舶的 x b x_b xb 轴、 y b y_b yb 轴、 z b z_b zb 轴与惯性主轴重合。
载体坐标系以载体质心为原点, O X OX OX 轴沿载体纵轴(前进方向), Z Z Z 轴沿载体侧轴(指向右翼), Y Y Y 轴沿载体竖轴(指向天),三者构成右手坐标系。载体坐标系与地理坐标系的相对关系即为载体的姿态,实际控制中需关注二者间的变换,常用的变换方式包括四元数、欧拉角及方向余弦矩阵,均是通过将地理坐标系转换至载体坐标系,实现对载体的姿态控制。
导航的基本要求是确保不同坐标系间的准确转换,避免误差,唯有如此,载体在自身坐标系中的一系列动作才能准确映射至地理坐标系中。
导航过程各坐标系之间转换
HX71 原创于 2018-10-13 17:06:16 发布
在导航技术实践中,坐标系间的转换是主要技术环节之一,其计算过程需严谨推导公式以保障精度。本文系统梳理导航常用坐标系的转换方法,为工程应用提供明确的技术参考。
一、经纬高(WGS84)转地心(ECEF)坐标系
经纬高坐标系(WGS84)与地心地固坐标系(ECEF)的转换基础,是将球面坐标(经度、纬度、海拔)映射为空间直角坐标。转换公式如下:
 (1)
(1)
式(1)中, φ \varphi φ 为纬度, λ \lambda λ 为经度, e e e 为地球椭圆率, h h h 为海拔高度, N N N 为卯酉圈曲率半径,其计算公式为 N = a 1 − e 2 sin 2 φ N = \frac{a}{\sqrt{1 - e^2\sin^2\varphi}} N=1−e2sin2φa( a a a 为地球长半径,参考 WGS84 基本参数)。该转换需先通过纬度计算曲率半径,再结合经度和海拔完成直角坐标换算。
二、地心(ECEF)转经纬高(WGS84)坐标系
地心坐标系到经纬高坐标系的转换为上述过程的逆运算,需通过迭代求解纬度,再计算经度和海拔,公式如下:
 (2)
(2)
式(2)中变量定义与式(1)一致。实际计算时,纬度 φ \varphi φ 需通过 z z z 坐标与水平距离的比值迭代求解,直至两次计算结果的偏差小于设定阈值(通常取 1 0 − 8 rad 10^{-8}\ \text{rad} 10−8 rad 量级),以保证转换精度。
三、东北天(ENU)坐标系转地心(ECEF)坐标系
东北天坐标系为局部切线平面坐标系,其原点与载体位置重合,而 ECEF 坐标系原点为地球质心,因此转换需包含坐标原点偏移和姿态旋转两个步骤。转换关系如下:
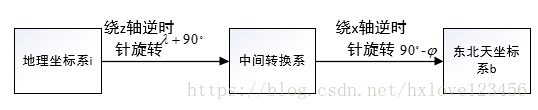
上式中, P E C E F \boldsymbol{P}_{ECEF} PECEF 为目标点的 ECEF 坐标, P E C E F 0 \boldsymbol{P}_{ECEF}^0 PECEF0 为东北天坐标系原点的 ECEF 坐标, R n − e \boldsymbol{R}_{n-e} Rn−e 为东北天坐标系到 ECEF 坐标系的旋转矩阵, P E N U \boldsymbol{P}_{ENU} PENU 为目标点的东北天坐标。
其中,旋转矩阵 R n − e \boldsymbol{R}_{n-e} Rn−e 由原点的纬度 φ \varphi φ 和经度 λ \lambda λ 确定,表达式为:
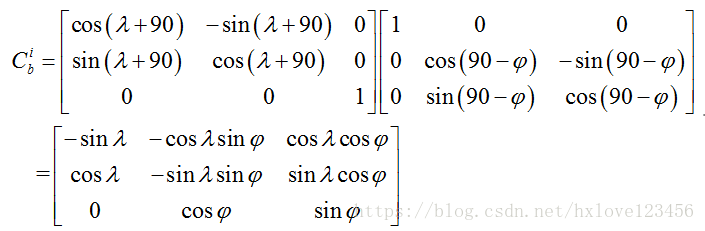
需特别注意,原点偏移量 P E C E F 0 \boldsymbol{P}_{ECEF}^0 PECEF0 是转换的关键参数,需先通过原点的经纬高坐标计算得到其对应的 ECEF 坐标,再参与后续运算。
四、地心(ECEF)转东北天(ENU)坐标系
该转换为东北天转地心的逆过程,是通过旋转矩阵的逆矩阵实现姿态反变换,并通过坐标差值消除原点偏移。转换公式如下:

由于旋转矩阵为正交矩阵,其逆矩阵等于转置矩阵。因此,只需将公式三中的旋转矩阵 R n − e \boldsymbol{R}_{n-e} Rn−e 进行转置,即可得到 ECEF 到东北天坐标系的旋转矩阵 R e − n \boldsymbol{R}_{e-n} Re−n,无需重新推导复杂运算。
五、载体(Body)坐标系转东北天(ENU)坐标系
载体坐标系与东北天坐标系的转换依赖于姿态角(翻滚角、俯仰角、偏航角)的定义。不同的角度定义方式会对应不同的旋转矩阵,但均遵循右手坐标系规则。以下为工程中常用的角度定义及对应转换方法。
1. 姿态角定义规范
本文采用导航领域通用的角度定义方式:
- 偏航角 ψ \psi ψ:载体纵轴与正北方向的夹角,顺时针旋转为正;
- 俯仰角 θ \theta θ:载体纵轴与水平面的夹角,逆时针(抬头)方向为正;
- 翻滚角 ϕ \phi ϕ:载体横轴与水平面的夹角,顺时针(右滚)方向为正。
该定义方式的旋转顺序为:先绕东北天坐标系的 z z z 轴(天向)旋转偏航角 ψ \psi ψ,再绕旋转后的 y y y 轴(东向)旋转俯仰角 θ \theta θ,最后绕旋转后的 x x x 轴(北向)旋转翻滚角 ϕ \phi ϕ。
2. 对应旋转矩阵推导
根据上述旋转顺序,载体坐标系到东北天坐标系的转换需通过三次基础旋转矩阵的乘积实现,最终状态转移矩阵如下:

3. 常见旋转矩阵差异说明
工程实践中可能遇到不同形式的旋转矩阵,差异源于偏航角正方向定义的不同。若将偏航角定义为“北偏西为正”(即逆时针旋转为正),旋转顺序不变的情况下,状态转移矩阵会发生如下变化:

这种形式的矩阵更为常见,需注意与角度定义的对应关系。此外,东北天坐标系到载体坐标系的转换矩阵,为上述矩阵的转置(因正交矩阵的逆等于转置),无需额外推导。
转换注意事项
- 参数一致性:所有转换中涉及的地球参数(长半径 a a a、椭圆率 e e e 等)需统一采用 WGS84 标准,避免参数混用导致误差;
- 迭代精度:地心转经纬高时,纬度的迭代求解需保证足够精度,避免误差累积影响后续导航计算;
- 矩阵方向:旋转矩阵的左乘与右乘需严格区分,确保坐标向量与矩阵的运算顺序符合“变换矩阵×原坐标=新坐标”的规则;
- 原点标识:局部坐标系(东北天、载体)与地心坐标系转换时,必须明确局部坐标系原点的地心坐标,避免遗漏原点偏移量。
通过明确上述转换规则及关键细节,可有效规避坐标系转换中的常见问题,为导航系统的姿态解算、位置定位提供可靠的技术支撑。
北东地/东北天两种导航坐标系与姿态转换
zht2370201 原创于 2019-04-15 16:06:54 发布
本文详细阐述了导航坐标系(北东地和东北天)与载体坐标系(前右下和右前上)的概念,介绍了姿态角的定义及其与坐标轴的关系,包括俯仰角、横滚角和航向角的范围与方向。同时,文中还探讨了导航坐标系与载体坐标系之间的姿态旋转矩阵,为理解载体运动提供了关键数学工具。
一、坐标系
1. 导航坐标系
导航领域中,北东地与东北天是两种应用广泛的导航坐标系,二者的坐标轴指向定义明确,具体如下:
1.1 北东地坐标系
-
X 轴:指向正北方向;
-
Y 轴:指向正东方向;
-
Z 轴:指向地球球心(即垂直地面向下)。
1.2 东北天坐标系
-
X 轴:指向正东方向;
-
Y 轴:指向正北方向;
-
Z 轴:指向天顶方向(即垂直地面向上)。
2. 载体坐标系
载体坐标系的定义通常与导航坐标系存在对应关系,常用的两种载体坐标系参数如下:
2.1 前右下坐标系——对应北东地导航坐标系
该坐标系以载体为参考,坐标轴指向与载体运动状态紧密关联:
-
X 轴:指向载体的前进方向;
-
Y 轴:指向载体的右侧方向;
-
Z 轴:指向载体的下方方向。
2.2 右前上坐标系——对应东北天导航坐标系
其坐标轴指向设计贴合载体操作与感知需求:
-
X 轴:指向载体的右侧方向;
-
Y 轴:指向载体的前进方向;
-
Z 轴:指向载体的上方方向。
二、姿态角/轴向/范围
姿态角是描述导航坐标系经过三次连续旋转后,与载体坐标系重合过程中的三个角度参数,是表征载体姿态的关键物理量。
1. 姿态角范围
为确保姿态描述的唯一性与规范性,各姿态角的取值范围被明确界定:
-
俯仰角:取值范围为 -90° ~ 90°,用于描述载体前后俯仰的程度;
-
横滚角:取值范围为 -180° ~ 180°,反映载体左右倾斜的状态;
-
航向角:基础取值范围为 -180° ~ 180°,实际应用中可通过换算转换为 0° ~ 360° 的范围,以明确载体的行进方向与正北方向的夹角。
2. 姿态角对应轴向
不同导航坐标系下,姿态角与坐标轴的对应关系存在差异,具体对应规则如下:
-
北东地坐标系:X 轴(正北)对应横滚角,Y 轴(正东)对应俯仰角,Z 轴(指向地心)对应航向角;
-
东北天坐标系:X 轴(正东)对应俯仰角,Y 轴(正北)对应横滚角,Z 轴(指向天顶)对应航向角。
3. 姿态角对应方向
姿态角的正负方向遵循右手定则,即四指沿旋转方向弯曲时,拇指指向为坐标轴正方向,则该旋转方向对应的姿态角为正。结合不同坐标系的特性,具体方向规则如下:
3.1 北东地坐标系
-
俯仰角与横滚角:姿态角方向与对应坐标轴的转动方向完全一致。当绕对应坐标轴正向旋转时,姿态角为正;绕坐标轴反向旋转时,姿态角为负;
-
航向角:以 X 轴指向正北为航向角零基准。当载体航向从正北向东北方向顺时针偏转时,航向角从 0° 逐渐增大至 360°,符合顺时针旋转为正的规则。
3.2 东北天坐标系
-
俯仰角与横滚角:与北东地坐标系规则一致,姿态角方向与对应坐标轴转动方向保持一致,绕轴正向旋转则姿态角为正,反向旋转则为负;
-
航向角:与对应坐标轴(Z 轴)的转动方向相反。这是因为东北天坐标系中,航向角的零基准为 Y 轴指向正北,且北偏东顺时针偏转时航向角增大,而 Z 轴指向天顶,只有当绕 Z 轴反向旋转时,才能与航向角的增大方向相匹配。
注意:东北天坐标系中航向角方向特殊的原因在于其定义基准——当 Y 轴指向正北时航向角为零,而航向角增大方向(北偏东顺时针)与 Z 轴(天顶)的正向旋转方向相反,只有绕 Z 轴反向旋转,航向角才会随顺时针偏转逐渐增大。
三、导航坐标系与载体坐标系之间的姿态旋转矩阵
姿态旋转矩阵是实现导航坐标系与载体坐标系之间坐标转换的数学工具,通过矩阵运算可精准描述两个坐标系的相对姿态关系。
姿态旋转矩阵(Attitude Rotation Matrix)是描述导航坐标系(Navigation Frame)与载体坐标系(Body Frame)之间空间关系的数学表达工具。其功能在于通过线性变换实现坐标系间的坐标转换,确保转换过程满足正交性(Orthogonality)和保角性(Angle-Preserving)的性质。具体而言,该矩阵由三个正交单位向量组成,分别对应两个坐标系的轴方向,从而精确描述其相对姿态(Relative Orientation)。在惯性导航(Inertial Navigation)、机器人运动学(Robot Kinematics)及计算机视觉(Computer Vision)等领域,姿态旋转矩阵广泛应用于坐标系转换、姿态估计(Attitude Estimation)及运动轨迹重建(Trajectory Reconstruction)等任务。
1. 基本旋转矩阵
若坐标系 1 绕其三个坐标轴依次旋转特定角度后得到坐标系 2,则从坐标系 1 到坐标系 2 的变换矩阵可由三个绕单轴旋转的基本矩阵相乘得到,基础表达式如下:

该矩阵的本质是将三次旋转的变换效果整合,矩阵中的元素由各旋转角度的三角函数值构成,可直接用于坐标向量的转换计算。
2. 北东地导航坐标系到前右下载体坐标系的旋转矩阵
北东地坐标系与前右下坐标系存在固定对应关系,其姿态旋转矩阵需结合横滚角(绕 X 轴)、俯仰角(绕 Y 轴)、航向角(绕 Z 轴)的旋转顺序推导,具体推导过程及最终矩阵形式如下:




应用该矩阵时,需将导航坐标系下的坐标向量左乘旋转矩阵,即可得到对应的载体坐标系坐标向量,实现两种坐标系的精准转换。
3. 东北天导航坐标系到右前上载体坐标系的旋转矩阵
东北天坐标系与右前上坐标系的转换,需依据俯仰角(绕 X 轴)、横滚角(绕 Y 轴)、航向角(绕 Z 轴)的特定旋转顺序推导旋转矩阵,完整的推导步骤及最终矩阵表达式如下:





由于旋转矩阵为正交矩阵,其逆矩阵等于转置矩阵。因此,若需实现前右下载体坐标系到北东地导航坐标系、右前上载体坐标系到东北天导航坐标系的逆转换,只需对上述对应旋转矩阵进行转置运算即可,无需重新推导。
导航坐标系变换关系
Barry_123 原创于 2021-05-07 22:13:08 发布
1. 常用坐标系定义
各坐标系的详细定义可参考
- 常见导航坐标系定义_北天东坐标系-优快云 博客
https://blog.youkuaiyun.com/bltly/article/details/109177418
以下仅进行简要罗列,不展开深入阐释。
1.1 地心惯性坐标系(Inertial Frame)
作为牛顿运动定律适用的参考坐标系,原点位于地球质心,坐标轴指向空间固定方向(如恒星方向),不随地球自转或公转运动。
1.2 地球坐标系(Earth Frame)
即 ECEF(地心地固坐标系,Earth-Centered Earth-Fixed),原点位于地球质心,坐标轴与地球固联并随地球同步自转,是描述地球表面及近地目标位置的常用坐标系。
1.3 地理坐标系(Geographic Frame)
即 LLA(经纬高坐标系,Longitude, Latitude, Altitude),通过经度(Longitude)、纬度(Latitude)和海拔高度(Altitude)三个参数描述目标在地球表面的位置,是日常导航与定位中最易理解的坐标系。
1.4 导航坐标系(Navigation Frame)
包括 ENU(东北天坐标系,East-North-Up)和 NED(北东地坐标系,North-East-Down)两种形式,均为局部切线平面坐标系,原点与载体位置重合,坐标轴与地理方向关联,是惯性导航系统求解导航参数的基础参考坐标系。
1.5 载体坐标系(Body Frame)
原点位于载体质心,坐标轴与载体结构固联(如前进方向、右侧方向、垂直方向),用于描述载体自身的运动状态(速度、加速度、姿态),其姿态相对导航坐标系的变化通过姿态角表征。
2. 坐标变换
2.1 LLA 到 ECEF 变换
经纬高坐标系(LLA)到地心地固坐标系(ECEF)的变换,本质是将球面坐标转换为空间直角坐标,变换公式如下:

式中, λ \lambda λ 为经度, φ \varphi φ 为纬度, h h h 为海拔高度, a a a 为地球长半径, e e e 为地球椭圆率, N N N 为卯酉圈曲率半径,其计算公式为 N = a 1 − e 2 sin 2 φ N = \frac{a}{\sqrt{1 - e^2\sin^2\varphi}} N=1−e2sin2φa(参数取值参考 WGS84 标准)。
2.2 ECEF 到 LLA 变换
地心地固坐标系(ECEF)到经纬高坐标系(LLA)的变换为上述过程的逆运算,需通过迭代方法求解纬度,再计算经度和海拔高度,变换公式如下:

式中, x x x、 y y y、 z z z 为 ECEF 坐标系下的坐标值,其他参数定义与 2.1 节一致。迭代求解纬度时,需保证计算精度满足导航需求(通常迭代误差小于 1 0 − 8 rad 10^{-8}\ \text{rad} 10−8 rad)。
2.3 ENU/NED 到 ECEF 变换
ENU(东北天)和 NED(北东地)均属于导航坐标系,是惯性导航系统求解导航参数时采用的参考坐标系。导航坐标系到地心地固坐标系(ECEF)的位置变换需分为两步:
- 先将导航坐标系原点的 LLA 坐标转换为 ECEF 坐标(即通过 2.1 节 LLA to ECEF 变换实现);
- 再通过旋转矩阵将导航坐标系下的相对坐标转换为 ECEF 坐标系下的绝对坐标,姿态变换关系详见下文 3.2 节。
相关实现代码可参考开源项目:
3. 姿态变换
3.1 ENU 到 NED 变换
ENU(东北天)与 NED(北东地)坐标系均为局部导航坐标系,二者的区别仅在于坐标轴的指向(Z 轴分别指向天顶和地心,X 轴、Y 轴指向顺序不同),其姿态变换可通过固定旋转矩阵实现,变换公式如下:

该矩阵通过调整坐标轴的正负方向和顺序,实现两种导航坐标系间的坐标映射,变换过程无信息损失,逆变换矩阵与原矩阵相同(因矩阵为正交矩阵且满足自逆特性)。
3.2 NED 到 ECEF 变换
北东地坐标系(NED)到地心地固坐标系(ECEF)的姿态变换,是通过旋转矩阵描述两个坐标系的相对姿态关系。该旋转矩阵由 NED 坐标系原点的纬度 φ \varphi φ 和经度 λ \lambda λ 确定。
具体推导过程及变换公式如下:



上述公式参考国外硕士论文《FLIGHT PLAN GENERATION FOR UNMANNED AERIAL VEHICLES》(原文部分符号存在误差,使用时需注意校验),论文链接:FLIGHT PLAN GENERATION FOR UNMANNED AERIAL VEHICLES。
姿态变换的逻辑是:通过绕 ECEF 坐标系的坐标轴旋转,将 NED 坐标系的坐标轴与 ECEF 坐标系的坐标轴对齐,旋转矩阵的元素由三角函数构成,反映了地理方向与地心直角坐标方向的映射关系。
参考文章
地图坐标系大全:常用地图坐标系详解与转换指南
言之兮兮 原创于 2023-02-18 11:21:00 发布
一、地图坐标系的基本概念和原理
地图坐标系是描述地图上位置的数学模型,可精确定位地球表面任意点的位置。不同坐标系基于不同基准面与投影方式设计,参数存在差异,因此坐标系间的转换是应用中的关键环节,在地图制图、导航、GIS 等领域具有重要作用。
地球是近似椭球体的三维物体,其形状与尺寸复杂,需通过数学模型简化描述以实现位置测量。建立地图坐标系主要依赖基准面与投影方式两大要素:
- 基准面:作为位置参考的基础面,分为椭球体与大地水准面两类。椭球体通过长半轴、短半轴参数近似模拟地球形状;大地水准面则以平均海平面为基准,反映地球真实重力场分布。
- 投影方式:将三维地球表面映射到二维平面的方法,不同投影方式会导致地图上区域形状、面积的变形程度不同,需根据应用场景选择适配的投影类型。
二、常见的地图坐标系类型
2.1 地球经纬度坐标系
地球经纬度坐标系属于球面坐标系,通过经度与纬度确定地球表面位置,将地球划分为东西半球(以本初子午线为界)与南北半球(以赤道为界)。
- 经度:取值范围-180°~180°,0°经线为英国伦敦格林威治天文台的本初子午线,东经为正、西经为负;
- 纬度:取值范围-90°~90°,赤道为 0°纬线,北纬为正、南纬为负。
该坐标系直观易懂、计算简便,但因地球为球体,在地图制图与空间分析中需进行坐标变换以适配平面应用场景。
2.2 平面直角坐标系(以 UTM 坐标系为例)
平面直角坐标系适用于较小地理区域(如城市、州域),将地球表面划分为网格,通过唯一坐标值定位。UTM 坐标系是典型代表,将地球分为 60 个纵向带与 6 个横向带,每个带采用横向或纵向墨卡托投影,以假东、假北坐标表示位置。
相比经纬度坐标系,平面直角坐标系在短距离内精度更高,适用于测量、地图绘制等领域,但长距离应用会产生较大投影误差,不适用于大范围导航与测量。
2.3 地方坐标系(以高斯-克吕格坐标系为例)
地方坐标系基于局部大地基准建立,坐标轴多为平面直角坐标系,需结合地球椭球形状与大地基准差异实现与全球坐标系的转换。高斯-克吕格坐标系(高斯投影坐标系)是常见类型,将地球划分为带状区域,中国通常采用六度带(带宽 6°,以中央经线为中心向东西各延伸 3°)。
该坐标系以 1954 年北京坐标系(BJS54)为大地基准,需先将 WGS-84 经纬度坐标转换至 BJS54 坐标系,再转换为高斯-克吕格坐标。其优势在于坐标处理便捷、小区域投影误差小、相对精度高,但不适用于跨投影带场景,大范围应用时误差显著。
2.4 地心坐标系(以 WGS-84 坐标系为例)
地心坐标系以地球质心为原点,地球自转轴为 Z 轴,适用于描述地球物理特性、导航定位等场景。WGS-84 坐标系是应用最广泛的地心坐标系,基于国际地球参考系(ITRF)构建,通过数学模型与测量数据刻画地球形状与旋转规律。
WGS-84 为三维坐标系,坐标轴定义为:X 轴指向经度 0°、纬度 0°交点;Y 轴指向经度 90°E、纬度 0°点;Z 轴与地球自转轴重合指向北极点。地球形状抽象为椭球体(长半轴 6378137 米,短半轴 6356752.3142 米,离心率 0.0818191910428),经纬度坐标可转换为 XYZ 坐标实现位置计算与导航。
2.5 百度坐标系
百度坐标系(BD-09 坐标系)由百度自主设计,基于 WGS-84 坐标系加入加密算法,专用于百度地图及相关应用。其与 WGS-84 的差异体现在坐标加密与误差微调,通过随机偏移量与加密算法保障位置信息安全,坐标原点与 WGS-84 一致但计算转换方式不同。
转换时需先将 WGS-84 经纬度转换为百度坐标系经纬度,再经加密微调得到最终坐标。由于该坐标系非国际通用,与其他坐标系转换时需注意误差控制。
2.6 腾讯地图坐标系
腾讯地图采用 Web 墨卡托投影的平面直角坐标系,定义如下:
- 原点:赤道与本初子午线交点;
- X 轴:经度线方向(单位:米);
- Y 轴:纬度线方向(单位:米);
- 范围:
X 轴[-20037508.3427892, 20037508.3427892],
Y 轴[-20037508.3427892, 20037508.3427892]。
该坐标系与百度地图坐标系同为 Web 墨卡托投影,属于平面坐标系,在地图显示、距离与面积计算时需进行坐标系转换。
2.7 OpenStreetMap 坐标系
OpenStreetMap 直接采用 WGS-84 坐标系,遵循国际通用标准,便于与全球定位系统及其他 GIS 系统兼容。
三、每种坐标系的具体介绍
3.1 地球经纬度坐标系
3.1.1 定义和用途
定义:通过经度与纬度确定球面位置的坐标系,用于表示地球表面任意点。
用途:描述自然地理特征(山脉、河流、海洋)与人工地理特征(城市、行政边界),广泛应用于导航、航海、GIS 制图、空间分析与查询。
3.1.2 投影方式
作为球面坐标系,需投影为二维平面坐标系使用,常用方式包括:
- 经纬度网格:直接以经纬线划分平面,极区变形显著;
- 墨卡托投影:保角投影,适用于航海导航;
- 等距圆柱投影:保持距离比例,适用于小区域地图。
3.1.3 基准面
通用基准面为 WGS-84 椭球体,其形状与尺寸匹配地球实际特征,全球适用性强。
3.1.4 坐标表示和转换方法
表示形式:度分秒(DMS,如 106°32’23")与十进制度(DD,如 106.54°);
转换方法:需通过投影算法转换为平面坐标,或通过地心坐标系实现与其他坐标系的映射。
3.1.5 优缺点和适用范围
优点:直观易懂、全球通用;
缺点:球面坐标不便于平面计算,极区投影变形大;
适用范围:全球范围的定位、导航与地理信息标注。
3.2 平面直角坐标系
3.2.1 定义和用途
定义:基于平面直角坐标系的局部坐标系统,将地球表面局部区域投影为平面;
用途:小区域地图制图、工程测量、城市定位。
3.2.2 投影方式
常用投影包括横轴墨卡托投影、高斯-克吕格投影、UTM 投影,适配不同地区地形特征。
3.2.3 基准面
采用特定参数的椭球面(如国际 1924 年椭球、WGS-84 椭球)或平面作为基准面。
3.2.4 坐标表示和转换方法
表示形式:x、y 二维坐标值,或距离与方位角;
转换方法:通过正反算法实现经纬度与平面坐标的互转。
3.2.5 优缺点和适用范围
优点:计算简单、精度高、处理便捷;
缺点:大范围应用存在面积变形与方向畸变;
适用范围:城市地图、建筑设计、局部导航定位。
3.3 地方坐标系
3.3.1 定义和用途
定义:根据国家或地区需求,结合特定投影与基准面建立的坐标系;
用途:小面积区域测量、制图,是经纬度坐标系与平面直角坐标系的过渡体系,适用于国内传统 GIS 应用。
3.3.2 投影方式
采用等角圆锥投影、等距圆锥投影、兰伯特投影等,根据区域需求选择。
3.3.3 基准面
以国家或地区的大地水准面为基准(如中国 1975 国家基准面)。
3.3.4 坐标表示和转换方法
表示形式:横坐标、纵坐标;
转换方法:七参数法、四参数法实现不同坐标系间的转换。
3.3.5 优缺点和适用范围
优点:小区域精度高;
缺点:跨区域适配性差,坐标系间转换复杂;
适用范围:城市规划、工程测量、地方地图制图。
3.4 地心坐标系
3.4.1 定义和用途
定义:以地球质心为原点的三维直角坐标系;
用途:卫星导航系统、空间探测、地球物理学研究,精准描述地球表面及空间三维位置。
3.4.2 投影方式
采用球形坐标系或椭球坐标系表示。
3.4.3 基准面
以地球质心为基准,区别于其他坐标系的大地水准面或椭球面基准。
3.4.4 坐标表示和转换方法
表示形式:X、Y、Z 三维坐标(单位:米),常见坐标系包括 WGS-84、ITRF;
转换方法:需进行坐标变换、地球自转模型计算、大气延迟与相对论效应校正等复杂运算。
3.4.5 优缺点和适用范围
优点:精准描述地球及空间位置;
缺点:与地球表面无直接关联,需转换为地面坐标系才能用于表面测量;
适用范围:卫星导航、空间探测、地球物理研究。
3.5 百度坐标系
3.5.1 定义和用途
定义:百度基于 WGS-84 设计的专用坐标系(BD-09);
用途:百度地图的显示、定位服务。
3.5.2 投影方式
采用墨卡托投影将地球表面投影至二维平面。
3.5.3 基准面
以 WGS-84 椭球体为基准(长轴 6378137 米,短轴 6356752.3142 米,扁率 1/298.257223563)。
3.5.4 坐标表示和转换方法
表示形式:平面直角坐标(以北京海淀区西北旺为原点,单位:米);
转换方法:通过百度 API 实现与其他坐标系的转换。
3.5.5 优缺点和适用范围
优点:中国城市地理信息显示精度高;
缺点:与其他地图服务交互需 API 转换,兼容性差;
适用范围:中国地区的百度地图应用。
3.6 腾讯地图坐标系
3.6.1 定义和用途
定义:基于 Web 墨卡托投影的平面坐标系,将地球划分为矩形网格;
用途:Web 与移动应用中的地图数据检索与展示。
3.6.2 投影方式
墨卡托投影,保证面积与长度比例关系,提升地图可视性。
3.6.3 基准面
以 WGS-84 椭球体为基准,与 GPS 及主流 GIS 系统兼容。
3.6.4 坐标表示和转换方法
表示形式:(x, y) 二元组(相对于左上角网格的偏移量);
转换方法:通过 proj4、gdal 等开源库实现与经纬度坐标系的转换。
3.6.5 优缺点和适用范围
优点:数据检索与渲染速度快;
缺点:大范围或极区投影变形大,不适用于高精度测量;
适用范围:Web 与移动地图应用。
四、坐标系之间的转换方法
4.1 经纬度与平面坐标系之间的转换
转换要领为投影转换,步骤如下:
- 经纬度转地心空间直角坐标系(如 WGS-84);
- 地心坐标转局部平面直角坐标系(如 UTM、高斯-克吕格);
- 经投影转换(墨卡托、高斯-克吕格等)得到平面坐标。
平面坐标转经纬度则反向操作,先转局部平面直角坐标系,再转地心坐标系,最终转换为经纬度。
代码示例(Proj 库实现经纬度转 UTM 坐标):
#include <stdio.h>
#include "proj_api.h"
int main() {
projPJ pj_utm, pj_latlong;
double x, y;
double lat = 40.748817, lon = -73.985428; // 纽约时代广场经纬度
// 定义投影方式
pj_latlong = pj_init_plus("+proj=latlong +datum=WGS84");
pj_utm = pj_init_plus("+proj=utm +zone=18 +datum=WGS84");
// 坐标转换
pj_transform(pj_latlong, pj_utm, 1, 1, &lon, &lat, NULL);
printf("UTM 坐标为: %.3f, %.3f\n", lon, lat);
// 释放资源
pj_free(pj_latlong);
pj_free(pj_utm);
return 0;
}
4.2 平面坐标系之间的转换
需考虑原始坐标系与目标坐标系的表示方法、投影关系、精度控制,常用转换类型包括:
- 高斯-克吕格坐标系间转换;
- UTM 坐标系间转换;
- Web 墨卡托与经纬度坐标系转换;
- 百度/腾讯坐标系与经纬度坐标系转换。
转换算法包括高斯正反算法、UTM 投影算法、双线性插值算法等。
代码示例(Proj 库实现 BD-09 与 WGS-84 互转):
#include <proj_api.h>
#include <math.h>
// BD-09 转 WGS-84
void bd09_to_wgs84(double *lon, double *lat) {
projPJ pj_merc, pj_latlong;
char src[] = "+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m +no_defs";
char dst[] = "+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs";
pj_merc = pj_init_plus(src);
pj_latlong = pj_init_plus(dst);
double x = *lon, y = *lat;
pj_transform(pj_merc, pj_latlong, 1, 1, &x, &y, NULL);
*lon = x;
*lat = y;
pj_free(pj_merc);
pj_free(pj_latlong);
}
// WGS-84 转 BD-09
void wgs84_to_bd09(double *lon, double *lat) {
projPJ pj_latlong, pj_merc;
char src[] = "+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs";
char dst[] = "+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m +no_defs";
pj_latlong = pj_init_plus(src);
pj_merc = pj_init_plus(dst);
double x = *lon, y = *lat;
pj_transform(pj_latlong, pj_merc, 1, 1, &x, &y, NULL);
double z = sqrt(x * x + y * y) + 0.00002 * sin(y * M_PI);
double theta = atan2(y, x) + 0.000003 * cos(x * M_PI);
*lon = theta * 180.0 / M_PI;
*lat = z * sin(theta) * 180.0 / M_PI;
pj_free(pj_latlong);
pj_free(pj_merc);
}
4.3 地心坐标系和地方坐标系之间的转换
需结合基准面与投影方式差异,常用方法包括:
- 直接转换法:通过大地测量参数与公式直接转换,计算简单但精度有限;
- 基准面转换法:将两者转换至同一基准面(如 WGS-84)后再转换,精度高但需额外参数;
- 双向转换法:经纬度坐标系作为中介实现转换,精度高但计算量大。
基准面转换法需注意:选择 Helmert 七参数或 Molodensky-Badekas 七参数模型,统一椭球体参数,调整投影中央子午线,转换大地高程与正常高程。
4.4 不同地图服务之间坐标系的转换
不同地图服务坐标系差异需通过 API 或算法转换,示例如下:
4.4.1 Google Maps 经纬度转百度坐标系
import requests
def google_to_baidu(lng, lat):
url = 'http://api.map.baidu.com/geoconv/v1/'
params = {
'coords': f'{lng},{lat}',
'from': '1',
'to': '5',
'ak': 'your_baidu_map_api_key'
}
response = requests.get(url, params=params)
result = response.json()
if result['status'] == 0:
return result['result'][0]['x'], result['result'][0]['y']
else:
return None
4.4.2 高德地图经纬度转百度坐标系
import requests
def gaode_to_baidu(lng, lat):
url = 'http://api.map.baidu.com/geoconv/v1/'
params = {
'coords': f'{lng},{lat}',
'from': '3',
'to': '5',
'ak': 'your_baidu_map_api_key'
}
response = requests.get(url, params=params)
result = response.json()
if result['status'] == 0:
return result['result'][0]['x'], result['result'][0]['y']
else:
return None
4.4.3 腾讯地图经纬度转百度坐标系
import requests
def tencent_to_baidu(lng, lat):
url = 'http://api.map.baidu.com/geoconv/v1/'
params = {
'coords': f'{lng},{lat}',
'from': '3',
'to': '5',
'ak': 'your_baidu_map_api_key'
}
response = requests.get(url, params=params)
result = response.json()
if result['status'] == 0:
return result['result'][0]['x'], result['result'][0]['y']
else:
return None
五、坐标系的应用场景
5.1 GPS 定位和导航
GPS 系统通过卫星信号计算接收器位置,常用经纬度坐标系与平面直角坐标系。需将经纬度投影至平面坐标系以简化计算,同时进行坐标系转换与纠偏(如 WGS-84 转 GCJ-02、百度坐标系),提升定位精度。
5.2 地图绘制和渲染
地图绘制需将地理要素位置转换为对应坐标系坐标,不同地图应用采用的坐标系不同,需进行转换适配(如 WGS-84 转百度坐标系)以保证要素位置准确。
5.3 大地测量和工程测量
大地测量中,坐标系用于表示测量点位置,计算距离、方位角等参数,支撑工程设计与建设(如道路曲率、建筑物垂直度测量);工程测量则通过坐标系确定构件位置,保障基础设施建设精度。
5.4 地理信息系统(GIS)和遥感技术
GIS 融合多种坐标系数据进行管理与分析,遥感技术采集的地理数据(如数字高程模型、卫星图像)需通过坐标系表示与处理,实现数据分析、特征提取与地图绘制。
六、坐标系的发展历程和未来趋势
6.1 地图坐标系的起源和发展历史
地图坐标系起源于早期制图实践,古希腊欧几里德的平面直角坐标系奠定理论基础;17 世纪皮埃尔·费马提出地球椭球体概念;19 世纪工业革命推动坐标系应用扩展;20 世纪计算机与卫星导航技术加速坐标系发展,形成多样化的现代坐标系体系。
6.2 新的坐标系的提出和应用
随着测量技术进步,新型坐标系不断涌现:
- 国际地球参考系(ITRS):1994 年推出,作为全球导航、地震学等领域的基准;
- WGS-84 坐标系:GPS 系统专用,是全球应用最广泛的地心坐标系;
- UTM 坐标系:适用于军事、航空、测绘的平面直角坐标系;
- CGCS2000 坐标系:中国自主研制的大地坐标系,推动测绘技术现代化。
6.3 人工智能、云计算、大数据等技术对坐标系的影响和应用
- 人工智能:自动识别遥感图像特征,提取地理信息;
- 云计算:提升坐标系转换、大地测量的计算效率,实现数据共享协同;
- 大数据:整合多源地理数据,优化坐标系精度与覆盖范围,支撑地理信息领域创新发展。
惯性导航 惯性坐标系转换理解
~光~~ 原创于 2024-07-24 10:19:07 发布
一、惯性导航中惯性器件的测量特性
在惯性导航系统中,加速度计与陀螺仪等惯性器件的测量数据均基于载体系(b 系)输出,具体测量对象如下:
- 加速度计:测量载体在载体系(b 系)下的三维加速度矢量;
- 陀螺仪:测量载体在载体系(b 系)下的三维角速度矢量。
上述原始测量数据需通过多步坐标转换与导航解算,最终输出载体在惯性系(i 系)中的速度与位置参数,为导航控制提供基础数据支持。
二、“b 系相对于 i 系在 n 系的投影” 的内涵解析
2.1 术语定义与表述差异
“b 系相对于 i 系在 n 系的投影” 与 “b 系在 n 系的投影” 为两个相关但不同的概念,区别在于是否明确惯性系(i 系)的中间作用:
- b 系相对于 i 系在 n 系的投影:完整描述为 “载体在惯性系中的运动状态,经转换后投影至导航系”,需依次经过 “i 系→b 系→n 系” 的转换流程,符合惯性导航的解算逻辑;
- b 系在 n 系的投影:简化表述为直接将载体系运动状态转换至导航系,未明确惯性系的中间介导作用,易忽略惯性导航的关键解算环节。
2.2 采用完整表述的必要性
惯性导航系统中优先使用 “b 系相对于 i 系在 n 系的投影” 这一表述,主要基于以下技术考量:
1.参考系标准化:惯性系(i 系)为非旋转、无加速度的理想参考系(如地心惯性系 ECI),为不同坐标系间的转换提供统一基准,确保转换逻辑的一致性;
2.误差控制需求:通过惯性系作为中间过渡,可更精准地处理地球自转、载体姿态变化等带来的误差,减少累积误差对导航精度的影响;
3.系统设计逻辑:惯性导航系统的解算模型本质上基于惯性系构建,运动方程的推导与积分均以惯性系为基础,自然包含惯性系转换环节。
2.3 不直接使用 C b n C_{bn} Cbn 转换的技术原因
理论上,方向余弦矩阵
C
b
n
C_{bn}
Cbn 可直接实现载体系(b 系)到导航系(n 系)的转换,但工程实践中极少采用,原因如下:
1.解算复杂度优化:惯性系的中间作用可将多参考系转换分解为 “惯性系→载体系” 与 “载体系→导航系” 两步简单转换,避免直接转换带来的复杂矩阵运算;
2.误差累积抑制:经惯性系中转时,可通过陀螺仪输出的角速度实时更新姿态矩阵,及时校正姿态漂移,有效控制误差累积;
3.系统兼容性保障:主流惯性导航系统的硬件设计与软件算法均基于惯性系解算架构,保留惯性系中间环节可提升系统的可维护性与扩展性。
三、投影过程的具体含义与实例验证
3.1 概念界定
进行投影转换前,需明确三个关键坐标系的定义:
- 惯性系(i 系):本文采用地心惯性系(ECI),原点位于地球质心,坐标轴指向天球固定恒星,无旋转与加速度;
- 载体系(b 系):与载体固联的右手坐标系,X 轴指向载体前进方向,Y 轴指向载体右侧,Z 轴垂直于载体平面(符合右手法则);
- 导航系(n 系):本文采用东北天坐标系(ENU),原点位于载体当前位置,X 轴指向东,Y 轴指向北,Z 轴指向天顶。
3.2 投影转换的逻辑
“b 系相对于 i 系在 n 系的投影” 本质是载体速度矢量的坐标系转换过程,已知条件与转换步骤如下:
已知条件
- 载体在惯性系(i 系)中的速度矢量 v i \mathbf {v}_i vi;
- 载体系到惯性系的方向余弦矩阵 C b i C_{bi} Cbi(描述 b 系相对于 i 系的姿态);
- 导航系到惯性系的方向余弦矩阵 C n i C_{ni} Cni(描述 n 系相对于 i 系的姿态)。
转换步骤
1.步骤 1:惯性系速度转换至载体系
方向余弦矩阵的逆矩阵等于其转置矩阵(正交矩阵特性),因此载体系速度
v
b
\mathbf {v}_b
vb 可通过
C
b
i
T
C_{bi}^T
CbiT 计算:
v
b
=
C
b
i
T
⋅
v
i
\mathbf {v}_b = C_{bi}^T \cdot \mathbf {v}_i
vb=CbiT⋅vi
2.步骤 2:载体系速度转换至导航系
首先通过
C
n
i
C_{ni}
Cni 与
C
b
i
T
C_{bi}^T
CbiT 推导载体系到导航系的方向余弦矩阵
C
n
b
=
C
n
i
⋅
C
b
i
T
C_{nb} = C_{ni} \cdot C_{bi}^T
Cnb=Cni⋅CbiT,再计算导航系速度
v
n
\mathbf {v}_n
vn:
v
n
=
C
n
b
⋅
v
b
\mathbf {v}_n = C_{nb} \cdot \mathbf {v}_b
vn=Cnb⋅vb
3.3 实例计算验证
已知参数
- 惯性系速度矢量: v i = [ 200 150 100 ] m/s \mathbf {v}_i = \begin {bmatrix} 200 \\ 150 \\ 100 \end {bmatrix} \text { m/s} vi= 200150100 m/s
- 载体系到惯性系的转换矩阵: C b i = [ 0.866 0.5 0 − 0.5 0.866 0 0 0 1 ] C_{bi} = \begin {bmatrix} 0.866 & 0.5 & 0 \\ -0.5 & 0.866 & 0 \\ 0 & 0 & 1 \end {bmatrix} Cbi= 0.866−0.500.50.8660001
- 导航系到惯性系的转换矩阵: C n i = [ 0.36 0.48 − 0.8 − 0.8 0.6 0 0.48 0.64 0.6 ] C_{ni} = \begin {bmatrix} 0.36 & 0.48 & -0.8 \\ -0.8 & 0.6 & 0 \\ 0.48 & 0.64 & 0.6 \end {bmatrix} Cni= 0.36−0.80.480.480.60.64−0.800.6
计算过程
1.步骤 1:计算 v b \mathbf {v}_b vb
先求 C b i C_{bi} Cbi 的转置矩阵:
C b i T = [ 0.866 − 0.5 0 0.5 0.866 0 0 0 1 ] C_{bi}^T = \begin {bmatrix} 0.866 & -0.5 & 0 \\ 0.5 & 0.866 & 0 \\ 0 & 0 & 1 \end {bmatrix} CbiT= 0.8660.50−0.50.8660001
再计算载体系速度:
v b = C b i T ⋅ v i = [ 0.866 × 200 − 0.5 × 150 0.5 × 200 + 0.866 × 150 0 × 200 + 0 × 150 + 1 × 100 ] = [ 98.2 229.9 100 ] m/s \mathbf {v}_b = C_{bi}^T \cdot \mathbf {v}_i = \begin {bmatrix} 0.866 \times 200 - 0.5 \times 150 \\ 0.5 \times 200 + 0.866 \times 150 \\ 0 \times 200 + 0 \times 150 + 1 \times 100 \end {bmatrix} = \begin {bmatrix} 98.2 \\ 229.9 \\ 100 \end {bmatrix} \text { m/s} vb=CbiT⋅vi= 0.866×200−0.5×1500.5×200+0.866×1500×200+0×150+1×100 = 98.2229.9100 m/s
2.步骤 2:计算 C n b C_{nb} Cnb
依据 C n b = C n i ⋅ C b i T C_{nb} = C_{ni} \cdot C_{bi}^T Cnb=Cni⋅CbiT,矩阵乘法计算如下:
C n b = [ 0.36 0.48 − 0.8 − 0.8 0.6 0 0.48 0.64 0.6 ] ⋅ [ 0.866 − 0.5 0 0.5 0.866 0 0 0 1 ] = [ 0.55176 0.23568 − 0.8 − 0.3928 0.9196 0 0.73568 0.31424 0.6 ] \begin{aligned}C_{nb} &= \begin {bmatrix} 0.36 & 0.48 & -0.8 \\ -0.8 & 0.6 & 0 \\ 0.48 & 0.64 & 0.6 \end {bmatrix} \cdot \begin {bmatrix} 0.866 & -0.5 & 0 \\ 0.5 & 0.866 & 0 \\ 0 & 0 & 1 \end {bmatrix} \\&= \begin {bmatrix} 0.55176 & 0.23568 & -0.8 \\ -0.3928 & 0.9196 & 0 \\ 0.73568 & 0.31424 & 0.6 \end {bmatrix}\end{aligned} Cnb= 0.36−0.80.480.480.60.64−0.800.6 ⋅ 0.8660.50−0.50.8660001 = 0.55176−0.39280.735680.235680.91960.31424−0.800.6
3.步骤 3:计算 v n \mathbf {v}_n vn
导航系速度为:
v n = C n b ⋅ v b = [ 0.55176 × 98.2 + 0.23568 × 229.9 − 0.8 × 100 − 0.3928 × 98.2 + 0.9196 × 229.9 + 0 × 100 0.73568 × 98.2 + 0.31424 × 229.9 + 0.6 × 100 ] = [ 28.35 172.82 168.53 ] m/s \mathbf {v}_n = C_{nb} \cdot \mathbf {v}_b = \begin {bmatrix} 0.55176 \times 98.2 + 0.23568 \times 229.9 - 0.8 \times 100 \\ -0.3928 \times 98.2 + 0.9196 \times 229.9 + 0 \times 100 \\ 0.73568 \times 98.2 + 0.31424 \times 229.9 + 0.6 \times 100 \end {bmatrix} = \begin {bmatrix} 28.35 \\ 172.82 \\ 168.53 \end {bmatrix} \text { m/s} vn=Cnb⋅vb= 0.55176×98.2+0.23568×229.9−0.8×100−0.3928×98.2+0.9196×229.9+0×1000.73568×98.2+0.31424×229.9+0.6×100 = 28.35172.82168.53 m/s
结果说明
最终得到的导航系速度 v n \mathbf {v}_n vn 即为 “b 系相对于 i 系在 n 系的投影” 结果,该速度矢量直接反映载体在东北天坐标系中的运动状态,可用于后续导航定位解算。
常用导航坐标系及转换关系(理论+程序)
他人是一面镜子,保持谦虚 …原创已于 2022-02-23 21:34:01 修改

一、坐标系定义与符号约定
在捷联惯导系统中,需通过多种坐标系描述载体运动状态,坐标系的定义与特性如下:
1.1 惯性坐标系(i 系)
- 定义:以地球质心为原点,Z 轴指向地球自转轴,X 轴位于赤道面指向空间固定点,Y 轴与 X、Z 轴构成右手坐标系。
- 特性:不随地球自转运动,虽因地球公转存在微小加速度,但该影响低于惯导系统噪声水平,可近似视为理想惯性系。
1.2 地心地固坐标系(e 系)
- 定义:与大地测量中的 ECEF 坐标系一致,原点位于地球质心,坐标轴与地球固联并随地球自转。
- 转换关系:载体在 e 系中的坐标可通过方向余弦矩阵(DCM)转换至 i 系表示,实现不同参考系下位置参数的映射,其表达如下:
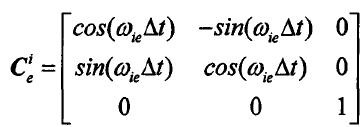

1.3 地理坐标系
- 定义:基于三维球面的坐标系,通过经纬度描述地球表面位置,包含角度测量单位、本初子午线、参考椭球体三个要素。
- 特性:以参考椭球体为基础构建经纬网,不可直接用于长度与面积测量(度为角度单位),需通过投影转换为平面坐标系。
- 与 e 系的转换:地理坐标系(经纬度+高程)与 e 系(直角坐标)可通过椭球参数计算实现双向转换,具体公式如下:

转换程序实现:
Eigen::MatrixXd llh2ecef(Eigen::MatrixXd data) // 经纬度转地心地固坐标
{
Eigen::MatrixXd ecef;
ecef.resize(3, 1);
double a = 6378137.0; // WGS-84 长半轴
double b = 6356752.314; // WGS-84 短半轴
double n, Rx, Ry, Rz;
double lon = data(0) * M_PI / 180.0; // 经度转弧度
double lat = data(1) * M_PI / 180.0; // 纬度转弧度
double alt = data(2); // 高程
n = a * a / sqrt(a * a * cos(lat) * cos(lat) + b * b * sin(lat) * sin(lat));
Rx = (n + alt) * cos(lat) * cos(lon);
Ry = (n + alt) * cos(lat) * sin(lon);
Rz = (b * b / (a * a) * n + alt) * sin(lat);
ecef << Rx, Ry, Rz;
return ecef;
/**************for test purpose*************************
Eigen::MatrixXd llh;
llh.resize(3, 1);
Eigen::MatrixXd ecef;
ecef.resize(3, 1);
llh(0) = 114.1772621294604;
llh(1) = 22.29842880200087;
llh(2) = 58;
ecef = llh2ecef(llh);
cout << "ecef ->: " << ecef << "\n";
*/
}
Eigen::MatrixXd ecef2llh(Eigen::MatrixXd data) // 地心地固坐标转经纬度
{
Eigen::MatrixXd llh;
llh.resize(3, 1);
double x = data(0), y = data(1), z = data(2);
double a = 6378137.0, b = 6356752.3142;
double e = sqrt(1 - (b / a) * (b / a));
double r = sqrt(x * x + y * y);
double E2 = a * a - b * b;
double F = 54 * b * b * z * z;
double G = r * r + (1 - e * e) * z * z - e * e * E2;
double c = (e * e * e * e * F * r * r) / pow(G, 3);
double s = pow(1 + c + sqrt(c * c + 2 * c), 1.0 / 3.0);
double P = F / (3 * pow(s + 1 / s + 1, 2) * G * G);
double Q = sqrt(1 + 2 * e * e * e * e * P);
double ro = -(P * e * e * r) / (1 + Q) + sqrt(0.5 * a * a * (1 + 1 / Q) - P * (1 - e * e) * z * z / (Q * (1 + Q)) - 0.5 * P * r * r);
double tmp = pow(r - e * e * ro, 2);
double U = sqrt(tmp + z * z);
double V = sqrt(tmp + (1 - e * e) * z * z);
double zo = (b * b * z) / (a * V);
double height = U * (1 - b * b / (a * V));
double lat = atan((z + e * e * zo) / r);
double lon = atan2(y, x);
llh << lon * 180 / M_PI, lat * 180 / M_PI, height;
return llh;
/**************for test purpose*************************
Eigen::MatrixXd ecef;
ecef.resize(3, 1);
Eigen::MatrixXd llh;
llh.resize(3, 1);
ecef(0) = -2418080.9387265667;
ecef(1) = 5386190.3905763263;
ecef(2) = 2405041.9305451373;
llh = ecef2llh(ecef);
cout << "llh ->: " << llh << "\n";
*/
}
1.4 当地水平坐标系(L 系)
- 定义:原点位于载体质心,X 轴指向东(E),Y 轴指向北(N),Z 轴指向天(U),构成 ENU 坐标系。
- 特性:与地球表面局部区域固联,适用于载体的相对位置描述。
1.5 导航坐标系(n 系)
- 定义:惯性导航算法的核心参考系,可选取 e 系或 L 系作为 n 系:
- e 系导航:直接输出地心地固坐标,便于与 GNSS 数据融合,模型简单但物理意义不直观;
- L 系导航:采用 NED 坐标系,物理意义明确,利于误差分析但模型复杂。
- 应用场景:组合导航解算优先选用 e 系,理论分析优先选用 L 系。
- 示意图:



1.6 载体坐标系(b 系)
- 定义:与载体固联的坐标系,原点位于惯导硬件中心,Z 轴朝上,Y 轴指向载体前进方向,X 轴指向前进方向右侧。
- 特性:惯性器件(加速度计、陀螺仪)的测量数据均基于 b 系输出。
- 示意图:



1.7 平台坐标系(p 系)
- 定义:平台式惯导中通过物理平台维持的水平指北坐标系,捷联惯导中由姿态矩阵模拟实现。
- 特性:受误差影响,p 系与真实 L 系存在失准角,需通过算法校正。
- 示意图:



1.8 计算机坐标系(c 系)
- 定义:由惯导解算的含误差经纬度确定的当地坐标系,用于误差模型推导。
- 特性:无实际物理意义,仅为理论分析中的辅助坐标系。
二、坐标系旋转描述方法
描述坐标系间旋转关系的常用工具包括欧拉角、旋转矩阵、四元数与旋转矢量,其中欧拉角与旋转矩阵的对应关系如下:
2.1 欧拉角旋转顺序
采用 Z→X→Y 旋转顺序:
- 绕 Z 轴旋转(航向角 Yaw,ψ):对应载体水平旋转;
- 绕 X 轴旋转(俯仰角 Pitch,θ):对应载体前后倾斜;
- 绕 Y 轴旋转(翻滚角 Roll,φ):对应载体左右倾斜。
- 示意图:

2.2 单轴旋转矩阵
- 绕 Z 轴旋转矩阵:

(注:原示意图中包含航向角ψ符号,矩阵形式为: R Z ( ψ ) = [ cos ψ − sin ψ 0 sin ψ cos ψ 0 0 0 1 ] R_Z(\psi) = \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} RZ(ψ)= cosψsinψ0−sinψcosψ0001 ) - 绕 X 轴旋转矩阵:
R X ( θ ) = [ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] R_X(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} RX(θ)= 1000cosθsinθ0−sinθcosθ - 绕 Y 轴旋转矩阵:
R Y ( ϕ ) = [ cos ϕ 0 sin ϕ 0 1 0 − sin ϕ 0 cos ϕ ] R_Y(\phi) = \begin{bmatrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{bmatrix} RY(ϕ)= cosϕ0−sinϕ010sinϕ0cosϕ
2.3 欧拉角值域
- 航向角ψ:
 (即[-π, π])
(即[-π, π]) - 俯仰角θ:
 (即[-π/2, π/2])
(即[-π/2, π/2]) - 翻滚角φ:[-π, π]
三、坐标系转换程序实现
3.1 ECEF 与 ENU 坐标系转换
Eigen::MatrixXd ecef2enu(Eigen::MatrixXd originllh, Eigen::MatrixXd ecef) // ECEF 转 ENU
{
double pi = M_PI;
double DEG2RAD = pi / 180.0;
double RAD2DEG = 180.0 / pi;
Eigen::MatrixXd enu(3, 1);
Eigen::MatrixXd oxyz = llh2ecef(originllh);
double ox = oxyz(0), oy = oxyz(1), oz = oxyz(2);
double dx = ecef(0) - ox, dy = ecef(1) - oy, dz = ecef(2) - oz;
double lon = originllh(0) * DEG2RAD;
double lat = originllh(1) * DEG2RAD;
enu(0) = -sin(lon) * dx + cos(lon) * dy;
enu(1) = -sin(lat) * cos(lon) * dx - sin(lat) * sin(lon) * dy + cos(lat) * dz;
enu(2) = cos(lat) * cos(lon) * dx + cos(lat) * sin(lon) * dy + sin(lat) * dz;
return enu;
/**************for test purpose*****suqare distance is about 37.4 meters********************
Eigen::MatrixXd llh; //original
llh.resize(3, 1);
llh(0) = 114.1775072541416;
llh(1) = 22.29817969722738;
llh(2) = 58;
Eigen::MatrixXd ecef;
ecef.resize(3, 1);
ecef(0) = -2418080.9387265667;
ecef(1) = 5386190.3905763263;
ecef(2) = 2405041.9305451373;
Eigen::MatrixXd enu;
enu.resize(3, 1);
enu = ecef2enu(llh, ecef);
cout << "enu ->: " << enu << "\n";
*/
}
Eigen::MatrixXd enu2ecef(Eigen::MatrixXd originllh, Eigen::MatrixXd enu) // ENU 转 ECEF
{
double e = enu(0), n = enu(1), u = enu(2);
double lon = originllh(0) * M_PI / 180.0;
double lat = originllh(1) * M_PI / 180.0;
Eigen::MatrixXd oxyz = llh2ecef(originllh);
double ox = oxyz(0), oy = oxyz(1), oz = oxyz(2);
oxyz(0) = ox - sin(lon) * e - cos(lon) * sin(lat) * n + cos(lon) * cos(lat) * u;
oxyz(1) = oy + cos(lon) * e - sin(lon) * sin(lat) * n + cos(lat) * sin(lon) * u;
oxyz(2) = oz + cos(lat) * n + sin(lat) * u;
return oxyz;
}
参考资料
大地坐标系 (WGS-84)、地心地固坐标系 (ECEF) 与东北天坐标系 (ENU) 的相互转换 C 语言代码分享 (链接已沉寂)
惯性导航原理(1):导航坐标系及相互转换
Mua111 于 2022-06-24 17:51:46 修改
一、导航坐标系转换说明
本文作者为导航专业从业者,工作方向涉及惯导与组合导航。因专业知识存在遗忘,故通过系列文章记录相关内容,内容若存在偏差,欢迎指正。
补充说明:不同参考资料中经纬度、卯酉圈、子午圈符号存在差异(如部分资料用
L
L
L 表示纬度、
λ
\lambda
λ 表示经度,部分用
B
B
B 表示纬度、
L
L
L 表示经度),本文因参考资料较多且未单独编辑公式,符号存在混淆,已在文中添加注释说明。
二、坐标系定义
2.1 惯性坐标系(地心惯性坐标系,i 系)
- 标识: O − X i Y i Z i O - X_iY_iZ_i O−XiYiZi,角标以 i i i 表示。
- 原点与轴定义:
- 原点 O O O 为地球质心;
- O Z i OZ_i OZi 轴沿地球自转轴方向;
- O X i OX_i OXi 轴为地球公转黄道平面与赤道平面的交线;
- O Y i OY_i OYi 轴按右手坐标系规则确定。
- 核心特性:不与地球固联,不随地球自转而转动。
- 测量关联:IMU(加速度计、陀螺仪)测量载体相对于 i i i 系的运动。
- 示意图:

2.2 地球坐标系(地心地固坐标系,e 系)
- 标识: O − X e Y e Z e O - X_eY_eZ_e O−XeYeZe。
- 原点与轴定义:
- 原点 O O O 为地球质心;
- O X e OX_e OXe 轴延伸通过本初子午线(0° 经度)与赤道的交点;
- O Z e OZ_e OZe 轴延伸通过地球北极(与地球自转轴重合);
- O Y e OY_e OYe 轴与 O X e OX_e OXe、 O Z e OZ_e OZe 轴构成右手坐标系,穿过赤道与 90° 经度交点。
- 应用场景:导航中常用于描述载体相对于地球的位置,作为参考坐标系。
- 示意图:

2.3 WGS - 84 坐标系(blh 坐标系)
- 别名:经纬高坐标系(经度 longitude、纬度 latitude、高度 altitude,简称 LLA 坐标系)。
- 坐标系归属:地理坐标系的一种,GPS 系统采用该坐标系;中国常用北京 54、西安 80、China2000 等其他地理坐标系。
- 原点与轴定义:
- O X OX OX 轴指向国际时间服务机构(BIH)1984.0 定义的零子午面与协议地球极(CTP)赤道的交点;
- O Z OZ OZ 轴指向 CTP 方向;
- O Y OY OY 轴与 O X OX OX、 O Z OZ OZ 轴构成右手坐标系。
- 参数定义:
- 大地纬度:过用户点 P P P 的基准椭球面法线与赤道面的夹角,取值范围 [ − 9 0 ∘ , + 9 0 ∘ ] [-90^\circ, +90^\circ] [−90∘,+90∘],北半球为正,南半球为负;
- 大地经度:过用户点 P P P 的子午面与本初子午线的夹角,取值范围 [ − 18 0 ∘ , + 18 0 ∘ ] [-180^\circ, +180^\circ] [−180∘,+180∘];
- 大地高度 h h h:过用户点 P P P 到基准椭球面的法线距离,基准椭球面以内为负,以外为正。
- 示意图:

2.4 当地水平地理坐标系(g 系)
- 常用类型:东北天(ENU)坐标系、北东地(NED)坐标系。
- 东北天(ENU)坐标系定义:
- 原点为载体所在点 P P P;
- Z Z Z 轴沿 P P P 点法线指向天顶(正方向);
- Y Y Y 轴沿 P P P 点子午线方向指向北(正方向);
- X X X 轴与 Y Z YZ YZ 平面垂直,指向东(正方向),构成右手坐标系。
- 北东地(NED)坐标系定义:
- 原点为载体所在点 P P P;
- X X X 轴沿 P P P 点子午线方向指向北(正方向);
- Y Y Y 轴与 X X X 轴垂直,指向东(正方向);
- Z Z Z 轴与 X Y XY XY 平面垂直,指向地(正方向),构成右手坐标系。
- 示意图:

2.5 平台坐标系(p 系)
- 定义:与平台式惯导系统中物理平台固联,描述平台指向的坐标系;若平台无误差且指向准确,称为理想平台坐标系。
- 应用说明:本文聚焦捷联惯导,后续内容不再涉及该坐标系。
- 示意图:

2.6 导航坐标系(n 系)
- 定位:惯性导航算法的基础参考系,载体的位置、速度、姿态解算均在该坐标系内完成。
- 选取方式:
- 选取地心地固坐标系(e 系):可直接输出 e 系下导航参数,便于与 GNSS 等大地测量手段融合;
- 选取当地水平地理坐标系(g 系):物理意义直观,是惯性导航中常用的导航系选择。
- 特性:仅为算法层面的 “虚拟” 坐标系,无实体对应。
2.7 载体坐标系(b 系)
- 定义:与载体固联,随载体运动而同步运动,原点与载体质心重合。
- 两种常用子类型:
- 右 - 前 - 上坐标系(对应东北天 g 系):
- X X X 轴沿载体横轴线指向右;
- Y Y Y 轴沿载体纵轴线指向前;
- Z Z Z 轴沿载体竖轴线向上,与 X X X、 Y Y Y 轴构成右手坐标系。
- 前 - 右 - 下坐标系(对应北东地 g 系):
- X X X 轴沿载体纵轴线指向前;
- Y Y Y 轴沿载体横轴线指向右;
- Z Z Z 轴沿载体竖轴线向下,与 X X X、 Y Y Y 轴构成右手坐标系。
- 右 - 前 - 上坐标系(对应东北天 g 系):
- 示意图:

三、坐标系间的相对转换关系
3.1 惯性坐标系(i 系)与地心地固坐标系(e 系)转换
- 转换基础:两坐标系原点重合,存在相对旋转;地球自转角速度(e 系相对于 i 系) ω i e = 7.292115 × 1 0 − 5 rad/s \omega_{ie} = 7.292115 \times 10^{-5}\ \text {rad/s} ωie=7.292115×10−5 rad/s,旋转方向自西向东,角速度矢量沿 Z Z Z 轴。
- i 系到 e 系的转换矩阵:

- e 系到 i 系的转换矩阵:因方向余弦矩阵为正交矩阵,其逆矩阵等于转置矩阵,故 C e i = C i e T C_{ei} = C_{ie}^T Cei=CieT( C i e C_{ie} Cie 为 i 系到 e 系转换矩阵, C e i C_{ei} Cei 为 e 系到 i 系转换矩阵)。
3.2 WGS - 84 坐标系(blh 系)与地心地固坐标系(e 系)转换
3.2.1 关键参数定义
- 子午圈曲率半径 R m R_m Rm:过载体点 P P P 且包含地球自转轴的平面(子午面)与椭球面交线的曲率半径。
- 卯酉圈曲率半径 R n R_n Rn:过载体点 P P P 且垂直于子午面的平面与椭球面交线的曲率半径。
- 参数计算公式(基于 WGS - 84 椭球模型):

其中, a = 6378137 m a = 6378137\ \text {m} a=6378137 m(地球椭球长半轴), e = 0.0818191908426 e = 0.0818191908426 e=0.0818191908426(第一偏心率), f = 1 / 298.257223563 f = 1/298.257223563 f=1/298.257223563(第一扁率), B B B 为大地纬度。 - 示意图:

3.2.2 具体转换公式
- blh 系到 e 系转换矩阵:

式中, N = R n N = R_n N=Rn(卯酉圈曲率半径), h h h 为大地高度, L L L 为大地经度, b = a ( 1 − f ) b = a (1 - f) b=a(1−f)(地球椭球短半轴)。 - e 系到 blh 系转换矩阵:

3.3 地心地固坐标系(e 系)与当地水平地理坐标系(g 系)转换
两坐标系转换通过位置矩阵(方向余弦阵)实现,具体形式随 g 系类型不同而变化。
3.3.1 g 系为东北天(ENU)坐标系
- 旋转步骤:
- g 系绕自身 Z Z Z 轴旋转 − π / 2 -\pi/2 −π/2;
- 绕旋转后 Y Y Y 轴旋转 − ( π / 2 − B ) -(\pi/2 - B) −(π/2−B)( B B B 为大地纬度,弧度制);
- 绕旋转后 Z Z Z 轴旋转 − L -L −L( L L L 为大地经度,弧度制),最终与 e 系坐标轴平行。
- e 系到 g 系转换矩阵:

- g 系到 e 系转换矩阵: C g e = C e g T C_{ge} = C_{eg}^T Cge=CegT( C e g C_{eg} Ceg 为 e 系到 g 系转换矩阵, C g e C_{ge} Cge 为 g 系到 e 系转换矩阵)。
- 旋转步骤示意图:

3.3.2 g 系为北东地(NED)坐标系
- e 系到 g 系转换矩阵:因常将 g 系作为导航系(n 系),故矩阵也可表示为
C
e
n
C_{en}
Cen(e 系到 n 系):

- g 系到 e 系转换矩阵: C g e = C e g T C_{ge} = C_{eg}^T Cge=CegT(或 C n e = C e n T C_{ne} = C_{en}^T Cne=CenT)。
3.4 当地水平地理坐标系(g/n 系)与载体坐标系(b 系)转换
转换基于欧拉角描述,具体形式随 g/n 系与 b 系的类型组合不同而变化。
3.4.1 组合 1:g/n 系为东北天(ENU)、b 系为右 - 前 - 上
- 欧拉角定义:

其中, ψ \psi ψ 为航向角, θ \theta θ 为俯仰角, ϕ \phi ϕ 为横滚角。 - 旋转顺序:
Z
Z
Z 轴(航向角)
→
X
\rightarrow X
→X 轴(俯仰角)
→
Y
\rightarrow Y
→Y 轴(横滚角):
- 绕 g 系 Z Z Z 轴旋转 − ψ -\psi −ψ;
- 绕旋转后 X X X 轴旋转 θ \theta θ;
- 绕旋转后 Y Y Y 轴旋转 ϕ \phi ϕ。
- 旋转矩阵(g 系到 b 系):

- 姿态矩阵(b 系到 g/n 系):
C
b
g
=
C
g
b
T
C_{bg} = C_{gb}^T
Cbg=CgbT(
C
g
b
C_{gb}
Cgb 为 g 系到 b 系旋转矩阵),具体形式:

- 符号规则:
- 俯仰角、横滚角:绕轴正转时姿态角为正,反转时为负;
- 航向角:绕轴反转时姿态角为正(因航向角定义为 Y Y Y 轴指北时为 0 0 0,北偏东顺时针递增,需 Z Z Z 轴反转实现)。
3.4.2 组合 2:g/n 系为北东地(NED)、b 系为前 - 右 - 下
- 欧拉角旋转顺序:
Z
Z
Z 轴(航向角)
→
Y
\rightarrow Y
→Y 轴(俯仰角)
→
X
\rightarrow X
→X 轴(横滚角):
- 绕 g 系 Z Z Z 轴旋转 ψ \psi ψ;
- 绕旋转后 Y Y Y 轴旋转 θ \theta θ;
- 绕旋转后 X X X 轴旋转 ϕ \phi ϕ。
- 旋转矩阵(g 系到 b 系):

- 展开后旋转矩阵:

- 符号规则:
- 俯仰角、横滚角:绕轴正转时姿态角为正,反转时为负;
- 航向角:绕轴正转时姿态角为正(因航向角定义为 X X X 轴指北时为 0 0 0,北偏东顺时针递增,与 Z Z Z 轴正转方向一致)。
- 示意图:

四、注意事项
不同坐标系组合下,欧拉角的旋转顺序与符号定义存在差异,是导航解算中误差的重要来源,需严格按照所选坐标系类型匹配对应转换规则,避免混淆。
惯性导航原理(2):导航基础知识
Mua111 于 2022-06-26 12:34:10 发布
本文系统阐述导航领域的基础理论知识,涵盖向量叉乘与反对称阵、欧拉角、坐标转换矩阵、四元数及等效旋转矢量的定义与相互转换关系。欧拉角存在万向节死锁问题,四元数与坐标转换矩阵作为替代方案各具优劣。此外,还详细介绍地球形状、地心纬度、重力模型等相关内容,为惯导解算及多传感器组合导航学习奠定基础。
一、矩阵基础知识
1.1 向量叉乘与反对称阵
设两个三维列向量分别为 V 1 = [ V 1 x , V 1 y , V 1 z ] T \boldsymbol{V}_1 = [V_{1x}, V_{1y}, V_{1z}]^T V1=[V1x,V1y,V1z]T 和 V 2 = [ V 2 x , V 2 y , V 2 z ] T \boldsymbol{V}_2 = [V_{2x}, V_{2y}, V_{2z}]^T V2=[V2x,V2y,V2z]T,二者叉乘(外积)可通过行列式规则表示为:

其中 i , j , k \boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k} i,j,k 分别为直角坐标系三个坐标轴方向的单位向量。
展开后形式为:

由此可定义反对称阵符号:

( V × ) \boldsymbol{(V \times)} (V×) 为三维向量 V \boldsymbol{V} V 对应的反对称阵,当 V \boldsymbol{V} V 为实向量时,满足 ( V × ) H = ( V × ) T = − ( V × ) \boldsymbol{(V \times)}^H = \boldsymbol{(V \times)}^T = -\boldsymbol{(V \times)} (V×)H=(V×)T=−(V×)(其中 H H H 表示共轭转置)。引入反对称阵后,两向量叉乘可等价表示为矩阵乘法运算: V 1 × V 2 = ( V 1 × ) V 2 \boldsymbol{V}_1 \times \boldsymbol{V}_2 = \boldsymbol{(V_1 \times)} \boldsymbol{V}_2 V1×V2=(V1×)V2。此外,反对称阵属于正规矩阵,满足 ( V × ) H ( V × ) = ( V × ) ( V × ) H \boldsymbol{(V \times)}^H \boldsymbol{(V \times)} = \boldsymbol{(V \times)} \boldsymbol{(V \times)}^H (V×)H(V×)=(V×)(V×)H。
二、欧拉角、坐标转换矩阵、四元数与等效旋转矢量
2.1 欧拉角
三维空间中物体具有六个自由度,包括沿 X , Y , Z X, Y, Z X,Y,Z 轴的平移和绕 X , Y , Z X, Y, Z X,Y,Z 轴的旋转。惯性导航中,通常采用偏航角(yaw)、俯仰角(pitch)、横滚角(roll)描述旋转运动,对应载体坐标系(前-右-下坐标系)的 Z , Y , X Z, Y, X Z,Y,X 轴(右-前-上坐标系对应 Z , X , Y Z, X, Y Z,X,Y 轴)。
2.1.1 旋转顺序
旋转顺序指绕坐标轴的转动先后顺序,如 X − Y − Z X-Y-Z X−Y−Z、 Y − X − Z Y-X-Z Y−X−Z 等,共有 ( x − y − z , y − z − x , z − x − y , x − z − y , z − y − x , y − x − z ) (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z) (x−y−z,y−z−x,z−x−y,x−z−y,z−y−x,y−x−z) 六种组合。由于旋转运算不满足交换律(如先绕 Z Z Z 轴转 3 0 ∘ 30^\circ 30∘ 再绕 Y Y Y 轴转 1 0 ∘ 10^\circ 10∘,与先绕 Y Y Y 轴转 1 0 ∘ 10^\circ 10∘ 再绕 Z Z Z 轴转 3 0 ∘ 30^\circ 30∘ 结果不同),必须明确旋转顺序才能唯一确定姿态。
2.1.2 内旋与外旋
-
内旋:绕坐标系自身的旋转轴转动(惯性导航解算中普遍采用);
-
外旋:绕参考坐标系(世界坐标系)固定的旋转轴转动。

注:导航领域中,导航系或当地地理坐标系到载体系的坐标旋转矩阵中,绕 Y Y Y 轴的旋转矩阵与绕 X , Z X, Z X,Z 轴的形式不同。这是因为绕 X , Z X, Z X,Z 轴旋转对应在 y o z , x o y yoz, xoy yoz,xoy 平面顺时针转动,而绕 Y Y Y 轴旋转对应在 z o x zox zox 平面顺时针转动( Z Z Z 轴为横轴, X X X 轴为纵轴),可通过右手坐标系规则验证。
2.1.3 优缺点与万向节死锁
-
优点:用三个变量直接对应三个旋转自由度,无冗余信息,物理意义直观;
-
缺点:存在万向节死锁问题,无法直接进行旋转叠加运算(需借助旋转矩阵),插值误差较大(四元数更适用于插值场景)。
万向节死锁原理:以 X − Y − Z X-Y-Z X−Y−Z 旋转顺序为例,若俯仰角(绕 Y Y Y 轴)旋转 9 0 ∘ 90^\circ 90∘,则 Z Z Z 轴会与旋转前 X X X 轴的反方向重合,此时绕 Z Z Z 轴的旋转与绕 X X X 轴的旋转效果等价,导致丢失一个自由度。从矩阵角度分析,当 Y Y Y 轴旋转角度为 9 0 ∘ 90^\circ 90∘ 时,旋转矩阵为:
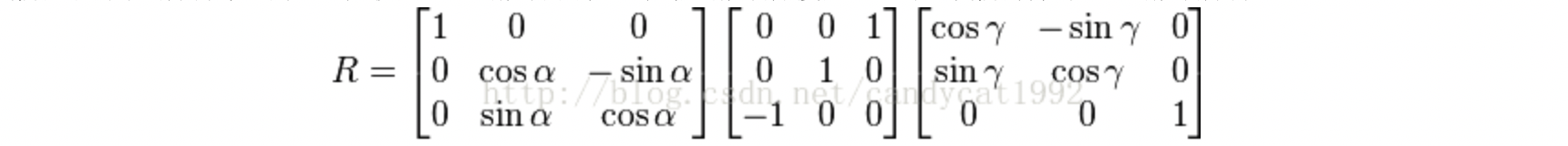
左乘该矩阵后可得:

可见,改变第一次(绕 X X X 轴)和第三次(绕 Z Z Z 轴)的旋转角度,矩阵第一行和第三列数值不变,最终姿态无法唯一确定,即出现万向节死锁。
2.2 坐标转换矩阵
坐标转换矩阵是表示旋转变换的 3 阶正交矩阵,其行列式值恒为 1,自由度为 3(与旋转运动的自由度一致)。
2.2.1 优缺点
-
优点:同一姿态对应的旋转矩阵唯一(无欧拉角的多义性),可通过矩阵乘法实现连续旋转的叠加运算,对坐标转换运算友好;
-
缺点:用 9 个元素描述 3 个自由度,存在冗余信息。
2.3 四元数
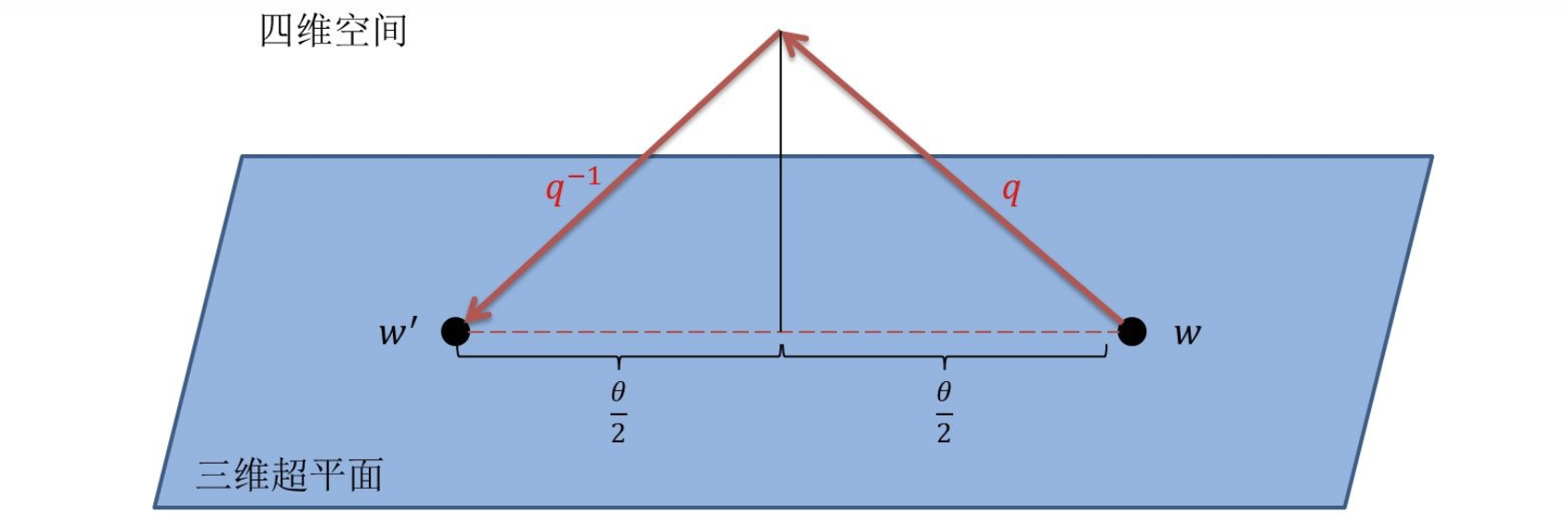
为解决欧拉角的万向节死锁问题和旋转矩阵的冗余问题,引入四元数表示旋转。四元数是由四个元素组成的超复数,形式为 q = ( q 0 , q 1 , q 2 , q 3 ) \boldsymbol{q} = (q_0, q_1, q_2, q_3) q=(q0,q1,q2,q3),其中 q 0 q_0 q0 为转动幅度的函数, q 1 , q 2 , q 3 q_1, q_2, q_3 q1,q2,q3 为旋转轴与转动幅度的函数。尽管四元数包含四个元素,但满足模值为 1 的约束( q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1 q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1 q02+q12+q22+q32=1),实际独立自由度仍为 3。
四元数的旋转运算规则为:
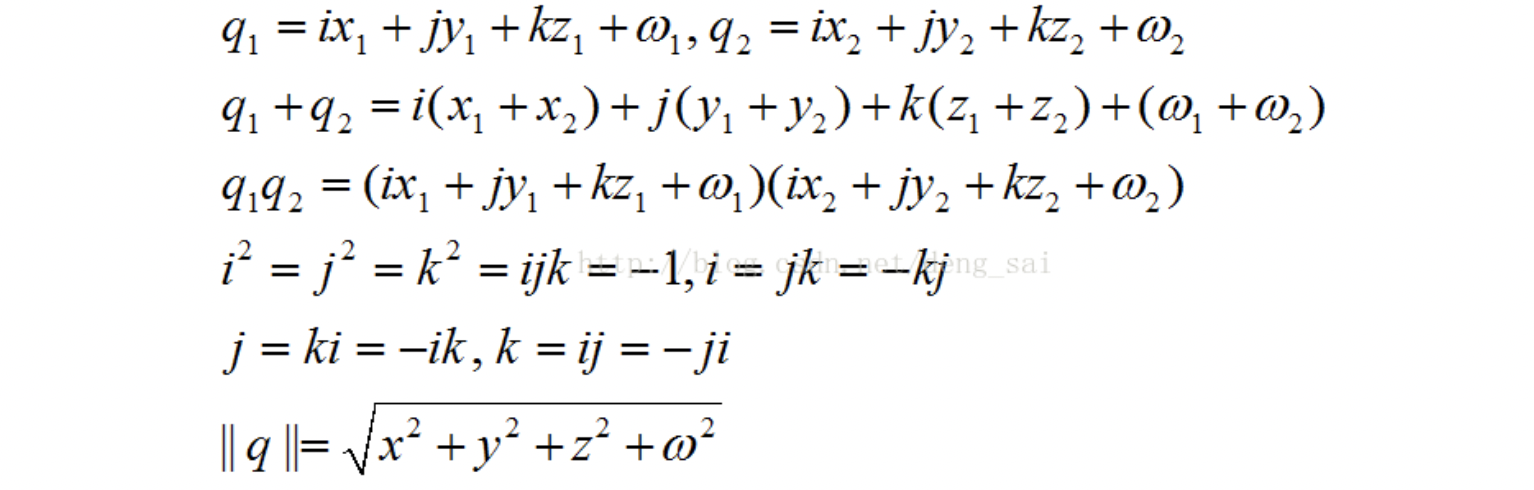

其中 q ∗ \boldsymbol{q}^* q∗ 为四元数 q \boldsymbol{q} q 的共轭, q v q ∗ \boldsymbol{q} \boldsymbol{v} \boldsymbol{q}^* qvq∗ 表示三维向量 v \boldsymbol{v} v 经四元数旋转后的结果(需通过共轭四元数二次旋转,确保结果仍为三维向量)。若仅用 q \boldsymbol{q} q 旋转一次,向量会被映射到四维空间(实部非零),无法保持三维特性,示意图如下:
四元数理论推导较为复杂,如需深入学习,可参考 Krasjet 撰写的《四元数与三维旋转》(链接:最详细的四元数讲解,保姆级教学 )。
2.4 轴角/旋转矢量
轴角表示法通过“旋转轴 + 旋转角”描述旋转,原始形式包含四个参数(旋转轴 u = [ x , y , z ] T \boldsymbol{u} = [x, y, z]^T u=[x,y,z]T + 旋转角 θ \theta θ),但旋转轴的模长无实际意义(仅需方向信息)。因此,通常规定旋转轴为单位向量( ∥ u ∥ = x 2 + y 2 + z 2 = 1 \|\boldsymbol{u}\| = \sqrt{x^2 + y^2 + z^2} = 1 ∥u∥=x2+y2+z2=1),此时独立自由度为 3(旋转轴方向 2 个自由度 + 旋转角 1 个自由度)。
旋转矢量与轴角本质一致,是将旋转角与单位旋转轴结合后的三维向量,形式为 r v = [ x ⋅ θ , y ⋅ θ , z ⋅ θ ] T \boldsymbol{r}_v = [x \cdot \theta, y \cdot \theta, z \cdot \theta]^T rv=[x⋅θ,y⋅θ,z⋅θ]T。
2.4.1 旋转矢量的推导
将向量 v \boldsymbol{v} v 分解为平行于旋转轴 u \boldsymbol{u} u 的分量 v ∥ \boldsymbol{v}_\parallel v∥ 和垂直于旋转轴的分量 v ⊥ \boldsymbol{v}_\perp v⊥:

其中, v ∥ \boldsymbol{v}_\parallel v∥ 为 v \boldsymbol{v} v 在 u \boldsymbol{u} u 上的正交投影,表达式为:

v ⊥ = v − v ∥ = v − ( u ⋅ v ) u \boldsymbol{v}_\perp = \boldsymbol{v} - \boldsymbol{v}_\parallel = \boldsymbol{v} - (\boldsymbol{u} \cdot \boldsymbol{v}) \boldsymbol{u} v⊥=v−v∥=v−(u⋅v)u,旋转过程中 v ∥ \boldsymbol{v}_\parallel v∥ 方向不变( v ∥ ′ = v ∥ \boldsymbol{v}_\parallel' = \boldsymbol{v}_\parallel v∥′=v∥),仅需考虑 v ⊥ \boldsymbol{v}_\perp v⊥ 的旋转。
构造同时正交于 u \boldsymbol{u} u 和 v ⊥ \boldsymbol{v}_\perp v⊥ 的向量 w = u × v ⊥ \boldsymbol{w} = \boldsymbol{u} \times \boldsymbol{v}_\perp w=u×v⊥(指向 v ⊥ \boldsymbol{v}_\perp v⊥ 逆时针旋转 9 0 ∘ 90^\circ 90∘ 的方向),则 v ⊥ \boldsymbol{v}_\perp v⊥ 旋转后的分量为:
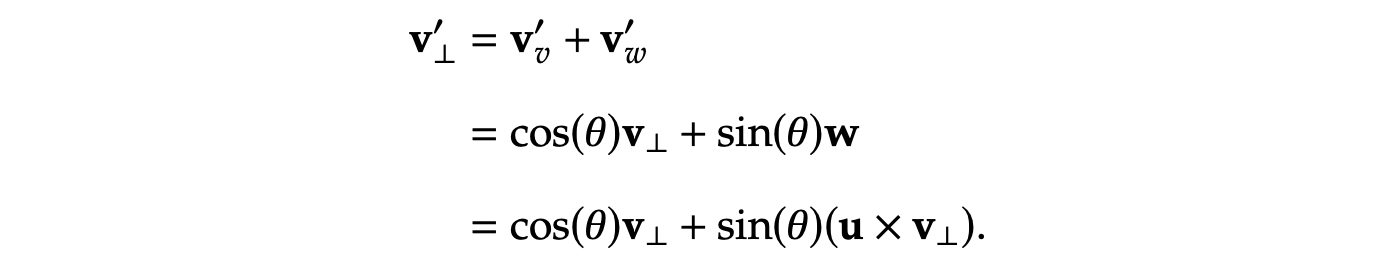
结合叉乘分配律:

最终得到向量 v \boldsymbol{v} v 绕单位轴 u \boldsymbol{u} u 旋转 θ \theta θ 角后的结果:
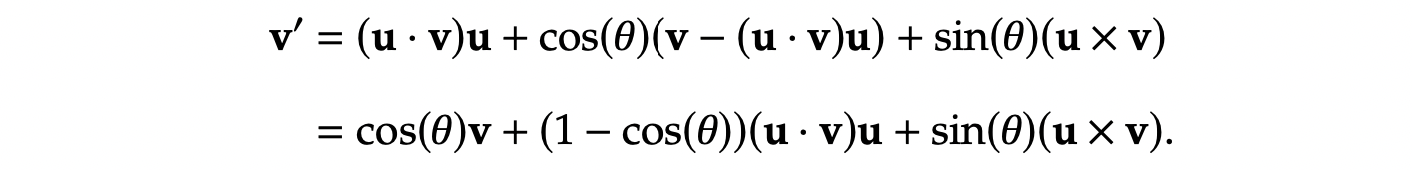
2.5 各旋转表示方法的相互转换
2.5.1 欧拉角 ↔ \leftrightarrow ↔ 坐标转换矩阵
设坐标系 1 相对于坐标系 2 的欧拉角(yaw, pitch, roll)为 α , β , γ \alpha, \beta, \gamma α,β,γ(北东地坐标系下),则坐标转换矩阵(坐标系 2 到坐标系 1)为:
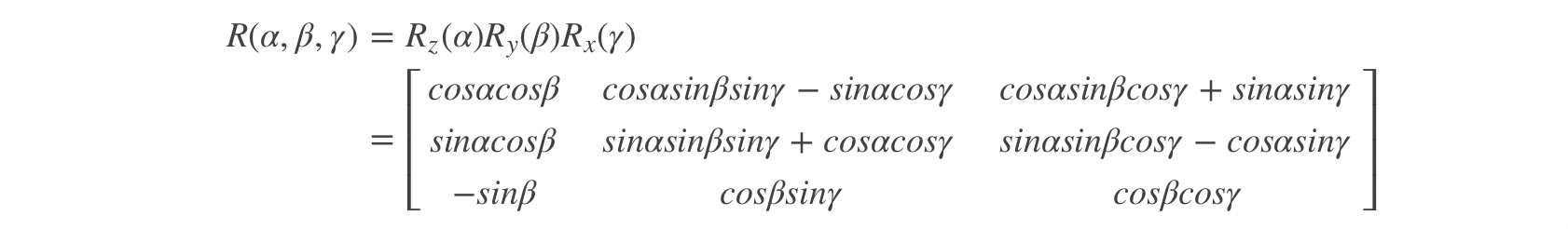
其中各单轴旋转矩阵为:
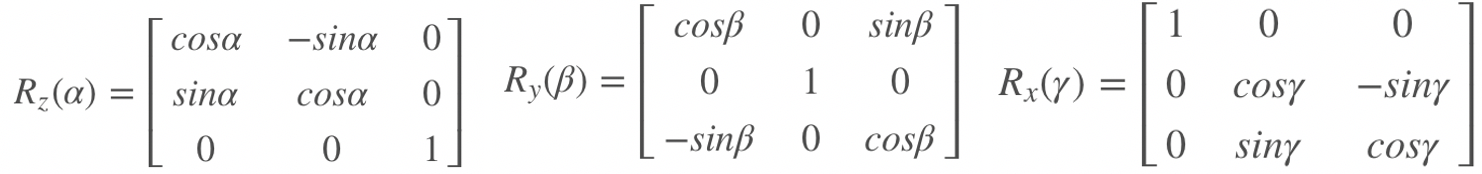
坐标转换矩阵到欧拉角的逆转换公式为:

2.5.2 欧拉角 ↔ \leftrightarrow ↔ 四元数
绕 Z − Y − X Z-Y-X Z−Y−X 轴旋转(欧拉角 yaw= ψ \psi ψ, pitch= θ \theta θ, roll= ϕ \phi ϕ)时,欧拉角到四元数的转换公式为:

四元数到欧拉角的逆转换公式为:
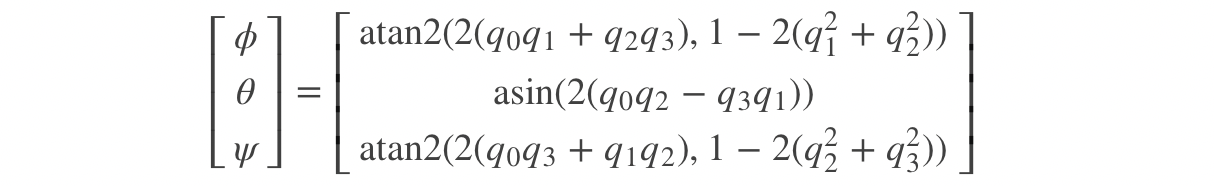
2.5.3 坐标转换矩阵 ↔ \leftrightarrow ↔ 四元数
四元数 q = ( q 0 , q 1 , q 2 , q 3 ) \boldsymbol{q} = (q_0, q_1, q_2, q_3) q=(q0,q1,q2,q3) 对应的坐标转换矩阵为:
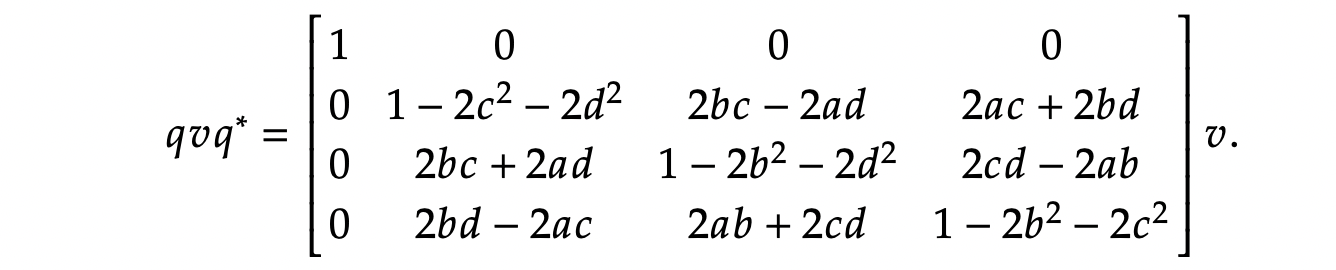
等价形式(基于旋转轴 u = [ u x , u y , u z ] T \boldsymbol{u} = [u_x, u_y, u_z]^T u=[ux,uy,uz]T 和旋转角 θ \theta θ,其中 q 0 = cos θ 2 , q 1 = u x sin θ 2 , q 2 = u y sin θ 2 , q 3 = u z sin θ 2 q_0 = \cos\frac{\theta}{2}, q_1 = u_x \sin\frac{\theta}{2}, q_2 = u_y \sin\frac{\theta}{2}, q_3 = u_z \sin\frac{\theta}{2} q0=cos2θ,q1=uxsin2θ,q2=uysin2θ,q3=uzsin2θ):
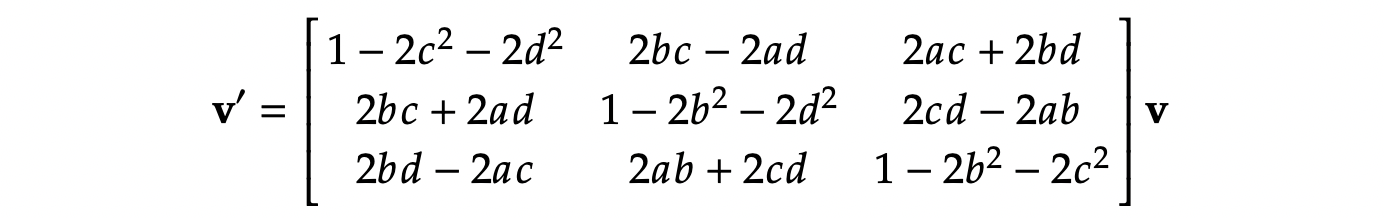

坐标转换矩阵 R \boldsymbol{R} R 到四元数的转换公式为:

2.5.4 坐标转换矩阵 ↔ \leftrightarrow ↔ 旋转矢量
根据罗德里格斯公式,旋转矢量 r v = θ u \boldsymbol{r}_v = \theta \boldsymbol{u} rv=θu( u \boldsymbol{u} u 为单位旋转轴)到坐标转换矩阵的转换公式为:

坐标转换矩阵 R \boldsymbol{R} R 到旋转矢量的转换公式为:
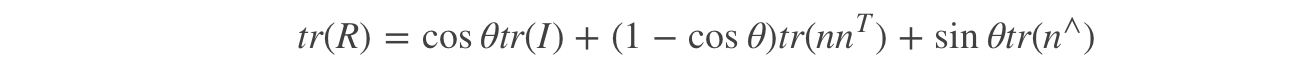
其中旋转角 θ = arccos ( tr ( R ) − 1 2 ) \theta = \arccos\left( \frac{\text{tr}(\boldsymbol{R}) - 1}{2} \right) θ=arccos(2tr(R)−1), tr ( R ) \text{tr}(\boldsymbol{R}) tr(R) 为矩阵 R \boldsymbol{R} R 的迹。
2.5.5 四元数 ↔ \leftrightarrow ↔ 旋转矢量
四元数 q = ( q 0 , q 1 , q 2 , q 3 ) \boldsymbol{q} = (q_0, q_1, q_2, q_3) q=(q0,q1,q2,q3) 到旋转矢量的转换公式为:
θ = 2 arccos ( q 0 ) , [ u x , u y , u z ] T = [ q 1 , q 2 , q 3 ] T / sin θ 2 \theta = 2\arccos(q_0),\quad [u_x, u_y, u_z]^T = [q_1, q_2, q_3]^T / \sin\frac{\theta}{2} θ=2arccos(q0),[ux,uy,uz]T=[q1,q2,q3]T/sin2θ
旋转矢量 r v = θ u \boldsymbol{r}_v = \theta \boldsymbol{u} rv=θu 到四元数的转换公式为:
q = ( cos θ 2 , u x sin θ 2 , u y sin θ 2 , u z sin θ 2 ) \boldsymbol{q} = \left( \cos\frac{\theta}{2}, u_x \sin\frac{\theta}{2}, u_y \sin\frac{\theta}{2}, u_z \sin\frac{\theta}{2} \right) q=(cos2θ,uxsin2θ,uysin2θ,uzsin2θ)
三、地球形状及重力模型
3.1 地球形状
3.1.1 地心纬度与地理纬度
-
地心纬度 φ \varphi φ:椭圆上某点 P P P 与地心 O e O_e Oe 的连线 P O e PO_e POe 与赤道面( O e X e O_eX_e OeXe 轴)的夹角,取值范围 [ − 9 0 ∘ , 9 0 ∘ ] [-90^\circ, 90^\circ] [−90∘,90∘],北纬为正,南纬为负;
-
地理纬度(简称纬度) L L L:过 P P P 点的椭圆法线 P Q PQ PQ 与赤道面的夹角,取值范围 [ − 9 0 ∘ , 9 0 ∘ ] [-90^\circ, 90^\circ] [−90∘,90∘];
-
地心垂线: P O e PO_e POe 对应的方向;地理垂线: P Q PQ PQ 对应的方向。

设地球椭球长半轴为 R e R_e Re,短半轴为 R n R_n Rn,则:
-
椭圆扁率(椭圆度) f f f:

-
椭圆偏心率 e e e:
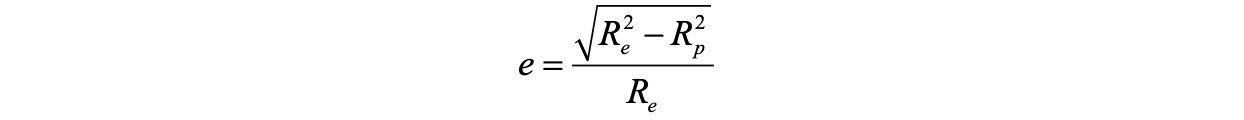
-
扁率与偏心率的换算关系:

3.1.2 大地坐标与位置矩阵
大地坐标(地理坐标)用于描述点相对于地球椭球的空间位置,记为 O g ( λ , L , h ) O_g(\lambda, L, h) Og(λ,L,h),其中 λ \lambda λ 为经度, L L L 为纬度, h h h 为椭球高度(过 O g O_g Og 点的法线到椭球面的距离)。
以椭球表面 P P P 点为原点建立坐标系 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0(纬圈切线指东为 X 0 X_0 X0 轴,经圈切线指北为 Y 0 Y_0 Y0 轴,椭球面法线指天为 Z 0 Z_0 Z0 轴),将原点沿 Z 0 Z_0 Z0 轴平移 h h h 得到当地地理坐标系 O g X g Y g Z g O_gX_gY_gZ_g OgXgYgZg(三轴分别平行于 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0 的同名坐标轴)。

设 O g O_g Og 点在当地地理坐标系中的速度为 v e g g = [ v x , v y , v z ] T \boldsymbol{v}_{e_g}^g = [v_x, v_y, v_z]^T vegg=[vx,vy,vz]T(东北天坐标系: v x v_x vx 为东向速度, v y v_y vy 为北向速度, v z v_z vz 为天向速度),则速度与大地坐标的关系为:



综合可得:

注:若采用北东地坐标系,需将东向速度与北向速度互换,地向速度前加负号。
3.2 重力模型
重力是地球万有引力与离心力的合力,即 g = F + F ′ \boldsymbol{g} = \boldsymbol{F} + \boldsymbol{F}' g=F+F′,其中 F \boldsymbol{F} F 为引力矢量, F ′ \boldsymbol{F}' F′ 为离心力矢量。

3.2.1 圆球假设下的重力公式
若地球为密度均匀的圆球体,引力指向地心,根据牛顿万有引力定律,地球对表面或外部单位质点的引力大小为:

其中 G G G 为万有引力常数, M M M 为地球质量, r r r 为质点到地心的距离。
地球自转角速率为 ω i e \omega_{ie} ωie,表面单位质点受到的离心力大小为:

其中 R R R 为地球半径, L L L 为地理纬度(圆球假设中与地心纬度一致)。
引力与离心力的夹角为 π − L \pi - L π−L,根据余弦定理,纬度 L L L 处的重力大小为:

其中 g e = F − ω i e 2 R g_e = F - \omega_{ie}^2 R ge=F−ωie2R 为赤道上的重力大小。
3.2.2 椭球假设下的重力公式
圆球假设与实际地球形状偏差较大,实测精度不足,旋转椭球假设下的地球重力公式为:

惯性导航原理(3):姿态微分方程及初始对准
Mua111 于 2022-06-26 18:27:12 发布
本文系统介绍姿态微分方程的三种表达形式(欧拉角、方向余弦阵、四元数)及其在不同坐标系下的应用,同时阐述惯性导航系统的粗对准过程,包括北东地坐标系下的解析粗对准与罗经粗对准方法,强调粗对准对陀螺敏感地球自转的要求。文中未深入展开姿态微分方程的求解过程,但提供了关键公式与核心原理,为后续惯导解算学习奠定基础。
一、姿态微分方程及初始对准
本章知识点相较于前两章更为聚焦,是进入惯性导航解算阶段的核心过渡内容。
二、姿态微分方程
2.1 欧拉角微分方程
当导航坐标系为东北天坐标系、IMU 载体坐标系为右前上坐标系时,欧拉角旋转顺序定义为 Z→X→Y(依次对应偏航角 yaw、俯仰角 pitch、滚转角 roll)。

其中, C ψ \boldsymbol{C}_\psi Cψ 为绕 Z 轴的旋转矩阵, C θ \boldsymbol{C}_\theta Cθ 为绕 X 轴的旋转矩阵, C ϕ \boldsymbol{C}_\phi Cϕ 为绕 Y 轴的旋转矩阵; C n b \boldsymbol{C}_n^b Cnb 表示导航系到载体系的坐标转换矩阵, X b \boldsymbol{X}_b Xb 为载体坐标系下的向量, X n \boldsymbol{X}_n Xn 为导航坐标系下的向量,满足坐标转换关系:
X n = C n b ⋅ X b \boldsymbol{X}_n = \boldsymbol{C}_n^b \cdot \boldsymbol{X}_b Xn=Cnb⋅Xb
2.1.1 角速度分解与推导
-
绕 Y 轴(滚转角)的角速度
假设已完成绕 Z、X、Y 三轴的全部旋转,此时绕 Y 轴的角速度在载体系与导航系中一致,表达式为:
ω b ( roll ) = [ d ( pitch ) d t , 0 , 0 ] T \boldsymbol{\omega}_b(\text{roll}) = \left[ \frac{d(\text{pitch})}{dt}, 0, 0 \right]^T ωb(roll)=[dtd(pitch),0,0]T
-
绕 X 轴(俯仰角)的角速度
假设已完成绕 Z、X 轴的旋转,未完成绕 Y 轴的旋转,此时绕 X 轴的角速度需通过 C ϕ \boldsymbol{C}_\phi Cϕ 转换至载体系,表达式为:
ω b ( pitch ) = C ϕ ⋅ [ 0 , d ( roll ) d t , 0 ] T \boldsymbol{\omega}_b(\text{pitch}) = \boldsymbol{C}_\phi \cdot \left[ 0, \frac{d(\text{roll})}{dt}, 0 \right]^T ωb(pitch)=Cϕ⋅[0,dtd(roll),0]T
-
绕 Z 轴(偏航角)的角速度
假设仅完成绕 Z 轴的旋转,未完成绕 X、Y 轴的旋转,此时绕 Z 轴的角速度需通过 C ϕ ⋅ C θ \boldsymbol{C}_\phi \cdot \boldsymbol{C}_\theta Cϕ⋅Cθ 转换至载体系,表达式为:
ω b ( yaw ) = C ϕ ⋅ C θ ⋅ [ 0 , 0 , d ( yaw ) d t ] T \boldsymbol{\omega}_b(\text{yaw}) = \boldsymbol{C}_\phi \cdot \boldsymbol{C}_\theta \cdot \left[ 0, 0, \frac{d(\text{yaw})}{dt} \right]^T ωb(yaw)=Cϕ⋅Cθ⋅[0,0,dtd(yaw)]T
2.1.2 欧拉角微分方程整合
综合上述三部分角速度,载体系相对于导航系的角速度 ω n b b = [ ω n b x b , ω n b y b , ω n b z b ] T \boldsymbol{\omega}_{nb}^b = \left[ \omega_{nbx}^b, \omega_{nby}^b, \omega_{nbz}^b \right]^T ωnbb=[ωnbxb,ωnbyb,ωnbzb]T 满足:
[ ω n b x b ω n b y b ω n b z b ] = [ d ( pitch ) d t 0 0 ] + C ϕ ⋅ [ 0 d ( roll ) d t 0 ] + C ϕ ⋅ C θ ⋅ [ 0 0 d ( yaw ) d t ] \begin{bmatrix} \omega_{nbx}^b \\ \omega_{nby}^b \\ \omega_{nbz}^b \end{bmatrix} = \begin{bmatrix} \frac{d(\text{pitch})}{dt} \\ 0 \\ 0 \end{bmatrix} + \boldsymbol{C}_\phi \cdot \begin{bmatrix} 0 \\ \frac{d(\text{roll})}{dt} \\ 0 \end{bmatrix} + \boldsymbol{C}_\phi \cdot \boldsymbol{C}_\theta \cdot \begin{bmatrix} 0 \\ 0 \\ \frac{d(\text{yaw})}{dt} \end{bmatrix} ωnbxbωnbybωnbzb = dtd(pitch)00 +Cϕ⋅ 0dtd(roll)0 +Cϕ⋅Cθ⋅ 00dtd(yaw)
整理后可得欧拉角微分方程。当导航坐标系为北东地坐标系、载体坐标系为前右下坐标系时,欧拉角微分方程具体形式为:


2.1.3 局限性说明
当俯仰角 θ = 9 0 ∘ \theta = 90^\circ θ=90∘ 时,欧拉角微分方程存在奇异性(无解),因此欧拉角方法不适用于全姿态飞行器(如无人机、航天器)的姿态描述。
2.2 方向余弦阵微分方程
方向余弦阵(坐标转换矩阵)的微分方程是描述姿态变化的核心方程,其推导基于刚体运动学原理,具体形式如下:


其中, [ Ω n b b ] \left[ \boldsymbol{\Omega}_{nb}^b \right] [Ωnbb] 为载体系相对于导航系角速度 ω n b b \boldsymbol{\omega}_{nb}^b ωnbb 对应的反对称阵,满足反对称阵的基本性质:
[ Ω n b b ] T = − [ Ω n b b ] \left[ \boldsymbol{\Omega}_{nb}^b \right]^T = -\left[ \boldsymbol{\Omega}_{nb}^b \right] [Ωnbb]T=−[Ωnbb]
反对称阵 [ Ω n b b ] \left[ \boldsymbol{\Omega}_{nb}^b \right] [Ωnbb] 的具体形式为:

2.3 四元数微分方程
设导航系(n 系)到载体系(b 系)的姿态四元数为 q = ( q 0 , q 1 , q 2 , q 3 ) \boldsymbol{q} = (q_0, q_1, q_2, q_3) q=(q0,q1,q2,q3)(其中 q 0 q_0 q0 为标量部分, q 1 , q 2 , q 3 q_1, q_2, q_3 q1,q2,q3 为矢量部分),则四元数的微分方程形式如下:


四元数微分方程的详细推导可参考文献:姿态四元数微分方程推导

需说明的是,姿态微分方程的求解涉及数值积分(如欧拉积分、龙格-库塔积分),过程较为复杂,本文仅列出微分方程的标准形式,后续章节将展开求解方法。
三、粗对准
惯性导航系统的对准是建立导航系与载体系姿态关系的过程,按不同分类标准可分为:动基座对准与静基座对准、自对准与传递对准、粗对准与精对准。其中,动基座对准需依赖外界参考信息(如速度、姿态、位置),精对准通常涉及卡尔曼滤波算法;本章仅介绍静基座条件下的粗对准方法,精对准内容将在后续章节展开。
重要前提:以下两种粗对准方法均要求陀螺能够敏感地球自转角速度 ω i e \omega_{ie} ωie(约 7.292 × 1 0 − 5 rad/s 7.292 \times 10^{-5}\ \text{rad/s} 7.292×10−5 rad/s),否则无法实现坐标系的初始定向。
3.1 北东地坐标系下的解析粗对准
解析粗对准基于静基座下的重力矢量与地球自转角速度矢量,通过矢量投影建立导航系与载体系的姿态关系,具体推导过程与公式如下:






3.2 北东地坐标系下的罗经粗对准
罗经粗对准模拟传统陀螺罗经的工作原理,分为水平调平与航向求解两个步骤,通过构建闭环控制实现姿态的初始对准。
3.2.1 水平调平
水平调平的核心是利用加速度计测量的重力矢量投影,消除载体系与导航系在水平方向(东向、北向)的姿态偏差,具体公式与控制逻辑如下:





3.2.2 航向求解
航向求解基于陀螺测量的地球自转角速度投影,通过计算东向角速度偏差确定载体的初始航向角,具体公式与推导过程如下:




3.2.3 其他粗对准方法补充
除解析粗对准与罗经粗对准外,常用的粗对准方法还包括双矢量定姿法、多矢量定姿法等。由于粗对准的后续流程通常衔接精对准(姿态偏差会通过滤波收敛),因此本章未展开上述方法的详细推导。
via:
-
坐标系转换详解-优快云 博客
https://blog.youkuaiyun.com/hxlove123456/article/details/83033387 -
常见导航坐标系定义_北天东坐标系-优快云 博客
https://blog.youkuaiyun.com/bltly/article/details/109177418 -
导航坐标系与姿态变换详解-优快云 博客
https://blog.youkuaiyun.com/barry_123/article/details/116501977 -
地图坐标系大全:常用地图坐标系详解与转换指南-优快云 博客
https://blog.youkuaiyun.com/weixin_39888010/article/details/129097344 -
惯性导航 惯性坐标系转换理解_角速度 b 系相对于 i 在 b 系里的投影 wibb 和 b 系相对于 n 在 b 系里的投影 wnbb 的关系-优快云 博客
https://blog.youkuaiyun.com/qq_53131867/article/details/140655219 -
常用导航坐标系 及 转换关系(理论+程序)-优快云 博客
https://blog.youkuaiyun.com/hltt3838/article/details/110433602 -
惯性导航原理(1):导航坐标系及相互转换_惯导坐标转换-优快云 博客
https://blog.youkuaiyun.com/Mua111/article/details/125433510 -
惯性导航原理(2):导航基础知识_惯导 原理-优快云 博客
https://blog.youkuaiyun.com/Mua111/article/details/125459185 -
惯性导航原理(3):姿态微分方程及初始对准_欧拉角微分方程-优快云 博客
https://blog.youkuaiyun.com/Mua111/article/details/125470317 -
经纬高坐标系转到东北天坐标系_经纬高转北天东坐标系-优快云 博客
https://blog.youkuaiyun.com/sdsfdsfdsds/article/details/109219416 -
北东地/东北天两种导航坐标系与姿态转换_北东地坐标系-优快云 博客
https://blog.youkuaiyun.com/zht2370201/article/details/89313370 -
无人导航常见坐标系 - Ethan_da - 博客园
https://www.cnblogs.com/ethanda/p/10325109.html





















 2461
2461

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








