注:本文为 “数学教育” 相关合辑。
英文引文,机翻未校。
如有内容异常,请看原文。
A Mathematician’s Lament
一位数学家的叹息
by Paul Lockhart
保罗·洛克哈特 著
A musician wakes from a terrible nightmare. In his dream he finds himself in a society where music education has been made mandatory. “We are helping our students become more competitive in an increasingly sound-filled world.” Educators, school systems, and the state are put in charge of this vital project. Studies are commissioned, committees are formed, and decisions are made- all without the advice or participation of a single working musician or composer.
一位音乐家从一场可怕的噩梦中惊醒。梦中,他置身于一个将音乐教育列为必修课的社会。“在这个日益充斥着声音的世界里,我们正在帮助学生提升竞争力。”教育工作者、学校系统和政府负责主导这一重要项目。相关研究纷纷启动,各类委员会相继成立,各项决策陆续出台——而这一切,却没有征求任何一位在职音乐家或作曲家的意见,也没有让他们参与其中。
Since musicians are known to set down their ideas in the form of sheet music, these curious black dots and lines must constitute the “language of music.” It is imperative that students become fluent in this language if they are to attain any degree of musical competence; indeed, it would be ludicrous to expect a child to sing a song or play an instrument without having a thorough grounding in music notation and theory. Playing and listening to music, let alone composing an original piece, are considered very advanced topics and are generally put off until college, and more often graduate school.
众所周知,音乐家会以乐谱的形式记录自己的想法,因此这些奇特的黑点和线条必然就是“音乐的语言”。学生若想在音乐方面达到一定的造诣,熟练掌握这门语言至关重要;事实上,若没有扎实的音乐记谱法和理论基础,就期望孩子能唱歌或演奏乐器,那简直是天方夜谭。演奏和聆听音乐,更不用说创作原创作品,都被视为非常高深的内容,通常要推迟到大学,甚至研究生阶段才会涉及。
As for the primary and secondary schools, their mission is to train students to use this language- to jiggle symbols around according to a fixed set of rules: “Music class is where we take out our staff paper, our teacher puts some notes on the board, and we copy them or transpose them into a different key. We have to make sure to get the clefs and key signatures right, and our teacher is very picky about making sure we fill in our quarter-notes completely. One time we had a chromatic scale problem and I did it right, but the teacher gave me no credit because I had the stems pointing the wrong way.”
而中小学的使命,则是训练学生使用这门语言——按照一套固定的规则摆弄这些符号:“音乐课上,我们拿出五线谱纸,老师在黑板上写下一些音符,我们要么抄写下来,要么转调到另一个调式。我们必须确保谱号和调号不出错,老师对四分音符的填写是否完整也格外挑剔。有一次我做半音阶的题目完全做对了,但老师却没给我分,就因为音符的符干方向错了。”
In their wisdom, educators soon realize that even very young children can be given this kind of musical instruction. In fact it is considered quite shameful if one’s third-grader hasn’t completely memorized his circle of fifths. “I’ll have to get my son a music tutor. He simply won’t apply himself to his music homework. He says it’s boring. He just sits there staring out the window, humming tunes to himself and making up silly songs.”
教育工作者们“英明地”很快意识到,即便非常年幼的孩子也能接受这种音乐教学。事实上,如果一个三年级学生还没有完全记住五度圈,会被认为是相当丢脸的事。“我得给儿子请个音乐家教了。他根本不认真做音乐作业,说太无聊了。他就坐在那儿盯着窗外,自己哼着调子,编些傻兮兮的歌。”
In the higher grades the pressure is really on. After all, the students must be prepared for the standardized tests and college admissions exams. Students must take courses in Scales and Modes, Meter, Harmony, and Counterpoint. “It’s a lot for them to learn, but later in college when they finally get to hear all this stuff, they’ll really appreciate all the work they did in high school.” Of course, not many students actually go on to concentrate in music, so only a few will ever get to hear the sounds that the black dots represent. Nevertheless, it is important that every member of society be able to recognize a modulation or a fugal passage, regardless of the fact that they will never hear one. “To tell you the truth, most students just aren’t very good at music. They are bored in class, their skills are terrible, and their homework is barely legible. Most of them couldn’t care less about how important music is in today’s world; they just want to take the minimum number of music courses and be done with it. I guess there are just music people and non-music people. I had this one kid, though, man was she sensational! Her sheets were impeccable- every note in the right place, perfect calligraphy, sharps, flats, just beautiful. She’s going to make one hell of a musician someday.”
到了高年级,压力就真的来了。毕竟,学生们必须为标准化考试和大学入学考试做准备。他们要学习音阶与调式、节拍、和声与对位法等课程。“要学的东西太多了,但等他们上了大学,终于能听到这些内容的实际音效时,就会真心感激高中时付出的努力。”当然,实际上并没有多少学生会继续主修音乐,所以只有少数人能真正听到这些黑点所代表的声音。尽管如此,社会中的每一个成员都应该能够识别转调或赋格段落,即便他们这辈子都不会听到这些东西,这一点依然很重要。“说实话,大多数学生其实并不擅长音乐。他们在课堂上感到无聊,技能糟糕透顶,作业写得难以辨认。他们大多根本不在乎音乐在当今世界有多重要,只是想修完最少的音乐课程,赶紧了事。我想,人大概分为有音乐天赋的和没有音乐天赋的吧。不过我曾遇到过一个孩子,天哪,她简直太棒了!她的乐谱无可挑剔——每个音符都在正确的位置,书写完美,升号、降号都恰到好处,真是太美了。她将来一定会成为一名了不起的音乐家。”
Waking up in a cold sweat, the musician realizes, gratefully, that it was all just a crazy dream. “Of course!” he reassures himself, “No society would ever reduce such a beautiful and meaningful art form to something so mindless and trivial; no culture could be so cruel to its children as to deprive them of such a natural, satisfying means of human expression. How absurd!”
音乐家浑身冷汗地醒来,心怀感激地意识到,这一切都只是一场疯狂的噩梦。“当然!”他安慰自己,“没有哪个社会会把如此美丽而有意义的艺术形式简化成如此空洞乏味、微不足道的东西;没有哪种文化会对自己的孩子如此残忍,剥夺他们这种自然而令人愉悦的人类表达方式。这太荒谬了!”
Meanwhile, on the other side of town, a painter has just awakened from a similar nightmare…
与此同时,在城镇的另一头,一位画家也从一场类似的噩梦中惊醒……
I was surprised to find myself in a regular school classroom- no easels, no tubes of paint. “Oh we don’t actually apply paint until high school,” I was told by the students. “In seventh grade we mostly study colors and applicators.” They showed me a worksheet. On one side were swatches of color with blank spaces next to them. They were told to write in the names. “I like painting,” one of them remarked, “they tell me what to do and I do it. It’s easy!”
我惊讶地发现自己身处一间普通的学校教室——没有画架,没有颜料管。“哦,我们要到高中才真正开始画画呢,”学生们告诉我,“七年级主要是学习颜色和绘画工具。”他们给我看了一张作业纸,一边是各种颜色的色卡,旁边留着空白,要求他们写下颜色的名称。“我喜欢画画,”其中一个学生说,“他们告诉我要做什么,我照做就行,很简单!”
After class I spoke with the teacher. “So your students don’t actually do any painting?” I asked. “Well, next year they take Pre-Paint-by-Numbers. That prepares them for the main Paint-by-Numbers sequence in high school. So they’ll get to use what they’ve learned here and apply it to real-life painting situations- dipping the brush into paint, wiping it off, stuff like that. Of course we track our students by ability. The really excellent painters- the ones who know their colors and brushes backwards and forwards- they get to the actual painting a little sooner, and some of them even take the Advanced Placement classes for college credit. But mostly we’re just trying to give these kids a good foundation in what painting is all about, so when they get out there in the real world and paint their kitchen they don’t make a total mess of it.”
课后我和老师聊了起来。“这么说,你的学生们其实根本不画画?”我问。“嗯,明年他们会学‘数字填色预备课’,为高中的核心数字填色课程做准备。这样他们就能把在这里学到的知识应用到实际的绘画场景中——比如把刷子蘸上颜料,再擦掉多余的,之类的。当然,我们会根据学生的能力进行分层教学。那些真正优秀的画家——也就是对颜色和画笔了如指掌的学生——会更早开始真正的绘画,有些人甚至会参加大学先修课程,以获得大学学分。但总的来说,我们只是想让这些孩子打好绘画基础,这样他们将来在现实生活中给自己的厨房刷漆时,不会弄得一团糟。”
“Um, these high school classes you mentioned…”
“嗯,你说的那些高中课程……”
“You mean Paint-by-Numbers? We’re seeing much higher enrollments lately. I think it’s mostly coming from parents wanting to make sure their kid gets into a good college. Nothing looks better than Advanced Paint-by-Numbers on a high school transcript.”
“你是说数字填色课?最近报名的人多了很多。我觉得主要是因为家长们想确保孩子能进入好大学。高中成绩单上有‘高级数字填色’这门课,看起来可是相当不错的。”
“Why do colleges care if you can fill in numbered regions with the corresponding color?”
“为什么大学会在意你是否能给编号的区域填上对应的颜色呢?”
“Oh, well, you know, it shows clear-headed logical thinking. And of course if a student is planning to major in one of the visual sciences, like fashion or interior decorating, then it’s really a good idea to get your painting requirements out of the way in high school.”
“哦,你知道的,这能体现清晰的逻辑思维能力。当然,如果学生打算主修视觉相关专业,比如时尚设计或室内装饰,那么在高中就完成绘画相关的必修要求,确实是个好主意。”
“I see. And when do students get to paint freely, on a blank canvas?”
“我明白了。那学生们什么时候才能在空白的画布上自由创作呢?”
“You sound like one of my professors! They were always going on about expressing yourself and your feelings and things like that-really way-out-there abstract stuff. I’ve got a degree in Painting myself, but I’ve never really worked much with blank canvasses. I just use the Paint-by-Numbers kits supplied by the school board.”
“你这话听起来像我的大学教授们!他们总是滔滔不绝地谈论自我表达、情感抒发之类的——都是些非常抽象、不着边际的东西。我自己有绘画学位,但从来没怎么在空白画布上创作过。我只用学校董事会提供的数字填色套装。”
Sadly, our present system of mathematics education is precisely this kind of nightmare. In fact, if I had to design a mechanism for the express purpose of destroying a child’s natural curiosity and love of pattern-making, I couldn’t possibly do as good a job as is currently being done- I simply wouldn’t have the imagination to come up with the kind of senseless, soul-crushing ideas that constitute contemporary mathematics education.
可悲的是,我们现行的数学教育体系正是这样一场噩梦。事实上,如果我必须设计一个专门用来摧毁孩子天生的好奇心和对模式探索热爱的机制,我绝对做不到现在这么好——我根本没有想象力能想出那些构成当代数学教育的、毫无意义且摧残心灵的主意。
Everyone knows that something is wrong. The politicians say, “we need higher standards.” The schools say, “we need more money and equipment.” Educators say one thing, and teachers say another. They are all wrong. The only people who understand what is going on are the ones most often blamed and least often heard: the students. They say, “math class is stupid and boring,” and they are right.
每个人都知道哪里出了问题。政客们说:“我们需要更高的标准。”学校说:“我们需要更多的资金和设备。”教育专家们各执一词,老师们也有自己的说法。但他们都错了。唯一明白真相的,是那些最常被指责、却最没人愿意倾听的人:学生们。他们说:“数学课又蠢又无聊”,而他们是对的。
Mathematics and Culture
数学与文化
The first thing to understand is that mathematics is an art. The difference between math and the other arts, such as music and painting, is that our culture does not recognize it as such. Everyone understands that poets, painters, and musicians create works of art, and are expressing themselves in word, image, and sound. In fact, our society is rather generous when it comes to creative expression; architects, chefs, and even television directors are considered to be working artists. So why not mathematicians?
首先要明白的是,数学是一门艺术。数学与音乐、绘画等其他艺术形式的区别在于,我们的文化并不认可它的艺术属性。每个人都知道诗人、画家和音乐家创作艺术作品,通过文字、图像和声音表达自我。事实上,我们的社会对创造性表达相当宽容:建筑师、厨师,甚至电视导演都被视为在职的艺术家。那么,为什么数学家不能呢?
Part of the problem is that nobody has the faintest idea what it is that mathematicians do. The common perception seems to be that mathematicians are somehow connected with science- perhaps they help the scientists with their formulas, or feed big numbers into computers for some reason or other. There is no question that if the world had to be divided into the “poetic dreamers” and the “rational thinkers” most people would place mathematicians in the latter category.
部分问题在于,没有人真正知道数学家到底在做什么。普遍的看法似乎是,数学家多少与科学有关——也许他们帮科学家推导公式,或者出于某种原因把大数字输入电脑。毫无疑问,如果要把世界上的人分为“诗意的梦想家”和“理性的思考者”,大多数人会把数学家归到后一类。
Nevertheless, the fact is that there is nothing as dreamy and poetic, nothing as radical, subversive, and psychedelic, as mathematics. It is every bit as mind blowing as cosmology or physics (mathematicians conceived of black holes long before astronomers actually found any), and allows more freedom of expression than poetry, art, or music (which depend heavily on properties of the physical universe). Mathematics is the purest of the arts, as well as the most misunderstood.
然而,事实是,没有什么比数学更富有梦想与诗意,更激进、颠覆且令人迷醉。它和宇宙学或物理学一样令人震撼(数学家在天文学家真正发现黑洞之前很久就构想过黑洞的存在),而且比诗歌、艺术或音乐提供了更多的表达自由(这些艺术形式严重依赖物理宇宙的属性)。数学是最纯粹的艺术,也是最被误解的艺术。
So let me try to explain what mathematics is, and what mathematicians do. I can hardly do better than to begin with G.H. Hardy’s excellent description:
因此,让我试着解释一下数学是什么,数学家们在做什么。我最好从 G.H. 哈代的精彩描述开始:
A mathematician, like a painter or poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas.
数学家,就像画家或诗人一样,是模式的创造者。如果说他的模式比他们的更持久,那是因为这些模式是用思想构建的。
So mathematicians sit around making patterns of ideas. What sort of patterns? What sort of ideas? Ideas about the rhinoceros? No, those we leave to the biologists. Ideas about language and culture? No, not usually. These things are all far too complicated for most mathematicians’ taste. If there is anything like a unifying aesthetic principle in mathematics, it is this: simple is beautiful. Mathematicians enjoy thinking about the simplest possible things, and the simplest possible things are imaginary.
所以,数学家们四处思索,构建思想的模式。什么样的模式?什么样的思想?关于犀牛的思想?不,那是生物学家的事。关于语言和文化的思想?通常也不是。这些东西对大多数数学家来说都太复杂了。如果说数学中存在某种统一的美学原则,那就是:简单即美。数学家们喜欢思考最简单的事物,而最简单的事物往往是想象出来的。
For example, if I’m in the mood to think about shapes- and I often am- I might imagine a triangle inside a rectangular box:
例如,如果我有心情思考形状——我经常这样——我可能会想象一个矩形盒子里有一个三角形:
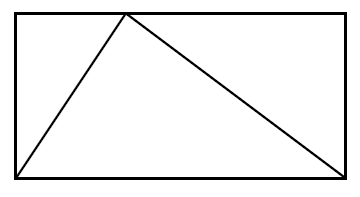
I wonder how much of the box the triangle takes up? Two-thirds maybe? The important thing to understand is that I’m not talking about this drawing of a triangle in a box. Nor am I talking about some metal triangle forming part of a girder system for a bridge. There’s no ulterior practical purpose here. I’m just playing. That’s what math is- wondering, playing, amusing yourself with your imagination. For one thing, the question of how much of the box the triangle takes up doesn’t even make any sense for real, physical objects. Even the most carefully made physical triangle is still a hopelessly complicated collection of jiggling atoms; it changes its size from one minute to the next. That is, unless you want to talk about some sort of approximate measurements. Well, that’s where the aesthetic comes in. That’s just not simple, and consequently it is an ugly question which depends on all sorts of real-world details. Let’s leave that to the scientists. The mathematical question is about an imaginary triangle inside an imaginary box. The edges are perfect because I want them to be- that is the sort of object I prefer to think about. This is a major theme in mathematics: things are what you want them to be. You have endless choices; there is no reality to get in your way.
我想知道这个三角形占据了盒子多大的空间?也许是三分之二?关键要明白的是,我谈论的不是这张画在盒子里的三角形,也不是桥梁梁架系统中某个金属三角形部件。这里没有任何潜在的实际用途,我只是在玩耍。这就是数学——好奇、玩耍、用想象力自娱自乐。首先,对于真实的物理物体来说,“三角形占据盒子多大空间”这个问题本身就没有意义。即使是制作最精良的物理三角形,也只是由不断晃动的原子组成的复杂集合,其大小每时每刻都在变化——除非你想讨论某种近似测量。而这就涉及到美学了:这种问题并不简单,因此是个丑陋的问题,它依赖于各种现实世界的细节。让科学家们去处理这些吧。数学问题关注的是想象中的盒子里那个想象中的三角形。它的边是完美的,因为我希望它们是完美的——这正是我喜欢思考的那种对象。这是数学的一个重要主题:事物可以是你希望的样子。你有无限的选择,没有现实的束缚。
On the other hand, once you have made your choices (for example I might choose to make my triangle symmetrical, or not) then your new creations do what they do, whether you like it or not. This is the amazing thing about making imaginary patterns: they talk back! The triangle takes up a certain amount of its box, and I don’t have any control over what that amount is. There is a number out there, maybe it’s two-thirds, maybe it isn’t, but I don’t get to say what it is. I have to find out what it is.
但另一方面,一旦你做出了选择(比如我可能选择让三角形对称,也可能不选),你新创造的事物就会按其自身规律发展,无论你是否喜欢。这就是构建想象模式的奇妙之处:它们会“回应”你!这个三角形占据了盒子的一定空间,而我无法控制这个空间的大小。存在一个确定的数值,可能是三分之二,也可能不是,但我说了不算,我必须去发现它到底是多少。
So we get to play and imagine whatever we want and make patterns and ask questions about them. But how do we answer these questions? It’s not at all like science. There’s no experiment I can do with test tubes and equipment and whatnot that will tell me the truth about a figment of my imagination. The only way to get at the truth about our imaginations is to use our imaginations, and that is hard work.
因此,我们可以尽情玩耍、畅想,构建各种模式,然后对它们提出问题。但我们如何回答这些问题呢?这和科学完全不同。我无法用试管、设备之类的东西做实验,来验证我想象中的事物的真相。了解我们想象之物真相的唯一方法,就是运用我们的想象力,而这是一项艰巨的工作。
In the case of the triangle in its box, I do see something simple and pretty:
以盒子里的三角形为例,我确实发现了一些简单而优美的规律:
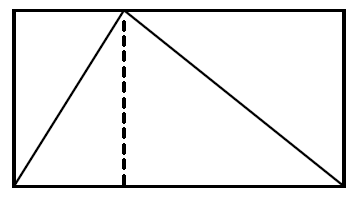
If I chop the rectangle into two pieces like this, I can see that each piece is cut diagonally in half by the sides of the triangle. So there is just as much space inside the triangle as outside. That means that the triangle must take up exactly half the box!
如果我把矩形这样切成两半,就能发现三角形的边把每一半都对角平分了。因此,三角形内部的空间和外部的空间一样大,这意味着三角形恰好占据了盒子的一半空间!
This is what a piece of mathematics looks and feels like. That little narrative is an example of the mathematician’s art: asking simple and elegant questions about our imaginary creations, and crafting satisfying and beautiful explanations. There is really nothing else quite like this realm of pure idea; it’s fascinating, it’s fun, and it’s free!
这就是数学的样子和感觉。这段简短的推理就是数学家艺术的一个例子:对我们想象中的创造物提出简单而优雅的问题,并给出令人满意且优美的解释。这个纯粹的思想领域是独一无二的;它迷人、有趣,而且无拘无束!
Now where did this idea of mine come from? How did I know to draw that line? How does a painter know where to put his brush? Inspiration, experience, trial and error, dumb luck. That’s the art of it, creating these beautiful little poems of thought, these sonnets of pure reason. There is something so wonderfully transformational about this art form. The relationship between the triangle and the rectangle was a mystery, and then that one little line made it obvious. I couldn’t see, and then all of a sudden I could. Somehow, I was able to create a profound simple beauty out of nothing, and change myself in the process. Isn’t that what art is all about?
那么,我的这个想法是从哪里来的?我怎么知道要画那条线?就像画家怎么知道画笔该落在何处一样?答案是灵感、经验、反复尝试,还有一点运气。这就是艺术的本质——创造这些美丽的思想小诗,这些纯粹理性的十四行诗。这种艺术形式具有一种奇妙的变革力量。三角形和矩形之间的关系曾经是个谜,而那条小小的线让一切豁然开朗。我之前一直困惑不解,然后突然间恍然大悟。不知何故,我从无到有地创造出了一种深邃而简单的美,并且在这个过程中改变了自己。这不正是艺术的意义所在吗?
This is why it is so heartbreaking to see what is being done to mathematics in school. This rich and fascinating adventure of the imagination has been reduced to a sterile set of “facts” to be memorized and procedures to be followed. In place of a simple and natural question about shapes, and a creative and rewarding process of invention and discovery, students are treated to this: Triangle Area Formula:
这就是为什么看到学校里对数学所做的一切会如此令人心碎。这场丰富而迷人的想象力冒险,被简化成了一套僵化的“事实”让学生记忆,以及一系列需要遵循的步骤。学生们没有得到关于形状的简单而自然的问题,也没有体验到富有创造性和成就感的发明与发现过程,取而代之的是这个:三角形面积公式:
A
=
1
/
2
b
h
A=1 / 2 \ b \ h
A=1/2 b h
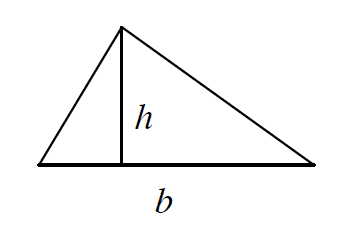
“The area of a triangle is equal to one-half its base times its height.” Students are asked to memorize this formula and then “apply” it over and over in the “exercises.” Gone is the thrill, the joy, even the pain and frustration of the creative act. There is not even a problem anymore. The question has been asked and answered at the same time- there is nothing left for the student to do.
“三角形的面积等于底乘以高的一半。”学生们被要求记住这个公式,然后在“练习题”中反复“应用”。创造性行为带来的兴奋、喜悦,甚至痛苦和挫折感,都消失了。这里甚至不再有“问题”可言——问题和答案同时被给出,学生没有任何可以自主完成的事情。
Now let me be clear about what I’m objecting to. It’s not about formulas, or memorizing interesting facts. That’s fine in context, and has its place just as learning a vocabulary does- it helps you to create richer, more nuanced works of art. But it’s not the fact that triangles take up half their box that matters. What matters is the beautiful idea of chopping it with the line, and how that might inspire other beautiful ideas and lead to creative breakthroughs in other problems- something a mere statement of fact can never give you.
现在我要明确说明我反对的是什么。我反对的不是公式本身,也不是记忆有趣的事实。在合适的语境下,这些都是有益的,就像学习词汇一样——它们能帮助你创造更丰富、更细腻的艺术作品。但重要的不是“三角形占据盒子一半空间”这个事实,而是用线条分割的那个优美想法,以及这个想法如何启发其他优美的思路,并在其他问题中带来创造性的突破——这是单纯陈述事实永远无法给予的。
By removing the creative process and leaving only the results of that process, you virtually guarantee that no one will have any real engagement with the subject. It is like saying that Michelangelo created a beautiful sculpture, without letting me see it. How am I supposed to be inspired by that? (And of course it’s actually much worse than this- at least it’s understood that there is an art of sculpture that I am being prevented from appreciating).
移除创造性过程,只留下过程的结果,你实际上就保证了没有人会真正投入到这门学科中。这就像有人告诉你米开朗基罗创作了一座美丽的雕塑,却不让你亲眼看到它。我怎么可能从中获得灵感呢?(当然,实际情况更糟——至少人们知道雕塑是一门艺术,而我只是被剥夺了欣赏它的机会。)
By concentrating on what, and leaving out why, mathematics is reduced to an empty shell. The art is not in the “truth” but in the explanation, the argument. It is the argument itself which gives the truth its context, and determines what is really being said and meant. Mathematics is the art of explanation. If you deny students the opportunity to engage in this activity- to pose their own problems, make their own conjectures and discoveries, to be wrong, to be creatively frustrated, to have an inspiration, and to cobble together their own explanations and proofs- you deny them mathematics itself. So no, I’m not complaining about the presence of facts and formulas in our mathematics classes, I’m complaining about the lack of mathematics in our mathematics classes.
只关注“是什么”,而忽略“为什么”,数学就变成了一个空洞的外壳。艺术不在于“真相”本身,而在于解释和论证。正是论证赋予了真相语境,决定了它真正的含义。数学是解释的艺术。如果你剥夺了学生参与这种活动的机会——让他们提出自己的问题、做出自己的猜想和发现、犯错、经历创造性的挫折、获得灵感,并拼凑出自己的解释和证明——你就剥夺了他们真正接触数学的机会。因此,我抱怨的不是数学课堂上有事实和公式,而是抱怨我们的数学课堂上缺乏真正的数学。
If your art teacher were to tell you that painting is all about filling in numbered regions, you would know that something was wrong. The culture informs you- there are museums and galleries, as well as the art in your own home. Painting is well understood by society as a medium of human expression. Likewise, if your science teacher tried to convince you that astronomy is about predicting a person’s future based on their date of birth, you would know she was crazy- science has seeped into the culture to such an extent that almost everyone knows about atoms and galaxies and laws of nature. But if your math teacher gives you the impression, either expressly or by default, that mathematics is about formulas and definitions and memorizing algorithms, who will set you straight?
如果你的美术老师告诉你,绘画就是给编号的区域填色,你会立刻知道哪里不对劲。文化会告诉你答案——有博物馆、画廊,还有你家里的艺术品。社会普遍认为绘画是人类表达的一种媒介。同样,如果你的科学老师试图让你相信,天文学是根据一个人的出生日期预测未来,你会知道她疯了——科学已经深深融入文化,几乎每个人都知道原子、星系和自然规律。但如果你的数学老师明确地,或者默认地让你觉得,数学就是公式、定义和记忆算法,谁会来纠正你呢?
The cultural problem is a self-perpetuating monster: students learn about math from their teachers, and teachers learn about it from their teachers, so this lack of understanding and appreciation for mathematics in our culture replicates itself indefinitely. Worse, the perpetuation of this “pseudo-mathematics,” this emphasis on the accurate yet mindless manipulation of symbols, creates its own culture and its own set of values. Those who have become adept at it derive a great deal of self-esteem from their success. The last thing they want to hear is that math is really about raw creativity and aesthetic sensitivity. Many a graduate student has come to grief when they discover, after a decade of being told they were “good at math,” that in fact they have no real mathematical talent and are just very good at following directions. Math is not about following directions, it’s about making new directions.
这个文化问题是一个自我延续的怪物:学生从老师那里学习数学,老师又从他们的老师那里学习数学,因此这种对数学的不理解和不欣赏在我们的文化中无限复制。更糟糕的是,这种“伪数学”的持续存在——强调准确但机械地操纵符号——形成了自己的文化和价值观。那些擅长这种伪数学的人从自己的成功中获得了极大的自尊,他们最不愿意听到的就是“数学本质上是原始的创造力和审美敏感度”。许多研究生在被认为“擅长数学”十年后,突然发现自己其实没有真正的数学天赋,只是非常善于遵循指令,这让他们陷入了痛苦。数学不是遵循指令,而是开辟新的方向。
And I haven’t even mentioned the lack of mathematical criticism in school. At no time are students let in on the secret that mathematics, like any literature, is created by human beings for their own amusement; that works of mathematics are subject to critical appraisal; that one can have and develop mathematical taste. A piece of mathematics is like a poem, and we can ask if it satisfies our aesthetic criteria: Is this argument sound? Does it make sense? Is it simple and elegant? Does it get me closer to the heart of the matter? Of course there’s no criticism going on in school- there’s no art being done to criticize!
我甚至还没提到学校里缺乏数学批评。学生们从来没有被告知这个秘密:数学和任何文学作品一样,是人类为了自娱自乐而创造的;数学作品也需要批判性评价;人们可以拥有并培养数学品味。一篇数学作品就像一首诗,我们可以问:这个论证是否合理?是否有意义?是否简单优雅?是否触及了问题的核心?当然,学校里根本没有这种批评——因为根本没有真正的数学艺术可供批评!
Why don’t we want our children to learn to do mathematics? Is it that we don’t trust them, that we think it’s too hard? We seem to feel that they are capable of making arguments and coming to their own conclusions about Napoleon, why not about triangles? I think it’s simply that we as a culture don’t know what mathematics is. The impression we are given is of something very cold and highly technical, that no one could possibly understand- a self-fulfilling prophesy if there ever was one.
为什么我们不想让孩子们真正去“做”数学?是我们不信任他们,还是觉得数学太难了?我们似乎相信他们有能力就拿破仑的事迹进行论证并得出自己的结论,那为什么不能就三角形进行同样的思考呢?我认为,根本原因在于我们的文化不知道数学到底是什么。我们对数学的印象是冰冷、高度技术化、无人能懂的东西——这是一个彻头彻尾的自我实现的预言。
It would be bad enough if the culture were merely ignorant of mathematics, but what is far worse is that people actually think they do know what math is about- and are apparently under the gross misconception that mathematics is somehow useful to society! This is already a huge difference between mathematics and the other arts. Mathematics is viewed by the culture as some sort of tool for science and technology. Everyone knows that poetry and music are for pure enjoyment and for uplifting and ennobling the human spirit (hence their virtual elimination from the public school curriculum) but no, math is important.
如果文化只是对数学无知,那还不算太糟,但更糟糕的是,人们实际上认为自己知道数学是什么——而且显然存在一个严重的误解,认为数学在某种程度上对社会有用!这已经是数学与其他艺术形式之间的一个巨大差异。文化将数学视为科学和技术的某种工具。每个人都知道诗歌和音乐是为了纯粹的享受,是为了提升和高尚人类的精神(因此它们几乎被排除在公立学校课程之外),但数学不一样,数学很重要。
SIMPLICIO:
Are you really trying to claim that mathematics offers no useful or practical applications to society?
辛普利西奥:
你真的是在说数学对社会没有任何有用或实际的应用吗?
SALVIATI:
Of course not. I’m merely suggesting that just because something happens to have practical consequences, doesn’t mean that’s what it is about. Music can lead armies into battle, but that’s not why people write symphonies. Michelangelo decorated a ceiling, but I’m sure he had loftier things on his mind.
萨尔维亚蒂:
当然不是。我只是想说,仅仅因为某件事恰好有实际效果,并不意味着这就是它的本质目的。音乐可以激励军队奔赴战场,但这并不是人们创作交响乐的原因。米开朗基罗装饰了西斯廷教堂的天顶,但我敢肯定他心中有更崇高的追求。
SIMPLICIO:
But don’t we need people to learn those useful consequences of math? Don’t we need accountants and carpenters and such?
辛普利西奥:
但我们难道不需要人们学习数学那些有用的应用吗?我们难道不需要会计师、木匠之类的人吗?
SALVIATI:
How many people actually use any of this “practical math” they supposedly learn in school? Do you think carpenters are out there using trigonometry? How many adults remember how to divide fractions, or solve a quadratic equation? Obviously the current practical training program isn’t working, and for good reason: it is excruciatingly boring, and nobody ever uses it anyway. So why do people think it’s so important? I don’t see how it’s doing society any good to have its members walking around with vague memories of algebraic formulas and geometric diagrams, and clear memories of hating them. It might do some good, though, to show them something beautiful and give them an opportunity to enjoy being creative, flexible, open-minded thinkers- the kind of thing a real mathematical education might provide.
萨尔维亚蒂:
有多少人真的会用到他们在学校里学到的所谓“实用数学”?你觉得木匠会在工作中使用三角学吗?有多少成年人记得如何分数除法,或者解二次方程?显然,目前的实用培训项目根本不起作用,而且原因很充分:它极其无聊,而且反正没人会用。那么,为什么人们认为它如此重要?让社会成员带着对代数公式和几何图形的模糊记忆,以及对它们的强烈厌恶四处奔走,这对社会有什么好处?然而,如果能向他们展示一些美丽的东西,给他们机会享受成为有创造力、灵活、开放思维的思考者——这正是真正的数学教育所能提供的——那可能会带来一些益处。
SIMPLICIO:
But people need to be able to balance their checkbooks, don’t they?
辛普利西奥:
但人们需要会平衡支票簿,不是吗?
SALVIATI:
I’m sure most people use a calculator for everyday arithmetic. And why not? It’s certainly easier and more reliable. But my point is not just that the current system is so terribly bad, it’s that what it’s missing is so wonderfully good! Mathematics should be taught as art for art’s sake. These mundane “useful” aspects would follow naturally as a trivial by-product. Beethoven could easily write an advertising jingle, but his motivation for learning music was to create something beautiful.
萨尔维亚蒂:
我相信大多数人在日常算术时都会用计算器。为什么不用呢?这当然更简单、更可靠。但我的观点不仅仅是现行制度非常糟糕,更重要的是它缺失了极其美好的东西!数学应该作为一门为艺术而艺术的学科来教授。这些平凡的“有用”方面,自然会作为微不足道的副产品随之而来。贝多芬本可以轻松写出广告歌曲,但他学习音乐的动机是创作美丽的作品。
SIMPLICIO:
But not everyone is cut out to be an artist. What about the kids who aren’t “math people?” How would they fit into your scheme?
辛普利西奥:
但并不是每个人都适合成为艺术家。那些不是“数学型人才”的孩子怎么办?他们在你的方案中如何立足?
SALVIATI:
If everyone were exposed to mathematics in its natural state, with all the challenging fun and surprises that that entails, I think we would see a dramatic change both in the attitude of students toward mathematics, and in our conception of what it means to be “good at math.” We are losing so many potentially gifted mathematicians- creative, intelligent people who rightly reject what appears to be a meaningless and sterile subject. They are simply too smart to waste their time on such piffle.
萨尔维亚蒂:
如果每个人都能接触到数学的本来面目,体验其中蕴含的富有挑战性的乐趣和惊喜,我认为学生对数学的态度,以及我们对“擅长数学”的理解,都会发生巨大的变化。我们正在失去太多有潜力的天才数学家——那些有创造力、聪明的人,他们理所当然地拒绝了这门看似毫无意义、僵化枯燥的学科。他们太聪明了,不会把时间浪费在这种无聊的事情上。
SIMPLICIO:
But don’t you think that if math class were made more like art class that a lot of kids just wouldn’t learn anything?
辛普利西奥:
但你不觉得如果数学课变得更像美术课,很多孩子就什么都学不到了吗?
SALVIATI:
They’re not learning anything now! Better to not have math classes at all than to do what is currently being done. At least some people might have a chance to discover something beautiful on their own.
萨尔维亚蒂:
他们现在本来就什么都没学到!与其现在这样,还不如干脆不上数学课。至少有些人可能有机会自己发现一些美丽的东西。
SIMPLICIO:
So you would remove mathematics from the school curriculum?
辛普利西奥:
所以你想把数学从学校课程中移除?
SALVIATI:
The mathematics has already been removed! The only question is what to do with the vapid, hollow shell that remains. Of course I would prefer to replace it with an active and joyful engagement with mathematical ideas.
萨尔维亚蒂:
数学早就被移除了!唯一的问题是如何处理剩下的这个空洞无物的外壳。当然,我更愿意用一种积极、愉悦的方式去接触数学思想,来取代它。
SIMPLICIO:
But how many math teachers know enough about their subject to teach it that way?
辛普利西奥:
但有多少数学老师对自己的学科足够了解,能够以这种方式教学呢?
SALVIATI: Very few. And that’s just the tip of the iceberg…
萨尔维亚蒂:
非常少。而这仅仅是冰山一角……
Mathematics in School
学校中的数学
There is surely no more reliable way to kill enthusiasm and interest in a subject than to make it a mandatory part of the school curriculum. Include it as a major component of standardized testing and you virtually guarantee that the education establishment will suck the life out of it. School boards do not understand what math is, neither do educators, textbook authors, publishing companies, and sadly, neither do most of our math teachers. The scope of the problem is so enormous, I hardly know where to begin.
要扼杀学生对一门学科的热情和兴趣,最可靠的方法无疑是将其列为学校的必修课。再把它作为标准化考试的主要内容,你实际上就保证了教育机构会彻底榨干它的生命力。学校董事会不理解数学是什么,教育专家、教科书作者、出版公司也不理解,可悲的是,我们大多数数学老师也不理解。这个问题的范围如此之大,我几乎不知道从哪里开始说起。
Let’s start with the “math reform” debacle. For many years there has been a growing awareness that something is rotten in the state of mathematics education. Studies have been commissioned, conferences assembled, and countless committees of teachers, textbook publishers, and educators (whatever they are) have been formed to “fix the problem.” Quite apart from the self-serving interest paid to reform by the textbook industry (which profits from any minute political fluctuation by offering up “new” editions of their unreadable monstrosities), the entire reform movement has always missed the point. The mathematics curriculum doesn’t need to be reformed, it needs to be scrapped.
让我们从“数学改革”的惨败说起。多年来,人们越来越意识到数学教育的现状存在严重问题。研究被委托进行,会议被组织召开,无数由教师、教科书出版商和教育工作者(不管他们到底是什么身份)组成的委员会成立,旨在“解决这个问题”。姑且不论教科书行业对改革的自私利益(他们利用任何微小的政治波动,推出其晦涩难懂的“新”版本来获利),整个改革运动从一开始就偏离了重点。数学课程不需要改革,它需要被彻底废除。
All this fussing and primping about which “topics” should be taught in what order, or the use of this notation instead of that notation, or which make and model of calculator to use, for god’s sake- it’s like rearranging the deck chairs on the Titanic! Mathematics is the music of reason. To do mathematics is to engage in an act of discovery and conjecture, intuition and inspiration; to be in a state of confusion- not because it makes no sense to you, but because you gave it sense and you still don’t understand what your creation is up to; to have a breakthrough idea; to be frustrated as an artist; to be awed and overwhelmed by an almost painful beauty; to be alive, damn it. Remove this from mathematics and you can have all the conferences you like; it won’t matter. Operate all you want, doctors: your patient is already dead.
所有这些关于“主题”应该按什么顺序教授、使用这种符号而不是那种符号、或者使用哪种型号的计算器的小题大做——天哪,这就像在泰坦尼克号上重新排列甲板上的椅子!数学是理性的音乐。做数学就是参与一场发现与猜想、直觉与灵感的行动;是处于一种困惑状态——不是因为它对你毫无意义,而是因为你赋予了它意义,却仍然不理解你自己的创造物在做什么;是获得突破性的想法;是像艺术家一样感到挫折;是被一种近乎令人痛苦的美所震撼和折服;是真正地活着!把这些从数学中移除,你可以召开无数次会议,但都无济于事。医生们,随便你们怎么手术:你们的病人已经死了。
The saddest part of all this “reform” are the attempts to “make math interesting” and “relevant to kids’ lives.” You don’t need to make math interesting- it’s already more interesting than we can handle! And the glory of it is its complete irrelevance to our lives. That’s why it’s so fun!
所有这些“改革”中最可悲的部分,是那些试图“让数学变得有趣”和“与孩子们的生活相关”的努力。你不需要让数学变得有趣——它本身就比我们所能承受的更有趣!而它的魅力正在于其与我们生活的完全无关性。这就是它如此有趣的原因!
Attempts to present mathematics as relevant to daily life inevitably appear forced and contrived: “You see kids, if you know algebra then you can figure out how old Maria is if we know that she is two years older than twice her age seven years ago!” (As if anyone would ever have access to that ridiculous kind of information, and not her age.) Algebra is not about daily life, it’s about numbers and symmetry- and this is a valid pursuit in and of itself:
试图将数学呈现为与日常生活相关的努力,不可避免地显得牵强附会:“孩子们,你们看,如果你懂代数,那么如果我们知道玛丽亚比她七年前年龄的两倍大两岁,你就能算出她现在多大了!”(仿佛有人会知道这种荒谬的信息,却不知道她的实际年龄。)代数与日常生活无关,它是关于数字和对称性的——而这本身就是一项有价值的追求:
Suppose I am given the sum and difference of two numbers. How can I figure out what the numbers are themselves?
假设我知道两个数的和与差,我如何才能算出这两个数本身?
Here is a simple and elegant question, and it requires no effort to be made appealing. The ancient Babylonians enjoyed working on such problems, and so do our students. (And I hope you will enjoy thinking about it too!) We don’t need to bend over backwards to give mathematics relevance. It has relevance in the same way that any art does: that of being a meaningful human experience.
这是一个简单而优雅的问题,无需费力就能吸引人。古代巴比伦人喜欢研究这类问题,我们的学生也一样。(我希望你也会喜欢思考它!)我们不需要费尽心机地让数学变得“相关”。它的相关性就像任何艺术形式一样:是一种有意义的人类体验。
In any case, do you really think kids even want something that is relevant to their daily lives? You think something practical like compound interest is going to get them excited? People enjoy fantasy, and that is just what mathematics can provide- a relief from daily life, an anodyne to the practical workaday world.
无论如何,你真的认为孩子们想要与日常生活相关的东西吗?你觉得复利这样实用的东西会让他们兴奋吗?人们喜欢幻想,而这正是数学所能提供的——一种从日常生活中解脱出来的方式,一种对务实的工作日世界的慰藉。
A similar problem occurs when teachers or textbooks succumb to “cutesyness.” This is where, in an attempt to combat so-called “math anxiety” (one of the panoply of diseases which are actually caused by school), math is made to seem “friendly.” To help your students memorize formulas for the area and circumference of a circle, for example, you might invent this whole story about “Mr. C,” who drives around “Mrs. A” and tells her how nice his “two pies are” (
C
=
2
π
r
C=2 \pi r
C=2πr ) and how her “pies are square” (
A
=
π
r
2
A=\pi r^{2}
A=πr2 ) or some such nonsense. But what about the real story? The one about mankind’s struggle with the problem of measuring curves; about Eudoxus and Archimedes and the method of exhaustion; about the transcendence of pi? Which is more interesting- measuring the rough dimensions of a circular piece of graph paper, using a formula that someone handed you without explanation (and made you memorize and practice over and over) or hearing the story of one of the most beautiful, fascinating problems, and one of the most brilliant and powerful ideas in human history? We’re killing people’s interest in circles for god’s sake!
当教师或教科书陷入“卖萌”的误区时,会出现类似的问题。为了应对所谓的“数学焦虑”(这是一系列实际上由学校造成的“疾病”之一),数学被塑造成“友好”的样子。例如,为了帮助学生记住圆的面积和周长公式,你可能会编造一个关于“C 先生”的完整故事,他开车载着“A 夫人”,告诉她他的“两个派真好吃”(
C
=
2
π
r
C=2 \pi r
C=2πr ),以及她的“派是方形的”(
A
=
π
r
2
A=\pi r^{2}
A=πr2 )之类的无稽之谈。但真正的故事是什么呢?是人类与曲线测量问题的斗争;是欧多克索斯、阿基米德和穷竭法;是圆周率的超越性?哪一个更有趣——用一个别人毫无解释就塞给你(还让你反复记忆和练习)的公式,去测量一张圆形坐标纸的大致尺寸,还是聆听人类历史上最美丽、最迷人的问题之一,以及最卓越、最强大的思想之一的故事?天哪,我们正在扼杀人们对圆的兴趣!
Why aren’t we giving our students a chance to even hear about these things, let alone giving them an opportunity to actually do some mathematics, and to come up with their own ideas, opinions, and reactions? What other subject is routinely taught without any mention of its history, philosophy, thematic development, aesthetic criteria, and current status? What other subject shuns its primary sources- beautiful works of art by some of the most creative minds in history- in favor of third-rate textbook bastardizations?
为什么我们不给学生一个机会去了解这些事情,更不用说让他们有机会真正做一些数学,提出自己的想法、观点和反应呢?还有哪门学科在教学时,通常不提及它的历史、哲学、主题发展、审美标准和现状?还有哪门学科会回避其原始资料——那些由历史上最具创造力的头脑所创造的美丽艺术作品——而偏爱三流的教科书篡改版本?
The main problem with school mathematics is that there are no problems. Oh, I know what passes for problems in math classes, these insipid “exercises.” “Here is a type of problem. Here is how to solve it. Yes it will be on the test. Do exercises 1-35 odd for homework.” What a sad way to learn mathematics: to be a trained chimpanzee.
学校数学的主要问题是“没有问题”。哦,我知道数学课上所谓的“问题”是什么——那些枯燥乏味的“练习题”。“这是一种题型,这是解题方法。这个知识点会考试。作业做 1 到 35 题的奇数题。”这是一种多么可悲的学习数学的方式:像一只训练有素的黑猩猩。
But a problem, a genuine honest-to-goodness natural human question- that’s another thing. How long is the diagonal of a cube? Do prime numbers keep going on forever? Is infinity a number? How many ways can I symmetrically tile a surface? The history of mathematics is the history of mankind’s engagement with questions like these, not the mindless regurgitation of formulas and algorithms (together with contrived exercises designed to make use of them).
但一个真正的、发自内心的、自然的人类问题——那是另一回事。立方体的对角线有多长?质数会无限延续下去吗?无穷大是一个数吗?我有多少种方法可以对称地铺砌一个平面?数学的历史就是人类探索这类问题的历史,而不是对公式和算法的机械复述(以及为了应用它们而设计的刻意练习题)。
A good problem is something you don’t know how to solve. That’s what makes it a good puzzle, and a good opportunity. A good problem does not just sit there in isolation, but serves as a springboard to other interesting questions. A triangle takes up half its box. What about a pyramid inside its three-dimensional box? Can we handle this problem in a similar way?
一个好的问题是你不知道如何解决的问题。这正是它成为一个好谜题、一个好机会的原因。一个好的问题不会孤立存在,而是会成为通往其他有趣问题的跳板。三角形占据了盒子的一半空间,那么三维盒子里的金字塔呢?我们能用类似的方法解决这个问题吗?
I can understand the idea of training students to master certain techniques- I do that too. But not as an end in itself. Technique in mathematics, as in any art, should be learned in context. The great problems, their history, the creative process- that is the proper setting. Give your students a good problem, let them struggle and get frustrated. See what they come up with. Wait until they are dying for an idea, then give them some technique. But not too much.
我理解训练学生掌握特定技巧的想法——我也会这么做。但这不能作为最终目的。数学中的技巧,就像任何艺术形式中的技巧一样,应该在具体情境中学习。伟大的问题、它们的历史、创造性的过程——这才是合适的背景。给你的学生一个好问题,让他们去挣扎、去受挫。看看他们能想出什么。等到他们迫切需要一个思路时,再给他们一些技巧。但不要给太多。
So put away your lesson plans and your overhead projectors, your full-color textbook abominations, your CD-ROMs and the whole rest of the traveling circus freak show of contemporary education, and simply do mathematics with your students! Art teachers don’t waste their time with textbooks and rote training in specific techniques. They do what is natural to their subject- they get the kids painting. They go around from easel to easel, making suggestions and offering guidance:
所以,扔掉你的教案和投影仪,扔掉你那些彩色的、令人作呕的教科书,扔掉你的光盘和当代教育中所有其他华而不实的噱头, simply 和你的学生一起做数学吧!美术老师不会把时间浪费在教科书和特定技巧的死记硬背上。他们做的是与自己学科本质相符的事情——让孩子们画画。他们在画架之间来回走动,提出建议,提供指导:
“I was thinking about our triangle problem, and I noticed something. If the triangle is really slanted then it doesn’t take up half it’s box! See, look:
“我一直在想我们的三角形问题,然后发现了一个现象。如果这个三角形非常倾斜,它就不会占据盒子的一半空间了!你看:
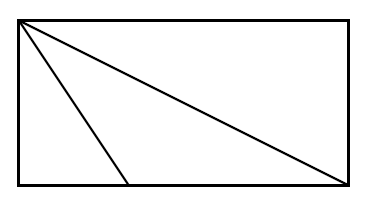
“Excellent observation! Our chopping argument assumes that the tip of the triangle lies directly over the base. Now we need a new idea.”
“非常棒的发现!我们之前的分割论证假设三角形的顶点正好在底边的正上方。现在我们需要一个新的思路。”
“Should I try chopping it a different way?”
“我应该尝试用不同的方式分割吗?”
“Absolutely. Try all sorts of ideas. Let me know what you come up with!”
“当然。尝试各种想法,有结果了告诉我!”
To make discoveries and formulate conjectures. By helping them to refine their arguments and creating an atmosphere of healthy and vibrant mathematical criticism. By being flexible and open to sudden changes in direction to which their curiosity may lead. In short, by having an honest intellectual relationship with our students and our subject. So how do we teach our students to do mathematics? By choosing engaging and natural problems suitable to their tastes, personalities, and level of experience. By giving them time
要让学生去发现、去提出猜想。通过帮助他们完善自己的论证,创造一种健康、活跃的数学批评氛围。通过保持灵活性,对他们的好奇心可能引领的突然方向转变持开放态度。简而言之,通过与我们的学生和我们的学科建立一种真诚的智力交流关系。那么,我们如何教学生做数学呢?通过选择适合他们兴趣、个性和经验水平的、有吸引力且自然的问题。通过给他们足够的时间。
Of course what I’m suggesting is impossible for a number of reasons. Even putting aside the fact that statewide curricula and standardized tests virtually eliminate teacher autonomy, I doubt that most teachers even want to have such an intense relationship with their students. It requires too much vulnerability and too much responsibility- in short, it’s too much work!
当然,我所建议的事情由于多种原因是不可能实现的。暂且不说全州统一的课程和标准化考试实际上剥夺了教师的自主权,我怀疑大多数教师甚至并不想与学生建立如此紧密的关系。这需要太多的投入和责任——简而言之,工作量太大了!
It is far easier to be a passive conduit of some publisher’s “materials” and to follow the shampoo-bottle instruction “lecture, test, repeat” than to think deeply and thoughtfully about the meaning of one’s subject and how best to convey that meaning directly and honestly to one’s students. We are encouraged to forego the difficult task of making decisions based on our individual wisdom and conscience, and to “get with the program.” It is simply the path of least resistance:
做一个出版商“教材”的被动传递者,遵循“讲课、考试、重复”这种洗发水式的指令,要比深入思考自己学科的意义,以及如何最好地将这种意义直接、诚实地传达给学生容易得多。我们被鼓励放弃基于个人智慧和良知做决定的艰难任务,而是“按流程办事”。这只是最省力的路径:
TEXTBOOK PUBLISHERS : TEACHERS ::
教科书出版商 : 教师 ::
A) pharmaceutical companies : doctors
A) 制药公司 : 医生
B) record companies : disk jockeys
B) 唱片公司 : 电台 DJ
C) corporations : congressmen
C) 企业 : 国会议员
D) all of the above
D) 以上皆是
The trouble is that math, like painting or poetry, is hard creative work. That makes it very difficult to teach. Mathematics is a slow, contemplative process. It takes time to produce a work of art, and it takes a skilled teacher to recognize one. Of course it’s easier to post a set of rules than to guide aspiring young artists, and it’s easier to write a VCR manual than to write an actual book with a point of view.
问题在于,数学就像绘画或诗歌一样,是艰苦的创造性工作。这使得它很难被教授。数学是一个缓慢、沉思的过程。创作一件艺术作品需要时间,而识别一件艺术作品则需要一位有技巧的教师。当然,发布一套规则比指导有抱负的年轻艺术家更容易,写一本录像机说明书也比写一本有观点的真正书籍更容易。
Mathematics is an art, and art should be taught by working artists, or if not, at least by people who appreciate the art form and can recognize it when they see it. It is not necessary that you learn music from a professional composer, but would you want yourself or your child to be taught by someone who doesn’t even play an instrument, and has never listened to a piece of music in their lives? Would you accept as an art teacher someone who has never picked up a pencil or stepped foot in a museum? Why is it that we accept math teachers who have never produced an original piece of mathematics, know nothing of the history and philosophy of the subject, nothing about recent developments, nothing in fact beyond what they are expected to present to their unfortunate students? What kind of a teacher is that? How can someone teach something that they themselves don’t do? I can’t dance, and consequently I would never presume to think that I could teach a dance class (I could try, but it wouldn’t be pretty). The difference is I know I can’t dance. I don’t have anyone telling me I’m good at dancing just because I know a bunch of dance words.
数学是一门艺术,而艺术应该由在职的艺术家来教授;如果做不到这一点,至少也应该由那些欣赏这种艺术形式、并且能识别它的人来教授。你不一定需要从专业作曲家那里学习音乐,但你会希望自己或你的孩子被一个甚至不会演奏乐器、一生中从未听过一首音乐的人教授音乐吗?你会接受一个从未拿起过画笔、从未踏入过博物馆的人作为美术老师吗?为什么我们会接受那些从未创造过任何原创数学作品、对数学的历史和哲学一无所知、对最新发展毫无了解、实际上除了要教给不幸学生的那些内容之外一无所知的数学老师?这是什么样的老师?一个人怎么能教授自己都不会做的事情?我不会跳舞,因此我绝不会冒昧地认为自己能教舞蹈课(我可以试试,但结果肯定很糟糕)。不同之处在于,我知道自己不会跳舞。不会有人因为我知道一堆舞蹈术语,就告诉我我擅长跳舞。
Now I’m not saying that math teachers need to be professional mathematicians- far from it. But shouldn’t they at least understand what mathematics is, be good at it, and enjoy doing it?
我并不是说数学老师需要是专业的数学家——远非如此。但他们至少应该理解数学是什么,擅长数学,并且喜欢做数学,难道不是吗?
If teaching is reduced to mere data transmission, if there is no sharing of excitement and wonder, if teachers themselves are passive recipients of information and not creators of new ideas, what hope is there for their students? If adding fractions is to the teacher an arbitrary set of rules, and not the outcome of a creative process and the result of aesthetic choices and desires, then of course it will feel that way to the poor students.
如果教学被简化为单纯的数据传输,如果没有对兴奋和惊奇的分享,如果教师自己只是信息的被动接收者,而不是新思想的创造者,那么他们的学生还有什么希望?如果分数加法对教师来说只是一套任意的规则,而不是创造性过程的结果,不是审美选择和渴望的产物,那么对于可怜的学生来说,它当然也会是这个样子。
Teaching is not about information. It’s about having an honest intellectual relationship with your students. It requires no method, no tools, and no training. Just the ability to be real. And if you can’t be real, then you have no right to inflict yourself upon innocent children.
教学无关乎信息传递。它关乎与你的学生建立一种真诚的智力交流关系。它不需要方法、工具或培训。只需要真诚待人的能力。如果你不能真诚待人,那么你就没有权利把自己强加给无辜的孩子。
In particular, you can’t teach teaching. Schools of education are a complete crock. Oh, you can take classes in early childhood development and whatnot, and you can be trained to use a blackboard “effectively” and to prepare an organized “lesson plan” (which, by the way, insures that your lesson will be planned, and therefore false), but you will never be a real teacher if you are unwilling to be a real person. Teaching means openness and honesty, an ability to share excitement, and a love of learning. Without these, all the education degrees in the world won’t help you, and with them they are completely unnecessary.
特别是,你无法“教授”教学本身。教育学院完全是一派胡言。哦,你可以上幼儿发展之类的课程,你可以接受培训,学习“有效”使用黑板,准备有条理的“教案”(顺便说一句,这确保了你的课是被计划好的,因此是不真实的),但如果你不愿意做一个真诚的人,你永远也成不了一名真正的教师。教学意味着开放和诚实,意味着分享兴奋的能力,意味着对学习的热爱。没有这些,世界上所有的教育学位都帮不了你;而有了这些,学位就完全没有必要了。
It’s perfectly simple. Students are not aliens. They respond to beauty and pattern, and are naturally curious like anyone else. Just talk to them! And more importantly, listen to them!
这非常简单。学生不是外星人。他们对美和模式有反应,和其他人一样天生好奇。只要和他们交流!更重要的是,倾听他们的声音!
SIMPLICIO:
All right, I understand that there is an art to mathematics and that we are not doing a good job of exposing people to it. But isn’t this a rather esoteric, highbrow sort of thing to expect from our school system? We’re not trying to create philosophers here, we just want people to have a reasonable command of basic arithmetic so they can function in society.
辛普利西奥:
好吧,我明白数学是一门艺术,而我们在让人们接触这门艺术方面做得并不好。但期望我们的学校系统提供这种深奥、高雅的东西,难道不是有点不切实际吗?我们不是要培养哲学家,我们只是想让人们掌握基本的算术,以便他们能在社会中正常生活。
SALVIATI:
But that’s not true! School mathematics concerns itself with many things that have nothing to do with the ability to get along in society- algebra and trigonometry, for instance. These studies are utterly irrelevant to daily life. I’m simply suggesting that if we are going to include such things as part of most students’ basic education, that we do it in an organic and natural way. Also, as I said before, just because a subject happens to have some mundane practical use does not mean that we have to make that use the focus of our teaching and learning. It may be true that you have to be able to read in order to fill out forms at the DMV, but that’s not why we teach children to read. We teach them to read for the higher purpose of allowing them access to beautiful and meaningful ideas. Not only would it be cruel to teach reading in such a way- to force third graders to fill out purchase orders and tax forms- it wouldn’t work! We learn things because they interest us now, not because they might be useful later. But this is exactly what we are asking children to do with math.
萨尔维亚蒂:
但这不是事实!学校数学涉及许多与社会生存能力无关的内容——比如代数和三角学。这些学习内容与日常生活完全无关。我只是建议,如果我们要将这些内容纳入大多数学生的基础教育,就应该以一种有机、自然的方式进行。此外,正如我之前所说,仅仅因为一门学科恰好有一些平凡的实际用途,并不意味着我们必须将这种用途作为教学的重点。诚然,你需要会阅读才能在车管所填写表格,但这并不是我们教孩子阅读的原因。我们教他们阅读,是为了更高层次的目的——让他们能够接触到美丽而有意义的思想。如果以那种方式教阅读——强迫三年级学生填写采购订单和纳税申报表——不仅残忍,而且行不通!我们学习东西是因为它们现在能引起我们的兴趣,而不是因为它们以后可能有用。但这正是我们要求孩子们在数学学习中做的事情。
SIMPLICIO:
But don’t we need third graders to be able to do arithmetic?
辛普利西奥:
但我们难道不需要三年级学生学会算术吗?
SALVIATI:
Why? You want to train them to calculate 427 plus 389? It’s just not a question that very many eight-year-olds are asking. For that matter, most adults don’t fully understand decimal place-value arithmetic, and you expect third graders to have a clear conception? Or do you not care if they understand it? It is simply too early for that kind of technical training. Of course it can be done, but I think it ultimately does more harm than good. Much better to wait until their own natural curiosity about numbers kicks in.
萨尔维亚蒂:
为什么?你想训练他们计算 427 加 389?这并不是很多八岁孩子会问的问题。事实上,大多数成年人都没有完全理解十进制位值算术,你却期望三年级学生有清晰的概念?或者你根本不在乎他们是否理解?进行这种技术训练还为时过早。当然,这是可以做到的,但我认为最终弊大于利。最好等到他们自己对数字产生自然的好奇心时再进行。
SIMPLICIO:
Then what should we do with young children in math class?
辛普利西奥:
那么,我们应该让小孩子在数学课上做什么呢?
SALVIATI:
Play games! Teach them Chess and Go, Hex and Backgammon, Sprouts and Nim, whatever. Make up a game. Do puzzles. Expose them to situations where deductive reasoning is necessary. Don’t worry about notation and technique, help them to become active and creative mathematical thinkers.
萨尔维亚蒂:
玩游戏!教他们国际象棋、围棋、六贯棋、双陆棋、芽苗棋、尼姆游戏,什么都行。自己编游戏,做谜题。让他们接触需要演绎推理的情境。不要担心符号和技巧,帮助他们成为积极、有创造力的数学思考者。
SIMPLICIO:
It seems like we’d be taking an awful risk. What if we de-emphasize arithmetic so much that our students end up not being able to add and subtract?
辛普利西奥:
这似乎是在冒很大的风险。如果我们如此淡化算术,以至于我们的学生最终不会加减运算,怎么办?
SALVIATI:
I think the far greater risk is that of creating schools devoid of creative expression of any kind, where the function of the students is to memorize dates, formulas, and vocabulary lists, and then regurgitate them on standardized tests-“Preparing tomorrow’s workforce today!”
萨尔维亚蒂:
我认为更大的风险是创建一所缺乏任何形式创造性表达的学校,在那里,学生的职责就是记忆日期、公式和词汇表,然后在标准化考试中复述出来——“今天为明天的劳动力做准备!”
SIMPLICIO:
But surely there is some body of mathematical facts of which an educated person should be cognizant.
辛普利西奥:
但一个受过教育的人肯定应该了解一些数学事实,不是吗?
SALVIATI:
Yes, the most important of which is that mathematics is an art form done by human beings for pleasure! Alright, yes, it would be nice if people knew a few basic things about numbers and shapes, for instance. But this will never come from rote memorization, drills, lectures, and exercises. You learn things by doing them and you remember what matters to you. We have millions of adults wandering around with “negative b plus or minus the square root of b squared minus
4
a
c
4 a c
4ac all over
2
a
2 a
2a ” in their heads, and absolutely no idea whatsoever what it means. And the reason is that they were never given the chance to discover or invent such things for themselves. They never had an engaging problem to think about, to be frustrated by, and to create in them the desire for technique or method. They were never told the history of mankind’s relationship with numbers- no ancient Babylonian problem tablets, no Rhind Papyrus, no Liber Abaci, no Ars Magna. More importantly, no chance for them to even get curious about a question; it was answered before they could ask it.
萨尔维亚蒂:
是的,其中最重要的一点是,数学是人类为了乐趣而创造的一种艺术形式!好吧,当然,如果人们能了解一些关于数字和形状的基本知识,那会很好。但这永远不会来自死记硬背、反复训练、讲座和练习。你通过实践学习东西,并且记住对你重要的东西。我们有数百万成年人,脑子里记得“负 b 加减 b 平方减
4
a
c
4 a c
4ac 的平方根,再除以
2
a
2 a
2a ”,却完全不知道这是什么意思。原因是他们从未有机会自己发现或发明这些东西。他们从未有过一个有吸引力的问题去思考、去为之受挫,并在心中产生对技巧或方法的渴望。他们从未被告知人类与数字关系的历史——没有古代巴比伦的问题泥板,没有林德纸草书,没有《计算之书》,没有《大术》。更重要的是,他们甚至没有机会对一个问题产生好奇;问题在他们提出之前就已经有了答案。
SIMPLICIO:
But we don’t have time for every student to invent mathematics for themselves! It took centuries for people to discover the Pythagorean Theorem. How can you expect the average child to do it?
辛普利西奥:
但我们没有时间让每个学生都自己发明数学!人类花了几个世纪才发现勾股定理。你怎么能期望普通孩子做到这一点呢?
SALVIATI:
I don’t. Let’s be clear about this. I’m complaining about the complete absence of art and invention, history and philosophy, context and perspective from the mathematics curriculum. That doesn’t mean that notation, technique, and the development of a knowledge base have no place. Of course they do. We should have both. If I object to a pendulum being too far to one side, it doesn’t mean I want it to be all the way on the other side. But the fact is, people learn better when the product comes out of the process. A real appreciation for poetry does not come from memorizing a bunch of poems, it comes from writing your own.
萨尔维亚蒂:
我没有这样期望。让我们把话说清楚。我抱怨的是数学课程中完全缺乏艺术与发明、历史与哲学、背景与视角。这并不意味着符号、技巧和知识体系的构建没有立足之地。当然有。我们两者都需要。如果我反对钟摆摆得太偏一边,并不意味着我希望它摆到另一边。但事实是,当成果来自过程本身时,人们学得更好。对诗歌的真正欣赏不是来自背诵一堆诗歌,而是来自自己写诗。
SIMPLICIO:
Yes, but before you can write your own poems you need to learn the alphabet. The process has to begin somewhere. You have to walk before you can run.
辛普利西奥:
是的,但在你能自己写诗之前,你需要先学习字母表。学习过程总得有个起点。你得先会走,才能跑。
SALVIATI:
No, you have to have something you want to run toward. Children can write poems and stories as they learn to read and write. A piece of writing by a six-year-old is a wonderful thing, and the spelling and punctuation errors don’t make it less so. Even very young children can invent songs, and they haven’t a clue what key it is in or what type of meter they are using.
萨尔维亚蒂:
不,你得有一个想要奔向的目标。孩子们在学习读写的过程中,就可以写诗歌和故事了。一个六岁孩子的作品是很美妙的,拼写和标点错误并不会减损它的价值。即使是非常年幼的孩子,也能创作歌曲,尽管他们完全不知道自己用的是什么调式,或者是什么节拍类型。
SIMPLICIO:
But isn’t math different? Isn’t math a language of its own, with all sorts of symbols that have to be learned before you can use it?
辛普利西奥:
但数学不一样,不是吗?数学本身就是一种语言,有各种各样的符号,你必须先学会这些符号才能使用它,不是吗?
SALVIATI:
Not at all. Mathematics is not a language, it’s an adventure. Do musicians “speak another language” simply because they choose to abbreviate their ideas with little black dots? If so, it’s no obstacle to the toddler and her song. Yes, a certain amount of mathematical shorthand has evolved over the centuries, but it is in no way essential. Most mathematics is done with a friend over a cup of coffee, with a diagram scribbled on a napkin. Mathematics is and always has been about ideas, and a valuable idea transcends the symbols with which you choose to represent it. As Gauss once remarked, “What we need are notions, not notations.”
萨尔维亚蒂:
完全不是。数学不是一种语言,而是一场冒险。难道音乐家仅仅因为用小黑点来简化记录自己的想法,就等于“说另一种语言”吗?如果是这样,这对蹒跚学步的孩子唱歌也没有阻碍。诚然,几个世纪以来,数学确实发展出了一些简化符号,但这些符号绝非必不可少。大多数数学思考,都是和朋友喝着咖啡,在餐巾纸上随手画个图完成的。数学过去是、现在也是关于思想的学科,一个有价值的思想,不会受限于你选择用来表达它的符号。正如高斯曾经说过的:“我们需要的是思想,不是符号。”
SIMPLICIO:
But isn’t one of the purposes of mathematics education to help students think in a more precise and logical way, and to develop their “quantitative reasoning skills?” Don’t all of these definitions and formulas sharpen the minds of our students?
辛普利西奥:
但数学教育的目的之一,不就是帮助学生更精确、更有逻辑地思考,培养他们的“定量推理能力”吗?难道这些定义和公式不能让学生的思维更敏锐吗?
SALVIATI:
No they don’t. If anything, the current system has the opposite effect of dulling the mind. Mental acuity of any kind comes from solving problems yourself, not from being told how to solve them.
萨尔维亚蒂:
不能。事实上,现行的教育体系反而会产生让思维变得迟钝的相反效果。任何形式的思维敏锐度,都来自于自己解决问题,而不是别人告诉你如何解决问题。
SIMPLICIO:
Fair enough. But what about those students who are interested in pursuing a career in science or engineering? Don’t they need the training that the traditional curriculum provides? Isn’t that why we teach mathematics in school?
辛普利西奥:
有道理。但那些想从事科学或工程领域职业的学生呢?他们不需要传统课程提供的训练吗?我们在学校教数学,不就是为了这个吗?
SALVIATI:
How many students taking literature classes will one day be writers? That is not why we teach literature, nor why students take it. We teach to enlighten everyone, not to train only the future professionals. In any case, the most valuable skill for a scientist or engineer is being able to think creatively and independently. The last thing anyone needs is to be trained.
萨尔维亚蒂:
有多少上文学课的学生,将来会成为作家?这既不是我们教文学的原因,也不是学生学文学的原因。我们教书是为了启发所有人,而不仅仅是培养未来的专业人士。无论如何,对科学家或工程师来说,最有价值的技能是能够创造性地独立思考。没有人需要的是“被训练”。
The Mathematics Curriculum
数学课程体系
The truly painful thing about the way mathematics is taught in school is not what is missing- the fact that there is no actual mathematics being done in our mathematics classes- but what is there in its place: the confused heap of destructive disinformation known as “the mathematics curriculum.” It is time now to take a closer look at exactly what our students are up against- what they are being exposed to in the name of mathematics, and how they are being harmed in the process.
学校教授数学的方式中,真正令人痛苦的不是缺失的部分——我们的数学课上根本没有真正的数学实践——而是取而代之的东西:那堆混乱不堪、具有破坏性的错误信息,也就是所谓的“数学课程体系”。现在,是时候仔细看看我们的学生到底面临着什么了——看看他们在“数学”的名义下接触到的是什么,以及这个过程中他们受到了怎样的伤害。
The most striking thing about this so-called mathematics curriculum is its rigidity. This is especially true in the later grades. From school to school, city to city, and state to state, the same exact things are being said and done in the same exact way and in the same exact order. Far from being disturbed and upset by this Orwellian state of affairs, most people have simply accepted this “standard model” math curriculum as being synonymous with math itself.
这个所谓的数学课程体系,最显著的特点就是它的僵化。在高年级尤其如此。无论在哪个学校、哪个城市、哪个州,教授的内容、方式和顺序都完全一样。大多数人非但没有对这种奥威尔式的现状感到不安或不满,反而简单地将这种“标准模式”的数学课程等同于数学本身。
This is intimately connected to what I call the “ladder myth”- the idea that mathematics can be arranged as a sequence of “subjects” each being in some way more advanced, or “higher” than the previous. The effect is to make school mathematics into a race- some students are “ahead” of others, and parents worry that their child is “falling behind.” And where exactly does this race lead? What is waiting at the finish line? It’s a sad race to nowhere. In the end you’ve been cheated out of a mathematical education, and you don’t even know it.
这与我所说的“阶梯神话”密切相关——这种观点认为,数学可以被安排成一系列“学科”,每个学科在某种程度上都比前一个更“高级”。其结果是,学校数学变成了一场竞赛——有些学生比其他学生“领先”,家长则担心自己的孩子“落后”。但这场竞赛到底通向哪里?终点线后有什么在等待?这是一场可悲的、没有目的地的竞赛。最终,你被剥夺了真正的数学教育,却一无所知。
Real mathematics doesn’t come in a can- there is no such thing as an Algebra II idea. Problems lead you to where they take you. Art is not a race. The ladder myth is a false image of the subject, and a teacher’s own path through the standard curriculum reinforces this myth and prevents him or her from seeing mathematics as an organic whole. As a result, we have a math curriculum with no historical perspective or thematic coherence, a fragmented collection of assorted topics and techniques, united only by the ease in which they can be reduced to step-by-step procedures.
真正的数学不是预制好的罐头——不存在“代数 II 专属思想”这种东西。问题会引导你走向它该去的地方。艺术不是竞赛。“阶梯神话”是对数学这门学科的错误描绘,而教师自己沿着标准课程体系走过的路径,又强化了这种神话,使他们无法将数学视为一个有机的整体。结果就是,我们的数学课程体系没有历史视角,也没有主题连贯性,只是一堆零散的主题和技巧的集合,唯一的共同点是它们都能轻易地被简化成一步步的流程。
In place of discovery and exploration, we have rules and regulations. We never hear a student saying, “I wanted to see if it could make any sense to raise a number to a negative power, and I found that you get a really neat pattern if you choose it to mean the reciprocal.” Instead we have teachers and textbooks presenting the “negative exponent rule” as a fait d’accompli with no mention of the aesthetics behind this choice, or even that it is a choice.
我们用规则和条例取代了发现与探索。你永远不会听到学生说:“我想知道给一个数取负指数是否有意义,然后发现如果把它定义为倒数,会得到一个非常简洁的规律。”相反,教师和教科书会把“负指数法则”当作既成事实来呈现,完全不提这个选择背后的美学考量,甚至不提这是一种“选择”。
In place of meaningful problems, which might lead to a synthesis of diverse ideas, to uncharted territories of discussion and debate, and to a feeling of thematic unity and harmony in mathematics, we have instead joyless and redundant exercises, specific to the technique under discussion, and so disconnected from each other and from mathematics as a whole that neither the students nor their teacher have the foggiest idea how or why such a thing might have come up in the first place.
我们用枯燥冗余的练习题,取代了有意义的问题——那些本可以融合不同思想、通向未知的讨论与辩论领域、让人感受到数学主题统一性与和谐性的问题。这些练习题只针对当前教授的技巧,彼此之间、与数学整体之间都毫无关联,以至于学生和教师都完全不知道,这些内容最初是如何、为何会出现的。
In place of a natural problem context in which students can make decisions about what they want their words to mean, and what notions they wish to codify, they are instead subjected to an endless sequence of unmotivated and a priori “definitions.” The curriculum is obsessed with jargon and nomenclature, seemingly for no other purpose than to provide teachers with something to test the students on. No mathematician in the world would bother making these senseless distinctions:
21
/
2
2 1/2
21/2 is a “mixed number,” while
5
/
2
5/2
5/2 is an “improper fraction.” They’re equal for crying out loud. They are the same exact numbers, and have the same exact properties. Who uses such words outside of fourth grade?
学生本可以在自然的问题情境中,决定自己的术语要表达什么意思、想要明确哪些概念,但取而代之的是,他们要面对一连串毫无缘由、先验的“定义”。课程体系对术语和命名法异常执着,似乎唯一的目的就是给教师提供考察学生的内容。世界上没有哪个数学家会费心去做这种无意义的区分:把
21
/
2
2 1/2
21/2 叫做“带分数”,把
5
/
2
5/2
5/2 叫做“假分数”。拜托,它们是相等的!它们是完全相同的数,具有完全相同的性质。除了四年级的课堂,谁会用这些词?
Of course it is far easier to test someone’s knowledge of a pointless definition than to inspire them to create something beautiful and to find their own meaning. Even if we agree that a basic common vocabulary for mathematics is valuable, this isn’t it. How sad that fifth-graders are taught to say “quadrilateral” instead of “four-sided shape,” but are never given a reason to use words like “conjecture,” and “counterexample.” High school students must learn to use the secant function, ‘
sec
x
\sec x
secx ,’ as an abbreviation for the reciprocal of the cosine function, ‘
1
/
cos
x
1 / \cos x
1/cosx ,’ (a definition with as much intellectual weight as the decision to use ‘&’ in place of “and.” ) That this particular shorthand, a holdover from fifteenth century nautical tables, is still with us (whereas others, such as the “versine” have died out) is mere historical accident, and is of utterly no value in an era when rapid and precise shipboard computation is no longer an issue. Thus we clutter our math classes with pointless nomenclature for its own sake.
当然,考察一个人对无意义定义的掌握程度,要比激励他创造美丽的事物、找到自己的意义容易得多。即使我们认同数学需要一套基本的通用术语,也绝不是现在这种。五年级学生被教说“四边形(quadrilateral)”而不是“四条边的形状(four-sided shape)”,却从未有机会使用“猜想(conjecture)”、“反例(counterexample)”这类有意义的词汇,这多么可悲。高中生必须学习正割函数‘
sec
x
\sec x
secx ’,将其作为余弦函数倒数‘
1
/
cos
x
1 / \cos x
1/cosx ’的缩写(这个定义的智力价值,和决定用‘&’代替“and”没什么区别)。这种特定的简化符号是15世纪航海表格的遗留物,如今仍在使用(而正矢函数“versine”等其他符号已被淘汰),这纯粹是历史偶然;在船舶不再需要快速精确计算的时代,它已经毫无价值。就这样,我们的数学课被这些无意义的术语填满了。
In practice, the curriculum is not even so much a sequence of topics, or ideas, as it is a sequence of notations. Apparently mathematics consists of a secret list of mystical symbols and rules for their manipulation. Young children are given ‘
+
+
+ ’ and ‘
÷
\div
÷ .’ Only later can they be entrusted with ‘
\sqrt{}
,’ and then ‘
x
x
x ’ and ‘
y
y
y ’ and the alchemy of parentheses. Finally, they are indoctrinated in the use of ‘
sin
\sin
sin ,’ ‘
log
\log
log ,’ ‘
f
(
x
)
f(x)
f(x) ,’ and if they are deemed worthy, ‘
d
d
d ’ and ‘
∫
\int
∫ .’ All without having had a single meaningful mathematical experience.
实际上,这个课程体系与其说是一系列主题或思想的集合,不如说是一系列符号的排列。显然,在这种体系里,数学就是一份包含神秘符号和操作规则的秘密清单。小孩子先接触‘
+
+
+ ’和‘
÷
\div
÷ ’;后来才能接触‘
\sqrt{}
’;再之后是‘
x
x
x ’、‘
y
y
y ’和括号的“魔法”;最后,如果他们被认为“够格”,会被灌输‘
sin
\sin
sin ’、‘
log
\log
log ’、‘
f
(
x
)
f(x)
f(x) ’的用法,甚至‘
d
d
d ’和‘
∫
\int
∫ ’。而这一切,都是在他们没有任何一次有意义的数学体验的情况下发生的。
This program is so firmly fixed in place that teachers and textbook authors can reliably predict, years in advance, exactly what students will be doing, down to the very page of exercises. It is not at all uncommon to find second-year algebra students being asked to calculate
[
f
(
x
+
h
)
−
f
(
x
)
]
/
h
[f(x+h)-f(x)] / h
[f(x+h)−f(x)]/h for various functions
f
f
f , so that they will have “seen” this when they take calculus a few years later. Naturally no motivation is given (nor expected) for why such a seemingly random combination of operations would be of interest, although I’m sure there are many teachers who try to explain what such a thing might mean, and think they are doing their students a favor, when in fact to them it is just one more boring math problem to be gotten over with. “What do they want me to do? Oh, just plug it in? OK.”
这个课程体系固定得如此牢固,以至于教师和教科书作者能提前好几年准确预测学生要学什么,甚至精确到练习题的页码。代数二年级的学生被要求计算不同函数
f
f
f 的
[
f
(
x
+
h
)
−
f
(
x
)
]
/
h
[f(x+h)-f(x)] / h
[f(x+h)−f(x)]/h ,美其名曰让他们在几年后学微积分时“有印象”,这种情况非常普遍。当然,没有人会解释(也没人期待解释)为什么这种看似随机的运算组合会有意义——尽管我相信很多教师会试图解释它的含义,并认为这是在帮学生,但实际上,对学生来说,这只是又一道需要应付的无聊数学题。“他们想让我做什么?哦,只是代入计算?行吧。”
Another example is the training of students to express information in an unnecessarily complicated form, merely because at some distant future period it will have meaning. Does any middle school algebra teacher have the slightest clue why he is asking his students to rephrase “the number
x
x
x lies between three and seven” as
∣
x
−
5
∣
<
2
|x-5|<2
∣x−5∣<2 ? Do these hopelessly inept textbook authors really believe they are helping students by preparing them for a possible day, years hence, when they might be operating within the context of a higher-dimensional geometry or an abstract metric space? I doubt it. I expect they are simply copying each other decade after decade, maybe changing the fonts or the highlight colors, and beaming with pride when a school system adopts their book, and becomes their unwitting accomplice.
另一个例子是,训练学生用不必要的复杂形式表达信息,仅仅因为在遥远的未来,这种形式可能会有意义。有哪个初中代数老师清楚,为什么要让学生把“数
x
x
x 在 3 和 7 之间”重新表述成
∣
x
−
5
∣
<
2
|x-5|<2
∣x−5∣<2 ?这些极其无能的教科书作者,真的认为让学生为多年后可能接触的高维几何或抽象度量空间做准备,是在帮助他们吗?我对此表示怀疑。我猜他们只是在十年又十年地互相抄袭,或许改改字体或高亮颜色,然后在某个学校系统采用他们的书、无意中成为他们的帮凶时,便沾沾自喜。
Mathematics is about problems, and problems must be made the focus of a student’s mathematical life. Painful and creatively frustrating as it may be, students and their teachers should at all times be engaged in the process- having ideas, not having ideas, discovering patterns, making conjectures, constructing examples and counterexamples, devising arguments, and critiquing each other’s work. Specific techniques and methods will arise naturally out of this process, as they did historically: not isolated from, but organically connected to, and as an outgrowth of, their problem-background.
数学是关于问题的,问题必须成为学生数学学习的核心。尽管这个过程可能充满痛苦和创造性挫折,但学生和教师都应该始终投入其中——产生想法、毫无头绪、发现规律、提出猜想、构建例子与反例、设计论证、批判彼此的工作。特定的技巧和方法会从这个过程中自然产生,就像它们在历史上那样:不是孤立存在的,而是与问题背景有机相连、作为其产物而出现的。
English teachers know that spelling and pronunciation are best learned in a context of reading and writing. History teachers know that names and dates are uninteresting when removed from the unfolding backstory of events. Why does mathematics education remain stuck in the nineteenth century? Compare your own experience of learning algebra with Bertrand Russell’s recollection:
英语教师知道,拼写和发音在读写语境中学习效果最好。历史教师知道,脱离事件发展的背景故事,人名和日期会变得毫无趣味。为什么数学教育还停留在19世纪?把你自己学习代数的经历,和伯特兰·罗素的回忆对比一下:
“I was made to learn by heart: ‘The square of the sum of two numbers is equal to the sum of their squares increased by twice their product.’ I had not the vaguest idea what this meant and when I could not remember the words, my tutor threw the book at my head, which did not stimulate my intellect in any way.”
“我被迫背诵:‘两个数的和的平方,等于它们的平方和加上它们乘积的两倍。’我完全不知道这是什么意思,当我记不住这句话时,我的导师就把书扔到我头上,这对我的智力毫无启发。”
Are things really any different today?
如今的情况真的有任何不同吗?
SIMPLICIO: I don’t think that’s very fair. Surely teaching methods have improved since then.
辛普利西奥:我觉得这不太公平。从那以后,教学方法肯定已经改进了。
SALVIATI:
You mean training methods. Teaching is a messy human relationship; it does not require a method. Or rather I should say, if you need a method you’re probably not a very good teacher. If you don’t have enough of a feeling for your subject to be able to talk about it in your own voice, in a natural and spontaneous way, how well could you understand it? And speaking of being stuck in the nineteenth century, isn’t it shocking how the curriculum itself is stuck in the seventeenth? To think of all the amazing discoveries and profound revolutions in mathematical thought that have occurred in the last three centuries! There is no more mention of these than if they had never happened.
萨尔维亚蒂:
你说的是“训练方法”。教学是一种复杂的人际互动,不需要什么“方法”。或者更准确地说,如果你需要靠“方法”教学,那你可能不是一个好老师。如果你对你的学科没有足够的感悟,无法用自己的声音、自然自发地谈论它,那你对它的理解能有多深?说到停留在19世纪,课程体系本身停留在17世纪,难道不更令人震惊吗?想想过去三个世纪里,数学思想领域出现了多少惊人的发现和深刻的变革!但课程体系对这些内容的提及,就好像它们从未发生过一样。
SIMPLICIO:
But aren’t you asking an awful lot from our math teachers? You expect them to provide individual attention to dozens of students, guiding them on their own paths toward discovery and enlightenment, and to be up on recent mathematical history as well?
辛普利西奥:
但你对我们的数学教师要求是不是太高了?你期望他们给几十个学生提供个性化关注,引导他们沿着各自的路径去发现和领悟,同时还要了解最新的数学史?
SALVIATI:
Do you expect your art teacher to be able to give you individualized, knowledgeable advice about your painting? Do you expect her to know anything about the last three hundred years of art history? But seriously, I don’t expect anything of the kind, I only wish it were so.
萨尔维亚蒂:
你难道不期望你的美术老师能就你的画作,给出个性化、有见识的建议吗?你不期望她了解过去三百年的艺术史吗?但说真的,我并没有期望数学教师能做到这些,我只是希望情况能如此。
SIMPLICIO:
So you blame the math teachers?
辛普利西奥:
所以你在责怪数学教师?
SALVIATI:
No, I blame the culture that produces them. The poor devils are trying their best, and are only doing what they’ve been trained to do. I’m sure most of them love their students and hate what they are being forced to put them through. They know in their hearts that it is meaningless and degrading. They can sense that they have been made cogs in a great soul-crushing machine, but they lack the perspective needed to understand it, or to fight against it. They only know they have to get the students “ready for next year.”
萨尔维亚蒂:
不,我责怪的是培养他们的文化。这些可怜的人已经在尽最大努力了,他们只是在做自己被训练去做的事。我相信他们大多数人都爱自己的学生,也痛恨自己被迫让学生经历这些。他们内心深处知道这一切是无意义且有辱人格的。他们能感觉到自己成了一台摧残心灵的巨大机器上的齿轮,却缺乏理解或反抗这台机器所需的视角。他们只知道,必须让学生“为明年做好准备”。
SIMPLICIO:
Do you really think that most students are capable of operating on such a high level as to create their own mathematics?
辛普利西奥:
你真的认为大多数学生都能达到自己创造数学的高水平吗?
SALVIATI:
If we honestly believe that creative reasoning is too “high” for our students, and that they can’t handle it, why do we allow them to write history papers or essays about Shakespeare? The problem is not that the students can’t handle it, it’s that none of the teachers can. They’ve never proved anything themselves, so how could they possibly advise a student? In any case, there would obviously be a range of student interest and ability, as there is in any subject, but at least students would like or dislike mathematics for what it really is, and not for this perverse mockery of it.
萨尔维亚蒂:
如果我们真的认为创造性推理对学生来说太“高深”,他们无法应对,那为什么我们允许他们写历史论文或关于莎士比亚的文章呢?问题不在于学生无法应对,而在于教师们都做不到。他们自己从未证明过任何东西,怎么可能给学生提供建议?无论如何,和任何学科一样,学生的兴趣和能力显然会有差异,但至少学生喜欢或讨厌数学,是因为数学本身,而不是因为这种对数学的扭曲模仿。
SIMPLICIO:
But surely we want all of our students to learn a basic set of facts and skills. That’s what a curriculum is for, and that’s why it is so uniform- there are certain timeless, cold hard facts we need our students to know: one plus one is two, and the angles of a triangle add up to 180 degrees. These are not opinions, or mushy artistic feelings.
辛普利西奥:
但我们肯定希望所有学生都学到一套基本的事实和技能。这就是课程体系的目的,也是它如此统一的原因——有些永恒、确凿的事实,我们需要学生了解:1加1等于2,三角形的内角和是180度。这些不是观点,也不是模糊的艺术感受。
SALVIATI:
On the contrary. Mathematical structures, useful or not, are invented and developed within a problem context, and derive their meaning from that context. Sometimes we want one plus one to equal zero (as in so-called ‘mod 2’ arithmetic) and on the surface of a sphere the angles of a triangle add up to more than 180 degrees. There are no “facts” per se; everything is relative and relational. It is the story that matters, not just the ending.
萨尔维亚蒂:
恰恰相反。无论是否有用,数学结构都是在问题情境中被发明和发展的,其意义也源于这个情境。有时候,我们会让1加1等于0(比如在所谓的“模2算术”中);而在球面上,三角形的内角和会大于180度。根本不存在所谓的“绝对事实”,一切都是相对的、相关的。重要的是过程和背景,而不仅仅是结果。
SIMPLICIO:
I’m getting tired of all your mystical mumbo-jumbo! Basic arithmetic, all right? Do you or do you not agree that students should learn it?
辛普利西奥:
我已经听腻了你这些神秘的胡言乱语!就说基础算术,好吗?你到底同不同意学生应该学基础算术?
SALVIATI:
That depends on what you mean by “it.” If you mean having an appreciation for the problems of counting and arranging, the advantages of grouping and naming, the distinction between a representation and the thing itself, and some idea of the historical development of number systems, then yes, I do think our students should be exposed to such things. If you mean the rote memorization of arithmetic facts without any underlying conceptual framework, then no. If you mean exploring the not at all obvious fact that five groups of seven is the same as seven groups of five, then yes. If you mean making a rule that
5
×
7
=
7
×
5
5 ×7=7 ×5
5×7=7×5 , then no. Doing mathematics should always mean discovering patterns and crafting beautiful and meaningful explanations.
萨尔维亚蒂:
这取决于你说的“基础算术”是什么意思。如果你指的是理解计数和排列的问题、分组和命名的优势、符号与事物本身的区别,以及对数字系统历史发展的一些了解,那么是的,我认为学生应该接触这些内容。如果你指的是在没有任何底层概念框架的情况下,死记硬背算术事实,那么不。如果你指的是探索“5个7相加”和“7个5相加”相等这个并非显而易见的事实,那么是的。如果你指的是制定一条“
5
×
7
=
7
×
5
5 ×7=7 ×5
5×7=7×5 ”的规则,那么不。做数学,永远应该意味着发现规律,并构建优美且有意义的解释。
SIMPLICIO:
What about geometry? Don’t students prove things there? Isn’t High School Geometry a perfect example of what you want math classes to be?
辛普利西奥:
那几何呢?学生不是在几何课上证明东西吗?高中几何难道不是你理想中数学课的完美例子吗?
High School Geometry: Instrument of the Devil
高中几何:魔鬼的工具
There is nothing quite so vexing to the author of a scathing indictment as having the primary target of his venom offered up in his support. And never was a wolf in sheep’s clothing as insidious, nor a false friend as treacherous, as High School Geometry. It is precisely because it is school’s attempt to introduce students to the art of argument that makes it so very dangerous.
对于一篇尖锐控诉文的作者来说,最令人恼火的莫过于自己主要抨击的对象,反而被当作支持自己观点的例子。而高中几何,就是这样一只披着羊皮、阴险狡诈的狼,一个背信弃义的假朋友。正是因为它试图向学生介绍论证的艺术,才使得它如此危险。
Posing as the arena in which students will finally get to engage in true mathematical reasoning, this virus attacks mathematics at its heart, destroying the very essence of creative rational argument, poisoning the students’ enjoyment of this fascinating and beautiful subject, and permanently disabling them from thinking about math in a natural and intuitive way.
它伪装成一个让学生终于能进行真正数学推理的舞台,却像病毒一样攻击数学的核心,摧毁创造性理性论证的本质,扼杀学生对这门迷人而美丽学科的热爱,并永久地让他们无法以自然、直观的方式思考数学。
The mechanism behind this is subtle and devious. The student-victim is first stunned and paralyzed by an onslaught of pointless definitions, propositions, and notations, and is then slowly and painstakingly weaned away from any natural curiosity or intuition about shapes and their patterns by a systematic indoctrination into the stilted language and artificial format of so-called “formal geometric proof.”
这背后的机制微妙而阴险。受害的学生首先被大量无意义的定义、命题和符号冲击得不知所措,然后通过系统灌输所谓“正式几何证明”的生硬语言和人为格式,逐渐、痛苦地失去对形状及其规律的自然好奇心和直觉。
All metaphor aside, geometry class is by far the most mentally and emotionally destructive component of the entire K-12 mathematics curriculum. Other math courses may hide the beautiful bird, or put it in a cage, but in geometry class it is openly and cruelly tortured. (Apparently I am incapable of putting all metaphor aside.)
抛开所有比喻不谈,几何课是整个K-12数学课程体系中,对学生心智和情感最具破坏性的部分。其他数学课程可能只是把美丽的鸟儿藏起来,或者关进笼子,但在几何课上,这只鸟被公然、残忍地折磨。(显然,我还是忍不住要用比喻。)
What is happening is the systematic undermining of the student’s intuition. A proof, that is, a mathematical argument, is a work of fiction, a poem. Its goal is to satisfy. A beautiful proof should explain, and it should explain clearly, deeply, and elegantly. A well-written, well-crafted argument should feel like a splash of cool water, and be a beacon of light— it should refresh the spirit and illuminate the mind. And it should be charming.
实际发生的事情,是对学生直觉的系统性破坏。证明,也就是数学论证,是一部虚构作品,一首诗。它的目标是让人信服。一个优美的证明应该能解释问题,而且解释得清晰、深刻、优雅。一篇写得好、构思精妙的论证,应该像一阵清凉的水花,像一盏明灯——它能振奋精神,启迪心灵,而且应该富有魅力。
There is nothing charming about what passes for proof in geometry class. Students are presented a rigid and dogmatic format in which their so-called “proofs” are to be conducted— a format as unnecessary and inappropriate as insisting that children who wish to plant a garden refer to their flowers by genus and species.
几何课上所谓的“证明”,毫无魅力可言。学生们被要求用一种僵化、教条的格式来完成他们的“证明”——这种格式的不必要和不合时宜,就好比强迫想种花的孩子用属名和种名来称呼他们的花。
Let’s look at some specific instances of this insanity. We’ll begin with the example of two crossed lines:
让我们看看这种荒谬的具体例子。先从两条相交的直线说起:
Now the first thing that usually happens is the unnecessary muddying of the waters with excessive notation. Apparently, one cannot simply speak of two crossed lines; one must give elaborate names to them. And not simple names like ‘line 1’ and ‘line 2,’ or even ‘
a
a
a and
b
b
b . We must (according to High School Geometry) select random and irrelevant points on these lines, and then refer to the lines using the special “line notation.”
通常首先发生的,就是用过多的符号进行不必要的混淆。显然,你不能简单地说“两条相交的直线”,必须给它们起复杂的名字。而且不能是“直线1”“直线2”这种简单的名字,甚至不能是“
a
a
a ”和“
b
b
b ”。根据高中几何的要求,我们必须在这些直线上随机选取无关的点,然后用特殊的“直线符号”来指代这些直线。
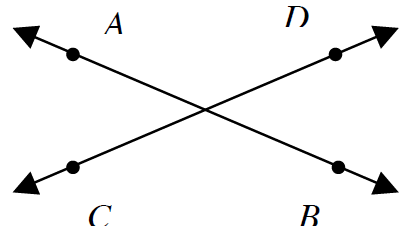
(图注:直线上标记的点依次为 A、D 和 C、B)
You see, now we get to call them
A
B
AB
AB and
C
D
CD
CD . And God forbid you should omit the little bars on top— ‘
A
B
AB
AB ’ refers to the length of the line
A
B
AB
AB (at least I think that’s how it works). Never mind how pointlessly complicated it is, this is the way one must learn to do it. Now comes the actual statement, usually referred to by some absurd name like
你看,现在我们要把它们叫做
A
B
AB
AB 和
C
D
CD
CD 了。而且千万不能漏掉上方的小横线——“
A
B
AB
AB ”指的是直线
A
B
AB
AB 的长度(至少我认为是这样)。别管这有多没必要、多复杂,你必须学会这么做。接下来是正式的命题,通常会被赋予一个荒唐的名称,比如:
PROPOSITION 2.1.1.
命题 2.1.1
Let
A
B
ˉ
\bar{AB}
ABˉ and
C
D
ˉ
\bar{CD}
CDˉ intersect at
P
P
P . Then
∠
A
P
C
≅
∠
B
P
D
\angle APC \cong \angle BPD
∠APC≅∠BPD .
设直线
A
B
ˉ
\bar{AB}
ABˉ 与直线
C
D
ˉ
\bar{CD}
CDˉ 相交于点
P
P
P ,则
∠
A
P
C
≅
∠
B
P
D
\angle APC \cong \angle BPD
∠APC≅∠BPD 。
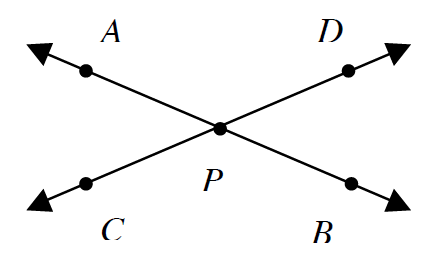
(图注:点 P 为两条直线交点,连接后形成角 ∠ A P C \angle APC ∠APC 和 ∠ B P D \angle BPD ∠BPD )
In other words, the angles on both sides are the same. Well, duh! The configuration of two crossed lines is symmetrical for crissake. And as if this wasn’t bad enough, this patently obvious statement about lines and angles must then be “proved.”
换句话说,就是对顶角相等。拜托,这不是明摆着的吗!两条直线相交的结构,本身就是对称的啊。而更糟糕的是,这个关于直线和角的、显而易见的结论,还必须被“证明”。
| Statement | Reason |
|---|---|
| 1.
m
∠
A
P
C
+
m
∠
A
P
D
=
180
m \angle APC + m \angle APD = 180
m∠APC+m∠APD=180 ; m ∠ B P D + m ∠ A P D = 180 m \angle BPD + m \angle APD = 180 m∠BPD+m∠APD=180 | 1. Angle Addition Postulate 角的和公理 |
| 2. m ∠ A P C + m ∠ A P D = m ∠ B P D + m ∠ A P D m \angle APC + m \angle APD = m \angle BPD + m \angle APD m∠APC+m∠APD=m∠BPD+m∠APD | 2. Substitution Property 等量代换性质 |
| 3. m ∠ A P D = m ∠ A P D m \angle APD = m \angle APD m∠APD=m∠APD | 3. Reflexive Property of Equality 等式的自反性 |
| 4. m ∠ A P C = m ∠ B P D m \angle APC = m \angle BPD m∠APC=m∠BPD | 4. Subtraction Property of Equality 等式的减法性质 |
| 5. ∠ A P C ≅ ∠ B P D \angle APC \cong \angle BPD ∠APC≅∠BPD | 5. Angle Measurement Postulate 角度测量公理 |
Instead of a witty and enjoyable argument written by an actual human being, and conducted in one of the world’s many natural languages, we get this sullen, soulless, bureaucratic form-letter of a proof. And what a mountain being made of a molehill! Do we really want to suggest that a straightforward observation like this requires such an extensive preamble? Be honest: did you actually even read it? Of course not. Who would want to?
我们没有得到一个由真人用某种自然语言写出的、机智有趣的论证,反而得到了一个沉闷、无灵魂、像官方公函一样的证明格式。这简直是小题大做!我们真的要暗示,这样一个简单直接的观察结果,需要如此繁琐的证明过程吗?说实话,你真的看完这个证明了吗?当然没有,谁会愿意看呢?
The effect of such a production being made over something so simple is to make people doubt their own intuition. Calling into question the obvious, by insisting that it be “rigorously proved” (as if the above even constitutes a legitimate formal proof) is to say to a student, “Your feelings and ideas are suspect. You need to think and speak our way.”
对如此简单的事情大费周章,只会让人们怀疑自己的直觉。通过坚持让“显而易见的结论”被“严格证明”(仿佛上面的过程能算得上合法的正式证明),来质疑显而易见的事实,这无异于对学生说:“你的感受和想法是不可信的。你必须按照我们的方式思考和表达。”
Now there is a place for formal proof in mathematics, no question. But that place is not a student’s first introduction to mathematical argument. At least let people get familiar with some mathematical objects, and learn what to expect from them, before you start formalizing everything. Rigorous formal proof only becomes important when there is a crisis— when you discover that your imaginary objects behave in a counterintuitive way; when there is a paradox of some kind. But such excessive preventative hygiene is completely unnecessary here— nobody’s gotten sick yet! Of course if a logical crisis should arise at some point, then obviously it should be investigated, and the argument made more clear, but that process can be carried out intuitively and informally as well. In fact it is the soul of mathematics to carry out such a dialogue with one’s own proof.
毫无疑问,数学中确实有正式证明的一席之地。但这个位置绝不是学生初次接触数学论证的地方。至少应该让人们先熟悉一些数学对象,了解它们的特性,然后再开始将一切形式化。只有当出现“危机”时——比如发现你想象中的对象表现出反直觉的行为,或者出现某种悖论时——严格的正式证明才变得重要。但在这里,这种过度的“预防性严谨”完全没有必要——还没有人因为直觉出错而“受害”呢!当然,如果在某个时候出现了逻辑危机,那显然需要调查,并让论证更清晰,但这个过程也可以通过直观、非正式的方式进行。事实上,与自己的证明进行这样的对话,正是数学的灵魂所在。
So not only are most kids utterly confused by this pedantry— nothing is more mystifying than a proof of the obvious— but even those few whose intuition remains intact must then retranslate their excellent, beautiful ideas back into this absurd hieroglyphic framework in order for their teacher to call it “correct.” The teacher then flatters himself that he is somehow sharpening his students’ minds.
因此,大多数孩子不仅被这种迂腐的做法弄得完全困惑——没有什么比证明显而易见的事情更令人困惑的了——而且即使是那些直觉仍未受损的少数学生,也必须将自己优秀、优美的想法重新翻译成这种荒谬的“象形文字”框架,才能让老师认为是“正确的”。然后老师还自鸣得意,认为自己在某种程度上提升了学生的思维能力。
As a more serious example, let’s take the case of a triangle inside a semicircle:
再举一个更典型的例子,看看半圆内接三角形的情况:
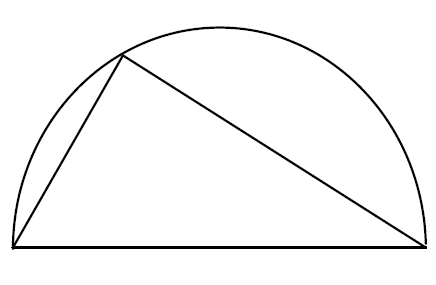
Now the beautiful truth about this pattern is that no matter where on the circle you place the tip of the triangle, it always forms a nice right angle. (I have no objection to a term like “right angle” if it is relevant to the problem and makes it easier to discuss. It’s not terminology itself that I object to, it’s pointless unnecessary terminology. In any case, I would be happy to use “corner” or even “pigpen” if a student preferred.)
这个图形的美丽真相是:无论你把三角形的顶点放在圆上的哪个位置,这个角始终是一个直角。(如果“直角”这个术语与问题相关,且能让讨论更轻松,我并不反对使用它。我反对的不是术语本身,而是无意义、不必要的术语。无论如何,如果学生愿意,我很乐意用“角(corner)”甚至“猪圈(pigpen)”这样的词来称呼它。)
Here is a case where our intuition is somewhat in doubt. It’s not at all clear that this should be true; it even seems unlikely— shouldn’t the angle change if I move the tip? What we have here is a fantastic math problem! Is it true? If so, why is it true? What a great project! What a terrific opportunity to exercise one’s ingenuity and imagination! Of course no such opportunity is given to the students, whose curiosity and interest is immediately deflated by:
这是一个我们的直觉会受到挑战的例子。这个结论并非显而易见,甚至看起来不太可能——移动顶点的位置,角的大小难道不会变吗?这本身就是一个绝妙的数学问题!结论是真的吗?如果是,为什么是真的?多么棒的探索项目!多么好的锻炼创造力和想象力的机会!当然,学生们永远得不到这样的机会,他们的好奇心和兴趣会立刻被下面的内容浇灭:
THEOREM 9.5. Let
△
A
B
C
\triangle ABC
△ABC be inscribed in a semicircle with diameter
A
C
ˉ
\bar{AC}
ACˉ. Then
∠
A
B
C
\angle ABC
∠ABC is a right angle.
定理 9.5 设
△
A
B
C
\triangle ABC
△ABC 内接于以
A
C
ˉ
\bar{AC}
ACˉ 为直径的半圆,则
∠
A
B
C
\angle ABC
∠ABC 为直角。
(图注:点 O 为半圆的圆心, A C AC AC 为直径,点 B 在半圆上,构成 △ A B C \triangle ABC △ABC )
| Statement (陈述) | Reason (依据) |
|---|---|
| 1. Draw radius O B OB OB. Then O B = O C = O A OB = OC = OA OB=OC=OA | 1. Given (radii of the same circle are equal) 已知条件(同圆半径相等) |
| 2. m ∠ O B C = m ∠ B C A m\angle OBC = m\angle BCA m∠OBC=m∠BCA; m ∠ O B A = m ∠ B A C m\angle OBA = m\angle BAC m∠OBA=m∠BAC | 2. Isosceles Triangle Theorem 等腰三角形定理 |
| 3. m ∠ A B C = m ∠ O B A + m ∠ O B C m\angle ABC = m\angle OBA + m\angle OBC m∠ABC=m∠OBA+m∠OBC | 3. Angle Sum Postulate 角的和公理 |
| 4. m ∠ A B C + m ∠ B C A + m ∠ B A C = 18 0 ∘ m\angle ABC + m\angle BCA + m\angle BAC = 180^\circ m∠ABC+m∠BCA+m∠BAC=180∘ | 4. The sum of the interior angles of a triangle is
18
0
∘
180^\circ
180∘ 三角形内角和为 18 0 ∘ 180^\circ 180∘ |
| 5. m ∠ A B C + m ∠ O B C + m ∠ O B A = 18 0 ∘ m\angle ABC + m\angle OBC + m\angle OBA = 180^\circ m∠ABC+m∠OBC+m∠OBA=180∘ | 5. Substitution (from Step 2) 代入(由步骤 2 可得) |
| 6. 2 m ∠ A B C = 18 0 ∘ 2m\angle ABC = 180^\circ 2m∠ABC=180∘ | 6. Substitution (from Step 3) 代入(由步骤 3 可得) |
| 7. m ∠ A B C = 9 0 ∘ m\angle ABC = 90^\circ m∠ABC=90∘ | 7. Division Property of Equality 等式的除法性质 |
| 8. ∠ A B C \angle ABC ∠ABC is a right angle | 8. Definition of a Right Angle 直角的定义 |
Could anything be more unattractive and inelegant? Could any argument be more obfuscatory and unreadable? This isn’t mathematics! A proof should be an epiphany from the Gods, not a coded message from the Pentagon. This is what comes from a misplaced sense of logical rigor: ugliness. The spirit of the argument has been buried under a heap of confusing formalism.
还有比这更乏味、更不雅的吗?还有比这更晦涩、更难读的论证吗?这根本不是数学!一个证明应该像来自神明的顿悟,而不是来自五角大楼的加密信息。这种错位的逻辑严谨性,只会产生丑陋的结果。论证的精髓被一堆令人困惑的形式主义所掩盖。
No mathematician works this way. No mathematician has ever worked this way. This is a complete and utter misunderstanding of the mathematical enterprise. Mathematics is not about erecting barriers between ourselves and our intuition, and making simple things complicated. Mathematics is about removing obstacles to our intuition, and keeping simple things simple.
没有哪个数学家是这样工作的。从来没有。这是对数学事业完全彻底的误解。数学不是要在我们和直觉之间建立障碍,把简单的事情变复杂。数学是要清除直觉的障碍,让简单的事情保持简单。
Compare this unappetizing mess of a proof with the following argument devised by one of my seventh-graders:
把这堆令人倒胃口的证明,和我教过的一个七年级学生想出的论证对比一下:
“Take the triangle and rotate it around so it makes a four-sided box inside the circle. Since the triangle got turned completely around, the sides of the box must be parallel, so it makes a parallelogram. But it can’t be a slanted box because both of its diagonals are diameters of the circle, so they’re equal, which means it must be an actual rectangle. That’s why the corner is always a right angle.”
“把这个三角形旋转一下,让它在圆里面形成一个四边形。因为三角形完全转了一圈,所以这个四边形的对边肯定是平行的,那它就是一个平行四边形。但它不可能是斜的,因为它的两条对角线都是圆的直径,长度相等,所以它肯定是一个长方形。这就是为什么那个角总是直角了。”
Isn’t that just delightful? And the point isn’t whether this argument is any better than the other one as an idea, the point is that the idea comes across. (As a matter of fact, the idea of the first proof is quite pretty, albeit seen as through a glass, darkly.)
这难道不令人愉快吗?重点不在于这个论证的想法是否比前一个更好,而在于这个想法被清晰地表达出来了。(事实上,第一个证明的想法本身其实很优美,只是被形式主义弄得晦涩难懂。)
More importantly, the idea was the student’s own. The class had a nice problem to work on, conjectures were made, proofs were attempted, and this is what one student came up with. Of course it took several days, and was the end result of a long sequence of failures.
更重要的是,这个想法是学生自己的。全班同学共同研究一个有趣的问题,提出猜想,尝试证明,而这就是其中一个学生的成果。当然,这个过程花了好几天,而且是在一系列失败之后才得到的结果。
To be fair, I did paraphrase the proof considerably. The original was quite a bit more convoluted, and contained a lot of unnecessary verbiage (as well as spelling and grammatical errors). But I think I got the feeling of it across. And these defects were all to the good; they gave me something to do as a teacher. I was able to point out several stylistic and logical problems, and the student was then able to improve the argument. For instance, I wasn’t completely happy with the bit about both diagonals being diameters— I didn’t think that was entirely obvious— but that only meant there was more to think about and more understanding to be gained from the situation. And in fact the student was able to fill in this gap quite nicely:
公平地说,我对这个证明做了大量转述。学生最初的表述要复杂得多,包含很多不必要的废话(还有拼写和语法错误)。但我认为我传达出了它的核心思路。而这些缺陷反而是好事:它们给了我作为教师可以发挥的空间。我能指出其中的一些表达和逻辑问题,然后学生就能改进自己的论证。比如,我对“两条对角线都是直径”这一点并不完全满意——我认为这并非完全显而易见——但这恰恰意味着还有更多值得思考的地方,能让人从中获得更深的理解。事实上,学生后来很好地填补了这个漏洞:
“Since the triangle got rotated halfway around the circle, the tip must end up exactly opposite from where it started. That’s why the diagonal of the box is a diameter.”
“因为三角形绕着圆转了半圈,所以它的顶点最后会落在和起点正对面的位置。这就是为什么那个四边形的对角线是直径。”
So a great project and a beautiful piece of mathematics. I’m not sure who was more proud, the student or myself. This is exactly the kind of experience I want my students to have.
这真是一个很棒的探索项目,也是一段优美的数学思考。我不知道是学生更自豪,还是我更自豪。这正是我希望我的学生拥有的学习体验。
The problem with the standard geometry curriculum is that the private, personal experience of being a struggling artist has virtually been eliminated. The art of proof has been replaced by a rigid step-by step pattern of uninspired formal deductions. The textbook presents a set of definitions, theorems, and proofs, the teacher copies them onto the blackboard, and the students copy them into their notebooks. They are then asked to mimic them in the exercises. Those that catch on to the pattern quickly are the “good” students.
标准几何课程的问题在于,它几乎完全剥夺了学生作为“努力探索的创作者”的个人体验。证明的艺术,被一套僵化、毫无灵感的正式演绎步骤所取代。教科书呈现出一套定义、定理和证明,教师把它们抄到黑板上,学生再抄到笔记本里。然后学生被要求在练习题中模仿这些步骤。那些能快速掌握这种模式的学生,就被视为“好学生”。
The result is that the student becomes a passive participant in the creative act. Students are making statements to fit a preexisting proof-pattern, not because they mean them. They are being trained to ape arguments, not to intend them. So not only do they have no idea what their teacher is saying, they have no idea what they themselves are saying.
结果就是,学生在创造性活动中变成了被动的参与者。学生做出陈述,是为了迎合预设的证明模式,而不是因为他们真正理解这些陈述的含义。他们被训练去模仿论证,而不是去理解和构建论证。因此,他们不仅不知道老师在说什么,也不知道自己在说什么。
Even the traditional way in which definitions are presented is a lie. In an effort to create an illusion of “clarity” before embarking on the typical cascade of propositions and theorems, a set of definitions are provided so that statements and their proofs can be made as succinct as possible. On the surface this seems fairly innocuous; why not make some abbreviations so that things can be said more economically? The problem is that definitions matter. They come from aesthetic decisions about what distinctions you as an artist consider important. And they are problem-generated. To make a definition is to highlight and call attention to a feature or structural property. Historically this comes out of working on a problem, not as a prelude to it.
甚至连传统的定义呈现方式都是一种误导。在开始一连串典型的命题和定理之前,为了营造一种“清晰”的假象,课程会先提供一套定义,以便让陈述和证明尽可能简洁。表面上看,这似乎没什么问题——为什么不创造一些缩写,让表达更简洁呢?问题在于,定义是有意义的。它们源于你作为“创作者”对“哪些区别重要”的审美判断,而且是由问题催生的。下定义,是为了强调和关注某个特征或结构属性。从历史上看,定义是在研究问题的过程中产生的,而不是作为研究问题的前奏。
The point is you don’t start with definitions, you start with problems. Nobody ever had an idea of a number being “irrational” until Pythagoras attempted to measure the diagonal of a square and discovered that it could not be represented as a fraction. Definitions make sense when a point is reached in your argument which makes the distinction necessary. To make definitions without motivation is more likely to cause confusion.
关键在于,你不能从定义开始,而应该从问题开始。在毕达哥拉斯试图测量正方形的对角线,并发现它无法用分数表示之前,没有人会想到“无理数”这个概念。只有当你的论证进行到某个需要区分的节点时,定义才有意义。毫无缘由地给出定义,更可能造成困惑。
This is yet another example of the way that students are shielded and excluded from the mathematical process. Students need to be able to make their own definitions as the need arises— to frame the debate themselves. I don’t want students saying, “the definition, the theorem, the proof,” I want them saying, “my definition, my theorem, my proof.”
这又是一个学生被屏蔽在数学过程之外的例子。学生需要能够在需要时自己下定义——自己构建讨论的框架。我不希望学生说“这个定义、这个定理、这个证明”,我希望他们说“我的定义、我的定理、我的证明”。
All of these complaints aside, the real problem with this kind of presentation is that it is boring. Efficiency and economy simply do not make good pedagogy. I have a hard time believing that Euclid would approve of this; I know Archimedes wouldn’t.
抛开所有这些抱怨不谈,这种呈现方式的真正问题在于它太无聊了。高效和简洁绝不是好的教学方法。我很难相信欧几里得会认可这种方式;而阿基米德肯定不会。
SIMPLICIO:
Now hold on a minute. I don’t know about you, but I actually enjoyed my high school geometry class. I liked the structure, and I enjoyed working within the rigid proof format.
辛普利西奥:
等一下。我不知道你的情况,但我其实很喜欢我的高中几何课。我喜欢它的结构,也喜欢在僵化的证明格式里做题。
SALVIATI:
I’m sure you did. You probably even got to work on some nice problems occasionally. Lot’s of people enjoy geometry class (although lots more hate it). But this is not a point in favor of the current regime. Rather, it is powerful testimony to the allure of mathematics itself. It’s hard to completely ruin something so beautiful; even this faint shadow of mathematics can still be engaging and satisfying. Many people enjoy paint-by-numbers as well; it is a relaxing and colorful manual activity. That doesn’t make it the real thing, though.
萨尔维亚蒂:
我相信你说的是真的。你可能偶尔还会遇到一些有趣的问题。很多人喜欢几何课(尽管更多人讨厌它)。但这并不能成为支持现行体系的理由,反而恰恰证明了数学本身的魅力。要彻底毁掉如此美丽的东西是很难的;即使是数学的微弱影子,也依然能吸引人并带来满足感。很多人也喜欢数字填色画,这是一种轻松、色彩丰富的手工活动,但这并不意味着它就是真正的绘画艺术。
SIMPLICIO:
But I’m telling you, I liked it.
辛普利西奥:
但我就是喜欢它。
SALVIATI:
And if you had had a more natural mathematical experience you would have liked it even more.
萨尔维亚蒂:
如果你能有更自然的数学学习体验,你会更喜欢数学本身的。
SIMPLICIO:
So we’re supposed to just set off on some free-form mathematical excursion, and the students will learn whatever they happen to learn?
辛普利西奥:
所以你的意思是,我们应该进行一些自由形式的数学探索,学生学到什么算什么?
SALVIATI:
Precisely. Problems will lead to other problems, technique will be developed as it becomes necessary, and new topics will arise naturally. And if some issue never happens to come up in thirteen years of schooling, how interesting or important could it be?
萨尔维亚蒂:
正是如此。一个问题会引出另一个问题,技巧会在需要时自然发展出来,新的主题也会自然出现。如果某个内容在13年的学校教育中从未出现过,那它能有多有趣、多重要呢?
SIMPLICIO:
You’ve gone completely mad.
辛普利西奥:
你简直是疯了。
SALVIATI:
Perhaps I have. But even working within the conventional framework a good teacher can guide the discussion and the flow of problems so as to allow the students to discover and invent mathematics for themselves. The real problem is that the bureaucracy does not allow an individual teacher to do that. With a set curriculum to follow, a teacher cannot lead. There should be no standards, and no curriculum. Just individuals doing what they think best for their students.
萨尔维亚蒂:
也许我是疯了。但即使在传统框架内,一个好的教师也能引导讨论和问题的走向,让学生自己发现和创造数学。真正的问题在于,教育官僚体系不允许教师这样做。有了固定的课程体系要遵循,教师就无法引领学生。我们不应该有统一的标准和课程,而应该让每个教育者做他们认为对学生最好的事情。
SIMPLICIO:
But then how can schools guarantee that their students will all have the same basic knowledge? How will we accurately measure their relative worth?
辛普利西奥:
但那样的话,学校如何保证所有学生都掌握相同的基础知识?我们如何准确衡量他们的相对能力?
SALVIATI:
They can’t, and we won’t. Just like in real life. Ultimately you have to face the fact that people are all different, and that’s just fine. In any case, there’s no urgency. So a person graduates from high school not knowing the half-angle formulas (as if they do now!) So what? At least that person would come away with some sort of an idea of what the subject is really about, and would get to see something beautiful.
萨尔维亚蒂:
学校无法保证,我们也无需衡量。就像在现实生活中一样。最终你必须接受一个事实:人都是不同的,而这没什么不好。无论如何,这并不紧急。就算一个人高中毕业时不知道半角公式(好像现在的学生真的知道似的!),那又怎样?至少他会对数学这门学科的本质有所了解,能看到它美丽的一面。
In Conclusion…
结语
To put the finishing touches on my critique of the standard curriculum, and as a service to the community, I now present the first ever completely honest course catalog for K-12 mathematics:
为了给我对标准课程体系的批判画上句号,也为了给大家提供参考,我现在呈现出第一份完全诚实的K-12数学课程目录:
The Standard School Mathematics Curriculum
标准学校数学课程体系
LOWER SCHOOL MATH
小学低年级数学
The indoctrination begins. Students learn that mathematics is not something you do, but something that is done to you. Emphasis is placed on sitting still, filling out worksheets, and following directions. Children are expected to master a complex set of algorithms for manipulating Hindi symbols, unrelated to any real desire or curiosity on their part, and regarded only a few centuries ago as too difficult for the average adult. Multiplication tables are stressed, as are parents, teachers, and the kids themselves.
灌输开始了。学生们学到:数学不是你主动去“做”的东西,而是别人强加给你的东西。重点是安静坐着、填练习题、听从指令。孩子们需要掌握一套复杂的算法,用来操作阿拉伯数字符号——这与他们自身的真实渴望或好奇心毫无关系,而仅仅在几个世纪前,这些算法还被认为对普通成年人来说太难了。乘法表被反复强调,家长、教师和孩子自己也因此备受压力。
MIDDLE SCHOOL MATH
初中数学
Students are taught to view mathematics as a set of procedures, akin to religious rites, which are eternal and set in stone. The holy tablets, or “Math Books,” are handed out, and the students learn to address the church elders as “they” (as in “What do they want here? Do they want me to divide?”) Contrived and artificial “word problems” will be introduced in order to make the mindless drudgery of arithmetic seem enjoyable by comparison. Students will be tested on a wide array of unnecessary technical terms, such as ‘whole number’ and ‘proper fraction,’ without the slightest rationale for making such distinctions. Excellent preparation for Algebra I.
学生们被教导将数学视为一套类似宗教仪式的流程,永恒不变、不可更改。“圣典”(即“数学课本”)被分发下来,学生们学会将课程制定者称为“他们”(比如“他们想让我在这里做什么?要我做除法吗?”)。为了让枯燥的算术显得没那么难熬,课程会引入刻意编造的“应用题”。学生还会被考察大量不必要的专业术语,比如“整数(whole number)”和“真分数(proper fraction)”,但这些区分毫无合理依据。这是为代数 I 做的“绝佳”准备。
ALGEBRA I
代数 I
So as not to waste valuable time thinking about numbers and their patterns, this course instead focuses on symbols and rules for their manipulation. The smooth narrative thread that leads from ancient Mesopotamian tablet problems to the high art of the Renaissance algebraists is discarded in favor of a disturbingly fractured, post-modern retelling with no characters, plot, or theme. The insistence that all numbers and expressions be put into various standard forms will provide additional confusion as to the meaning of identity and equality. Students must also memorize the quadratic formula for some reason.
为了不浪费宝贵的时间去思考数字及其规律,这门课转而专注于符号和符号操作规则。从古代美索不达米亚泥板上的问题,到文艺复兴时期代数学家的高超艺术,这条流畅的历史脉络被抛弃了,取而代之的是一段令人不安的、碎片化的后现代式叙述——没有角色、没有情节、没有主题。课程坚持要求所有数字和表达式都必须转化为各种“标准形式”,这进一步混淆了“恒等”和“相等”的含义。不知为何,学生还必须记住二次方程求根公式。
GEOMETRY
几何
Isolated from the rest of the curriculum, this course will raise the hopes of students who wish to engage in meaningful mathematical activity, and then dash them. Clumsy and distracting notation will be introduced, and no pains will be spared to make the simple seem complicated. This goal of this course is to eradicate any last remaining vestiges of natural mathematical intuition, in preparation for Algebra II.
这门课与课程体系的其他部分完全脱节。它会燃起那些希望进行有意义数学活动的学生的希望,然后又将其彻底击碎。课程会引入笨拙且干扰注意力的符号,不遗余力地把简单的东西变复杂。这门课的目标是根除学生最后一点自然的数学直觉,为代数 II 做准备。
ALGEBRA II
代数 II
The subject of this course is the unmotivated and inappropriate use of coordinate geometry. Conic sections are introduced in a coordinate framework so as to avoid the aesthetic simplicity of cones and their sections. Students will learn to rewrite quadratic forms in a variety of standard formats for no reason whatsoever. Exponential and logarithmic functions are also introduced in Algebra II, despite not being algebraic objects, simply because they have to be stuck in somewhere, apparently. The name of the course is chosen to reinforce the ladder mythology. Why Geometry occurs in between Algebra I and its sequel remains a mystery.
这门课的核心是无理由、不恰当地使用解析几何。圆锥曲线被放在坐标系中介绍,从而避开了圆锥及其截面本身的美学简洁性。学生要学习将二次形式改写成各种标准格式,却毫无理由可言。指数函数和对数函数也被塞进代数 II 中,尽管它们根本不是代数对象——显然只是因为总得找个地方放它们。课程名称被定为“代数 II”,是为了强化“阶梯神话”。而几何课为什么夹在代数 I 和代数 II 之间,至今仍是个谜。
TRIGONOMETRY
三角学
Two weeks of content are stretched to semester length by masturbatory definitional runarounds. Truly interesting and beautiful phenomena, such as the way the sides of a triangle depend on its angles, will be given the same emphasis as irrelevant abbreviations and obsolete notational conventions, in order to prevent students from forming any clear idea as to what the subject is about. Students will learn such mnemonic devices as “SohCahToa” and “All Students Take Calculus” in lieu of developing a natural intuitive feeling for orientation and symmetry. The measurement of triangles will be discussed without mention of the transcendental nature of the trigonometric functions, or the consequent linguistic and philosophical problems inherent in making such measurements. Calculator required, so as to further blur these issues.
两周就能讲完的内容,被无意义的定义绕来绕去拖成了一整个学期的课程。三角形的边长如何随角度变化等真正有趣、美丽的现象,会与无关的缩写和过时的符号惯例被同等强调,目的是不让学生对这门学科的本质形成清晰认知。学生要学习“SOHCAHTOA”(正弦=对边/斜边,余弦=邻边/斜边,正切=对边/邻边)、“All Students Take Calculus”(所有学生学微积分,用于记忆三角函数在各象限的符号)这类记忆口诀,而不是培养对方向和对称性的自然直觉。课程会讨论三角形的测量,却不提三角函数的超越性,也不提这种测量本身所蕴含的语言和哲学问题。课程要求使用计算器,进一步掩盖这些问题。
PRE-CALCULUS
预备微积分
A senseless bouillabaisse of disconnected topics. Mostly a half-baked attempt to introduce late nineteenth-century analytic methods into settings where they are neither necessary nor helpful. Technical definitions of ‘limits’ and ‘continuity’ are presented in order to obscure the intuitively clear notion of smooth change. As the name suggests, this course prepares the student for Calculus, where the final phase in the systematic obfuscation of any natural ideas related to shape and motion will be completed.
一堆毫无关联的主题乱炖而成的大杂烩。课程多半是半生不熟地试图将19世纪后期的分析方法,引入到既不必要也无帮助的场景中。课程会给出“极限”和“连续性”的技术定义,目的是掩盖“平滑变化”这个直观清晰的概念。正如其名称所示,这门课是为微积分“做准备”——在微积分课上,对形状和运动相关的自然思想进行系统性混淆的最后阶段,将彻底完成。
CALCULUS
微积分
This course will explore the mathematics of motion, and the best ways to bury it under a mountain of unnecessary formalism. Despite being an introduction to both the differential and integral calculus, the simple and profound ideas of Newton and Leibniz will be discarded in favor of the more sophisticated function-based approach developed as a response to various analytic crises which do not really apply in this setting, and which will of course not be mentioned. To be taken again in college, verbatim.
这门课会探讨运动的数学原理,以及如何用一大堆不必要的形式主义将其掩盖。尽管课程号称是微分和积分微积分的入门,但牛顿和莱布尼茨提出的简单而深刻的思想会被抛弃,取而代之的是更复杂的、基于函数的方法——这种方法是为应对各种分析学危机而发展出来的,但这些危机在入门阶段并不适用,课程当然也不会提及这些背景。这门课在大学里还会被原封不动地再学一遍。
And there you have it. A complete prescription for permanently disabling young minds— a proven cure for curiosity. What have they done to mathematics!
以上就是全部内容。这是一份让年轻人思维永久僵化的完整方案——一种经证实能扼杀好奇心的“疗法”。他们对数学做了什么啊!
There is such breathtaking depth and heartbreaking beauty in this ancient art form. How ironic that people dismiss mathematics as the antithesis of creativity. They are missing out on an art form older than any book, more profound than any poem, and more abstract than any abstract. And it is school that has done this! What a sad endless cycle of innocent teachers inflicting damage upon innocent students. We could all be having so much more fun.
这门古老的艺术形式,有着令人惊叹的深度和令人心碎的美丽。多么讽刺啊,人们竟然将数学视为创造力的对立面。他们错过了一种比任何书籍都古老、比任何诗歌都深刻、比任何抽象艺术都抽象的艺术形式。而这一切都是学校造成的!无辜的教师对无辜的学生造成伤害,形成了一个可悲的无尽循环。我们本可以享受更多乐趣的。
SIMPLICIO: Alright, I’m thoroughly depressed. What now?
辛普利西奥:好吧,我彻底沮丧了。现在该怎么办?
SALVIATI: Well, I think I have an idea about a pyramid inside a cube…
萨尔维亚蒂:嗯,我想我有个关于立方体里金字塔的想法……
Teaching Mathematics—Graph Theory
数学教学——图论
2011-06-26 2011 年 6 月 26 日
community service
社区服务
Mathematics is supposed to be a process of discovery. Definitions, propositions, and methods of proof don’t come from nowhere, although after the fact (when presented in a textbook) they often seem to. As opposed to a textbook, real maths is highly non-linear. It took mathematicians quite a lot of fuss to come up with the quadratic formula, and even simple geometric conjectures were for the longest time the subject of hot debate.
数学本应是一个发现的过程。定义、命题和证明方法并非凭空而来,尽管在事后(当它们出现在教科书中时)它们常常显得如此。与教科书不同,真正的数学是非线性的。数学家们费了很大的劲才推导出二次公式,甚至简单的几何猜想也曾长时间是激烈争论的主题。
I feel like if I’m going to be a teacher worth anyone’s time, I have to let students in on the secret that questions guide mathematics. This urge to teach is especially strong at the high school level, where it is generally agreed that “mathematics education” is a farce.
我觉得,如果我要成为一个值得他人花时间的老师,我必须让学生知道是问题引导着数学的发展。这种教学的冲动在高中阶段尤为强烈,因为人们普遍认为“数学教育”是个笑话。
And so, as the only community service I do regularly (and too seldom, at that), I go to local high schools and middle schools and give “lectures” on mathematics. Though I have ideas for a lot of lectures I could give, and wish I had more than just an hour to work with a class, I usually stick to a particularly intuitive lecture on graph theory. I will reproduce one such lecture here, picking out the best of the student’s innovation that I can remember. Regular text paraphrases what I speak and what is written on the board, quoted text is student response, and square brackets [ ] contain commentary.
因此,作为我唯一经常进行的社区服务(尽管次数太少),我会去当地的高中和初中进行数学“讲座”。尽管我有许多讲座的想法,并且希望有超过一个小时的时间与班级互动,但我通常坚持进行一场关于图论的特别直观的讲座。我将在这里重现这样一场讲座,挑选出我记忆中学生最具创新性的想法。普通文本是对我说的内容和写在黑板上的内容的释义,引号中的文本是学生的回应,方括号 [ ] 包含评论。
As a note to the reader, this will serve as a very detailed introduction to Graph Theory, as opposed to the terse primers I’ve been providing thus far.
作为对读者的说明,这将是对图论的非常详细的介绍,与我之前提供的简短入门不同。
Two Puzzles
两个谜题
Today we are going to do three things:
今天我们将做三件事:
- Think about some puzzles,
思考一些谜题, - Do some mathematics,
进行一些数学思考, - Use math to change the world.
利用数学改变世界。
So here are the two puzzles:
那么,这两个谜题是:
First, [after asking a student to provide her name, I invent a city name based on it] imagine you’re the mayor of Erintown. In Erintown there are seven very old and beautiful bridges, and as mayor you’d like to promote their prominence in tourism. To do this, you wish to provide a route through the city which crosses every bridge exactly once, never visiting the same bridge twice. The seven bridges are arranged as follows [a much more detailed picture than what one draws on a white board]:
首先,[在询问一位学生她的名字后,我根据这个名字虚构了一个城市的名字] 想象你是 Erintown 的市长。在 Erintown 有七座非常古老且美丽的桥,作为市长,你希望在旅游中突出这些桥的重要性。为此,你希望提供一条穿过城市的路线,这条路线恰好经过每座桥一次,且不会重复经过同一座桥。这七座桥的布局如下 [比在白板上画的更详细的图]:
Bridges of Erintown
Erintown 的桥
The informed reader will recognize this immediately as the Seven Bridges of Königsberg problem, which historically founded graph theory, and was solved by Leonard Euler in the 18th century. But honestly, what (potentially immature) high school student is interested in a problem with a name like that? As we will see throughout the post, personalization (and the engagement inherent in it) is essential to the success of the lecture.]
[熟悉这一问题的读者会立刻认出,这就是 哥尼斯堡七桥问题,它在历史上开创了图论,并且在 18 世纪被莱昂哈德·欧拉解决。但说实话,哪个(可能还不太成熟)高中生会对这样一个名字的问题感兴趣呢?正如我们在整个帖子中将看到的,个性化(以及其中固有的参与感)对于讲座的成功至关重要。]
Unfortunately, after a few tries you are unable to find a route which works. Hence the first puzzle is: does such a route exist? If not, how can we prove it?
不幸的是,在尝试了几次之后,你无法找到一条可行的路线。因此,第一个谜题是:这样的路线是否存在?如果不存在,我们如何证明它?
[At this point, we clarify some rules of the puzzle. High school students are adept at producing loopholes, and rightfully they enjoy doing so. So typically we talk about swimming, aircraft, traversing bridges halfway, teleportation, etc., banishing each possibility as it comes up. This is an important step, because in part the whole point of the mathematical formulation of this problem is to eliminate these possibilities from consideration. We very much need to rephrase this problem entirely in our minds to extract the aspects we care about and discard the rest. Even when in real life swimming is an option, our mathematical formulation must ignore swimming, and hence we must design it appropriately (and hopefully elegantly).]
[在这一点上,我们澄清了一些谜题的规则。高中生很擅长找出漏洞,而且他们理所当然地喜欢这样做。所以我们通常会讨论游泳、飞机、半途过桥、瞬间移动等,每出现一种可能性就将其排除。这是一个重要的步骤,因为这个问题的数学表述的一个主要目的就是排除这些可能性。我们确实需要在脑海中完全重新表述这个问题,以提取我们关心的方面并丢弃其余部分。即使在现实生活中游泳是一个选项,我们的数学表述也必须忽略游泳,因此我们必须适当地设计它(并且希望是优雅的)。]
For the second problem, say you’re at a party of one hundred people. At this party, someone decides to start tallying up who at the party is friends with whomelse (he’s one of those guys, a drama king). He shows his list to you, and you notice that there are two people at the party who have the same number of friends at the party. The thought occurs to you that this will always be the case, no matter how many people attend and who is friends with whom.
第二个问题,假设你参加了一个有一百人的派对。在这个派对上,有人决定开始统计派对上谁和谁是朋友(他就是那种喜欢制造戏剧性的人)。他把他的名单给你看,你注意到派对上有两个人在派对上的朋友数量相同。你突然想到,这种情况总会发生,不管有多少人参加派对以及谁和谁是朋友。
So the second puzzle is: at a party of
n
n
n people, must it be true that there exist two people with the same number of friends at the party?
所以第二个谜题是:在一个有
n
n
n 人的派对上,是否必然存在两个人在派对上的朋友数量相同?
[Again, we have the requisite loopholes, like whether there are stalkers at the party, and whether you are friends with yourself. The former drives us to distinguish that we want “symmetric” friendships, i.e. if you are friends with someone then they are friends with you. The former translates to undirected edges later, while the latter hints at simple graphs. Both are usually made clear by appealing to the rules of Facebook friendship. Finally, we might make the clarification that there are at least two people at the party, in order to prevent a discussion of vacuously true statements.]
[同样,我们有必要的漏洞,比如派对上是否有跟踪狂,以及你是否和自己是朋友。前者促使我们区分我们想要的是“对称”的友谊,即如果你和某人是朋友,那么他们也和你是朋友。前者后来转化为无向边,而后者暗示了简单图。通常通过引用 Facebook 友谊的规则来澄清这两点。最后,我们可能会澄清派对上至少有两个人,以防止讨论空洞的真命题。]
Now take five minutes and try to solve these problems, by yourself, with a friend, or with a group, however you feel most comfortable tackling a problem. [They never get very far, but at least once I’ve encountered a student who knew of the Seven Bridges problem ahead of time, spoiling much of the fun and thoroughly confusing the rest of the class.]
现在花五分钟,尝试自己解决这些问题,或者和朋友一起,或者和小组一起,以你觉得最舒服的方式来解决问题。[他们通常进展不大,但至少有一次我遇到了一个已经知道七桥问题的学生,这破坏了大部分乐趣,并且让其他同学感到非常困惑。]
New Mathematics
新的数学
[After five to ten minutes pass and the group is quiet again] So, who thinks they’ve solved the first problem? [hands raise, most proclaiming impossibility; those who try to explain their reasoning mostly resign to awkward case-checking or saying they just couldn’t find one that worked] And what about the second? [nobody raises a hand, most enjoy thinking about the bridges problem because it is very visual. In classrooms blessed with a SmartBoard, I can have a number of them come up to the front and attempt to draw a route with their finger (and hitting undo when they invariably fail, so that I don’t have to redraw the diagram every time).]
[五到十分钟过去,小组再次安静下来] 那么,谁认为他们解决了第一个问题?[有人举手,大多数宣称这是不可能的;那些试图解释他们推理的人大多只能进行尴尬的逐案检查,或者说是他们找不到一个可行的方案] 第二个问题呢?[没有人举手,大多数人都喜欢思考桥梁问题,因为它非常直观。在配备了 SmartBoard 的教室里,我可以让他们中的一些人来到前面,用手指尝试画出一条路线(当他们不可避免地失败时按下撤销,这样我就不用每次都重新画图了)。]
So, it appears that we haven’t come up with a good solution for either problem. Now a mathematician might say at this point, “screw this, I’m going to make up my own math to solve it!” And that’s what we’re going to try to do.
所以,看来我们还没有为这两个问题找到一个很好的解决方案。现在一个数学家可能会在这个时候说:“管它呢,我要自己发明数学来解决它!” 这就是我们要尝试去做的。
The first step is to compare the problems: what is similar and what is different? [Discussion ensues, but often times the students don’t understand what I’m looking for, and usually the problem is that they’re trying to come up with the “correct” answer instead of making observations; it is a curse of the schooling paradigm. Additional leading questions include:] what are the subjects of our study? How are they related? does it matter where you walk on a landmass between visiting bridges? Does it matter where the people in the party are standing? [And the most important question] Is there a better way to draw these problems?
第一步是对比这两个问题:它们的相似点和不同点是什么?[讨论开始了,但通常学生们并不理解我在寻找什么,通常的问题是他们试图找到“正确”的答案,而不是进行观察;这是学校教育体系的弊端。更多的引导性问题包括:] 我们研究的主题是什么?它们之间有什么关系?在访问桥梁之间在陆地上行走的位置重要吗?派对上人们站立的位置重要吗?[以及最重要的问题]有没有更好的方式来绘制这些问题?
[Soon enough students make the right observations, that our drawings of the two problems are almost identical!] It doesn’t actually matter how big or where the landmasses are, since all we care about is the order in which we cross bridges. Hence we can compress the landmasses down to dots! Additionally, we can just draw people as dots, and arrange them in any way we wish. Then, the bridges and friendships become lines connecting the dots. This yields a much nicer picture for the bridges problem, and a similar one for the party problem.
[很快学生们做出了正确的观察,我们绘制的这两个问题几乎一模一样!] 陆地的大小和位置其实并不重要,因为我们关心的是过桥的顺序。因此我们可以把陆地压缩成点!此外,我们也可以把人画成点,并且可以随意排列它们。然后,桥和友谊变成了连接这些点的线。这为桥的问题提供了一个更美观的图像,也为派对问题提供了一个类似的图像。
By writing the problem this way, we have distilled out the relevant facts: all we really care about is the structure of how these things are connected**.** Unfortunately we have one problem: we don’t have names for these things! We certainly don’t want to call them bridges and landmasses, or people and friendships, because we want the picture to apply to both problems at the same time.
通过这种方式表述问题,我们提炼出了相关的事实:我们真正关心的是这些东西连接的结构**。** 不幸的是我们有一个问题:我们没有这些东西的名字!我们当然不想把它们叫做桥和陆地,或者人和友谊,因为我们希望这个图像能同时适用于这两个问题。
So to start, what would we call the picture as a whole? Appeal to your imagination about what it looks like. [Though this part is sometimes difficult, especially at the middle-school level, eventually someone calls out something truly clever] “How about a constellation?”
那么首先,我们把这幅图整体叫什么呢?发挥你的想象力,想想它看起来像什么。[虽然这一部分有时比较困难,特别是在中学阶段,但最终总有人会喊出一个真正聪明的名字] “叫星座怎么样?”
I like that! So here we are, this is our invention:
我喜欢这个名字!所以,我们现在有了我们的发明:
Constellation Theory
星座理论
What are we going to call the individual dots? “Stars!” And what about the lines connecting them? “How about…connections?” Okay. So here is our first definition:
我们把单个的点叫什么呢?“星星!”那么连接它们的线呢?“叫……连接怎么样?”好的。那么这是我们的第一个定义:
Definition: A constellation has three parts:
定义: 一个星座有三个部分:
-
A set of stars S S S [we just accept the intuitive definition of a set without issue],
一组星星 S S S [我们直接接受集合的直观定义,没有问题], -
A set of connections C C C,
一组连接 C C C, -
A function f : C → S × S f: C \to S \times S f:C→S×S which accepts a connection and tells us which two stars it is connected to.
一个函数 f : C → S × S f: C \to S \times S f:C→S×S,它接受一个连接并告诉我们它连接的是哪两颗星星。
[Before the third, I ask the class whether the first two alone are enough. If I get nods, I draw a random collection of dots and lines, with the lines not at all connected to the dots, and they see we need some statement of incidence.]
[在第三部分之前,我问班级前两个部分是否足够。如果我得到点头,我就画一组随机的点和线,这些线根本就没有连接到点上,于是他们就会明白我们需要某种关联性的表述。]
Don’t be afraid of the third part (even if you don’t know what a function is), it’s just a formality that uses other (well-established) maths to make our definition consistent. Math can sometimes be a notational nightmare, but all this means is that we can take any connection and easily say which two stars it connects. Since we will always draw constellations as a picture, we can just use the picture as our “function.”
不要害怕第三部分(即使你不知道什么是函数),它只是一个形式,使用其他(已经建立的)数学知识来使我们的定义保持一致。数学有时会是一个符号的噩梦,但这只是意味着我们可以随意取一个连接,并且很容易地说出它连接的是哪两颗星星。既然我们总是把星座画成一幅图,我们就可以直接把这幅图当作我们的“函数”。
Now can someone remind me again what we were looking for in the bridges problem? Right, a route through the city that hits every bridge exactly once. First we need to translate a “route” into our language of constellations. Does anyone have a good name? [After a few generic suggestions like “trail,” “path,” and “route,” we settle on the imaginative “waltz”.] This gives our second definition:
现在谁能再提醒我一下我们在桥的问题中寻找的是什么?对了,一条恰好经过每座桥一次的城市路线。首先我们需要把“路线”翻译成星座的语言。谁有个好名字?[在得到一些诸如“小径”“路径”和“路线”之类的普通建议后,我们最终选择了富有想象力的“华尔兹”。] 这就是我们的第二个定义:
Definition: A waltz through a constellation
(
S
,
C
,
f
)
(S,C,f)
(S,C,f) is a list of alternating stars and connections, which we label
(
s
1
,
c
1
,
s
2
,
c
2
,
…
,
s
n
−
1
,
c
n
−
1
,
s
n
)
(s_1, c_1, s_2, c_2, \dots, s_{n-1}, c_{n-1}, s_n)
(s1,c1,s2,c2,…,sn−1,cn−1,sn), where the
i
i
ith connection
c
i
c_i
ci is connected to its neighboring stars in the list
s
i
,
s
i
+
1
s_i, s_{i+1}
si,si+1. In terms of our function,
f
(
c
i
)
=
(
s
i
,
s
i
+
1
)
f(c_i) = (s_i,s_{i+1})
f(ci)=(si,si+1) for each
i
=
1
…
n
−
1
i=1 \dots n-1
i=1…n−1.
定义: 一个通过星座
(
S
,
C
,
f
)
(S,C,f)
(S,C,f) 的华尔兹是一个交替的星星和连接的列表,我们将其标记为
(
s
1
,
c
1
,
s
2
,
c
2
,
…
,
s
n
−
1
,
c
n
−
1
,
s
n
)
(s_1, c_1, s_2, c_2, \dots, s_{n-1}, c_{n-1}, s_n)
(s1,c1,s2,c2,…,sn−1,cn−1,sn),其中第
i
i
i 个连接
c
i
c_i
ci 与其列表中的相邻星星
s
i
,
s
i
+
1
s_i, s_{i+1}
si,si+1 相连。用我们的函数来表示,
f
(
c
i
)
=
(
s
i
,
s
i
+
1
)
f(c_i) = (s_i,s_{i+1})
f(ci)=(si,si+1) 对于每个
i
=
1
…
n
−
1
i=1 \dots n-1
i=1…n−1 都成立。
This is just a way to write out on paper what the waltz is. [I label the seven bridges picture and provide an example.] You who suggested the name “waltz,” what is your name? “Phil.” What is your last name, Phil? “Osman.” Great! Now we have another definition:
这只是把华尔兹写在纸上的一个方法。[我标记了七桥的图像并提供了一个例子。] 你提出了“华尔兹”这个名字,你叫什么名字?“菲尔。”菲尔,你的姓是什么?“奥斯曼。”太好了!现在我们有了另一个定义:
Definition: An Osmannian waltz through a constellation is a waltz which uses each connection in
C
C
C exactly once.
定义: 一个通过星座的奥斯曼华尔兹是一个恰好使用
C
C
C 中每个连接一次的华尔兹。
[A few giggles resound when they realize I’m incorporating the student’s name into the definition.] Now can somebody rephrase the original problem in terms of constellation theory? “We want to find out if there is an Osmannian waltz in that particular constellation.” Excellent!
[当他们意识到我把学生的姓名纳入定义时,引起了一些笑声。] 现在谁能用星座理论重新表述原来的问题?“我们想知道那个特定的星座中是否存在一个奥斯曼华尔兹。”太好了!
Now let’s turn our attention to the party problem. Can someone remind me what we were trying to find out about parties? “Whether there are two people who have the same number of friends.” Right, whether that has to be the case for any party. Now in terms of constellations, what is that? “The number of connections at each star.” Great. What’s your name? “Olivia.” Olivia, what’s your last name? “Bisel.” Okay. Here’s another definition:
现在让我们把注意力转向派对问题。谁能提醒我一下我们试图了解派对的什么情况?“是否有两个人拥有相同数量的朋友。”对,在任何派对上是否必然如此。那么用星座来说,那是什么?“每颗星的连接数量。”太好了。你叫什么名字?“奥利维亚。”奥利维亚,你的姓是什么?“比塞尔。”好的。这是另一个定义:
Definition: The Bisel-degree of a star is the number of connections in
C
C
C connected to it.
定义: 一颗星的比塞尔度数是
C
C
C 中与它相连的连接数量。
Now there are a couple of other details we have to consider. Specifically, in a general constellation we never ruled out multiple connections connecting the same two stars. And we never said a connection can’t go from a star to itself. But we must rule these out to make a sensible party problem. So we will call a constellation which rules out doubled connections and self-connections simple. [For the sake of time, we just provide a name, and it’s not that imaginative of a property anyway.]
现在我们还得考虑一些其他细节。具体来说,在一个一般的星座中,我们从未排除连接同一对星星的多个连接。我们也从未说过一个连接不能从一颗星连向它自己。但我们必须排除这些情况,才能使派对问题有意义。因此,我们将排除了重复连接和自连接的星座称为简单的。[为了节省时间,我们只是提供了一个名称,而且这也不是一个很有想象力的属性。]
So can someone translate the party problem into the language of simple constellations? “It’s whether every simple constellation has to have two stars with equal Bisel-degree.” Wonderful!
那么谁能用简单星座的语言来表述派对问题?“就是每一个简单星座是否必然有两颗星的比塞尔度数相等。”太棒了!
Now that we have a working language, let’s take another ten minutes to try to solve the problems. But this time, you aren’t allowed to use “bridges,” “landmasses,” “people,” or “friendships” anymore, you have to use the terms we invented. [The students still don’t get far, especially on the bridges problem, but every now and then a student solves the party problem. As they work, I give subtle hints, like, “what happens if you add extra connections or remove some? Does it work then? What aspect of the intrinsic structure have you altered by doing this? Try lots of examples!”]
现在我们有了一个可以工作的语言,让我们再花十分钟来尝试解决这些问题。但这次,你们不被允许再使用“桥”“陆地”“人”或者“友谊”,你们必须使用我们发明的术语。[学生们仍然没有取得很大进展,特别是在桥的问题上,但每隔一段时间就会有学生解决派对问题。在他们工作时,我会给出一些微妙的提示,比如,“如果你增加一些额外的连接或者去掉一些,会发生什么?那样行得通吗?通过这样做,你改变了内在结构的哪个方面?多试一些例子!”]
[After bringing the class back together] So who thinks they’ve solved the first problem? [a few hands raise] “I think it has something to do with whether the Bisel-degree is even or odd.” Interesting. Did you get much further than that? “No…” Okay. What about the party problem? “I think I have it. So if everybody had a different number of friends, then one person would have to have no friends and someone would have to be everyone’s friend, but that can’t happen.”
[把班级重新召集起来后] 那么谁认为他们解决了第一个问题?[有几只手举了起来] “我觉得这和比塞尔度数是偶数还是奇数有关。”有意思。你有没有进一步的发现?“没有……”好吧。那派对问题呢?“我觉得我明白了。如果每个人都有不同数量的朋友,那么就会有一个人没有朋友,而有一个人是每个人的朋友,但这是不可能的。”
Did everyone hear that? [I reiterate on the board in detail, explaining the idea behind proof by contradiction, and drawing a picture of the resulting constellation.] This is a very elegant proof. And if anyone can come up with a solid proof of the bridge problem, I have no doubt your teacher would give ample extra credit.
大家都听到了吗?[我在黑板上详细地重述了一遍,解释了反证法的思想,并画出了结果星座的图像。]这是一个非常优雅的证明。如果有人能对桥的问题提出一个可靠的证明,我毫不怀疑你的老师会给大量的额外学分。
Changing the World
改变世界
Now, for the mathematician this is enough. This new mathematical object, a constellation, is full of wonderful patterns that we could spend our entire lives thinking about (and many have done just this). However, it’s probably true that most of you aren’t going to become mathematicians. So let’s try to think of things in the real world that we can model as constellations. Any ideas?
现在,对于数学家来说这就足够了。这个新的数学对象,星座,充满了美妙的模式,我们可以用一生的时间去思考(许多人确实这样做了)。然而,很可能你们大多数人并不会成为数学家。所以让我们试着去想一想现实世界中可以用星座来建模的事物。有什么想法吗?
The students suggest a variety of different (and usually complex) ideas, including trade between nation-states, distributions of power among people, and the structure of galaxies. For each example, I usually have to verbally augment our representation of a graph (for the sake of time), bringing constellations with numerically labeled edges or directed connections. Since I always tell the students to “think bigger,” they inevitably say “galaxies,” and I have to explain why that doesn’t work, because the whole point of constellations (the mathematical ones) is that the relative sizes and positions of the stars don’t matter, whereas at the galactic level that completely determines the connection (which is invariably gravitational pull). We apologize for the terminological confusion.
学生们提出了各种不同的(通常是复杂的)想法,包括国家之间的贸易、人与人之间的权力分配以及星系的结构。对于每一个例子,我通常都必须口头补充我们对图的表示(为了节省时间),引入带有数字标记的边或有向连接的星座。因为我总是告诉学生们“想得更大一些”,所以他们不可避免地说出了“星系”,而我不得不解释为什么这行不通,因为星座(数学意义上的)的全部要点是星星的相对大小和位置并不重要,而在星系层面上,这些完全决定了连接(这通常是引力)。我们为术语上的混淆道歉。
Eventually, we might get to the cases of modelling all roads and intersections, after which I claim that is exactly how Google Maps (and all other mapping/directions software) works. Sometimes they take the “friendship” hint and recognize Facebook as a constellation, and we often begin to talk about friend suggestions and degrees of separation. Finally, (and this is the main example I wish to work toward), we model the entire internet as a constellation, with directed connections corresponding to links between web sites. Then I talk about how Google based their company on the soundness of this particular model, making 25 billion dollars and changing the world. We do not discuss software representations of constellations, nor algorithms to extract data from them (this would be a whole course worth of information, at least).
最终,我们可能会谈到对所有道路和交叉路口的建模,之后我声称这正是谷歌地图(以及所有其他地图/导航软件)的工作原理。有时他们会从“友谊”的提示中意识到 Facebook 是一个星座,然后我们经常开始谈论朋友推荐以及六度分隔。最后,(这是我最想讨论的主要例子),我们将整个互联网建模为一个星座,其中的有向连接对应于网站之间的链接。然后我谈到谷歌是如何基于这个特定模型的可靠性建立他们的公司的,赚了 250 亿美元并改变了世界。我们没有讨论星座的软件表示,也没有讨论从它们中提取数据的算法(这至少是一门完整的课程的信息)。
Depending on the amount of remaining time, I either provide the proof of the party problem, if the students didn’t solve it on their own, or continue with anecdotes about Google’s PageRank and its pitfalls. I don’t usually give the proof of the seven bridges problem, but if pressed a short sketch of the proof is easy. More often than not, the bell ends my lecture before I’m ready anyway.]
[根据剩余时间的多少,我会提供派对问题的证明(如果学生们自己没有解决的话),或者继续讲述谷歌的 PageRank 及其陷阱的轶事。我通常不提供七桥问题的证明,但如果被要求,一个简短的证明草图是很容易的。很多时候,铃声在我还没准备好之前就结束了我的讲座。
I should emphasize that the proof of the party problem is the most exciting moment of the entire lecture. There is often a few students that have an audible “whoa!” and I’ve even received a standing ovation. This tells me that basic elegant proofs are easily within reach of a freshman high school student, and even the obviously “popular” girls have admitted to me it’s cool.
[我应该强调,派对问题的证明是整个讲座中最激动人心的时刻。常常会有一些学生发出惊叹的“哇哦!”,我甚至收到过起立鼓掌。这让我明白,对于一个高中新生来说,简单的优雅证明是很容易理解的,甚至连那些显然很“受欢迎”的女生也承认这是很酷的。
Reflections
反思
This lecture has generally been successful among students for three obvious reasons.
这个讲座通常在学生中很成功,原因有三个。
First, it is exploratory. People intrinsically like puzzles. In sharp contrast to the typical high-school style of memorization and repetition, the students drive the method! Of course, they do so in a discordant, chaotic way, but this can just as easily be said of the same students English essays or history papers. They simply have less practice with this particular kind of argument, and so they are expectantly less coherent.
首先,它是探索性的。人们天生就喜欢谜题。这与典型的高中死记硬背和重复的学习方式形成了鲜明的对比,学生们推动了这种方法!当然,他们的方法是不和谐的、混乱的,但这同样也可以说在他们的英语作文或历史论文中。他们只是对这种特定的论证方式缺乏练习,因此他们的表达也就不那么连贯。
Unfortunately the shortage of time forces me to guide them much more directly than I should. The amount of content we cover in an hour lecture really deserves a week of discussion, formulation and reformulation, and debate, with as little intervention as possible. I would absolutely love a chance to work with them for an extended period of time to see how it plays out. And of course, it would be much less linear, and we’d explore the questions of the students interest. However, I do fear that they might prefer a more rigid structure, being used to the humdrum of their education heretofore.
不幸的是,时间的不足迫使我比应该的更直接地引导他们。我们在一小时的讲座中所涵盖的内容实际上值得用一周的时间来进行讨论、制定和重新制定,以及辩论,尽可能少地进行干预。我真的很希望能有机会和他们一起长时间地工作,看看结果会如何。当然,这将更加非线性,我们会探索学生们感兴趣的问题。然而,我确实担心他们可能更喜欢一个更严格的结构,因为他们已经习惯了他们目前教育的单调性。
Second, the lecture is personal. I don’t have them make up names for nothing. Mathematics is a generative subject. The students not only need to see that, but also experience the process of taking an intuitive idea and nailing it down (often with more logical rigor than anything they’ve experienced in math to date). Inventing a name for the resulting definition secures the idea in their memory, and accentuates the notion that this thing is unique to their special classroom community. Since they don’t yet have the practice or motivation to make their own proofs (the ultimate mathematical self-expression), this is the next best thing. But most of all, naming the concepts is fun!
第二,这个讲座是个性化的。我不是毫无理由地让他们起名字。数学是一门创造性的学科。学生们不仅需要看到这一点,还需要经历将一个直观的想法确定下来的过程(通常比他们到目前为止在数学中经历的任何事情都需要更多的逻辑严谨性)。为最终的定义发明一个名字可以将这个想法固定在他们的记忆中,并强调这个概念是他们独特的课堂社区所独有的。由于他们还没有自己证明的实践或动力(这是最终的数学自我表达),这是次优的选择。但最重要的是,给概念起名字是有趣的!
So I frame the problems in their imaginations, not history. I give them no false pretense for why we are doing this. The puzzle is a means to its own end, and we only later discover that our work is applicable. For a large portion of mathematical history, one might argue, this is how progress worked. Certainly Leonhard Euler anticipated neither Facebook’s social graph nor Google Maps in the mid 18th century. This is the easiest way to impress upon them that many different things have similar patterns in their structure, so even studying a trivial thing can be very enlightening. The puzzles really are worth doing for their own sake.
所以我把这些问题放在他们的想象中,而不是历史中。我没有为我们的行为找任何虚假的理由。这个谜题本身就是它的目的,我们只是后来才发现我们的工作是有用的。在数学历史的大部分时间里,人们可能会说,这就是进步的方式。当然,莱昂哈德·欧拉在 18 世纪中期既没有预料到 Facebook 的社交图谱,也没有想到谷歌地图。这是最容易让他们明白,许多不同的事物在结构上有相似的模式,所以即使是研究一个微不足道的东西也可以非常有启发性。这些谜题确实值得为了它们自己而去做。
Compare this to being given the definitions and propositions in the established mathematical language. To an untrained, uninterested student, this is not only confusing, but boring beyond belief! They don’t have the prerequisite intuition for why the definition is needed, and so they are left mindlessly following along at best, and dozing off at worst.
把这和被给予已建立的数学语言中的定义和命题相比。对于一个未经训练、不感兴趣的学生来说,这不仅令人困惑,而且极其无聊!他们没有对为什么需要这个定义的直觉,所以他们最多只能毫无目的地跟着走,最坏的情况是打瞌睡。
Third, the lecture is a conversation. While ultimately I have to dish out judgement on their suggestions (this name doesn’t make sense, that idea doesn’t pan out for this reason, etc.), I make an honest effort to explain why and reiterate our goals, showing the discrepancy, and then requesting another suggestion. Unfortunately that keeps it as a bona-fide lecture, but if I had a week, the students would ideally critique each other’s work.
第三,这个讲座是一场对话。尽管最终我必须对他们提出的建议做出评判(这个名字没有意义,那个想法因为这个原因没有成功,等等),我真诚地努力解释原因,重述我们的目标,指出差异,然后请求另一个建议。不幸的是,这仍然是一场真正的讲座,但如果我有一周的时间,学生们将理想地互相批评对方的工作。
At the same time, I do (to some bounded level) entertain their admittedly immature suggestions. When they keep insisting swimming or long jumping across the river, I usually quip with something like, “Pretend the tourist is your grandmother. Would she swim that far?” If not to just deny their question, this reminds them that the original puzzle was meant for all tourists, including the “weakest link” as far as swimming goes. Even when they riposte with “Yes. My grandmother is a body-builder,” I dismiss it with a smirk and a wave of the hand, perhaps sarcastically saying, “Okay.” I feel that such a level of humorous improvisation is necessary, both to keep the students on their toes and to mirror their creativity with my own, thus fueling it and directing it toward the mathematics.
同时,我也(在一定程度上)接受他们承认是幼稚的建议。当他们坚持要游泳或远跳过河时,我通常会用类似这样的话来回应:“假设游客是你的祖母。她会游那么远吗?”如果不仅仅是为了拒绝他们的问题,这也提醒他们,原来的谜题是为所有游客设计的,包括在游泳方面最弱的一环。即使他们反驳说:“是的。我的祖母是健身运动员。”我也会带着微笑和挥手轻描淡写地回应,也许会讽刺地说:“好吧。”我觉得这种幽默的即兴发挥是必要的,既可以保持学生的警觉性,也可以用我自己的创造力来反映他们的创造力,从而激发它并引导它走向数学。
Of course, I might not always spend so much time with such verbal fencing. But for a first exposure to real mathematics, and to establish my role in part as an equal but more so as an obstacle, I deem it necessary. I need to be the out-witter, so that when they exhaust their loopholes, they have no choice but to beat me by solving the problem. Given a lengthier period of time (taking into consideration the students’ maturity level), I would gradually transition to a more pointed focus on the problems, and make it clear when silliness is appropriate. With luck and planning, interest in the problems would compensate for a perhaps dull state of order.
当然,我并不总是会花这么多时间在这样的口头争论上。但对于第一次接触真正的数学,以及确立我在某种程度上是平等的,但更多的是作为一个障碍的角色,我认为这是必要的。我需要成为一个智胜者,这样当他们用尽了所有的漏洞时,他们别无选择,只能通过解决问题来战胜我。考虑到学生的成熟度,如果有一段更长的时间,我会逐渐转向更明确地关注问题,并明确指出什么时候可以开玩笑。凭借运气和计划,对问题的兴趣将弥补可能的单调的秩序。
If I Had a Class
如果我有一个班级
Sometimes I entertain the thought that I might end up teaching high school, and that with the providence of the school’s administration I could have my own elective course called “Real Math,” or something perhaps more enticing to the skeptical student (“Math Soup for the Teenage Soul”? “Math as Art”? “Mathematical Composition”?).
有时我会想,我可能会去教高中,而且如果学校的管理层允许的话,我可以开设一门名为“真正的数学”的选修课,或者一些可能更吸引怀疑的学生的课程(“青少年心灵的数学汤”?“数学即艺术”?“数学创作”?)。
This course would start with a week of lectures similar to the one detailed above, and then alternate each week between some objective curricula (likely the basics of set theory and methods of proof) and an exploratory topic. The latter might likely start off as more explorations into graph theory (I’d debate whether to replace their invented names with the established language) and then continue into other basic topics. During the exploratory week, students would present and critique arguments in front of the class. The problems come from a list of problems given at the beginning of the week or the students’ own minds. And though I’d prefer most of the problems being the students’ own, it’s likely that initially most of the problems would come from me. Partial solutions, interesting observations, and even the process of an incorrect solution would all be presentation-worthy.
这门课程将以类似于上述详细的讲座开始,然后每周交替进行一些客观的课程(很可能是集合论的基础和证明方法)和一个探索性的话题。后者很可能一开始是图论的进一步探索(我会考虑是否用已建立的语言替换他们发明的名字),然后继续进入其他基础话题。在探索性的一周里,学生们将在全班面前展示并批评观点。这些问题来自一周开始时给出的问题列表或学生自己的想法。尽管我更希望大多数问题来自学生自己,但最初大多数问题可能还是来自我。部分解决方案、有趣的观察,甚至是错误解决方案的过程都值得展示。
And finally, perhaps the only original idea I would have for this course, the students would each keep a journal. It would double as a notebook for their own investigation of the material brought up during exploratory weeks and a portfolio to turn in for grading. Its grading would be largely subjective, but the students would have to display some level of effort in terms of the depth to which they explore a particular problem and the number of problems attempted. As the year would progress, I would get to know the students’ ability levels and work tendencies much more clearly, and would thus have a more refined and personalized grading method.
最后,也许这是我为这门课程唯一有的一个原创想法,每个学生都会保存一本日记。它既是他们在探索性的一周中对材料进行自我探究的笔记本,也是提交以供评分的作品集。它的评分将主要是主观的,但学生们必须在他们探索特定问题的深度以及尝试解决问题的数量方面表现出一定的努力。随着学年的进行,我会更清楚地了解学生的能力水平和工作习惯,因此会有一个更精细和个性化的评分方法。
Of course, not long after building up these ideas in my imagination, I came across the essay A Mathematician’s Lament, in which Paul Lockhart mercilessly (and rightfully) berates the current state of mathematics education in America. He more or less advocates the kind of teaching style I propose, and then argues that today’s mathematics teachers cannot play such a role for a lack of their own love for mathematics, and would not want to, because teaching this way is extremely hard! It requires much more work than the average teacher is paid to do, and there is no time for it when you’re berated by scripted curricula and standards and have six classes a day.
当然,在我的想象中构建了这些想法不久后,我看到了保罗·洛克哈特的论文一个数学家的哀叹,他无情地(而且正确地)批评了美国当前的数学教育现状。他或多或少地提倡我所提出的这种教学风格,然后论证说,今天的数学老师无法扮演这样的角色,因为他们自身缺乏对数学的热爱,而且他们也不想,因为用这种方式教学极其困难!这需要比普通教师得到的报酬更多的工作,而且当你受到固定的课程和标准的指责,并且一天有六节课时,根本没有时间来做这些。
After repeating the lecture above for five classes of students in the course of a single day, I certainly agree with Lockhart on the difficulty of this teaching method. Though I feel I have a natural knack for presentation and engagement, to handle the standard number of students per day expected of American teachers is quite tiring (and I am a lively and strapping young lad!). It’s clear that if mathematics education is going to be fixed, one big part will be in taking teachers out of the classroom for preparation, training, and reflection. That being said, I consider it my duty to take every opportunity to do a lecture, while it provides me both with intellectual joy and the satisfaction of beneficence.
在一天内为五个班级的学生重复了上述讲座后,我当然同意洛克哈特对这种教学方法的困难的看法。尽管我觉得我天生就擅长演讲和参与,但应对美国教师每天的标准学生数量相当令人疲惫(而我是一个活泼强壮的年轻人!)。很明显,如果数学教育要得到改善,一个重要的部分将是让教师离开教室进行准备、培训和反思。话虽如此,我认为抓住每一个机会进行讲座是我的责任,因为它既给我带来了智力上的快乐,也让我感到行善的满足。
discuss
LN
April 22, 2013 at 12:19 am Reply
感谢你理解一名高中数学学生不可避免的困惑。我非常希望能上你的课。
I just happened to stumble upon your blog, and although I do not quite grasp the concepts behind your posts, I find them very stimulating and their beauty truly mesmerizing (especially the simulation for cellular automata — is it somehow related to the Abelian sandpile?).
我偶然发现了你的博客,虽然我不太理解文章背后的概念,但我觉得这些内容极具启发性,其美感也令人着迷(尤其是元胞自动机的模拟——它是否与阿贝尔沙堆模型有某种关联?)。
I love math and programming. I mostly do independent studying aside from school, but sometimes it is difficult and discouraging; I wish I had a coach who I can turn to for help at times. May I ask for an advice for a future student pursuing the mathematics & computer programming field?
我热爱数学和编程。除了学校课程外,我主要靠自学,但有时会遇到困难,让人感到沮丧;我希望能有一位可以随时求助的指导者。请问你能给未来想从事数学与计算机编程领域的学生一些建议吗?
Also, are topics in graph theory accessible to a high school student? What kind of background is needed? I am looking for a topic for math research, but I am afraid that I do not have enough background. I’ve always been yearning to dive more into abstract math, and I hope to learn from the research experience.
另外,图论的相关主题对高中生来说容易理解吗?需要具备哪些基础?我正在寻找一个数学研究课题,但担心自己的基础不够。我一直渴望深入学习抽象数学,并希望从研究经历中有所收获。
- j2kun
April 22, 2013 at 12:27 am Reply
You should look into local organizations near you that foster mathematics learning for youths. For example, there is a thing called “Math Circle” in the midwest. I know there’s an analogous thing on the west coast, but I forget the name.
你可以了解一下你所在地区促进青少年数学学习的本地组织。例如,美国中西部有一个叫“数学圈”(Math Circle)的活动。我知道西海岸也有类似的活动,但想不起名字了。
Graph theory is definitely a great place to start. The only background you need is to learn how to do basic proofs (and I have a few posts in my Primers section on that to get you started). Knowing a little bit about set theory helps too, but I don’t think it’s entirely required.
图论绝对是一个很好的起点。你只需要掌握基本的证明方法(我的“入门指南”板块中有几篇相关文章,可以帮助你入门)。了解一点集合论也会有帮助,但我认为这并非必需。
I know there are a number of online courses (through Coursera, for example) that are “intro to proofs” type classes. These could be good resources, but they might go on the dry side of lecture-style math.
我知道有很多在线课程(例如通过 Coursera 平台)是“证明入门”类课程。这些可能是很好的资源,但它们的授课方式可能比较枯燥,偏向传统讲座式数学教学。
Chuck
May 4, 2013 at 10:31 pm Reply
This sort of exploratory activity is definitely where education is heading with the Common Core standards, but I would caution you against thinking that the only issue in teaching math lies in making curious activities like these. For one, the formalism you’ve presented here would require several weeks to carefully tread for high school students who have little experience with abstraction. The class you have described sounds great–full of students who are more interested in pondering interesting problems than gossiping or talking about the Clippers game. The fact is that many good teachers come up with fantastic and perplexing explorations with their students, but these lessons are only effective if students believe in themselves and have an intrinsic motivation to take ownership of their education. Some teachers do the hard work of engaging students in exploration, as you have, while also making and grading well-crafted assessments. That is hard work, as you’ve pointed out. However, that’s not the hardest part. The hardest is getting students who have given up and labeled themselves as failures to take interest and persevere in these interesting problems.
这种探索性活动无疑是美国共同核心标准(Common Core standards)下教育的发展方向,但我想提醒你,不要认为数学教学的唯一问题就在于设计此类有趣的活动。首先,对于几乎没有抽象思维经验的高中生来说,你所呈现的形式化内容需要数周时间才能逐步理解。你描述的班级听起来很棒——学生们更愿意思考有趣的问题,而不是闲聊或谈论快船队的比赛。事实上,许多优秀的教师都会与学生一起设计出色且令人困惑的探索活动,但这些课程只有在学生相信自己、并有内在动力主动掌控自己的学习时才会有效。有些教师像你一样,不仅努力让学生参与探索活动,还会设计并批改精心编写的作业和测试。正如你所指出的,这是一项艰巨的工作。然而,这还不是最困难的部分。最困难的是让那些已经放弃、并给自己贴上“失败者”标签的学生产生兴趣,并坚持完成这些有趣的问题。
- j2kun
May 4, 2013 at 10:45 pm Reply
I agree wholeheadtedly. I think the main necessity is a focus on equity for all students. I’ve even struggled with just what you’ve said in guest lectures I’ve given at schools in Chicago (comparable to, but not quite the south-side public schools). Assuming equity and self-motivation in general, most aversion to mathematics seems to be largely cultural. I hear the Finnish have a wonderful model, although how applicable it is to the American education system is debatable. At the very least, I think we should be paying our teachers more and requiring more from them.
我完全同意。我认为最关键的是要关注所有学生的公平教育机会。我在芝加哥的一些学校(与南区的公立学校类似,但不完全相同)做客座讲座时,就曾遇到过你所说的这种情况。如果暂且不考虑公平性和自我激励等普遍问题,大多数人对数学的反感似乎主要源于文化因素。我听说芬兰有一个非常好的教育模式,尽管它在美国教育体系中的适用性仍有待商榷。至少,我认为我们应该给教师更高的薪酬,并对他们提出更高的要求。
That being said, when I wrote this article the strongest image in my head were my colleagues from undergraduate mathematics who absolutely hated math but for some reason were dead set on teaching middle-school and high-school mathematics.
话虽如此,当我写这篇文章时,脑海中最清晰的画面是我本科时期的一些同学——他们极度讨厌数学,却不知为何执意要教初中和高中数学。
William Rutiser
May 12, 2013 at 9:28 pm Reply
Paul Lockhart’s book “Measurement” was published last summer. The book’s methods and goals are similar to yours. Most of my feelings are covered in the description and comments at amazon.com. Read the book slowly, don’t skip the problems, enjoy the process.
保罗·洛克哈特(Paul Lockhart)的著作《测量》(Measurement)于去年夏天出版。这本书的教学方法和目标与你的理念相似。我的大部分感受都在亚马逊网站的书籍描述和评论中有所体现。建议你慢慢阅读这本书,不要跳过习题,享受这个过程。
Nick
November 26, 2013 at 8:39 pm Reply
Hi Jeremy,
嗨,杰里米(Jeremy),
Just wanted to let you know I stumbled across your blog while I was searching for help with my topology homework and started getting carried away reading some of your posts. They’re all really good, but this one in particular was great. I am a first year grad student currently teaching a couple classes of freshman engineering calculus. This post made me think about what I’ve been doing both wrong and right this semester. (Mostly wrong) I was wondering what kind of experience you’ve had yourself as a TA and have you been able to incorporate any exploratory lessons like this one into the semester?
只想告诉你,我在查找拓扑学作业的帮助时偶然发现了你的博客,然后就一发不可收拾地读了你的一些文章。这些文章都非常棒,尤其是这一篇。我是一名一年级研究生,目前正在教两门大一工程微积分课程。这篇文章让我反思了这个学期我所做的事情中哪些是对的,哪些是错的(大部分是错的)。我想知道你自己作为助教有过哪些经历,以及你是否能够在这个学期中融入类似这样的探索性课程?
- j2kun
November 26, 2013 at 9:34 pm Reply
Calculus is in some sense the worst of the lot: students are only held accountable for computations, and the big ideas are (even in professors’ lectures) ignored entirely. College classes also have a particularly hard problem to overcome: the time budget. The best I’ve been able to manage is to deviate when relevant topics come up. For example, when students are arbitrarily forced to learn formulas for sums of numbers, squares, etc, I show them some of the beautiful proofs I have accumulated over the years. Other than that, all I can do is be direct and distinctly separate what’s truly important from what’s bogus textbook-filler crap or solely practice for the test. These overlap occasionally, of course, but not as often as I’d want.
从某种意义上说,微积分是所有数学课程中最糟糕的一门:学生只需要对计算负责,而那些核心思想(即使在教授的讲座中)也被完全忽略了。大学课程还有一个特别难克服的问题:时间预算。我所能做的最好的事情,就是在相关主题出现时适当偏离教学大纲。例如,当学生被强行要求学习数列求和、平方和等公式时,我会向他们展示我多年来积累的一些优美的证明方法。除此之外,我只能直截了当地将真正重要的内容与那些虚假的教材填充内容或仅为考试而设的练习区分开来。当然,这两者偶尔会有重叠,但重叠的频率远低于我的期望。
Even after three years of being a TA, I still get exasperated with my inability to avoid sending the loud message: math is extremely boring and mechanical. It’s even worse because most of the students already have an idea of what math is engraved in their minds, and it’s difficult to change. Esp. those students who are forced to take calculus who do not need it.
即使当了三年助教,我仍然感到沮丧,因为我无法避免传递出这样一个强烈的信息:数学极其枯燥和机械。更糟糕的是,大多数学生心中已经根深蒂固地形成了对数学的固有认知,而这种认知很难改变。尤其是那些被迫学习微积分但实际上并不需要它的学生。
If I had the freedom to design my own course, I think I would start by making my textbook Paul Lockhart’s Measurement. It includes all “high-school” math from geometry to calculus, and is very focused on big picture arguments and specific, engaging proofs.
如果我有自由设计自己的课程,我会首先选择保罗·洛克哈特(Paul Lockhart)的《测量》(Measurement)作为教材。这本书涵盖了从几何学到微积分的所有“高中”数学内容,并且非常注重宏观的论证思路和具体、有趣的证明过程。
Btw, you might be interested in my more recent post on the State Standards in Mathematics.
顺便说一下,你可能会对我最近一篇关于《数学州立标准》的文章感兴趣。
gngl
March 5, 2014 at 5:04 pm Reply
“I think I have it. So if everybody had a different number of friends, then one person would have to have no friends and someone would have to be everyone’s friend, but that can’t happen.”
“我想我明白了。如果每个人的朋友数量都不同,那么必然有一个人没有朋友,而另一个人是所有人的朋友,但这是不可能的。”
That sounds nice, but for N friends, one could conceivably have 0, 1, 2, … , N-1 friends for each party-goer (unless further study excludes that), not necessarily 0…N, which means that this argument alone argument must be missing something.
这听起来很有道理,但对于 N 个参与者来说,每个人的朋友数量理论上可以是 0、1、2、……、N-1(除非有进一步的研究排除这种情况),而不一定是 0 到 N,这意味着仅靠这个论证还不够充分,一定遗漏了某些东西。
- gngl
March 5, 2014 at 5:12 pm Reply
Ah, scratch that, I’ve missed the loop. That’s what I get for drawing adjacency matrices instead of pictures! Although, on reflection, there’s a contradiction in the matrix as well (symmetry excludes it).
啊,算我没说,我忽略了循环的情况。这就是我只画邻接矩阵而不画图的后果!不过,仔细想想,邻接矩阵中也存在矛盾(对称性排除了这种情况)。
via:
- Teaching Mathematics – Graph Theory – Math ∩ Programming
https://jeremykun.wordpress.com/2011/06/26/teaching-mathematics-graph-theory/ - LockhartsLament.pdf – Mathematical Association of America
https://maa.org/devlin/LockhartsLament.pdf





















 6093
6093

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








