流体力学基本方程（篇 1）

注：本文为 “流体力学基本方程” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

---

计算流体力学三大基本方程推导

BertramZhang 于 2018-01-31 14:04:10 发布

基于安德森《计算流体力学基础》

连续性方程

原理

固定流体微元内的质量变化率等于流体从笛卡尔坐标三个方向的流出量代数和。

推导过程

1. 计算各方向的流体流出量增量：

   • x 方向：
     $$-\rho udydz+\left(\rho u+\frac{\partial \rho u}{\partial x}dx\right)dydz=\frac{\partial \rho u}{\partial x}dxdydz$$
   • y 方向：
     $$-\rho vdxdz+\left(\rho v+\frac{\partial \rho v}{\partial y}dy\right)dxdz=\frac{\partial \rho v}{\partial y}dxdydz$$
   • z 方向：
     $$-\rho wdxdy+\left(\rho w+\frac{\partial \rho w}{\partial z}dz\right)dxdy=\frac{\partial \rho w}{\partial z}dxdydz$$

2. 结合质量变化率关系：
   微元内质量变化率为：
   $$\frac{\partial \rho }{\partial t}dxdydz$$

   与三个方向的流出量增量之和相等，则：
   $$-\frac{\partial \rho }{\partial t}dxdydz=\frac{\partial \rho u}{\partial x}dxdydz+\frac{\partial \rho v}{\partial y}dxdydz+\frac{\partial \rho w}{\partial z}dxdydz$$
   整理得：
   $$\frac{\partial \rho }{\partial t}dxdydz+\frac{\partial \rho u}{\partial x}dxdydz+\frac{\partial \rho v}{\partial y}dxdydz+\frac{\partial \rho w}{\partial z}dxdydz=0$$

3. 最终形式：

   • 一般形式：
     $$\frac{\partial \rho }{\partial t}+\frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \rho w}{\partial z}=0$$
   • 散度表示：
     $$\frac{\partial \rho }{\partial t}+\text{div}(\rho \mathbf{U})=0$$
   • 不可压缩流体（密度 $\rho$ 为常数）：
     $$\text{div}(\mathbf{U})=0$$

动量方程（纳维-斯托克斯方程）

根据牛顿第二定律 $F=ma$，对流体微元推导如下：

方程式核心关系

• 左边（总作用力）：$F=$ 表面力 + 体积力
• 右边（动量变化率，仅 x 方向）：$ma=m\frac{Du}{Dt}=\rho \frac{Du}{Dt}dxdydz$

体积力表达式

$$\rho f_{x}dxdydz$$（$f_x$ 为 x 方向单位质量体积力）

表面力表达式（x 方向）

流体微元 x 方向所有正应力与切应力之和
$$\begin{array}{rl}-{\tau }_{xx}dydz& +\left({\tau }_{xx}+\frac{\partial {\tau }_{xx}}{\partial x}dx\right)dydz\\ -{\tau }_{xy}dxdz& +\left({\tau }_{xy}+\frac{\partial {\tau }_{xy}}{\partial y}dy\right)dxdz\\ -{\tau }_{xz}dxdy& +\left({\tau }_{xz}+\frac{\partial {\tau }_{xz}}{\partial z}dz\right)dxdy\\ & +\left[P-\left(P+\frac{\partial P}{\partial x}dx\right)\right]dydz\end{array}$$

${\tau }_{ij}$：$i$ 为应力方向，$j$ 为作用面法向，满足 ${\tau }_{ij}={\tau }_{ji}$。
${\tau }_{ij}={\tau }_{ji}$ 的本质是流体微元不能无限制旋转，是动量矩守恒的必然结果；其物理意义是“任意两个正交方向的交叉切应力大小相等”，这一特性让应力张量从 9 个独立分量减少到 6 个（3 个正应力+3 个切应力），大幅简化了纳维-斯托克斯方程的推导和求解。

表面力整理结果

$$\frac{\partial {\tau }_{xx}}{\partial x}dxdydz+\frac{\partial {\tau }_{xy}}{\partial y}dxdydz+\frac{\partial {\tau }_{xz}}{\partial z}dxdydz-\frac{\partial P}{\partial x}dxdydz$$

动量方程平衡关系

将体积力表达式、表面力表达式和方程右边表达式带入牛顿第二定律表达式中可得：
$$\rho \frac{Du}{Dt}dxdydz=\rho f_{x}dxdydz+\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}-\frac{\partial P}{\partial x}\right)dxdydz$$

化简后非守恒形式（分量式）

$$\rho \frac{Du}{Dt}=\rho f_x+\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}-\frac{\partial P}{\partial x}$$
同理可得 y 方向和 z 方向的两个方程：
$$\rho \frac{Dv}{Dt}=\rho f_y+\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}-\frac{\partial P}{\partial y}$$
$$\rho \frac{Dw}{Dt}=\rho f_z+\frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial y}+\frac{\partial {\tau }_{zz}}{\partial z}-\frac{\partial P}{\partial z}$$
注：$\frac{D}{Dt}=\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}+w\frac{\partial }{\partial z}$ 为物质导数。

守恒形式与非守恒形式的区别

守恒形式定义

若方程可写成控制方程通用形式：

$\frac{\partial (\rho \varphi )}{\partial t}+\nabla \cdot (\rho \mathbf{U}\varphi )=\nabla \cdot \left({\Gamma }_{\varphi }\nabla \varphi \right)+S_{\varphi }$

对流项采用散度形式，即为守恒型控制方程。…

变量说明：

• $\rho$：流体密度（标量）
• $\varphi$：通用求解变量（标量或向量分量，如质量、动量分量、温度等）
• $t$：时间（标量）
• $\nabla \cdot (\cdot )$：散度算子（描述物理量的通量净流出）
  • 注：div 和 ∇· 是散度算子的两种表示方式
• $\mathbf{U}$：流体速度向量（包含 $u,v,w$ 三个分量）
• ${\Gamma }_{\varphi }$：扩散系数（如动量对应 $\mu$，能量对应 $\alpha$）
• $\nabla \varphi$：通用变量 $\varphi$ 的梯度（向量）
  • 注：$\nabla \varphi$ 和 $\text{grad}\varphi$ 是“梯度算子”的两种表示方式
• $S_{\varphi }$：源项（单位体积内 $\varphi$ 的生成/消耗率）

扩散系数说明：
不同 $\varphi$ 对应不同扩散系数：

• $\varphi =1$（质量输运）：${\Gamma }_{\varphi }$ 为质量扩散系数
• $\varphi =u$（x 方向动量）：${\Gamma }_{\varphi }=\mu$（动力粘性系数）
• $\varphi =T$（温度）：${\Gamma }_{\varphi }=\alpha =k/(\rho c_p)$（热扩散系数）

该形式是流体力学中守恒型控制方程的标准通用表达式，涵盖质量、动量、能量等物理量的输运规律（对流输运+扩散输运+源项）。

从微元体角度，守恒型与非守恒型方程等价，但计算特殊流场（如湍流、激波）时差异显著。据《数值传热学》（第二版），湍流计算中守恒型方程结果光滑稳定，非守恒型易引发数值震荡；且仅守恒型方程能在有限大小控制容积内满足守恒定律。

推导动量方程的守恒形式

以 $x$ 方向为例展开推导：

1. $x$ 方向动量的物质导数展开

$x$ 方向动量的物质导数（跟随流体微元的变化率）可分解为局部变化率与对流变化率：
$$\rho \frac{Du}{Dt}=\rho \frac{\partial u}{\partial t}+\rho \mathbf{V}\cdot \nabla u$$
注：$\mathbf{V}$ 为流体速度向量，$\nabla u={\left(\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z}\right)}^T$ 是 $u$ 的梯度。

2. 利用乘积的偏导数法则

对 $\rho u$ 关于时间 $t$ 求偏导，由乘积求导法则得：
$$\frac{\partial (\rho u)}{\partial t}=\rho \frac{\partial u}{\partial t}+u\frac{\partial \rho }{\partial t}$$
移项后，得到 $x$ 方向动量局部变化率的表达式：
$$\rho \frac{\partial u}{\partial t}=-u\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial t}$$

3. 代入物质导数展开式

将上式代入物质导数的分解式，得：
$$\rho \frac{Du}{Dt}=-u\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial t}+\rho \mathbf{V}\cdot \nabla u$$

4. 应用散度的向量恒等式

对于标量与向量乘积的散度，有恒等式：
$$\rho \mathbf{V}\cdot \nabla u=\nabla \cdot (\rho u\mathbf{V})-u\nabla \cdot (\rho \mathbf{V}\text{（散度乘积法则）})$$

将其代入上式，得：

$$\begin{array}{rl}\rho \frac{Du}{Dt}& =-u\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\vec{V})-u\mathbf{V}\cdot \nabla \rho \\ \Rightarrow \rho \frac{Du}{Dt}& =-u\left(\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{V})\right)+\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\mathbf{V})\\ \Rightarrow \rho \frac{Du}{Dt}& =\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\mathbf{V})\end{array}$$

推导说明：

1. 第一步利用散度乘积法则（$\nabla \cdot (\varphi \vec{A})=\varphi \nabla \cdot \vec{A}+\vec{A}\cdot \nabla \varphi$），将 $\rho \mathbf{V}\cdot \nabla u$ 转换为散度形式；
2. 第二步代入物质导数定义（$\frac{Du}{Dt}=\frac{\partial u}{\partial t}+\mathbf{V}\cdot \nabla u$），结合乘积的时间偏导展开；
3. 第三步利用连续性方程（$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{V})=0$）消去零项，最终得到动量方程的守恒形式转换关系。

$$\begin{array}{rl}\rho \frac{D\mathbf{u}}{Dt}& =-\mathbf{u}\frac{\partial \rho }{\partial t}+\frac{\partial (\rho \mathbf{u})}{\partial t}+\nabla \cdot (\rho \mathbf{uv})-\mathbf{u}\nabla \cdot (\rho \mathbf{v})\\ \Rightarrow \rho \frac{D\mathbf{u}}{Dt}& =-\mathbf{u}\left(\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})\right)+\frac{\partial (\rho \mathbf{u})}{\partial t}+\nabla \cdot (\rho \mathbf{uv})\\ \Rightarrow \rho \frac{D\mathbf{u}}{Dt}& =\rho \frac{\partial \mathbf{u}}{\partial t}+\nabla \cdot (\rho \mathbf{uv})\end{array}$$

5. 结合连续方程化简

连续方程（质量守恒）为：
$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{V})=0$$
因此 $u\left(\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{V})\right)=0$，代入上式后化简得：
$$\rho \frac{Du}{Dt}=\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\mathbf{V})$$

6. 代入非守恒形式，得到 $x$ 方向守恒方程

将上式代入 $x$ 方向的非守恒动量方程，最终得到 $x$ 方向的守恒形式动量方程：
$$\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\mathbf{V})=\rho f_x+\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}-\frac{\partial P}{\partial x}$$

同理推导 $y$、$z$ 方向的守恒形式

• $y$ 方向守恒方程：
  $$\frac{\partial (\rho v)}{\partial t}+\nabla \cdot (\rho v\mathbf{V})=\rho f_y+\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}-\frac{\partial P}{\partial y}$$

• $z$ 方向守恒方程：
  $$\frac{\partial (\rho w)}{\partial t}+\nabla \cdot (\rho w\mathbf{V})=\rho f_z+\frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial y}+\frac{\partial {\tau }_{zz}}{\partial z}-\frac{\partial P}{\partial z}$$

动量方程的守恒形式总结

综合 $x$、$y$、$z$ 方向，动量方程的守恒形式为：
$$\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\mathbf{V})=\rho f_x+\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}-\frac{\partial P}{\partial x}$$

$$\frac{\partial (\rho v)}{\partial t}+\nabla \cdot (\rho v\mathbf{V})=\rho f_y+\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}-\frac{\partial P}{\partial y}$$

$$\frac{\partial (\rho w)}{\partial t}+\nabla \cdot (\rho w\mathbf{V})=\rho f_z+\frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial y}+\frac{\partial {\tau }_{zz}}{\partial z}-\frac{\partial P}{\partial z}$$

---

流体动力学控制方程（详细推导）

diyhoos 于 2018-07-06 18:16:00 发布

流体动力学控制方程是计算流体力学（CFD）的理论基础，基于三个基本物理学原理建立：质量守恒定律、牛顿第二定律、能量守恒定律。这些方程是所有流动现象必须遵循的数学描述，其推导依赖不同的控制体模型，具体包括固定/移动的有限控制体、固定/移动的无穷小控制体（流动微团），分别对应守恒型与非守恒型的积分方程或偏微分方程，其中守恒型偏微分方程更适用于CFD数值求解。

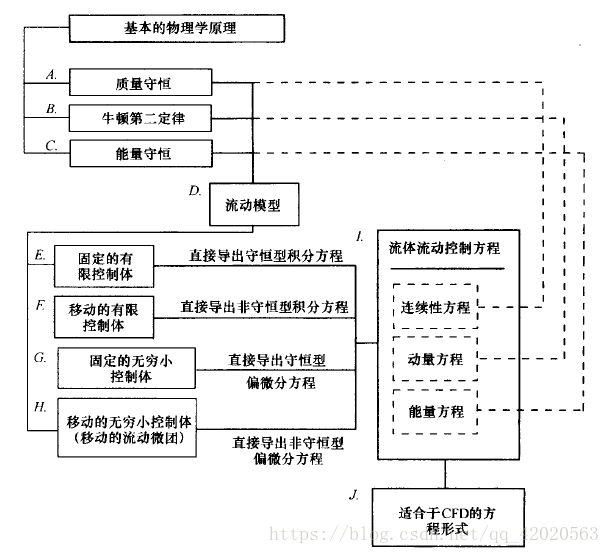
一、连续性方程

推导模型

选取直角坐标系 $oxyz$ 中固定不动的微平行六面体作为控制体，边长分别为 $dx,dy,dz$，基于质量守恒定律推导微分形式方程。

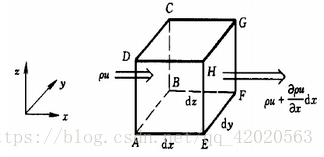
推导过程

1. 各方向质量通量分析

   • x 方向：流体从控制体左侧面 $ABCD$ 流入，流入质量通量为 $\rho u_{x}dydzdt$；从右侧面 $EFGH$ 流出，流出质量通量为 $\left[\rho u_x+\frac{\partial (\rho u_x)}{\partial x}dx\right]dydzdt$。
   • 该方向净流出质量为两者差值：$\frac{\partial (\rho u_x)}{\partial x}dxdydzdt$。
   • 同理，y 方向净流出质量：$\frac{\partial (\rho u_y)}{\partial y}dxdydzdt$；z 方向净流出质量：$\frac{\partial (\rho u_z)}{\partial z}dxdydzdt$。

2. 控制体内质量变化
   控制体密度随时间变化，$dt$ 时间内控制体内质量减少量为 $-\frac{\partial \rho }{\partial t}dxdydzdt$。

3. 质量守恒方程建立
   根据质量守恒定律，控制体的净流出质量等于体内质量减少量，即：
   $$\left[\frac{\partial (\rho u_x)}{\partial x}+\frac{\partial (\rho u_y)}{\partial y}+\frac{\partial (\rho u_z)}{\partial z}\right]dxdydzdt=-\frac{\partial \rho }{\partial t}dxdydzdt$$
   消去公共项 $dxdydzdt$，得到直角坐标系下连续性方程的微分形式：
   $$\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u_x)}{\partial x}+\frac{\partial (\rho u_y)}{\partial y}+\frac{\partial (\rho u_z)}{\partial z}=0$$

4. 散度形式表示
   引入散度算子 $\nabla \cdot (\rho \vec{u})=\frac{\partial (\rho u_x)}{\partial x}+\frac{\partial (\rho u_y)}{\partial y}+\frac{\partial (\rho u_z)}{\partial z}$，方程可简化为：
   $$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \vec{u})=0$$

二、动量守恒方程（纳维-斯托克斯方程）

推导依据

基于牛顿第二定律 $F=ma$，以运动流体微团为分析对象，将作用力与加速度沿 $x,y,z$ 轴分解，建立各方向标量方程。此处以 $x$ 方向为例进行推导。

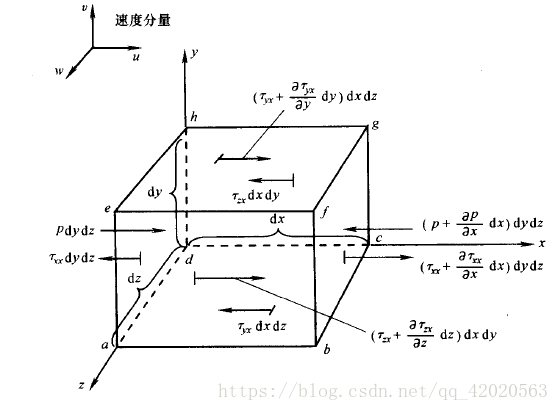
作用力分析

1. 体积力
   直接作用于流体微团整个体积的力（如重力、电场力、磁场力），单位质量流体的体积力在 $x$ 方向分量为 $f_x$。微团体积为 $dxdydz$，故 $x$ 方向体积力为 $\rho f_{x}dxdydz$。

2. 表面力
   由周围流体作用于微团表面的压力和粘性应力组成：

   • 压力：左侧面压力作用为 $pdydz$，右侧面压力作用为 $\left(p+\frac{\partial p}{\partial x}dx\right)dydz$，压力合力为 $-\frac{\partial p}{\partial x}dxdydz$。
   • 粘性应力：包括正应力和切应力，$x$ 方向粘性应力合力为 $\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}\right)dxdydz$，其中 ${\tau }_{xx}$ 为 $x$ 方向正应力，${\tau }_{yx}、{\tau }_{zx}$ 为不同方向切应力。

3. 加速度表达式
   流体微团质量固定，加速度为速度的物质导数。$x$ 方向速度分量为 $u$，加速度为：
   $$a_x=\frac{Du}{Dt}=\frac{\partial u}{\partial t}+(\vec{V}\cdot \nabla )u=\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}$$
   其中 $\frac{D}{Dt}$ 为物质导数，$\frac{\partial }{\partial t}$ 为当地导数，$(\vec{V}\cdot \nabla )$ 为迁移导数。

方程建立

联立牛顿第二定律 $F_x=m{a}_x$，代入作用力与加速度表达式，得 $x$ 方向动量方程：
$$\rho f_x-\frac{\partial p}{\partial x}+\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}=\rho \frac{Du}{Dt}$$

守恒形式转换

利用物质导数与连续性方程的关系 $\rho \frac{Du}{Dt}=\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\vec{V})$，代入上式得守恒形式（纳维-斯托克斯方程）：
$$\rho f_x-\frac{\partial p}{\partial x}+\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}=\frac{\partial (\rho u)}{\partial t}+\nabla \cdot (\rho u\vec{V})$$

同理可推导 $y,z$ 方向动量方程，形式与 $x$ 方向一致，仅需替换对应方向的速度分量、体积力分量及应力分量。

三、能量方程

推导原理

基于能量守恒定律，表述为：微元体内能量的变化率 = 进入微元体的净热流量 + 体积力与表面力对微元体做的功率（即 $A=B+C$）。

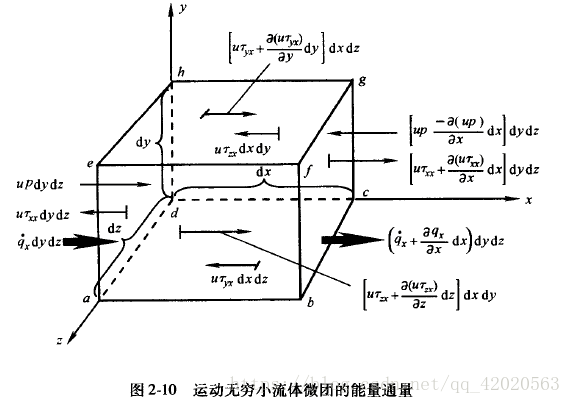
各物理量定义与计算

1. 微元体内能量变化率（$A$）
   流体微团的总能量包括单位质量内能 $e$ 和单位质量动能 $\frac{V^2}{2}$（$V$ 为速度大小），能量变化率由物质导数描述：
   $$A=\rho \frac{D}{Dt}\left(e+\frac{V^2}{2}\right)dxdydz$$

2. 进入微元体的净热流量（$B$）
   热流量来自两部分：体积加热（如辐射热）和热传导（傅里叶热传导定律）：

• 体积加热：单位质量体积加热率为 $\dot{q}$，贡献量为 $\rho \dot{q}dxdydz$。
• 热传导：热流密度与温度梯度成正比，热传导热流量为 $\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)dxdydz$，其中 $k$ 为热导率，$T$ 为温度。

综上，净热流量为：
$$B=\left[\rho \dot{q}+\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)\right]dxdydz$$

3. 体积力与表面力做功功率（$C$）

• 体积力做功功率：体积力 $\rho \vec{f}$ 与速度 $\vec{V}$ 的点积，即 $\rho \vec{f}\cdot \vec{V}dxdydz$。
• 表面力做功功率：各方向应力与对应速度分量的乘积及其空间变化率之和，$x$ 方向贡献为 $\left[-\frac{\partial (up)}{\partial x}+\frac{\partial (u{\tau }_{xx})}{\partial x}+\frac{\partial (u{\tau }_{yx})}{\partial y}+\frac{\partial (u{\tau }_{zx})}{\partial z}\right]dxdydz$，$y,z$ 方向同理。

能量方程最终形式

联立 $A=B+C$，消去动能项与体积力做功项，仅保留内能的物质导数，整理得：
$$\rho \frac{De}{Dt}=\rho \dot{q}+\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+\Phi -\nabla \cdot (p\vec{V})$$
其中 $\Phi$ 为粘性耗散项，表达式为：
$$\Phi ={\tau }_{xx}\frac{\partial u}{\partial x}+{\tau }_{yy}\frac{\partial v}{\partial y}+{\tau }_{zz}\frac{\partial w}{\partial z}+{\tau }_{xy}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+{\tau }_{yz}\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)+{\tau }_{zx}\left(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\right)$$

四、小结

流体动力学控制方程（连续性方程、动量方程、能量方程）是基于基本物理守恒定律的数学表达，其推导过程明确了各物理量的本质的作用机制。理解方程的物理意义、控制体假设及形式转换，是准确解读CFD数值求解结果的前提。

---

• 流体力学基本方程（篇 2）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/155062909

---

via:

• 计算流体力学三大基本方程：连续性方程、动量方程（纳维-斯托克斯方程）和能量方程推导-优快云博客
  https://blog.youkuaiyun.com/fanshuzai3/article/details/79190769
• 流体动力学控制方程（详细推导）_流体控制方程-优快云博客
  https://blog.youkuaiyun.com/qq_42020563/article/details/80940387