注: 本文为 “微积分演变展” 相关文章合辑。
未整理去重。
牛顿与莱布尔茨的微积分战争
杰森苏格拉底巴迪 算法与数学之美 2022年07月07日 20:32 北京
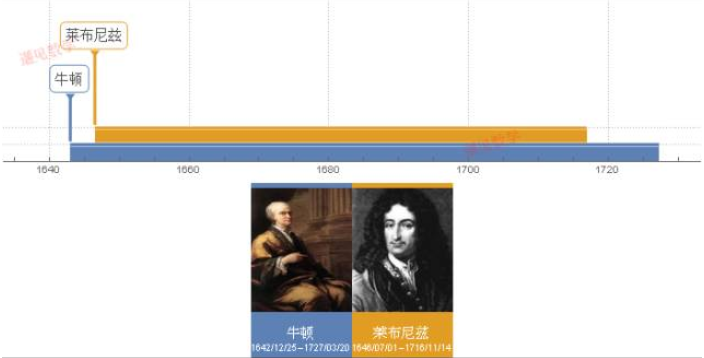
微积分第一发明人之争
十八世纪初,德国最伟大的数学家戈特弗里德・威廉・莱布尼茨(1646—1716)和英国最伟大的数学家艾萨克・牛顿爵士(1642—1726)之间即将爆发一场激烈的战争,这场战争持续超过 10 年,直到他们各自去世。
这场战争中,他们都宣称自己才是微积分的创立者。微积分是数学分析的基础,为我们提供了一套测算包括几何图形、行星绕太阳运行的轨迹在内的各种曲面面积的通用方法。微积分是十七世纪最伟大的知识遗产之一。牛顿在 1665 至 1666 年间(他创造力最强的一段时间)创立了这一数学方法。当时牛顿还是一名年轻的剑桥学生,他离开了老师和同学,回到自己的乡村住所。牛顿在乡下度过了两年几乎与世隔绝的生活,这段时间里,他不停地做实验,潜心于思考支配宇宙的物理法则。牛顿在这两年中创建的科学体系或许是其他任何一个科学家在同样短的时间内都无法完成的。他在几乎各个科学领域都有重大发现,如现代光学、流体力学、潮汐物理、运动定律、万有引力定律等。
最重要的是,牛顿创立了称之为流数法的微积分。但牛顿在其大半生的时间里,却并没有将这一发明公之于世,而仅仅是将自己的私人稿件在朋友之间传阅。牛顿直到发明微积分 10 年之后,才正式出版相关著作。
莱布尼茨则是在晚 10 年之后的 1675 年才发明微积分,那段时间是他最为多产的一个时期,当时他住在巴黎。莱布尼茨在接下来的十年里不断完善这一发现,创立了一套独特的微积分符号系统,并于 1684 年和 1686 年分别发表两篇关于微积分的论文。莱布尼茨虽晚于牛顿发明微积分,但他发表微积分的著作却早于牛顿。正是因为这两篇论文,莱布尼茨才得以宣称自己是微积分的第一创始人。微积分意义是如此重大,到 1700 年,莱布尼茨在整个欧洲被公认为是当时最伟大的数学家。
莱布尼茨和牛顿都说自己才是微积分真正的创始人,现在则普遍认为两人各自独立创立了微积分,都是微积分的发明人。微积分可算是自古希腊以来数学史上最大的进步,两人都为之做出了重大贡献。现代学者或许愿意共享这一巨大的荣耀,但是莱布尼茨和牛顿在发明微积分的归属权上却互不相让。十七世纪末,莱布尼茨和牛顿的支持者均指责对方行为不当。十八世纪的前二十年,微积分战争正式地爆发了。
莱布尼茨曾看过牛顿早期的研究,牛顿因此认定莱布尼茨剽窃了自己的成果,他开始最大限度地利用自己的声望来攻击莱布尼茨。牛顿声称莱布尼茨知道自己首先发明了微积分,他能证明这一点。依靠自己多年建立的巨大声望,牛顿指使亲信撰文攻击莱布尼茨。牛顿的支持者们暗示莱布尼茨偷窃了牛顿的理念,并帮着牛顿反驳各种回应和指责。牛顿这么做并非出于纯粹的恶意或嫉妒,而是他的确相信莱布尼茨偷窃了他的成果。在他看来,这场关于微积分的战争是恢复自己名誉以及夺回自己最重要的学术成果的好机会。
莱布尼茨也毫不退让,任何人都不会对这样的攻击置之不理。在支持者的帮助下,莱布尼茨奋起反击。莱布尼茨宣称事实的真相是牛顿借用了他的理念;他积极联络欧洲的学者们,一封接一封写了许多信为自己辩护。莱布尼茨还匿名发表了多篇为自己辩护以及攻击牛顿的文章。他甚至将争论引入到政府层面,甚至是英国国王那里。
微积分战争日趋激烈,牛顿和莱布尼茨以公开或秘密的形式相互攻击。他们要么请人代写评论,要么发表匿名文章。两人都是享誉欧洲的学者,都尽可能地利用各自的声望号召人们支持自己。当时的学者由此分成两个对立的阵营。两人都收集了大量的证据,写了大量证明自己观点的文章。每次读到对方的指控时两人都会怒不可遏。如果不是莱布尼茨在 1716 年去世,这场争端将会持续更久。在某种意义上,莱布尼茨的离世并未结束微积分战争,因为牛顿并未停止 “战斗”,仍继续发表攻击性的文章。
孰对孰错?牛顿似乎有充足的理由声称是他首先发明了微积分,并且成功地说服了人们。在牛顿去世时,不仅是英国,整个欧洲都承认他早于莱布尼茨发明微积分。
英国国家肖像馆至今还挂着一幅著名的牛顿肖像,这幅肖像是戈弗雷・内勒爵士 1702 年所画的。肖像描绘了一个中年男人,披着棕色学术袍,衣领却是蓝色的。在画像中,牛顿的眼睛显得又大又圆,还有些许眼袋。画家在他的脸颊,鼻子和额头上点缀粉色,他的脸色则有些泛蓝。经过这些色彩的渲染,牛顿的表情似乎显得不那么严峻了,但你仍然很难想象,画像中的人笑起来会是什么样。

牛顿
真相到底如何呢?牛顿确实比莱布尼茨早十年发明微积分,但这并不足以说明牛顿就是微积分的创立者。莱布尼茨同样有权争取微积分的创立权。莱布尼茨独立地发展了微积分。更重要的是,他首先发表了有关微积分的著作;他对微积分的研究比牛顿更加深入;他创立了远远优于牛顿的微积分符号,这些符号沿用至今。他花费数年时间将微积分发展成一个方便所有人使用的完整的数学架构。因此,我们可以这样说,莱布尼茨的微积分方法对数学史做出的贡献要大于牛顿。
莱布尼茨和牛顿如果在另一种情形下相遇,他们可能会成为朋友。他们阅读相同的书籍,研究的同样是当时最重大的数学和哲学问题。莱布尼茨与众多欧洲学者保持着稳定的通信关系,牛顿也是其中之一。但莱布尼茨和牛顿从未碰过面,他们之间的交流仅限于几封书信往来,年轻时有几封、中年一封,晚年更只有一封短信。但是,他们之间的通信前后跨越了几十年。

莱布尼茨
在微积分战争爆发之前,莱布尼茨和牛顿没有多少直接交流的机会,但他们对彼此的欣赏一直都溢于言表。或许正是因为堆砌了太多的溢美之词,在翻脸后彼此的攻击也就愈加刻薄。许多作家,包括史学家和传记作者,都认为微积分战争毫无意义,是不幸的,甚至很荒谬。为了赢得这场争论,莱布尼茨和牛顿后来变得无所不用其极,充分展示两人身上不好的一面。他们真实的另一面与人们心目中抱负远大、淡泊名利、勤奋、多产的天才形象很难联系起来。
话虽如此,微积分战争还是令后人着迷,因为牛顿和莱布尼茨上演了历史上最重大的知识产权斗争。牛顿和莱布尼茨,英国和德国数学界的两位元老和巨人,在这场激烈的战争中充分展示了他们卓越的才智、高傲的个性,甚至是疯狂的一面。但归根到底,这场战争让我们看到了人性的真实。
微积分是最重要的数学发明,极大推动了科学的进步。但在两位最伟大的科学巨匠 —— 牛顿和莱布尼茨之间,却爆发了激烈的微积分发明权之争。在各自拥趸的支持与撺掇之下,他们相互发难,指责对方是剽窃者。
这场旷日持久的微积分战争,是科学史上的重大事件,是损失无法估量的悲剧。
谁胜谁负(1716—1728)
莱布尼茨生命中最后的日子是在汉诺威度过的,而这段时间乔治和他的大臣们则一直待在英格兰。也许这说明乔治疏远了莱布尼茨,至少是不那么支持他了。发生在 1711 年的一件事或许更能说明他们之间的关系。这一年莱布尼茨不慎摔伤了。他已是一位体弱多病、身有残疾的老人。据说乔治并没有表现出特别的关心,甚至把这件事当成一个笑话。显然乔治对一个长期为其家族服务的老人缺乏应有的同情心。
这次受伤只不过是莱布尼茨在生命的最后几年里所要承受的一长串伤痛之一。莱布尼茨患有痛风症,这是一种给人带来巨大痛苦的关节炎症,会引起关节发炎和锥刺般的疼痛,这种痛苦往往要好几天才能减缓。在莱布尼茨生命的最后关头,他的痛风症愈加严重了。莱布尼茨于 1715 年写道:“我的脚经常疼得难以忍受,手有时也会胀痛。但感谢上帝,我的头部和胃仍然是健康的。”
到后来,或许是缺乏运动的缘故,莱布尼茨的右腿上长了可怕的脓肿,这使他无法正常行走。不过,莱布尼茨从未屈从于疾病。为了对付痛风,他让自己平躺在床上,用木头钳子紧夹发炎的关节。不幸的是,这种做法明显对他的神经造成了严重的损害,最后不得不长期卧床,几乎丧失了行走能力。
1716 年 11 月 13 日是一个星期五,莱布尼茨卧床八天后,终于同意接受一位名叫塞普的医生的治疗。史料记载为我们留下一幅有趣的画面:塞普医生发现自己遇到的病人是一部 “活的百科全书”,对艺术和医学应用都有深入的了解。这位病人不顾自己脉搏衰弱、病痛缠身,仍和前来看诊的医生大谈炼金术和历史。莱布尼茨的额头冒着冷汗,身体无法抑制地抖动着,周围放满了书籍和笔记。虽然还想工作,但此时他已经连笔都拿不起来了。
医生对莱布尼茨病情的预测是悲观的:他不可能再康复了。医生开了一些药,莱布尼茨勉强撑过了第二天。1716 年 11 月 14 日,这位闻名于世的莱比锡之子在他长期居住的汉诺威的寓所与世长辞了。
莱布尼茨并没有为自己的后事做过多的安排,棺木要临时购置。他的秘书艾克哈特订购了一副装饰华丽的棺椁,上面有贺拉斯的诗句以及数学与重生的符号。几天之后,莱布尼茨的遗体被转移到纽斯塔德特教堂,并在此举行了葬礼。莱布尼茨被安葬在纽斯塔德特教堂之内,在当时这是一种普通人享受不到的殊荣。
莱布尼茨去世以后,他的声望越来越大。在十八世纪,莱布尼茨就公认是一位非常重要的学者。1780 年,人们为了纪念他而专门建立了一座纪念牌。这是另一项不是贵族的人难以享有的殊荣。莱布尼茨的纪念牌被设计成一个圆形神庙的形状,神庙的中间树立着他的白色大理石半身雕像,上面刻着他的名字 “奥萨・莱布尼茨”。另一件事也可以反映出他在人们心目中的地位。多年以后,当人们翻修纽斯塔德特教堂时,教堂内其他人的遗骸都被搬迁到了别处,唯有莱布尼茨的遗骨被保留了下来,重新葬在了翻新的教堂之内。
尽管如此,许多历史学家都注意到了莱布尼茨有些寒酸的葬礼。约翰・克尔,他是克斯兰德人,在莱布尼茨去世的那天正好来到莱布尼茨居住的小镇。他惊奇地发现当地人对莱布尼茨并未给予足够的重视。他这样记述莱布尼茨的葬礼:“显然,人们更像是为一位寻常的小偷,而不是为一位给他们的祖国带来巨大荣耀的人举办葬礼。”
当时,乔治一世及其大部分朝臣都待在伦敦。国王是在王宫附近狩猎时听到莱布尼茨去世的消息的。历史记载,尽管整个宫廷都被邀请出席莱布尼茨的葬礼,但宫廷中最尊贵的人物,乔治一世本人,却没有到场。
由于莱布尼茨在欧洲享有的巨大声望,他去世之后,人们发表了多个讣告。《学者》杂志于 1717 年详细介绍了莱布尼茨的死讯和葬礼。1718 年海牙的一份刊物登载了以 “纪念历史性的莱布尼茨” 为题的文章。1717 年法国科学院在巴黎召开了大会,在会上科学院秘书长亲自诵读了致莱布尼茨的悼词。
莱布尼茨虽然是英国皇家学会的会员,但皇家学会并没有特别关注莱布尼茨的逝世。一个更大的侮辱是柏林科学学会没有任何纪念活动。要知道,莱布尼茨是柏林科学学会的创始人和首任主席。
莱布尼茨去世后不久,孔蒂神父写信给牛顿通知这一讯息。“莱布尼茨先生去世了,” 孔蒂在信中写道,“你们之间的争论终于可以结束了。” 但对于牛顿而言,这场争论并没有结束。
当牛顿得知莱布尼茨的死讯后,他再次出版了拉夫逊的著作,并在重版著作中插入了自己对莱布尼茨来信的回应。甚至在莱布尼茨死后,牛顿对自己主要竞争对手的恶感也没有随着时间的流逝而减弱。莱布尼茨过世两年之后,牛顿写了一篇长文,文章的主旨是以得意口吻夸耀,在自己有力的诘问下,莱布尼茨是如何变得理屈词穷的。莱布尼茨去世许多年后,牛顿仍在写针对他的挖苦信件和文章。当然,这类信件都是牛顿的私人物品,直到他去世十年之后才被人发现。
牛顿去世之后,他私藏的信件揭示了整个事件(他和莱布尼茨的争论)让他觉得有多么委屈,他认为自己遭受了莱布尼茨不公正的对待。牛顿坚称,莱布尼茨一直到死都是一个强盗和攻击者,而他自己,牛顿,才是学术抄袭的受害者和正当防卫者。牛顿坚持认为,任何事情都只能有一个真正的发明人 —— 即使有人在一定程度上改进了该发明。
在宣扬自己的伟大和打击对手上,牛顿和他的追随者们干得相当出色。众所周知,牛顿最著名的支持者是法国思想家伏尔泰。伏尔泰在英国生活过几年,回国之后,他写了大量盛赞牛顿及其理论的文章,他是第一个在法国大规模宣传英国人观点的人。而伏尔泰对待莱布尼茨及其学说则持严厉的批评态度,即使在这位 “前辈” 去世多年以后。伏尔泰在他的小说《老实人》中对莱布尼茨极尽讽刺和嘲笑,将后者称作愚蠢的潘格洛斯博士。即使面临死亡,潘格洛斯博士也声称这是 “所有可能世界中最好的世界”。伏尔泰无疑过分简化了莱布尼茨观点。
莱布尼茨建立了一种理论,认为想要完全排除这个世界的邪恶是不可能的,但由于可以将邪恶降低到最小的程度,人们的确是生活在可能存在的最好的世界中。莱布尼茨并没有说 “所有可能世界中最好的世界” 在任何方面都是完美无缺的。他本人经历了太多的战争和痛苦,因此不会轻易否定一切事物。他的本意是,在无限多可能的世界中,我们生活的世界是最好的世界。在莱布尼茨看来,这个世界的痛苦和恐惧是一种仍然和谐的更高秩序的一部分。不仅如此,他认为由于造物主是完美的,为了有所区别,造物主所创造的世界一定是不完美的。
虽然莱布尼茨的理论遭受了伏尔泰的嘲讽,但伯特兰・罗素却持有相反的观点。罗素认为莱布尼茨构建了一个完整、合乎逻辑的理论体系,并就其理论专门写过一篇详尽的分析文章。然而,在莱布尼茨死后,无论他受到罗素怎样的推崇,也无论 “所有可能世界中最好的世界” 这一观点有多么朴素典雅,莱布尼茨的思想给人们留下的永远是好莱坞式简单直接的印象。自 18 世纪起,“所有可能世界中最好的世界” 这句话几乎成为莱布尼茨的反对者用来否定他的最常用的武器。莱布尼茨给人造成的印象是他过于乐观了,这种印象直到今天仍会对他本人及其学说产生不利的影响。用一名历史学家讽刺的话来说,莱布尼茨是所有可能的世界中 “最出色的学者”。
伏尔泰的嘲讽并不是莱布尼茨遭受的唯一打击。因为与牛顿的争论以及反对约翰・洛克(这两人都是英国的国家英雄),莱布尼茨在去世之后整整一个世纪都为英国人所憎恶。
牛顿在与莱布尼茨的微积分战争中坚持到了最后,他比后者多活了十年。牛顿在暮年时,已经成了一位在国际上享有巨大声誉的著名科学家。在牛顿最后的岁月里,他常常要接待来自国内外众多的学者、名流、巨富。牛顿是人们心目中的英雄,来访者把与这位有史以来最伟大的思想家的会面视作他们一生的荣耀。一些拜访过他的学者回到了欧洲,在那里他们继续支持牛顿的学说。
在牛顿人生的最后十年,《光学》和《原理》为他赢得了越来越大的声誉。牛顿亲自监督了新版本的出版。十八世纪二十年代,整个欧洲大陆开始广泛地翻译牛顿的著作,并给予这些著作极高的评价。尽管十七世纪英国和荷兰之间不止一次爆发过战争,但牛顿的著作却首先在荷兰受到推崇。荷兰的奥兰治亲王威廉登上英国王位,极大缓和了两国间的关系。
赫尔曼・布尔哈夫是一名荷兰医生,毕业于莱顿大学。他是牛顿学说的坚定支持者和热心传播者。布尔哈夫将牛顿称作 “哲学家中的王子”。牛顿另一个狂热的支持者是威廉・雅各布・格雷夫山德,他为牛顿理论在荷兰传播做了大量工作,被人称作 “了不起的宣传员格雷夫山德”。格雷夫山德也就读于莱顿大学,这在很大程度上要感谢牛顿,是牛顿在 1717 年帮他获得了在这所学校就读的机会。
尽管牛顿的《光学》对笛卡尔的光学理论构成了重大威胁,法国与英国爆发过多次战争,长期敌对,牛顿仍然越来越受到法国科学界的重视。牛顿与法国反对者之间的紧张关系在 1715 年得到了缓解。由于当年发生的日食只能在英国看到,一批杰出的法国学者从巴黎来到了伦敦。牛顿对法国客人的到来表示热情的欢迎,并安排他们参观了自己的光学实验。此后牛顿还帮助其中大部分人成功地当选为皇家学会会员。参访团中一位成员,为了表示他对牛顿衷心的感谢,回国后给牛顿寄去了五十瓶上等的法国香槟。
牛顿曾提出这样一种理论,地球不是一个完美的球体,而是一个两极略扁的椭圆球体。当牛顿的这一理论最终得到证实后,法国科学界对他的态度逐渐友好起来。1736 年,皮埃尔 - 路易・莫罗・德・莫佩尔蒂在位于北极圈内的芬兰拉普兰德测量了子午线弧度。莫佩尔蒂精准的测量证实了牛顿理论的正确性,此后他成为牛顿在法国最坚定的支持者之一。人们甚至将他称为艾萨克・莫佩尔蒂爵士。到 1784 年,牛顿在法国已经拥有了巨大的声誉。人们甚至举办了好几次为牛顿设计纪念碑的比赛。法国建筑科学院举办过一次设计比赛,声称这次设计是为了 “纪念我们这一时代最伟大的天才,设计不应仅仅注重宏伟华丽的风格,还要兼顾逝者所独有的高贵、庄重、朴素的气质”。
如同爱因斯坦是二十世纪天才的代表一样,十八世纪的人们将科学、发现以及其他与天才有关的一切抽象概念都集中到牛顿身上。不仅如此,一直到现代,牛顿仍在人们心目中享有崇高的地位。牛顿的形象广泛地出现在整个十八世纪的绘画、雕塑和艺术形式之中。建于 1755 年 7 月 4 日,如今位于剑桥大学校园内的牛顿雕像或许是他的众多雕像中最有名的一座了。牛顿被置于一个基座之上,身着宽松的长袍,手持棱镜,仰头上望。
当时的欧洲富人常常会定制牛顿的半身像,并将半身像置于壁炉或其他显眼地方用以展示。不仅如此,人们还经常将牛顿的头像放在自己肖像旁边作为背景。本杰明・富兰克林就有一幅这样的肖像画。
人们不仅仅是通过艺术,还在文学作品中对牛顿加以称颂。有人认为约瑟夫 - 路易・拉格朗日是十八世纪最伟大的数学家,拉格朗日认为,与其做出的成就相比,牛顿是人类有史以来最伟大也最幸运的学者。詹姆斯・汤姆森写了一首《致艾萨克爵士的诗歌》,在这首诗中他将牛顿描绘成洞悉一切的圣人。诗中有这样的句子:“牛顿伟大的灵魂离开了我们生活的星球 / 与繁星和神灵并列于苍穹之中 / 人们用沉默表达对他的敬意 / 光荣归于这个伟大的名字。” 伏尔泰说得更加简单:“牛顿是有史以来最伟大的人。”
…………
牛顿去世时,他的财产价值高达 3.2 万英镑,他将这笔财产留给了与他关系最近的亲人,他的侄子和侄女们。然而,比这笔巨大的有形资产更珍贵的是他的名声。牛顿在去世前已经成为一个受到各界名流追捧崇拜的活的传奇。在他离世的 1727 年,他的声望已经到达了最顶峰,他唯一没有体验过的事情或许就是死亡了。
1727 年 2 月底,牛顿到伦敦最后一次主持皇家学会会议,这次会议之后,死亡很快就降临了。牛顿看上去很健康,他自己显然也觉得身体状况良好。他告诉自己的侄女婿康杜伊特,他每天要睡九个小时。
然而,到了 3 月 3 日星期五,牛顿突然感到身体不适,不得不回家休息。不幸的是,一直到一个星期之后他才接受医生的治疗。3 月 11 日,康杜伊特听说了牛顿生病的消息,派人请来了米德医生和切斯尔顿医生。两位医生在牛顿的膀胱中发现了结石,这些结石使牛顿在其生命最后的几天遭受了巨大的痛苦。尽管遭受着剧烈的疼痛,牛顿仍然保持乐观的情绪。疼痛让他满头大汗,他仍与来访者谈笑风生。在接下来的一个星期里,牛顿的病情似乎略有好转,到 3 月 18 日星期六,他已经能够自己读报纸了。此时牛顿康复的可能性似乎越来越大。
但在当天晚上,牛顿失去了知觉,到了第二天,情况越来越糟。他的病情开始逐渐恶化,在与病魔进行了多个小时的斗争后,到 1727 年 3 月 20 日凌晨 1 点,牛顿终于与世长辞了。
本文选自《谁是剽窃者:牛顿与莱布尼茨的微积分战争》杰森・苏格拉底・巴迪 著,张菀 齐蒙 译
上海社会科学院出版社 2017 年 6 月出版
牛顿和莱布尼茨创立的微积分的异同点
牛顿的 “流数术”
牛顿 (I.Newton,1642-1727) 1642 年生于英格兰伍尔索普村的一个农民家庭。1661 年牛顿进入剑桥大学三一学院,受教于巴罗。笛卡儿的《几何学》和沃利斯的《无穷算术》,这两部著作引导牛顿走上了创立微积分之路。
牛顿于 1664 年秋开始研究微积分问题,在家乡躲避瘟疫期间取得了突破性进展。1666 年牛顿将其前两年的研究成果整理成一篇总结性论文 —《流数简论》,这也是历史上第一篇系统的微积分文献。在简论中,牛顿以运动学为背景提出了微积分的基本问题,发明了 “正流数术”(微分);从确定面积的变化率入手通过反微分计算面积,又建立了 “反流数术”;并将面积计算与求切线问题的互逆关系作为一般规律明确地揭示出来,将其作为微积分普遍算法的基础论述了 “微积分基本定理”。
这样,牛顿就以正、反流数术亦即微分和积分,将自古以来求解无穷小问题的各种方法和特殊技巧有机地统一起来。正是在这种意义下,牛顿创立了微积分。
牛顿对于发表自己的科学著作持非常谨慎的态度。1687 年,牛顿出版了他的力学巨著《自然哲学的数学原理》,这部著作中包含他的微积分学说,也是牛顿微积分学说的最早的公开表述,因此该巨著成为数学史上划时代的著作。而他的微积分论文直到 18 世纪初才在朋友的再三催促下相继发表。

莱布尼茨的微积分工作
莱布尼茨 (W.Leibniz,1646-1716) 出生于德国莱比锡一个教授家庭,青少年时期受到良好的教育。1672 年至 1676 年,莱布尼茨作为梅因茨选帝侯的大使在巴黎工作。这四年成为莱布尼茨科学生涯的最宝贵时间,微积分的创立等许多重大的成就都是在这一时期完成或奠定了基础。
1684 年,莱布尼茨整理、概括自己 1673 年以来微积分研究的成果,在《教师学报》上发表了第一篇微分学论文《一种求极大值与极小值以及求切线的新方法》(简称《新方法》),它包含了微分记号以及函数和、差、积、商、乘幂与方根的微分法则,还包含了微分法在求极值、拐点以及光学等方面的广泛应用。1686 年,莱布尼茨又发表了他的第一篇积分学论文,这篇论文初步论述了积分或求积问题与微分或切线问题的互逆关系,包含积分符号并给出了摆线方程:
莱布尼茨对微积分学基础的解释和牛顿一样也是含混不清的,有时他的是有穷量,有时又是小于任何指定的量,但不是零。

积分符号 ∫ ∫ ∫ 的由来
现在使用的积分符号 ∫ ∫ ∫ 是由莱布尼茨最早在 1675 1675 1675 年引入的。 ∫ ∫ ∫ 符号源于拉丁文单词 “ s u m m a ” “summa” “summa” ,意为“和”或“总和”。
在拉丁文中,字母 S S S 代表 “ s u m m a ” “summa” “summa” 。莱布尼茨选择了一个长得像 S S S 的符号来表示积分,突出了积分是一个求和的过程。
牛顿和莱布尼兹各自独立创立了微积分
牛顿和莱布尼茨就微积分的创立而言,尽管二者在背景、方法和形式上存在差异、各有特色,但二者的功绩是相当的。然而,一个局外人的一本小册子却引起了 “科学史上最不幸的一章”:微积分发明优先权的争论。瑞士数学家德丢勒在这本小册子中认为,莱布尼茨的微积分工作从牛顿那里有所借鉴,进一步莱布尼茨又被英国数学家指责为剽窃者。这样就造成了支持莱布尼茨的欧陆数学家和支持牛顿的英国数学家两派的不和,甚至互相尖锐地攻击对方。这件事的结果,使得两派数学家在数学的发展上分道扬镳,停止了思想交换。
在牛顿和莱布尼茨二人死后很久,事情终于得到澄清,调查证实两人确实是相互独立地完成了微积分的发明,就发明时间而言,牛顿早于莱布尼茨;就发表时间而言,莱布尼茨先于牛顿。
“微积分基本定理” 也称为牛顿 — 莱布尼茨定理,牛顿和莱布尼茨各自独立地发现了这一定理。微积分基本定理是微积分中最重要的定理,它建立了微分和积分之间的联系,指出微分和积分互为逆运算。

严格微积分的奠基者:柯西和魏尔斯特拉斯
先驱的努力
微积分学创立以后,由于运算的完整性和应用的广泛性,使微积分学成了研究自然科学的有力工具。但微积分学中的许多概念都没有精确的定义,特别是对微积分的基础 — 无穷小概念的解释不明确,在运算中时而为零,时而非零,出现了逻辑上的困境。
多方面的批评和攻击没有使数学家们放弃微积分,相反却激起了数学家们为建立微积分的严格而努力。从而也掀起了微积分乃至整个分析的严格化运动。
18 世纪,欧陆数学家们力图以代数化的途径来克服微积分基础的困难,这方面的主要代表人物是达朗贝尔 (d’Alembert,1717-1783)、欧拉和拉格朗日。达朗贝尔定性地给出了极限的定义,并将它作为微积分的基础,他认为微分运算 “仅仅在于从代数上确定我们已通过线段来表达的比的极限”;欧拉提出了关于无限小的不同阶零的理论;拉格朗日也承认微积分可以在极限理论的基础上建立起来,但他主张用泰勒级数来定义导数,并由此给出我们现在所谓的拉哥朗日中值定理。欧拉和拉格朗日在分析中引入了形式化观点,而达朗贝尔的极限观点则为微积分的严格化提供了合理内核。
微积分的严格化工作经过近一个世纪的尝试,到 19 世纪初已开始见成效。首先是捷克数学家波尔察诺 (B. Bolzano,1781-1848) 1817 年发表的论文《纯粹分析证明》,其中包含了函数连续性、导数等概念的合适定义、有界实数集的确界存在性定理、序列收敛的条件以及连续函数中值定理的证明等内容。
柯西对严格微积分的贡献
19 世纪分析的严密性真正有影响的先驱则是法国数学家柯西 (A-L.Cauchy,1789-1857)。从 1821 年到 1829 年,柯西相继出版了《分析教程》、《无穷小计算教程》以及《微分计算教程》,它们以分析的严格化为目标,对微积分的一系列基本概念给出了明确的定义,在此基础上,柯西严格地表述并证明了微积分基本定理、中值定理等一系列重要定理,定义了级数的收敛性,研究了级数收敛的条件等,他的许多定义和论述已经非常接近于微积分的现代形式。柯西的工作在一定程度上澄清了微积分基础问题上长期存在的混乱,向分析的全面严格化迈出了关键的一步。
然而,柯西的理论只能说是 “比较严格”,不久人们便发现柯西的理论实际上也存在漏洞。比如柯西定义极限为:“当同一变量逐次所取的值无限趋向于一个固定的值,最终使它的值与该定值的差可以随意小,那么这个定值就称为所有其它值的极限”,其中 “无限趋向于”、“可以随意小” 等语言只是极限概念的直觉的、定性的描述,缺乏定量的分析,这种语言在其它概念和结论中也多次出现。
应该指出,微积分计算是在实数领域中进行的,但到 19 世纪中叶,实数仍没有明确的定义,对实数系仍缺乏充分的理解,而在微积分的计算中,数学家们却依靠了假设:任何无理数都能用有理数来任意逼近。当时,还有一个普遍持有的错误观念就是认为凡是连续函数都是可微的。基于此,柯西时代就不可能真正为微积分奠定牢固的基础。所有这些问题都摆在当时的数学家们面前。
威尔斯特拉斯之严格微积分
另一位为微积分的严密性做出卓越贡献的是德国数学家魏尔斯特拉斯。他定量地给出了极限概念的定义,这就是今天极限论中的 “ε-δ” 方法。魏尔斯特拉斯用他创造的这一套语言重新定义了微积分中的一系列重要概念,特别地,他引进的一致收敛性概念消除了以往微积分中不断出现的各种异议和混乱。
另外,魏尔斯特拉斯认为实数是全部分析的本源,要使分析严格化,就先要使实数系本身严格化。而实数又可按照严密的推理归结为整数。因此,分析的所有概念便可由整数导出。这就是魏尔斯特拉斯所倡导的 “分析算术化” 纲领。基于魏尔斯特拉斯在分析严格化方面的贡献,在数学史上,他获得了 “现代分析之父” 的称号。
1857 年,魏尔斯特拉斯在课堂上给出了第一个严格的实数定义,但他没有发表。1872 年,戴德金 (R. Dedekind, 1831-1916)、康托尔 (B. Cantor,1829-1920) 几乎同时发表了他们的实数理论,并用各自的实数定义严格地证明了实数系的完备性。这标志着由魏尔斯特拉斯倡导的分析算术化运动大致宣告完成。
从以上介绍,可知微积分发展的历史轨迹是:
积分学—微分学—微积分学—极限理论—实数理论
但从数学分析课程来看,它的理论体系应该是:
实数理论—极限理论—微分学—积分学—微积分学
结论
牛顿和莱布尼兹两人独自创立了微积分,柯西和威尔斯特拉斯使严格微积分诞生。
参考资料
- History of the Calculus: The Origins of Cauchy’s Rigorous Calculus. Judith V. Grabiner. MIT Press, Cambridge, Mass., 1981.
篇外:
微积分的前奏:从列奥纳多到哈里奥特
原创 史迪威 图灵新知 2025年05月30日 11:00 北京
微积分是一个演算系统。它计算几何中的量,如斜率、长度和面积,以及力学中的量,如速度、加速度和能量。并且已经成功地解决了几何中的经典问题。
事实上,早期的微积分在很大程度上是代数几何的推广,新的演算方法逐渐有了自己的生命力。本节摘自**《证明的故事》**,讲述微积分的前奏:从列奥纳多到哈里奥特。
《证明的故事》,从古希腊几何学时代开始,涵盖代数、微积分、集合、数论、拓扑、逻辑等几乎全部数学分支中的证明故事。这本书不是教材,它是在讲数学的历史,更是在讲数学思想的演变。
作者数学史泰斗约翰·史迪威揭示了数学学习和研究的底层方法和逻辑,让读者看到在数学中什么定理可以被证明,如何证明?什么问题可以(或无法)被解决?为数学研究和发展打开全新的视角。
来源 | 《证明的故事:从勾股定理到现代数学》
作者 | [澳] 约翰·史迪威
译者 | 程晓亮 张浩
01 微积分的前奏
代数从三个具体方面推动了微积分的发展:
●提供了用于研究几何对象的坐标系和方程组;
● 将代数推广到“无穷多项式”(牛顿的幂级数微积分,据他说,灵感来自无限小数的计算);
● 提出无穷小量的代数和几何(莱布尼茨)。
无穷小量遭到了哲学家霍布斯和贝克莱(Berkeley)的批评,事实上,他们的批评直到极限概念在19世纪形成之后才得到合适的回应。
但在17世纪,也许和现在一样,大多数数学家认为基础是可靠的(当时这多亏了穷竭法),所以他们不愿花时间检查它们。这引发了一场缓慢发展的“基础危机”,直到19世纪末,这场危机才爆发。
本节是微积分的前奏,涉及无穷几何过程及其极限。它不是微积分,因为它不涉及一般的演算方法,但它展示了两个现在被认为是微积分问题的精巧解法。
第一个是圆的面积和周长,解法是列奥纳多·达·芬奇(Leonardo da Vinci)在1500年前后给出的;
第二个是第5.3节提到过的等角螺线的弧长,解法是托马斯·哈里奥特在1590年前后给出的。
02 圆的面积和周长
现在大家都知道,半径为r的圆的周长是2πr,面积是πr2。达·芬奇使用了一个简单的论证,展示了两者之间的关系,如图6.1所示(达·芬奇关于这个想法的草图可以在Codex Atlanticus 网站的第518页右页找到)。

达·芬奇想象把圆切成相同的小三角形。当这些三角形如图并排放置时,它们的高度接近r,而它们的总宽度接近圆的周长2πr。不可否认,这些“三角形”并不是真正的三角形,因为它们的底是一段圆弧。然而,当这些三角形越来越瘦时,近似值就变得越来越接近真实值。因此,在“极限情况”下,三角形的总面积,即圆的面积变成

03 等角螺线的弧长
等角螺线是在第5.3节中作为一个非代数曲线的例子介绍的。然而,它有一个非常简单的几何描述——半径向量与曲线形成的角为定值——并且由这个描述导出了一个同样简单的确定其弧长的方法。哈里奥特在1590年前后得到这个发现,但没有发表。洛纳在1979年的一本书里揭示了这个发现。图6.2展示了哈里奥特的想法。

哈里奥特从一个底角为α的等腰三角形开始,如图6.2左侧所示,将其切片得到相似的梯形。由于这些梯形是相似的,当每个梯形被它的对角线再切成两部分时,我们得到两个相似的三角形。然后将得到的三角形重新组合成图6.2右侧所示的多边形螺线。
这条螺线的边界涂成了红色,它包含这个等腰三角形的两条相等的边。从以下意义上讲,这条红色螺线是等角的:从三角形的公共顶点出发的线,每隔一条线与螺线形成的角都是α,螺线的长度等于等腰三角形两条红色边的长度之和。这个事实与梯形的高度无关。
现在,如果我们让梯形高度趋近于零,那么多边形螺线趋近一条光滑的等角螺线,其弧长等于等腰三角形两条红色边的长度之和。
我们在第2.7节中看到,欧几里得对有穷和无穷几何级数都有清晰的理解,并且发现四面体的体积是一个无穷几何级数的和。直到中世纪,人们才开始研究个全新的无穷级数——调和级数,并且直到17世纪,无穷级数(和其他无穷过程)才真正开始剧增。
本章我们主要关注17世纪的证明方法,即便这些方法按照后来的标准来看并不严格,但它们可以严格化,就像希尔伯特将欧几里得的几何公理严格化。但是,使17世纪的微积分严格化不仅仅是关于新公理的问题,更是关于新概念的问题,这些概念最好留到后面的章节介绍。
与此同时,我们应该认识到17世纪的方法是多么地卓有成效。那些数学家知道他们正在做正确的事情,尽管他们无法确切地解释在做什么。
何为微积分?
原创 王海华 模型视角 2024年08月28日 11:30 上海
何为“微积分”?
一方面,微积分是一种思维方式——动态的思维方式;另一方面,就内容而言,微积分是关于无穷小变量分析的数学。
上述解释来自奥斯卡·E·费尔南德。我觉得这个说法非常精辟、直抵微积分的核心。初学者如果在学习和应用微积分时从上述角度理解,我相信可以少走很多弯路。
从静态到动态
在微积分诞生之前,数学的世界是一个静态的世界。我们所熟知的代数和几何处理的都是不变的、固定的量。比方说,当我们计算一个边长为2米的正方形的周长时,我们很自然地套用公式:周长等于边长的四倍。这是一个经典的静态问题,答案很简单,周长就是8米。
但是,如果这个正方形的边长开始以每秒2米的速度增长,它的周长如何变化呢?这个看似简单的问题,在静态数学的世界里却无法解决。
微积分,正是为了解决类似动态问题而生的。
变是微积分的本质。
再举一个例子,如何计算一个球体的体积?微积分的思维不是直接套用公式 (实际上这只是结果),而是将这个球体切割成无数个极薄的圆盘,然后计算这些圆盘体积的总和。当圆盘的厚度趋于无穷小时,所有圆盘体积的总和就是球体的体积。

这种方法不仅更为灵活,还能解决许多以往数学无法触及的问题,比如不规则形体的体积计算。
要把微积分这个词当成动词来看。
研究无穷小量
无穷小是微积分的精髓所在,它指的是一种能够无限逼近于零,但永远不等于零的量。这种量在现实中可能无法真正存在,但在数学上,它提供了一种近乎完美的描述变化的方式。
通过引入无穷小,微积分使得我们能够在变化的过程中捕捉极为微小的差异,进而理解整个系统的动态行为。
比如说你站在海边,看着潮水慢慢上涨。你突然想要精确计算海水每一秒钟的上升高度,传统数学方法可能只会告诉你在某一时刻前后的平均变化。但如果你想知道在某一特定时刻的瞬时变化——即那一瞬间水位的上升速度,传统方法便无能为力了。
瞬时变化率,正是通过将时间间隔缩小到无穷小时得到的结果。
无穷小的思想在微积分中最终落实为极限的概念。通过极限,我们能够分析当变量接近某一特定值时函数的行为,而不必关心该值实际能否被达到。
就像刚刚提到的对于海水上涨的例子,极限的概念帮助我们精确地理解了海水在某一特定时刻的上升速度。虽然我们无法实际观测到一个时间点的变化,但通过极限,我们可以将时间间隔缩小到极致,直到无限接近于零,从而捕捉到瞬时的变化率。
实际上催化微积分的诞生的三个难题第一个就是瞬时速度的计算。
催生微积分的三大难题
微积分的诞生并非偶然,它是为了解决一系列看似简单但实际上极为棘手的问题。这些问题困扰了古代数学家们许久,最终催生了微积分这门强大工具的诞生。这三大难题分别是:瞬时速度的计算、切线斜率的求解以及曲线下面积的求取。

1. 计算瞬时速度
当我们谈论物体的运动时,速度是一个非常重要的概念。然而,在微积分诞生之前,人们只能计算平均速度,即物体在一段时间内的总位移除以这段时间的长度。然而,这并不能满足我们对于瞬时速度的需求。

2. 求切线的斜率
另一个催生微积分的难题是如何求解曲线在某一点的切线斜率。在几何学中,斜率是描述直线倾斜程度的一个重要量。然而,当我们面对曲线时,求解某一点的切线斜率变得复杂起来。传统方法要求至少两个点来计算直线的斜率,但在一条曲线的某一点上,我们只有一个已知点,如何求解与曲线相切的直线的斜率呢?

3. 求曲线下面积
微积分诞生的第三个重大难题是如何求取曲线下面积。对于规则图形,如矩形、圆形,我们可以直接使用几何公式来计算其面积。然而,对于曲线下方的不规则区域,传统几何方法束手无策。

微积分通过引入导数来解决瞬时速度和切线斜率的计算问题。通过将曲线下方的区域分割成无数个极小的矩形并累加它们的面积(积分),解决了求曲线下面积的问题。
极限、导数、积分是构筑微积分理论的核心概念:
- 极限:当变量无限接近某一特定值时,函数的行为或结果。
- 导数:变化率的定量描述。
- 积分:变化量的累积。
极限是导数和积分的基础。通过极限,我们可以探讨函数在某一点附近的行为,而不必关心该点上的具体值。这种方法让我们能够定义导数,即在某一点的变化率,从而捕捉瞬时变化的本质。同样,积分也依赖于极限的概念,通过极限,我们能够累积无数个微小变化,得到总量的精确计算。
从积分法的诞生到牛顿归纳出微积分学竟然经历了 1800 年!
原创 神永正博 图灵新知 2023 年 05 月 31 日 19:00 北京
一文讲透微积分的本质
伟大的发现会成为未来的常识。

01 微积分的本质
“微积分的基本定理” 是微积分的重要内容,其重要性类似于金枪鱼中的珍贵鱼腩部分。高中教科书通常会涉及这方面知识,如 “微分和积分互为逆运算”,该表述正确,但未能充分传达定理的深意。从积分法被发现到牛顿归纳出微积分学,历经约 1800 年,此定理的内涵绝非字面意思那么简单。
人们常感觉圆和球有相似之处,关于圆和球存在以下表述:
- “圆的面积” 的微分就是 “圆的周长”。
- “球的体积” 的微分就是 “球的表面积”。
以数学计算来验证:
- 半径为 r r r 的圆的面积公式为 S ( r ) = π r 2 S (r) = \pi r^{2} S(r)=πr2,对其求微分,根据求导公式 ( X n ) ′ = n X n − 1 (X^n)^\prime = nX^{n - 1} (Xn)′=nXn−1,可得 S ′ ( r ) = 2 π r S^\prime (r) = 2\pi r S′(r)=2πr,这与半径为 r r r 的圆周长公式 C = 2 π r C = 2\pi r C=2πr 完全一致。
- 半径为 r r r 的球的体积公式为 V ( r ) = 4 3 π r 3 V (r) = \frac{4}{3}\pi r^{3} V(r)=34πr3,对其求微分, V ′ ( r ) = 4 π r 2 V^\prime (r) = 4\pi r^{2} V′(r)=4πr2,这正是半径为 r r r 的球的表面积公式 S = 4 π r 2 S = 4\pi r^{2} S=4πr2。
从图形角度进一步理解:
-
对于圆,设半径为 r r r 的圆(圆板)面积是关于 r r r 的函数 S ( r ) = π r 2 S (r) = \pi r^{2} S(r)=πr2。当圆的半径增加 Δ r \Delta r Δr 时,增加的部分是薄圆环。该环状面积大致可表示为 “圆的周长 × Δ r \times \Delta r ×Δr”,即 Δ S ≈ \Delta S \approx ΔS≈ 圆的周长 × Δ r \times \Delta r ×Δr。

由于外侧圆的周长略大于内侧圆的周长,所以使用 “约等于” 符号。为使等式更严谨,两边同时除以 Δ r \Delta r Δr,得到 Δ S Δ r ≈ \frac{\Delta S}{\Delta r} \approx ΔrΔS≈ 圆的周长。
当 Δ r → 0 \Delta r \to 0 Δr→0 时,取 Δ S Δ r \frac{\Delta S}{\Delta r} ΔrΔS 的极限,去掉 “约等于”,即 d S d r = \frac{dS}{dr} = drdS= 圆的周长,所以 “圆的面积” 的微分 = “圆的周长” 成立。
-
对于球,半径为 r r r 的球体积为 V ( r ) = 4 3 π r 3 V (r) = \frac{4}{3}\pi r^{3} V(r)=34πr3。当球的半径增加 Δ r \Delta r Δr 时,体积增加的部分是球外侧很薄的那部分,其体积大致为 “球的表面积 × Δ r \times \Delta r ×Δr”,即 Δ V ≈ \Delta V \approx ΔV≈ 球的表面积 × Δ r \times \Delta r ×Δr。

与圆的处理方法相同,两边除以 Δ r \Delta r Δr,并取 Δ r → 0 \Delta r \to 0 Δr→0 时 Δ V Δ r \frac{\Delta V}{\Delta r} ΔrΔV 的极限,可得 d V d r = \frac{dV}{dr} = drdV= 球的表面积,所以 “球的体积” 的微分 = “球的表面积” 成立。
这一关系实际上就是 “微积分的基本定理”,从不同角度理解:
-
从圆的角度看,“圆面积的微分” 在 Δ r \Delta r Δr 趋向于 0 的极限情况下,可看作把圆分割成薄圆环状,粗略来讲,微分就是从圆板上多个同心圆之间排列的薄圆环中取出 1 个薄圆环;而积分则是累加极薄圆环的面积从而求出圆的面积。

圆环的面积( ≈ L ( r ) Δ r \approx L (r)\Delta r ≈L(r)Δr, L ( r ) L (r) L(r) 为圆的周长),累加所有圆环面积就是圆的面积,即
π r 2 = ∫ 0 r L ( r ) d r = ∫ 0 r 2 π r d r \pi r^{2} = \int_{0}^{r} L (r) dr = \int_{0}^{r} 2\pi r\mathrm{d}r πr2=∫0rL(r)dr=∫0r2πrdr,
两边除以 2 π 2\pi 2π,得出
∫ 0 r r d r = 1 2 r 2 \int_{0}^{r} r\mathrm{d}r = \frac{1}{2} r^{2} ∫0rrdr=21r2。
-
从球的角度看,累加 “表面积 × Δ r \times \Delta r ×Δr” 就能求出球整体的体积,即
∫ 0 r 4 π r 2 d r = 4 3 π r 3 \int_{0}^{r} 4\pi r^{2} \mathrm{d}r = \frac{4}{3}\pi r^{3} ∫0r4πr2dr=34πr3,
两边除以 4 π 4\pi 4π,得
出 ∫ 0 r r 2 d r = 1 3 r 3 \int_{0}^{r} r^{2} dr = \frac{1}{3} r^{3} ∫0rr2dr=31r3。
将微分公式 ( r 2 ) ′ = 2 r (r^{2})^\prime = 2r (r2)′=2r, ( r 3 ) ′ = 3 r 2 (r^{3})^\prime = 3r^{2} (r3)′=3r2 代入,也可得到相应的积分公式。
由此可知,“分割” 成较小部分的操作是微分,“累加” 较小部分的操作是积分。

微分和积分如同硬币的正反面,是完全相反的关系。
02 基本定理的使用方法
理解 “微积分的基本定理” 后,会发现其并不复杂,且应用范围广泛,实用性强。
幂函数
以 “幂函数的微分公式” ( x α ) ′ = α x α − 1 (x^{\alpha})^\prime = \alpha x^{\alpha - 1} (xα)′=αxα−1 为例推导 “幂函数的积分公式”。

根据微积分的基本定理,幂函数的微分公式表示 α x α − 1 \alpha x^{\alpha - 1} αxα−1 的积分是 x α x^{\alpha} xα。
改变 α \alpha α 的值,可列举出:
3 x 2 3x^{2} 3x2 的积分是 x 3 x^{3} x3, 4 x 3 4x^{3} 4x3 的积分是 x 4 x^{4} x4 等。
将这些式子分别除以相应系数,可得 x 2 x^{2} x2 的积分是 1 3 x 3 \frac{1}{3} x^{3} 31x3, x 3 x^{3} x3 的积分是 1 4 x 4 \frac{1}{4} x^{4} 41x4。一般来说, x β x^{\beta} xβ 的积分是 1 β + 1 x β + 1 \frac{1}{\beta + 1} x^{\beta + 1} β+11xβ+1。
但在使用 “积分” 概念时需注意,对于幂函数, 1 β + 1 x β + 1 \frac{1}{\beta + 1} x^{\beta + 1} β+11xβ+1 的微分是 x β x^{\beta} xβ,然而存在其他函数,其微分结果同样为 x β x^{\beta} xβ,这是因为遗漏了微分得 0 的函数,即 “常数函数”。常数函数的斜率为 0,对于任意 x x x 值,函数结果相同,设常数函数值为 C C C,可表示为 y = f ( x ) = C y = f (x) = C y=f(x)=C。

综上, x β x^{\beta} xβ 的积分是 1 β + 1 x β + 1 + C \frac{1}{\beta + 1} x^{\beta + 1} + C β+11xβ+1+C,用符号表示为 ∫ x β d x = 1 β + 1 x β + 1 + C , \int x^{\beta} \mathrm{d}x = \frac{1}{\beta + 1} x^{\beta + 1} + C, ∫xβdx=β+11xβ+1+C,这就是幂函数的积分公式。
对 f ( x ) f (x) f(x) 的微分进行积分得出的函数,称为 “ f ( x ) f (x) f(x) 的原函数”,记为 F ( x ) F (x) F(x),即 ∫ f ( x ) d x = F ( x ) + C \int f (x) \mathrm{d}x = F (x) + C ∫f(x)dx=F(x)+C
不定积分 / 定积分
原函数中存在 “一项不定数值 C C C(不定项)”,这种 “通过积分求出原函数” 的积分称为不定积分;而求取面积或体积的积分,称为定积分。不定积分原则上不写积分区间,而定积分需要明确积分区间。
在计算面积等问题时,常数 C C C 会在计算过程中消除。例如,计算函数 f ( x ) f (x) f(x) 在区间 [ a , b ] [a,b] [a,b] 上与 x x x 轴围成的灰色部分面积,用定积分符号表示为 ∫ a b f ( x ) d x , \int_{a}^{b} f (x) \mathrm{d}x, ∫abf(x)dx, 其定积分的值为
∫
a
b
f
(
x
)
d
x
=
[
x
=
b
时不定积分的值
]
−
[
x
=
a
时不定积分的值
]
\int_{a}^{b} f (x) \mathrm{d}x = [x = b\; 时不定积分的值 ] - [x = a\;时不定积分的值]
∫abf(x)dx=[x=b时不定积分的值]−[x=a时不定积分的值]

因此,正如我们所知,
f
(
x
)
=
x
β
f (x) = x^{\beta}
f(x)=xβ 的不定积分是
1
β
+
1
x
β
+
1
+
C
\frac{1}{\beta + 1} x^{\beta + 1} + C
β+11xβ+1+C
计算其面积为
∫ a b x β d x = ( 1 β + 1 b β + 1 + C ) − ( 1 β + 1 a β + 1 + C ) = 1 β + 1 b β + 1 − 1 β + 1 a β + 1 \begin{align*} \int_{a}^{b}{{{x}^{\beta }}}dx & =\left( \frac{1}{\beta +1}{{b}^{\beta +1}}+C \right)-\left( \frac{1}{\beta +1}{{a}^{\beta +1}}+C \right) \\ & =\frac{1}{\beta +1}{{b}^{\beta +1}}-\frac{1}{\beta +1}{{a}^{\beta +1}} \end{align*} ∫abxβdx=(β+11bβ+1+C)−(β+11aβ+1+C)=β+11bβ+1−β+11aβ+1
这样, C C C 通过相减就消除了。
以具体例子说明:
- 对于向右上方倾斜
4
5
∘
45^{\circ}
45∘ 的直线
y
=
x
y = x
y=x,计算从
x
=
1
x = 1
x=1 到
x
=
2
x = 2
x=2 之间的面积。

- 用梯形面积公式计算:该梯形上底为 x = 1 x = 1 x=1 时 y y y 的值,即 y = 1 y = 1 y=1;下底为 x = 2 x = 2 x=2 时 y y y 的值,即 y = 2 y = 2 y=2;高为 2 − 1 = 1 2 - 1 = 1 2−1=1,根据梯形面积公式 ( ( ( 上底 + + + 下底 ) × ) \times )× 高 ÷ 2 \div 2 ÷2,可得面积为 ( 1 + 2 ) × 1 ÷ 2 = 3 2 (1 + 2) \times 1 \div 2 = \frac{3}{2} (1+2)×1÷2=23。
- 用积分公式计算: ∫ 1 2 x 1 d x = 1 1 + 1 2 1 + 1 − 1 1 + 1 1 1 + 1 = 3 2 , \int_{1}^{2} x^{1} \mathrm{d}x = \frac{1}{1 + 1} 2^{1 + 1} - \frac{1}{1 + 1} 1^{1 + 1} = \frac{3}{2}, ∫12x1dx=1+1121+1−1+1111+1=23, 与梯形面积公式计算结果一致。
- 对于抛物线 y = x 2 y = x^{2} y=x2,计算从 x = 1 x = 1 x=1 到 x = 2 x = 2 x=2 的面积。由于无法使用梯形面积公式,只能用积分计算, ∫ 1 2 x 2 d x = 1 2 + 1 2 2 + 1 − 1 2 + 1 1 2 + 1 = 7 3 , \int_{1}^{2} x^{2} dx = \frac{1}{2 + 1} 2^{2 + 1} - \frac{1}{2 + 1} 1^{2 + 1} = \frac{7}{3}, ∫12x2dx=2+1122+1−2+1112+1=37,一瞬间就可以得出答案。
前文提到的圆的面积 ∫ 0 r r d r = 1 2 r 2 , \int_{0}^{r} rdr = \frac{1}{2} r^{2}, ∫0rrdr=21r2, 球的表面积 ∫ 0 r r 2 d r = 1 3 r 3 , \int_{0}^{r} r^{2} dr = \frac{1}{3} r^{3}, ∫0rr2dr=31r3,相关公式只是把 x x x 换成了 r r r,是幂函数积分公式在 β = 1 \beta = 1 β=1、 β = 2 \beta = 2 β=2 时的特殊情况。
03 微积分的本质:近似与忽略
微积分的精髓:在于通过近似和忽略,将复杂问题简化为易于处理的模块化形式。
近似的意义:近似并非追求绝对精确,而是允许我们忽略部分细节,以获得问题的整体解或近似解。 这种策略在处理复杂系统时尤为重要。
微积分的典型应用:
- 积分: 将复杂形状视为无限多个简单几何图形(如矩形)的组合,从而计算其面积、体积等。
- 微分:将函数在局部范围内近似为直线(切线)或抛物线,从而研究函数的局部变化率(导数)。
忽略的重要性:
- 微积分强调忽略次要细节,着眼于问题的关键特征。
- 通过“用直线段近似函数图像”等方法,可以解决诸如最优化问题(例如冰淇淋蛋卷筒的最大容积)和曲线长度计算(例如悬链线的长度)等难题。
- 将复杂问题分解为多个小而简单的子问题,然后通过累加这些子问题的解来获得整体解,是微积分解决复杂问题的核心策略。
数学的普适性: 近似与忽略的思想不仅限于微积分,而是贯穿整个数学体系。 微积分是理解和掌握这种思想的绝佳载体。
现实世界的近似:
- 现实世界中,极限概念(如无限小、无限大)并不存在。 例如,存在最小的不可再分的基本粒子,宇宙的大小也是有限的。
- 微积分中引入无限小和无限大的概念,是一种理想化的近似,旨在简化计算和分析。
微积分的价值:
-
虽然微积分的某些假设(如忽略基本粒子的大小、忽略宇宙的边界)可能与物理现实不符,但这种近似方法极大地简化了复杂问题的求解,并为我们提供了强大的分析工具。
-
通过学习微积分中的各种概念(如图形分割、自然常数 e e e、悬链线等),逐步培养“近似与忽略”的思考方式。 掌握这种思考方式是理解微积分乃至整个数学体系的关键一步。
在无限与变化之间:一场关于微积分的深度对话
原创 Ramakrishna 返朴 2025 年 05 月 09 日 07:59 北京
美国康奈尔大学教授史蒂文・斯托加茨(Steven Strogatz)因在动力系统 [1] 与复杂网络理论 [2] 领域的开创性贡献享誉数学界。在动力系统领域,他研究了蟋蟀的同步鸣叫等现象;在复杂网络理论方面,他于 1998 年在《自然》杂志发表的论文《小世界网络的集体动力学》(Collective dynamics of small-world networks)[3] 掀起了一场持续至今的研究热潮。尽管取得了诸多成就,斯托加茨或许会说,他最重要的身份并非研究者,而是 “翻译者”。
在一次与 The Believer 杂志的访谈对话中,从斯托加茨教授的著作《微积分的力量》谈起,教授通过微积分历史上的最重要人物阐述了数学与自然的关系,并对确定性和不可预测性进行了分析。
采访 & 写作 | Prashanth Ramakrishna
翻译 | Alex
在搜寻混沌理论课程的补充材料时,我第一次接触到斯托加茨博士的工作。他的著作 Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering 对于我深入理解数学具有重要意义 —— 我当时对数学的定义还停留在封闭课堂环境中的定理、证明和计算。但实际上,数学的力量在于它能够极其精确地描述自然世界的运行规律,并利用这些描述预测未来的发展变化。不久之后,我开始从事涉及现实世界动态现象建模的工作,比如研究青春期大鼠看似随机的睡眠 - 觉醒周期、动脉中血液脉搏波的反射,以及组织如何通过招聘来维持意识形态的多样性。事实上,斯托加茨的启发彻底改变了我对数学的看法,我意识到,如同画家挥动画笔,数学家运用数学描绘出了现实世界的某种面貌。万物皆模式(Life is patterns),关键在于能否有人将它们辨识出来。这种顿悟,我确信,不会只发生在我一个人身上。

Steven Strogatz(照片由 John Groo 提供)
在一个以严寒著称的伊萨卡市的冬日,我满怀期待地来到康奈尔大学 —— 这里正是斯托加茨博士任教的地方,他担任 Jacob Gould Schurman 应用数学教授。我这次专程为他的新书《微积分的力量》(Infinite Powers: How Calculus Reveals the Secrets of the Universe,2019)而来。我们在他的办公室里聊了好几个小时 —— 不仅谈到了微积分的历史,也聊到了父亲在我小时候与我玩的一些(数学)近似游戏、人文与科学之间的分歧、良好的数学教育应具备哪些要素、数学模型的局限,以及美感、直觉与创造力在数学中的重要作用等诸多话题。本文即是那场对话的编辑整理版。
采访结束后,斯托加茨教授非常友善地开车送我回到了我当时居住的那间略显破旧的兄弟会宿舍。当天深夜,在烟草和披萨的混合香气中,我与一个学生闲聊起来。当我提到斯托加茨教授时,他一下子兴奋起来:“动力学传奇啊!Watts-Strogatz 模型,不就是他吗?大家都说一定要上他的课!可惜课程安排不允许,实在遗憾。”
01 微积分的天体起源
The Believer(以下简称 BLVR):在我看来,《微积分的力量》不仅试图解释微积分是如何发展的,还试图说明它为何行之有效。这种理解是否过于简单?是否符合你写作这本书的初衷?
斯托加茨(以下简称 SS):我写这本书主要想探讨三件事。前两件相互关联 —— 正如你所说,我想解释微积分的由来以及它为何有效。第三件事是展示微积分如何改变人类的生活。我的目标是要将历史、概念和应用全部融入到书中。不过,历史并非我的专长。数学史上流传着许多轶事趣闻,想想你的老师们,他们很可能也讲过高斯或黎曼的故事。我发现,几个世纪以来,我们一直喜欢谈论这些话题。我甚至觉得自己了解阿基米德是什么样的人。当然,这不过是自欺欺人罢了。
BLVR:人们往往倾向于神化数学家,仿佛他们拥有超能力一般。数学家的殿堂里汇聚了如此多样的人物。但我总觉得这种多样性呈现出一种两极分化的状态,一端是极度自负,另一端则是全然忘我。这种二元性在书中的一些人物身上得到了很好地体现。
SS:是的,像是费马和笛卡尔,还有牛顿和莱布尼茨。关于伽利略和开普勒,虽然我不会将他们称为对手,但他们是同时代的人,可以很自然地并列提及。然而,我最终还是省略了许多重要的历史人物,比如黎曼、高斯、柯西和拉格朗日。写书时我开始意识到,我希望能尽量降低这本书的数学门槛。比如,我甚至要假设我的编辑没学过高中代数。如果连这些基础都没有,那谈论黎曼的成就又有什么意义呢?我希望真实地呈现数学,这样任何读者都能从零开始理解。
BLVR:幸运的是,要讨论微积分的两个主要组成部分 —— 微分和积分,并不需要复杂的历史背景。说到这里,我意识到人们往往会忽略数学名词本身所包含的解释价值:“微分” 是将连续的整体分解成无限小的组成部分;而 “积分” 则是将许多细小的部分重新整合为一个整体。
SS:我也这样认为。你这种说法似乎特别自然。微积分之所以十分强大,是因为世界上许多事物都可以被视为连续体,并且可以不断细分。时间、空间及物质实体,皆是如此。
BLVR:问题是:为什么微积分会产生如此深远的影响?
SS:如果要用一句话总结,那就是:微积分是研究 “变化” 的数学。更准确地说,它研究的是 “连续变化”。我们这里说的不是那种胡搅蛮缠的变化,而是比如一位 HIV 感染者在接受三联鸡尾酒疗法后,血液中的病毒载量会迅速下降这样的变化;也包括太阳系天体是如何运动的,这曾是早期重要的未解之谜,并由此引出了一个有趣的问题。纵观历史,人类如此痴迷于星辰、月亮和太阳,但是,为什么?为什么这些天体是人类最早能够数学化的对象?那时候,人们对草药、动物和农业已经有所了解,但在这些领域,基本只依靠计数就足够了。为什么那些高深的数学(比如三角函数的微积分运算)最先应用在天文学上?我心里有个答案,不过我很好奇你有没有想过这个问题。
BLVR:是的,我也想过这个问题。我认为这个问题的答案有两部分。第一,某些天体的运行显然有规律可循,即使人们一开始不清楚这些规律具体是什么,也能强烈地感知到它们的存在,而且只要仔细观察,假以时日就能发现。第二,那些规律能够被可靠地观测到。而这两点,最终成为科学的必要前提:察觉到某事物值得研究并找到研究它的可靠方法。
SS:非常好。另外,天体运动的时间尺度也刚刚好 —— 既不太快,也不太慢。那些变化非常迅速的现象,甚至只是从桥上扔下一块石头,在当时其实是很难研究的,因为那时没有足够精确的时钟,无法测量石头落入水中的时间。一切都发生得太快了!另外也要记住,这些观测工作往往是在夜晚进行的,没有电灯,四周漆黑一片。而在世界上很多地方,夜空本身就非常壮观。
不过,同样让人费解的是,这些天体距离地球非常遥远,人类为什么会想要研究它们?你可能会认为理应最先发展医学,因为它关乎生死,是人类最迫切需要解决的问题。但医学太复杂了,直到今天,其中的规律仍然成谜。所以,我想你说得对 —— 天体运动呈规律性,运行速度缓慢,而且肉眼可以观测到。因此,人们可以绘制图表并记录下来。最终,最遥远的对象反而最先被理解。微积分正是在那场追寻行星运动规律的古老探索中逐渐萌芽的。而 “行星” 一词的本意,正是 “漫游的星辰”。
BLVR:仰望星空是一种分离 “运动现象” 的自然方式。许多最早为微积分奠定基础的重要进展都源于 “人为分离运动现象” 方法的发展。比如,我现在脑海中浮现的就是伽利略让小球在带槽斜面上滚动的实验。正是这种方法论上的突破,我们才能研究地球运动规律。
SS:是的,伽利略的实验继承了阿基米德的精神。阿基米德做了很多漂浮物体和类似性质的简化实验。伽利略就像是现代版的阿基米德。方法论的另一个重大突破就是刻意忽略某些因素的影响。比如,摩擦力在现实生活中不可或缺,而伽利略却费尽心思将小球轨道打磨得光滑笔直,因为他对摩擦力不感兴趣。他真正想理解的是重力以及重力如何影响物体的运动。
做这些小实验是为了弄清楚宇宙中的事物是如何变化的,而描述这种变化的语言就是微积分。在代数中,我们会学到用关系式来思考问题,比如 “距离 = 速度 × 时间”。但这只适用于物体匀速运动的时候,而宇宙中很多物体并非匀速运动,比如行星围绕太阳旋转,靠近太阳时速度加快,远离时就慢下来。再比如,迈克尔・乔丹扣篮时,跳到最高点时好像悬停在空中,接着突然加速下落。这些运动的速度变化必须找到方法描述。而几何也有类似的局限:古典几何学能够处理直线构成的形状,并用直线几何方法来量化光滑曲线(如抛物线)下的面积。但要处理光滑曲线,需要一种新的思想,那就是微积分。
02 邻近于美
BLVR:微积分的发展凝聚了众多数学家的智慧。因此,我想我们是不是应该介绍一下你书中的重要人物?
SS:我本想在书中讲述一千个人物的故事,但碍于篇幅所限,我决定重点介绍阿基米德。我认为他是古代最重要的数学家,他当时所解决的问题,现在仍然困扰着 SAT 的考生。阿基米德成功量化了许多由光滑曲线构成的形状,比如圆、球体和抛物线。微积分的核心就是 “变化”。直线的方向不会发生改变,而根据定义,曲线的方向则不断变化。因此,曲线是研究 “变化” 的重要内容。阿基米德是第一个能够通过测量曲面物体的属性(如表面积、体积和弧长)描述这种变化的人,而这一切的背后,是他对 “无穷” 的驾驭。
BLVR:他驾驭无穷的方法,便是巧妙地将物体拆解再重新组合,从而为后来微积分的发展提供了重要线索。
SS:他简直是切割形状的艺术大师。这很像立体主义。布拉克(Georges Braque,法国著名立体主义画家)有一幅画作,用万花筒一样的视角展现人走下楼梯的场景。从不连续的画面中,你却能感受到连续的动作。如何将锯齿状的碎片变成光滑的形状呢?立体主义画家在 20 世纪初懂得了这个方法,而阿基米德早在公元前 250 年就知道怎么做了:他将一个像抛物线般平滑的形状,分解为许多越来越小的三角碎片。多么奇妙的画作!
阿基米德至今仍然如此重要,真是不可思议。动画人物史莱克光滑的肚子或喇叭形的小耳朵都是由数百万个多边形构成的。所有的计算机图形都巧妙地利用无数个微小的多边形来近似平滑的面部、腹部、耳朵和其他所有部位。面部外科医生使用相同的技术来预测整形手术的结果。因此,通过运用阿基米德的思想,我们可以为外科医生提供真正有效的 “手术模拟”。
BLVR:那古典时代之后呢?
SS:我们直接跳到两千年后的 17 世纪初,那时人们开始量化地球上和天空中物体的运动方式。接下来登场的是伽利略和开普勒。他们既是数学家,也都是富有科学精神、目光投向数学之外的探索者。他们研究数学的目的并非仅为数学本身,同时也怀抱着对自然的敬畏之情。
开普勒是个虔诚的信徒。尽管他最后当了老师,但年轻的时候他本打算做一名路德教的牧师。他曾一度形容自己处于一种 “神圣狂热” 的状态。他对宇宙的规律抱有一种神秘主义的看法,认为自己正在发现上帝用来创造宇宙的神圣几何。开普勒发现了行星运行所遵循的定律。虽然他当时还不知道万有引力定律,但他在行星运行中发现了大量的几何结构。在开普勒之前,哥白尼就提出行星围绕太阳运行的设想,但开普勒用数学方法证明了这一点。
BLVR:你对开普勒的描述,我很感兴趣,因为从毕达哥拉斯开始,数学神秘主义就是另一条重要的历史脉络。
SS:我们不妨说明一下什么是数学神秘主义。开普勒就是一个神秘主义者,让我们以他为例。当时,除了地球之外,还有五颗已知的行星,它们靠近太阳,分别是水星、金星、火星、木星和土星。有趣的是,如果你画一个五角星,并连接它的五个角,就会得到一个五边形。另一种更传统的思考方式是:如果你画一个五边形,然后从内部连接它的角,那么你不仅会得到一个五角星,还会在原始图形中心生成一个小五边形。五边形是一种能够自我生成的形状,并且可以无限延续下去。因此,根据丹・布朗(Dan Brown,美国悬疑小说作家)的说法和毕达哥拉斯的观点,五边形象征着生育和女性。“5” 在毕达哥拉斯的数字命理学中非常重要,而开普勒深受其影响。他注意到有五颗行星,同时也发现五种特殊的立体图形,即柏拉图立体(立方体或正四面体),它们的每个面都是相同的正多边形。于是他心想:“它们之间一定有联系!” 开普勒得出结论,宇宙是基于柏拉图几何构建的。他在著作《宇宙的奥秘》(MysteriumCosmigraphicum)中提出了一个方案:立方体内嵌套着十二面体 [4],十二面体内又嵌套二十面体 [5],几乎可以解释五颗行星的位置以及它们与太阳之间的平均距离。这是一个美丽的设想,可惜大自然并没有采用。
数学是宇宙的秘密吗?开普勒对此深信不疑,毕达哥拉斯学派亦是如此 —— 据说毕达哥拉斯在发现音乐的和谐遵循数学定律后说出了那句 “万物皆数”。这是一个贯穿整个数学发展历程的主题。如今我们已很少谈论这个话题,因为我们不想把自己视为神秘主义者。但它依然存在。人们认为某些理论之所以优美(比如超对称就是量子理论极为优雅的概括),或许是因为这种美感本身就蕴含着某种启示。这种启示无疑对爱因斯坦最有效:最美的相对论版本最终被证明是最好的。数学之美与真理之间存在着复杂的关系。美能指引我们发现真理吗?遗憾的是,并非总能如愿。但有时可以。
BLVR:在纯数学领域,人们往往强调优雅(elegance),而优雅或多或少等同于简洁(simplicity)。只要人们继续把美和简洁联系在一起,并始终渴望简洁能够对应事物的根本,那么我认为美依然会是探寻真理的指路明灯。审美意识在数学直觉中占据重要地位,或许我们需要些许抛弃已有的认知才能习得。
SS:让我们再来说说开普勒。与前人一样,开普勒认为行星的运行轨迹应该是一个圆,因为圆形是最简单、最完美的形状。时至今日,人们仍然将圆形视为完美和永恒的象征。我们选择圆形作为结婚戒指并非偶然 ——“我爱你直到永远” 正如 “圆永无止境”。然而,当我们真正观察行星的运动时,会发现它们并非严格地沿着圆形轨道运行。但另一方面,它们的轨道又非常接近圆形。因此,开普勒像托勒密和其他先贤一样,试图找到一种方法解释这一点 —— 这在古代天文学中被称为 “拯救表象”(saving the appearances)。
BLVR:真理就是近似于美。
SS:最后证明,行星运行轨道并不是圆形,而是椭圆。它与圆形非常相似。想象一下,你以一个圆形为底,像饮水机旁的纸杯那样不断扩展,就能形成一个圆锥。然后你以一个倾斜的角度切割纸杯,得到的截面便是椭圆形。可见,圆锥从圆形而来,而椭圆则来自切割圆锥。这个纯几何学中的简单形状竟然揭示了行星围绕太阳的运行轨迹 —— 这就是著名的开普勒第一定律。观测数据与理论完美契合,开普勒是对的!他认为上帝会运用几何学的偏见似乎得到了印证。而且,这个答案如此简单。
另一个同样简单的 “真理” 是伽利略的发现:物体在空中抛掷后的轨迹呈抛物线形状。“道义上” 来说 [6],篮球的投篮轨迹也呈抛物线状。然而,由于恼人的空气阻力,实际情况并非如此。因此,现实世界…… 总是近似于美。这也引出一个问题:我们应该关注真实发生的现象,还是沉浸在柏拉图式的理想世界中,探究事物 “本应如此” 的状态?如果盲目地追求真理,反而可能无法洞察那些隐藏在些许 “谎言” 下的更深层原理。完美的抛物线弧线就是一种 “谎言”。伽利略常常选择这种 “谎言”;他选择看到事物的理想状态。
这与艺术有很多共通之处。我非常喜欢毕加索的一句名言:“艺术是一种谎言,教我们理解真理。” 我觉得很多伟大的科学家心中都有这种冲动。为了探寻更深层次的真理,他们会忽略一些不便利的因素。然而,这种做法也存在巨大的风险,因为有可能会被认为是不诚实(intellectually dishonest)。
BLVR:两千年来,人们不断探索各种问题的解决方法,而这些方法都隐约暗示着微积分之类的数学应该被形式化。随后,牛顿横空出世,他准备融汇前人的思想,成为那位伟大的集大成者。
SS:关于牛顿,实际上还有一些不太清楚的地方。我们应该视他为划时代的革命者,还是 “站在巨人的肩膀上” 的集大成者?事实上,两者皆是。最初了解他时,我曾认为人们对他的评价过高,但随着研究的深入,我逐渐认识到,牛顿确实应当与历史上那些最伟大的人物齐名 —— 但更多是因为他运用数学深刻影响了我们思考其他学科的方式,尤其是物理学和天文学。牛顿让我们看到:自然是有逻辑的。而在他之前,我们对此一无所知。但人们通常不这样表述,大多数人会说:“他发现了运动定律。” 牛顿为当时已知的所有地球和天体运动提供了一致的解释,即其著作《自然哲学的数学原理》第三卷中所提出的 “世界体系”(The System of the World),其中还包括潮汐、彗星等传统上不被提及的自然现象。人们常说 “他发明了微积分”,但这种说法并不准确。牛顿的确将所有前人已知的知识系统地整合起来,形成一个成体系的系统,一套如今已高度精简和完善的算法,甚至可以教授给普通高中生。或许牛顿成就最有力的证明就是:他将微积分变得非常机械化,人们甚至不需要理解就能进行运算。遗憾的是,这恰恰是许多学生学习微积分的常态。
03 拉普拉斯妖和心智景观
BLVR:微积分的应用显然极其广泛。但正如你在书中提到的,它也存在一定的局限性。更确切地说,微积分在预测时所依赖的决定论并非总能成立。你使用了一个源自拉普拉斯**[7]的思想实验说明这一点,你能否展开谈谈,为什么 “拉普拉斯妖”(Laplace’s Demon)掌控的 “机械宇宙”(Clockwork Universe)[8]**无法成立?为什么它的不成立意味着决定论乃至微积分的局限性?
SS:在 20 世纪 70 至 80 年代混沌理论兴起之前,曾有这样一种普遍看法:如果一个系统是决定性的(也就是说,其运行规则中丝毫不含偶然或随机的成分),那么它就像一部电影,只要被重放,情节总会分毫不差地重演一遍。人们相信,任何遵循决定论的系统都是可预测的…… 至少在理论上是这样。因此,只要你能准确测量宇宙中所有粒子初始时的位置和运动速度,牛顿定律就能推断出它们此后每时每刻的运动轨迹。所谓的 “拉普拉斯妖”,便是这样一个拥有无穷智慧的假想生灵,它能洞悉每一个粒子的确切位置与速度,并据此计算出整个宇宙的未来 —— 从历史进程到我们每一个人的情感波动,包罗万象。
拉普拉斯妖主宰着一个遵循牛顿定律的决定论机械宇宙,这种思想实验展现的图景本身就令人不安。出于种种原因,如今我们已不再相信这种设想了。现代观点认为,“量子力学已取代牛顿定律,成为物理学的主要定律。” 然而,即便是在一个完全遵循经典牛顿定律的宇宙中,人们也无法对任意遥远的未来做出预测。你只能将测量结果精确到一定的位数。传统上,人们认为,只要测量得足够精确,就能预测出超越宇宙年龄的未来。因此,在实践中,人们应该能通过不断提高初始条件的测量精度来改善预测的准确性。然而,实际情况并非如此,尤其是在 20 世纪 70 年代混沌理论问世之后。我们了解到,即使是这些简单的力学系统,初始条件测量中的微小误差也会呈指数级增长,导致短时间内预测结果严重偏离实际,我们称这种现象为 “混沌”(Chaos)。这就是难以提前多日预测天气的原因,而理论上,人类根本无法预测数周后的天气。
BLVR:这里有一个关于数学形式主义的问题,最近我常常拿这个问题 “伏击” 朋友,给我带来了不少乐趣。我的问题是:在心智景观(Mindscape)中是否存在一个隐秘角落,其中命题 “P” 与 “非 P” 可以同时为真?
SS:我明白了 —— 也就是说,我们谈论的是一个不遵循 “排中律”(Excluded middle)**[9]**的宇宙。
BLVR:对,这正是我朋友当时的看法,也是我期待你能提到的。心智景观就是由各种思想构成的抽象宇宙。思想相同的两个人可能会在心智景观中占据同一个位置,就像物理世界里两个人可以身处同一个地方。所以,任何你能构想出的事物都存在于心智景观。关于数学有一个不为人知的小秘密:人们可以随意构建任何想要的系统,而这个系统并非一定要对应真实世界。
SS:这是不是说没什么规则可循?我原本以为,数学拥有一套明确的规则。我们必须就具体的逻辑规则达成共识,同时受限于这些规则。
BLVR:至于这种数学系统所描述的某个宇宙是否存在,那就是另一个问题了,对吧?
SS:是的,确实是不同的问题。一个问题是,我们想象出来的数学 “乐园” 是否对应真实世界。但还有另一个更一般的问题,听起来似乎是你想问的:“我们能否有其他类型的数学?甚至其他类型的逻辑?” 这时先不要管真实世界如何。
BLVR:你提到 “真实”(real)一词很有意思。刚才那个问题背后还有一个更深层的问题:数学定律是真实存在的吗?还是说,它们之所以真实,仅仅是因为它们所描述的对象(也就是真实世界)是真实的?那么,数学对象呢?那些理想、完美的对象,它们也是真实存在的吗?
SS:很难用 “真实” 这个词来形容它们。这里还涉及不同世界的问题。罗杰・彭罗斯在其著作《通往实在之路》(The Road to Reality)中提到,存在三个世界:数学世界、心智中的思想世界,以及物理对象构成的 “真实” 世界。我不太习惯这种三分法。通常我认为只有两个世界:柏拉图的理念世界和物质世界。不过,很有意思的一点是,彭罗斯将心智产生的思想和数学概念区分开来。我的理解是,他认为数学概念独立于人的心智存在,但又不像 π 那样存在于 “真实” 世界;π 是一个真实的…… 说实话,我也不太理解他的意思。但某种程度上,我又能理解彭罗斯。作为数学家,当我们发现一个公式,或者揭示出某些数学对象之间的关系时,那种感觉就像是发现了已经存在的事物。这与肖邦创作《夜曲》不同,我不知道肖邦本人会不会这样想:“那些《夜曲》早就在那里了,是我发现了它们。” 虽然米开朗基罗也曾说过,他只是 “把雕像从石头中释放出来”,但它们确实是被创造出来的。那么,微积分基本定理是否曾等着我们去发现?圆周率的概念呢?圆的面积公式呢?给我们的感觉是,它们好像本来就在那里。但问题是 —— 在哪里?
BLVR:探讨数学概念是否是物理实在的自然体现,还有一个论点是基于它们的预测能力。比如,宇宙中有些现象确实表现出类似 e 的规律。我们在数学上把 e 定义为当 n 趋于无穷大时,(1+1/n) n 的极限。你把细菌放进培养皿,它们也会以指数方式增长;与此同时,你可以构造出一个像 e 一样无限不循环的数字,但它与真实世界毫无关系。换句话说,宇宙似乎 “并不知道” 这个假想数字。但不知何故,宇宙似乎 “知道” e。
SS:这其实是我整本书想传达的观点。很多人不喜欢费曼的那句名言:“你必须学微积分,因为微积分是上帝的语言。” 但他这么说并非没有道理。我们现在了解宇宙万象,最好的工具就是微积分。无论是水流的运动、空气的流动、热量的传导、电磁现象还是量子力学,本质上都要靠微积分来描述。如果要让人们说出费曼那样的话,很多人可能会说 “数学是宇宙的语言”。但更准确地说,微分方程才是宇宙的语言。宇宙的 “语言” 并不是那些抽象的代数拓扑,而是由微积分里的各种符号(使用微分算子和积分算子)书写。从原子到星系,所有我们研究过的领域,背后都有微积分的影子。有些熟悉量子力学的人可能会提到最深层的 “路径积分”,但说到底,它也是一种 “积分”,所以它还是微积分!
BLVR:关于 “数学对象到底是不是真实存在” 的问题,其实还可以扩展到那些理想化的模型上。只有将微积分工具巧妙地应用到某些实际模型中,才真正体现出它们的价值。我想我们可以围绕你以前研究过的一个模型来聊聊 —— 我在阅读你的作品时对它产生了兴趣。不过,在这之前我有个问题想问你:为什么人们应该对模型持怀疑态度?
SS:你不妨先描述一下这个模型,看起来你对它还记忆犹新。
BLVR:这个问题是:能否在一个社会中鼓励政治温和的立场?为探究这一问题,你构建了一个极其简化的模型,将一个匿名社群划分为四组群体:其中一组持主流世界观 B;两组持反叛世界观 A—— 其中一组由 “狂热分子” 构成(指其成员固守己见、绝不改变立场);最后一组是温和派,其观点融合了 A 与 B,因此以 AB 表示。你通过一系列微分方程,来描述这些群体的规模如何随时间发生变化。
**SS:**我和合作者是这样设想的:持不同观点的人相遇后,其中一方说服另一方 “改变立场”,并可能在一定概率下成功。我们没有探讨任何细节,如你所说,这是一个高度简化的模型。
BLVR:结果相当悲观。你们尝试从多个角度调整模型,希望长期鼓励温和立场,却几乎没有任何效果。唯一有效的方法是引入一种独立于人际互动之外的外部调节力量。
SS:这股外部力量可以是来自权威机构自上而下的干预,也可能是某种共同经历的外部事件,比如你在节目外提到的 “9・11 事件”。人类文明伊始,统治者们就明白,塑造一个共同的敌人是最有效的社会凝聚手段。《1984》中的大洋国**[10]**不正是长期处于战争状态吗?不过,整个讨论的关键是:数学模型对于任何重要事物是否可靠。将微积分应用到人类事务中其实非常棘手,因为我们没有像描述物理世界的牛顿定律或电磁现象的麦克斯韦方程组那样能够准确描述人类行为的法则。无论在个体层面还是群体层面,我们都无法预测人类的行为,而它在理论上是否可行是真正的哲学问题。我们现在不过是在 “玩游戏”。
从另一个角度看,这类 “游戏” 之所以有趣,是因为它们让我们意识到人类知识的局限性,从而保持一种谦逊的态度 —— 我们对人类行为或社会到底了解多少?这些模型本身常常会展现出令人意想不到的行为特征,比如在那个关于 “温和派” 的小模型中,我们发现,让温和派变得更加顽固,非但没有促进温和,反而更容易让狂热分子占据主导地位。这给了我们一个深刻的教训:你以为自己能知道事态发展,但即使在这样一个刻意简化的 “宇宙” 里,也很难做出准确预测。经验告诉我们,当我们声称某种社会干预会产生这样或那样的效果时,往往并不准确。但这么说好像是虚无主义,太悲观、太消极了。你总是要做些事情,对吧?或者…… 我也不知道该怎么说。
BLVR:我们希望在理论上能够准确预测。但拉普拉斯妖的例子已经告诉我们,这并不现实。我们可以做到某种程度的预测,比如天气预报。实际上对于社会进步这样复杂的事物,我们的预测能力也可能只在某个特定界限内有效。我们越接近那个界限,就越能做出正确的决策。但界限始终存在,而人类事务又太复杂、太混乱,所以我们也许永远都无法做出最好决策,甚至连稍好的决策都难以实现。这种无力感,确实让人沮丧。
SS:行为经济学中有一些看似简单却行之有效的原则。以目前美国器官捐赠为例,如果你在车祸中不幸身亡,你需要在生前明确表示愿意捐献器官,并进行登记,才会成为器官捐献者。默认情况下,你不是器官捐献者,但并非必须如此。理查德・塞勒(Richard Thaler)**[11]**提出了 “助推”(nudge)理论,展示了另一种可能性。该理论利用了人类行为中的惰性:大部分人倾向于维持默认设置,所以如果我们把 “捐献” 设为默认,人们就更可能成为捐献者。这个例子借助对人类行为的些许洞察,做了一件好事。这将是未来研究的方向。数学与社会科学的交叉点在哪里?“软科学” 是最难攻克的领域,它们是最后被数学化的学科,又或许永远无法被真正数学化。而在那些 “硬科学” 领域,我们已经取得了长足进展。数学非常适合这些学科,正因为如此,它们反而变得 “容易”。
斯托加茨的科普贡献:
著有《同步》(Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life,2003)、《微积分的人生哲学》(The Calculus of Friendship: What a Teacher and a Student Learned about Life while Corresponding about Math,2009)、《X 的奇幻之旅》(The Joy of x: A Guided Tour of Math, from One to Infinity,2012)等著作,在《纽约时报》上开设了风趣亲切的数学专栏,斯托加茨极大化解了公众对数学挥之不去的抵触情绪,在这方面,他所付出的努力鲜有人能及。
斯托加茨对数学传播的热情和投入还体现在教学风格中:注重直觉、实际应用与真实案例,自然而然地激发学生们的想象力。
凭借这些贡献,斯托加茨博士获得了无数荣誉。其中包括美国数学协会(MAA)颁发的欧拉图书奖(Euler Book Prize)、美国科学促进会(AAAS)的公众科学参与奖(Science Award)、刘易斯・托马斯科学写作奖(Lewis Thomas Prize),还有被选为剑桥大学劳斯・鲍尔(Rouse Ball)数学讲座和麻省理工学院西蒙斯(Simons)数学讲座讲师的殊荣。他目前主持着 Quanta 杂志的 The Joy of x 播客。
注释
[1] 动力系统指的是用函数描述空间中某点随时间变化的一种系统。经典例子包括钟摆的摆动、液体在管道中的流动以及人口增长。在某些动力系统中,可能会出现看似随机的行为,这种现象被称为 “混沌”,研究这一现象的数学分支就是 “混沌理论”。
[2] 复杂网络理论研究的是真实世界中以图(graph)形式表示的系统,比如 Facebook 上的好友关系或大脑中的神经连接网络。
[3]《小世界网络的集体动力学》是 Steven Strogatz 与 Duncan J. Watts 合著的一篇论文,也是有史以来被引用次数第六高的物理学论文。该论文为 “六度分隔” 这一大众熟知的概念提供了数学论证。他们提出了 “小世界网络” 这一网络类别,并被广泛应用于社会运动、南加州的地震监测站网络,以及大型数据库中的信息可用性研究。其中最著名的小世界网络构造方法就是 “沃茨–斯特罗加茨模型(Watts-Strogatz Model)”。
[4] 十二面体是一种由十二个五边形面组成的多面体。
[5] 二十面体是一种由二十个三角形面组成的多面体。
[6] 数学家常说某个命题在 “道义上成立”(morally),意思是他们根据自己对数学美感的直觉,相信这个命题 “应该是真的”。
[7] 皮埃尔 - 西蒙・拉普拉斯(Pierre-Simon Laplace)是法国著名的博学家(polymath),活跃于 18 世纪下半叶至 19 世纪上半叶。他不仅奠定了贝叶斯概率的理论基础,还发明了在现代统计物理中广泛使用的拉普拉斯变换。此外,他在天体力学方面也有重要贡献。曾有一次,为了让拉普拉斯难堪,拿破仑请他展示其太阳系模型,并质问道:“你在书中真的没有提到上帝吗?” 拉普拉斯回答:“我不需要那个假设。”
[8]“机械宇宙”(Clockwork Universe)一词,特别是启蒙时代的一些自然神论者用其描述这样一种宇宙观:宇宙如同一座机械钟表,由物理定律精密控制,可预测地运转。这个概念也被称为 “牛顿宇宙”。在这样的宇宙观中,如果存在一个掌握所有粒子的位置、速度和受力的 “拉普拉斯妖”,那么它就能预测宇宙在任意未来时刻的状态,因为每个粒子的个体状态都将根据物理定律可预测地演化。
[9] 排中律是逻辑学中的三大基本定律之一,它指出:一个命题要么是真的,要么其否定是真的。其他两个分别是:矛盾律(相互矛盾的命题不能同时为真)和同一律(每个事物都与自身同一)。这里我想问,实际上是否可以设想一个不遵守排中律的宇宙。
[10] 大洋国是乔治・奥威尔小说《1984》中的三个虚构的超级国家之一。在小说设定中,这些国家始终处于战争状态,以此消耗失控的资本主义不断产生的过剩供给。
[11] 理查德・塞勒(Richard Thaler)是芝加哥大学布斯商学院的行为经济学家,他因将心理学纳入个体决策的经济分析而获得了 2017 年诺贝尔经济学奖。此处引用的是他的著作《助推》(Nudge: Improving Decisions About Health, Wealth, and Happiness),书中提出,组织可以通过 “助推”(Nudge)策略优化政策设计,让成员更容易做出好决策,更难做出坏决策。一个典型的例子是将器官捐赠设为 “默认捐献”,指除非一个人在生前明确拒绝捐献器官,否则在死后会被默认为器官捐献者。
采访者简介
Prashanth Ramakrishna是一位作家、研究员和学生。他在纽约大学攻读应用数学和网络安全专业,研究课题包括分析青春期大鼠的睡眠周期,以及设计规则随游戏进程演变的变体国际象棋等。除了沉浸于符号的世界,他还热衷于有趣的对话。
本文已获得作者授权翻译并发表于《返朴》。
原文译自 Prashanth Ramakrishna, An Interview with Steven Strogatz.
https://www.thebeliever.net/logger/an-interview-with-steven-strogatz/
远山启:微积分究竟是什么?
图灵编辑部 2025年09月04日 10:29 北京
一、引言
在数学教育领域,传授知识与培养思维方法具有同等重要的地位。正如日本学者远山启所言:教育所必须做的事情之一,就是教会学生如何从众多方法中选出最便于思考的那种方法。这里说的便于思考,并非仅指对于孩子来说方便使用,更重要的是,孩子在将来也能独立使用同样的思考方法。也就是说,作为教育者的成年人,应当去寻找具有发展性的思考方法来教授,这是教育的一项重要任务。
微积分作为近代数学的核心内容,其思想方法源于对复杂问题的简化与重构,并非传统认知中晦涩难懂的概念。本文将基于远山启在《数学与生活 5:数学的历史、现代与方法》中关于“近代数学”的相关内容,系统阐述微积分的本质、发展历程及其科学价值。
二、微分与积分的本质
2.1 微积分与笛卡儿原则的关联
微积分的核心思想隐含于笛卡儿四条原则中的第二条与第三条,二者共同构成了微积分的方法论基础:
- 笛卡儿第二条原则与微分:研究复杂问题时,将其尽可能分割为若干小部分,使难题简化。这一“分析”过程对应微积分中的“微分”——如其字面含义,将研究对象分割为微小部分。笛卡儿对此的表述为:“对于我要研究的每一个难题,在必要的限度下将其尽可能多地分割为若干小部分,以便更好地解决它们。”
- 笛卡儿第三条原则与积分:将分割后的细小部分重新连接组合,以还原问题的整体。这一“综合”过程对应微积分中的“积分”——即“积累”分割部分,重建研究对象的整体属性。
2.2 微分的核心构想:复杂到简单的近似
以曲线研究为例(如图 1-1 所示),曲线本身是复杂的几何形态,但通过“细分-近似”的逻辑可实现简化:
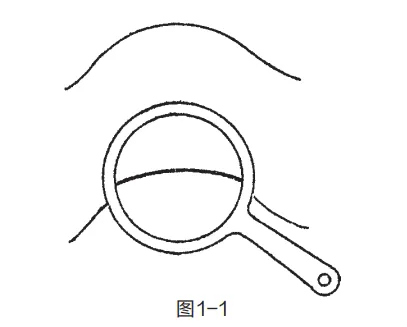
- 对曲线进行细致分割后,取其中任意一小段观察,该小段会近似于直线;
- 分割精度越高(即小段长度越短),近似程度越高——如同用放大镜、显微镜甚至电子显微镜观察曲线小段,倍率越高,观察到的部分越接近直线;
- 直线作为简单、易处理的几何对象,可通过已有的直线相关知识进行分析,从而降低曲线研究的难度。
2.3 积分的核心作用:局部到整体的还原
微分的“细分”过程存在局限性——分割精度越高,观察范围越狭小,仅能反映研究对象的局部属性。为弥补这一缺陷,需通过“积分”将无数细小的局部部分重新连接、组合,最终还原研究对象的整体特征。
综上,微积分的思考方法具有显著的自然性:通过微分将复杂对象“化繁为简”,通过积分将局部结果“积少成多”,二者结合实现对复杂问题的完整求解。
三、微积分的发展历程:牛顿与莱布尼茨之争
3.1 核心人物与时间线
微积分的正式创立源于 17 世纪两位学者的独立研究,其关键信息如下表所示:
| 人物 | 生卒年份 | 核心贡献 | 时间线特征 |
|---|---|---|---|
| 艾萨克·牛顿(Isaac Newton) | 1643—1727 | 独立创立微积分,构建牛顿力学体系 | 研究启动早,成果未及时公开发表 |
| 戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz) | 1646—1716 | 独立创立微积分,完善符号系统 | 研究启动晚于牛顿(约 10 余年),成果公开及时 |
3.2 争端的起源与演变
- 初期关系:牛顿与莱布尼茨早期保持良好学术交流,牛顿曾在书信中提及:“发明微分与积分者,唯有你和我。”
- 争端爆发原因:
- 牛顿虽早于莱布尼茨创立微积分,但长期未公开发表成果;
- 莱布尼茨公开发表成果后,牛顿认为其“剽窃”自身思想,引发学术争议;
- 深层原因:二人最初均未意识到微积分的重大科学价值,后期随着微积分在数学、物理领域的应用拓展,其“发明权”的象征意义与学术地位关联增强,导致争端升级。
- 历史结论:现代数学史公认二者为微积分的“共同独立发明者”——牛顿侧重从物理问题(如天体运动)出发构建微积分,莱布尼茨侧重从数学逻辑出发完善体系,且后者设计的符号系统(如“ d x \mathrm{d}x dx”“ ∫ \int ∫”)至今仍被广泛使用。
四、微积分的科学价值
4.1 对现代科学体系的支撑作用
微积分的诞生为现代数学、天文学、物理学的发展提供了核心工具,其具体影响如下:
- 数学领域:推动数学从“常量数学”(如代数、几何)向“变量数学”(如分析学)跨越,若没有微积分,现代数学的发展程度可能仅为当前的 1/3;
- 天文学与物理学领域:成为构建天体运动规律、经典力学体系的基础——若无微积分,牛顿无法推导万有引力定律,开普勒定律也难以与力学理论结合。
4.2 微积分与开普勒定律的关联
约翰尼斯·开普勒(Johannes Kepler)基于其老师第谷·布拉赫(Tycho Brahe,1546—1601)的天文观测数据,提出了行星运动三大定律,而微积分则成为连接开普勒定律与牛顿力学的关键桥梁。
4.2.1 开普勒三大定律的核心内容
- 开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道为椭圆,太阳位于椭圆的一个焦点上。
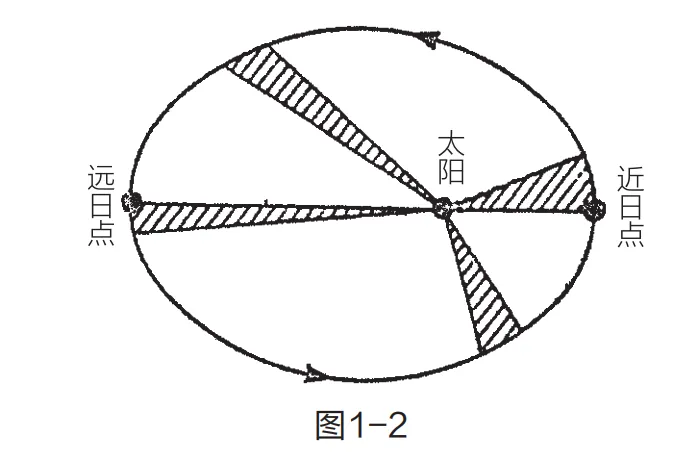
- 开普勒第二定律(面积定律):行星与太阳的连线在相等时间内扫过相等的面积(如图 1-2 所示)——由此可推知:行星离太阳越远,运动速度越慢;离太阳越近,运动速度越快。
- 开普勒第三定律(周期定律):行星绕太阳公转周期的平方与其椭圆轨道半长轴的立方成正比,数学表达式为 T 2 ∝ a 3 T^2 \propto a^3 T2∝a3(其中 T T T 为公转周期, a a a 为轨道半长轴),该定律同样适用于人造地球卫星。
4.2.2 微积分对开普勒定律的“转译”
- 开普勒定律的本质:属于“积分定律”,需通过长期观测(如行星完整公转一周)获取整体数据,才能描述行星运动规律;
- 牛顿力学的突破:通过微分将开普勒定律“转译”为“微分定律”——即描述行星在“瞬间”的运动状态(如速度、加速度),其核心成果为“万有引力定律”:太阳与行星间的引力大小与二者距离的平方成反比,数学表达式为 F ∝ 1 r 2 F \propto \frac{1}{r^2} F∝r21(其中 F F F 为引力, r r r 为二者距离);
- 二者的一致性:将牛顿的万有引力定律(微分定律)通过积分运算还原,可得到开普勒三大定律(积分定律),证明二者在物理本质上完全一致,仅表述维度不同。
4.3 微积分在科学预测中的应用
牛顿力学与微积分的结合,使科学首次具备“精准预测未来现象”的能力,典型案例包括:
- 日食预测:可精确计算日食发生的时间(如“某年某月某日某时某分”)、持续时长(如“几分钟几秒”),且预测结果可通过观测实证;
- 天体运动预测:如预测行星的位置、彗星的回归周期(如哈雷彗星)等。
这种“预测能力”是近代科学区别于传统经验科学的关键特征,也使“数学工具”在科学研究中的核心地位得以确立。
4.4 微积分的局限性
需注意,微积分的“精准预测”能力依赖于研究对象的“单纯性”:
- 太阳系天体运动的规律较为单纯(仅受引力主导,干扰因素少),因此微积分可充分发挥作用;
- 对于复杂系统(如“纸片掉落轨迹”——受重力、空气阻力、气流等多因素影响),需结合更复杂的数学工具(如微分方程、流体力学),且预测精度会受系统复杂度限制。
五、结论
近代数学以笛卡儿的方法论为起点,以牛顿、莱布尼茨创立的微积分为核心,实现了数学思想与科学工具的重大突破。微积分的本质并非“晦涩的公式集合”,而是“化繁为简、积少成多”的思维方法——通过微分将复杂对象分割为可处理的局部,通过积分将局部结果还原为整体规律。
这种方法不仅支撑了牛顿力学、天体运动规律等重大科学发现,更推动了现代科学从“定性描述”向“定量分析”的跨越,成为人类理解自然、预测未来的“精巧镜头”。正如远山启所强调的,数学教育的核心在于传递这类“具有发展性的思考方法”,而微积分正是这一理念的典型载体。
来源 | 《数学与生活5:数学的历史、现代与方法》
作者 | [日]远山启
译者 | 武晓宇
书中以“古代数学—中世纪数学—近代数学—现代数学”为脉络,结合日常经验阐述数学概念与思想的发展,通俗解读现代数学的重要方法,引导读者建立对数学的深刻理解。
via:
-
牛顿与莱布尔茨的微积分战争 杰森苏格拉底巴迪 算法与数学之美 2022 年 07 月 07 日 20:32 北京
https://mp.weixin.qq.com/s/hKOEp2ii3L7RKw9JmAmKiA -
微积分的前奏:从列奥纳多到哈里奥特
https://mp.weixin.qq.com/s/fc5W9UNzeNxDhPGFlksZJw -
从积分法的诞生到牛顿归纳出微积分学竟然经历了 1800 年!一文讲透微积分的本质 原创 神永正博 图灵新知 2023 年 05 月 31 日 19:00 北京
https://mp.weixin.qq.com/s/W-9VisCN835ZnAzxp04Vlw -
在无限与变化之间:一场关于微积分的深度对话
https://mp.weixin.qq.com/s/rLxD4Bbh8OFnr6bMv79luA -
远山启:微积分究竟是什么?
https://mp.weixin.qq.com/s/uVSk82hCo-tirycCzG4weA






















 2269
2269

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








