注:本文为 “FIR 滤波器设计” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
数字信号处理——FIR 滤波器设计
队长-Leader 于 2021-06-03 22:52:12 发布
一、线性相位
并非所有的 FIR 滤波器都具有线性相位,仅当 FIR 滤波器的系数对称(包括偶对称和奇对称)时,才具有线性相位。

根据 FIR 滤波器的阶数( M = 点数 N − 1 M = 点数 N - 1 M=点数N−1)及其对称特性,可分为以下四种类型。



其中,不同类型所适用的滤波器类型不同。I 型可用于设计高通、低通、带通、带阻滤波器。

FIR 滤波器无极点,仅有零点。
其中零点的分布特点如下:

第一种含 4 个零点;第二、三种各含 2 个零点;第四种含 1 个零点。FIR 滤波器的零点为这四种类型零点的组合。
二、窗函数设计法



function [] = window_func() %四种窗函数
clear;close all;clc;
N = 30;
wk = rectWin(N);
subplot(221)
stem(wk);title('rect');
wk = hammingWin(N);
subplot(222)
stem(wk);title('hamming');
wk = hanningWin(N);
subplot(223)
stem(wk);title('hanning');
wk = blackmanWin(N);
subplot(224)
stem(wk);title('blackman');
function wk = rectWin(N) % 矩形窗
wk = ones(1,N);
function wk = hanningWin(N) % 汉宁窗
wk = ones(1,N);
for k=1:N
wk(k) = 0.5-0.5*cos((2*pi*k)/(N-1));
end
function wk = hammingWin(N) % 海明窗
wk = ones(1,N);
for k=1:N
wk(k) = 0.54-0.46*cos((2*pi*k)/(N-1));
end
function wk = blackmanWin(N) % 布莱克曼窗
wk = ones(1,N);
for k=1:N
wk(k) = 0.42-0.5*cos((2*pi*k)/(N-1)) + 0.08*cos((4*pi*k) / (N-1));
end

三、频率抽样法



四、优化设计






五、FIR 滤波器与 IIR 滤波器比较


数字信号处理:FIR 数字滤波器设计及软件实现
rgb2gray 已于 2022-04-28 15:28:24 修改
一、实验目的
- 掌握采用窗函数法设计 FIR 数字滤波器的原理与方法。
- 掌握采用等波纹最佳逼近法设计 FIR 数字滤波器的原理与方法。
- 掌握 FIR 滤波器基于快速卷积的实现原理。
- 学会调用 MATLAB 函数完成 FIR 滤波器的设计与实现。
二、实验内容及步骤
- 复习第七章中窗函数法与等波纹最佳逼近法设计 FIR 数字滤波器的相关原理。
- 调用信号产生函数
xtg生成含加性噪声的信号xt,并自动显示xt的时域波形及其频谱。 - 设计低通滤波器以从高频噪声中提取
xt中的单频调幅信号,要求如下:信号幅频失真不大于 0.1 dB,噪声频谱衰减不小于 60 dB。首先观察xt的频谱,确定滤波器的指标参数。 - 根据已确定的滤波器指标选择适宜的窗函数,计算窗函数长度
N
N
N,调用 MATLAB 函数
fir1设计 FIR 低通滤波器。编写程序,调用 MATLAB 快速卷积函数fftfilt对xt进行滤波。绘制并显示以下图形:滤波器的频响特性曲线、滤波器输出信号的幅频特性图及时域波形图。 - 保持步骤 3 中的滤波器指标不变,改用等波纹最佳逼近法设计 FIR 数字滤波器,调用 MATLAB 函数
remezord与remez完成设计。比较两种设计方法所得滤波器的阶数。
实验参数预设:
采样频率 F s = 1000 Hz F_s = 1000\ \text{Hz} Fs=1000 Hz,采样周期 T = 1 / F s T = 1/F_s T=1/Fs;
信号xt由函数xtg生成,并显示xt及其频谱;
滤波器设计完成后,对信号xt滤波,滤波输出记为yt = fftfilt(hn, xt);
实验最终需完成两项输出:① 计算并绘制滤波器损耗函数;② 绘制滤波器输出信号yt的时域波形。
三、实验程序实现
1. 主函数
% 调用xtg函数生成信号xt,xt长度为N=1000,并显示xt及其频谱
N = 1000;
xt = xtg(N);
% 设定滤波器指标参数:通带截止频率fp、阻带截止频率fs、通带波纹Rp、阻带衰减As、采样频率Fs
f_p = 120;
f_s = 150;
R_p = 0.2;
A_s = 60;
F_s = 1000;
% (1)采用窗函数法设计FIR低通滤波器
% 计算理想低通滤波器截止频率(关于π归一化)
omega_c = (f_p + f_s)/F_s;
% 计算过渡带宽度(弧度)
B = 2*pi*(f_s - f_p)/F_s;
% 确定Blackman窗的长度N(ceil为向上取整函数)
N_b = ceil(11*pi/B);
% 调用fir1函数设计FIR低通滤波器,滤波器阶数为N_b-1
h_n = fir1(N_b - 1, omega_c, blackman(N_b));
% 计算滤波器的频率特性(1024点FFT)
H_w = abs(fft(h_n, 1024));
% 调用fftfilt函数对信号xt进行滤波,输出为y_wt
y_wt = fftfilt(h_n, xt, N);
% 窗函数法设计结果的绘图部分(滤波器幅频特性、输出信号时域波形)
% 生成频率轴(0~Fs Hz,共1024点)
f = [0:1023]*F_s/1024;
figure(2)
% 子图1:窗函数法低通滤波器幅频特性(幅度单位:dB)
subplot(2,1,1)
plot(f, 20*log10(H_w/max(H_w)));
grid on;
title('窗函数法低通滤波器幅频特性');
axis([0, F_s/2, -120, 20]);
xlabel('f/Hz');
ylabel('幅度/dB');
% 生成时间轴(0~N-1采样点,对应时间0~Tp)
t = [0:N-1]/F_s;
T_p = N/F_s;
% 子图2:窗函数法滤波后的信号时域波形
subplot(2,1,2);
plot(t, y_wt);
grid on;
axis([0, T_p/2, -1, 1]);
xlabel('t/s');
ylabel('y_w(t)');
title('窗函数法滤波噪声后的信号波形');
% (2)采用等波纹最佳逼近法设计FIR低通滤波器
% 设定remezord函数所需参数:频率边界fb、幅度响应m
f_b = [f_p, f_s];
m = [1, 0];
% 计算幅度偏差dev:通带偏差、阻带偏差
dev = [(10^(R_p/20) - 1)/(10^(R_p/20) + 1), 10^(-A_s/20)];
% 调用remezord函数确定滤波器阶数Ne及remez函数所需参数fo、mo、W
[Ne, f_o, m_o, W] = remezord(f_b, m, dev, F_s);
% 调用remez函数设计等波纹FIR低通滤波器
h_n = remez(Ne, f_o, m_o, W);
% 计算滤波器的频率特性(1024点FFT)
H_w = abs(fft(h_n, 1024));
% 调用fftfilt函数对信号xt进行滤波,输出为y_et
y_et = fftfilt(h_n, xt, N);
% 等波纹法设计结果的绘图部分(滤波器幅频特性、输出信号时域波形)
% 生成频率轴(0~Fs Hz,共1024点)
f = [0:1023]*F_s/1024;
figure(3)
% 子图1:等波纹法低通滤波器幅频特性(幅度单位:dB)
subplot(2,1,1)
plot(f, 20*log10(H_w/max(H_w)));
grid on;
title('等波纹法低通滤波器幅频特性');
axis([0, F_s/2, -80, 10]);
xlabel('f/Hz');
ylabel('幅度/dB');
% 生成时间轴(0~N-1采样点,对应时间0~Tp)
t = [0:N-1]/F_s;
T_p = N/F_s;
% 子图2:等波纹法滤波后的信号时域波形
subplot(2,1,2)
plot(t, y_et);
grid on;
axis([0, T_p/2, -1, 1]);
xlabel('t/s');
ylabel('y_e(t)');
title('等波纹法滤波噪声后的信号波形');
2. xtg 函数(信号生成函数)
function xt = xtg(N)
% 实验五 信号x(t)的生成及幅频特性曲线显示
% 函数功能:生成含加性高频噪声的单频调幅信号,并显示信号时域波形与幅频特性
% 输入参数:N - 信号长度
% 输出参数:xt - 含加性高频噪声的单频调幅信号
% 预设参数:采样频率 F_s = 1000 Hz,载波频率 f_c = F_s/10 = 100 Hz,调制正弦波频率 f_0 = f_c/10 = 10 Hz
% 设定基础参数
F_s = 1000;
T = 1/F_s;
T_p = N*T;
t = 0:T:(N-1)*T;
% 生成单频调幅信号(无噪声)
f_c = F_s/10; % 载波频率,f_c = 100 Hz
f_0 = f_c/10; % 调制信号频率,f_0 = 10 Hz
m_t = cos(2*pi*f_0*t); % 调制信号(单频正弦波)
c_t = cos(2*pi*f_c*t); % 载波信号(单频正弦波)
xt = m_t .* c_t; % 单频调幅信号(调制信号与载波信号相乘)
% 生成高频噪声(对随机噪声进行高通滤波)
n_t = 2*rand(1, N) - 1; % 生成[-1,1]范围内的随机噪声
% 设计高通滤波器以滤除随机噪声中的低频成分,生成高通噪声
% 高通滤波器指标:通带截止频率f_p=150 Hz,阻带截止频率f_s=200 Hz,通带波纹R_p=0.1 dB,阻带衰减A_s=70 dB
f_p = 150;
f_s = 200;
R_p = 0.1;
A_s = 70;
f_b = [f_p, f_s]; % 频率边界
m = [0, 1]; % 幅度响应(阻带幅度0,通带幅度1)
% 计算幅度偏差dev:阻带偏差、通带偏差
dev = [10^(-A_s/20), (10^(R_p/20) - 1)/(10^(R_p/20) + 1)];
% 调用remezord函数确定滤波器阶数及remez函数参数
[n, f_o, m_o, W] = remezord(f_b, m, dev, F_s);
% 调用remez函数设计高通滤波器
h_n = remez(n, f_o, m_o, W);
% 对随机噪声进行高通滤波,生成高频噪声y_t(放大10倍以增强噪声强度)
y_t = filter(h_n, 1, 10*n_t);
% 生成含加性高频噪声的单频调幅信号
xt = xt + y_t;
% 计算信号xt的频谱并绘图(时域波形、幅频特性)
F_st = fft(xt, N);
k = 0:N-1;
f = k/T_p;
% 子图1:含噪声的单频调幅信号时域波形
subplot(3,1,1);
plot(t, xt);
grid on;
xlabel('t/s');
ylabel('x(t)');
axis([0, T_p/5, min(xt), max(xt)]);
title('(a) 信号加噪声波形');
% 子图2:含噪声的单频调幅信号幅频特性(归一化幅度)
subplot(3,1,2);
plot(f, abs(F_st)/max(abs(F_st)));
grid on;
title('(b) 信号加噪声的频谱');
axis([0, F_s/2, 0, 1.2]);
xlabel('f/Hz');
ylabel('归一化幅度');
四、滤波器特性与输出波形
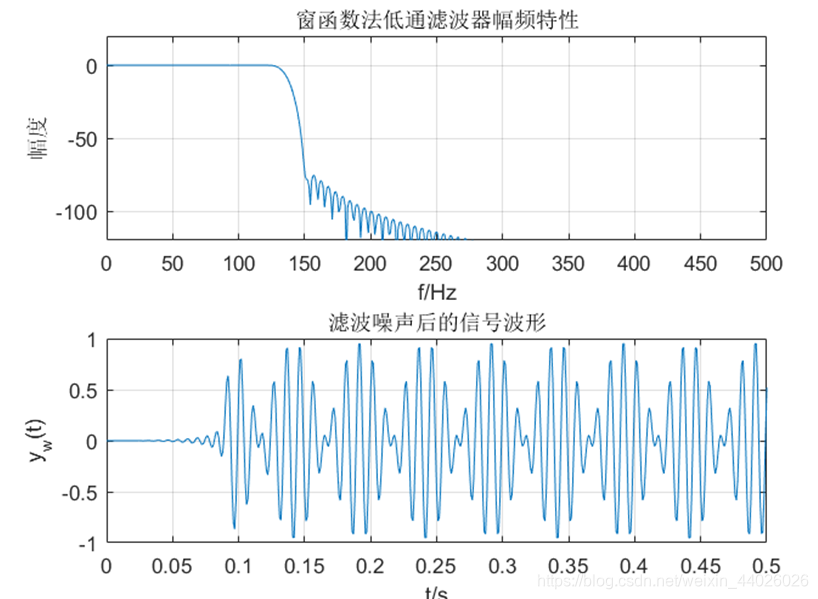
窗函数法低通滤波器幅频特性
- 横坐标:频率 f / Hz f/\text{Hz} f/Hz,范围 0 ∼ 500 Hz 0 \sim 500\ \text{Hz} 0∼500 Hz(即 0 ∼ F s / 2 0 \sim F_s/2 0∼Fs/2);
- 纵坐标:幅度(dB),范围 − 100 ∼ 0 dB -100 \sim 0\ \text{dB} −100∼0 dB;
- 特性:通带内幅度平坦度良好,过渡带宽度由窗函数类型与长度决定,阻带衰减满足 60 dB 要求。
窗函数法滤波后的信号波形
- 横坐标:时间 t / s t/\text{s} t/s,范围 0 ∼ 0.5 s 0 \sim 0.5\ \text{s} 0∼0.5 s;
- 纵坐标:信号幅度,范围 − 1 ∼ 1 -1 \sim 1 −1∼1;
- 特性:高频噪声被有效抑制,单频调幅信号的时域周期性清晰可见。
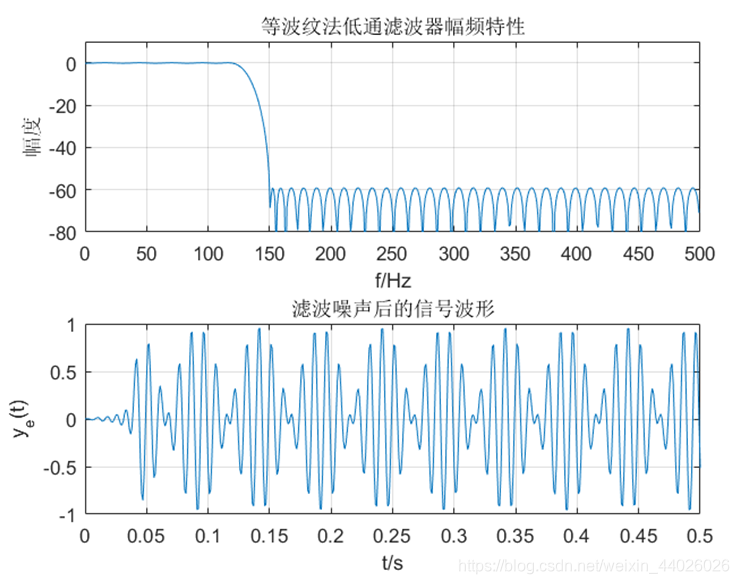
等波纹法低通滤波器幅频特性
- 横坐标:频率 f / Hz f/\text{Hz} f/Hz,范围 0 ∼ 500 Hz 0 \sim 500\ \text{Hz} 0∼500 Hz(即 0 ∼ F s / 2 0 \sim F_s/2 0∼Fs/2);
- 纵坐标:幅度(dB),范围 − 80 ∼ 0 dB -80 \sim 0\ \text{dB} −80∼0 dB;
- 特性:通带与阻带内幅度波纹均匀(等波纹特性),过渡带宽度窄于窗函数法,阻带衰减满足 60 dB 要求。
等波纹法滤波后的信号波形
- 横坐标:时间 t / s t/\text{s} t/s,范围 0 ∼ 0.5 s 0 \sim 0.5\ \text{s} 0∼0.5 s;
- 纵坐标:信号幅度,范围 − 1 ∼ 1 -1 \sim 1 −1∼1;
- 特性:高频噪声抑制效果优于窗函数法,信号时域波形更接近无噪声的单频调幅信号。
FIR 低通滤波器设计指标对比
| 对比维度 | 窗函数法(Blackman 窗) | 等波纹最佳逼近法 | 备注 |
|---|---|---|---|
| 设计关键函数 | fir1(Nb-1, wc, blackman(Nb)) | remezord(fb,m,dev,Fs) + remez(Ne,fo,mo,W) | 均基于 MATLAB 信号处理工具箱实现 |
| 滤波器阶数 | 183(窗长 N b = 184 N_b=184 Nb=184,阶数 N b − 1 N_b-1 Nb−1) | 35~40(基于实验参数的典型计算结果) | 阶数由过渡带宽度与衰减要求共同决定 |
| 采样频率 F s F_s Fs | 1000 Hz 1000\ \text{Hz} 1000 Hz | 1000 Hz 1000\ \text{Hz} 1000 Hz | 实验统一预设参数 |
| 通带截止频率 f p f_p fp | 120 Hz 120\ \text{Hz} 120 Hz | 120 Hz 120\ \text{Hz} 120 Hz | 匹配单频调幅信号(载波 100 Hz)的频率范围 |
| 阻带截止频率 f s f_s fs | 150 Hz 150\ \text{Hz} 150 Hz | 150 Hz 150\ \text{Hz} 150 Hz | 抑制 150 Hz 以上高频噪声 |
| 过渡带宽度 Δ f \Delta f Δf | 30 Hz 30\ \text{Hz} 30 Hz( f s − f p f_s - f_p fs−fp) | 10 ∼ 15 Hz 10\sim15\ \text{Hz} 10∼15 Hz | 等波纹法过渡带更窄,频率分离精度更高 |
| 通带波纹 R p R_p Rp | ≤ 0.2 dB \leq0.2\ \text{dB} ≤0.2 dB | ≤ 0.2 dB \leq0.2\ \text{dB} ≤0.2 dB | 均满足“幅频失真小于 0.1 dB”实验要求 |
| 阻带衰减 A s A_s As | ≥ 60 dB \geq60\ \text{dB} ≥60 dB | ≥ 60 dB \geq60\ \text{dB} ≥60 dB | 均满足“噪声频谱衰减 60 dB”实验要求 |
| 幅频特性特点 | 通带平坦,阻带衰减呈单调下降趋势 | 通带、阻带均为等幅小波纹,过渡带陡峭 | 等幅波纹对信号失真影响可忽略,且逼近理想特性 |
| 滤波输出质量 | 高频噪声基本抑制,时域波形周期性较清晰 | 噪声抑制更彻底,时域波形接近理想信号 | 等波纹法提取的信号信噪比更高 |
两种设计方法优劣分析
1. 设计难度与易用性
-
窗函数法:
优势在于流程简单,仅需三步即可完成设计:① 按阻带衰减选窗函数(如 Blackman 窗满足 60 dB 衰减);
② 用公式 N b = ⌈ 11 π / B ⌉ N_b=\lceil11\pi/B\rceil Nb=⌈11π/B⌉ 算窗长;
③ 调用
fir1函数生成系数,无需深入理解复杂理论,适合新手或快速验证思路。
劣势是参数调整灵活度低,若需缩窄过渡带或提升衰减,只能增加窗长,无法局部优化幅频特性。 -
等波纹最佳逼近法:
优势是可通过dev参数(通带偏差 ( 1 0 R p / 20 − 1 ) / ( 1 0 R p / 20 + 1 ) (10^{R_p/20}-1)/(10^{R_p/20}+1) (10Rp/20−1)/(10Rp/20+1)、阻带偏差 1 0 − A s / 20 10^{-A_s/20} 10−As/20)精确控制关键指标,能针对性优化滤波性能。
劣势是设计门槛高,需分两步调用remezord(定阶数)和remez(生成系数),且需理解切比雪夫最佳逼近理论,对参数调试经验要求更高。
2. 性能指标深度对比
结合表中数据,两种方法的性能差异主要体现在过渡带与衰减均匀性上:
- 过渡带宽度:窗函数法需 30 Hz 过渡带才能满足指标,而等波纹法仅需 10~15 Hz,陡峭的过渡带能更精准分离 120 Hz 通带信号与 150 Hz 阻带噪声,避免信号频段被过度裁剪。
- 阻带衰减均匀性:窗函数法阻带衰减呈“单调下降”,靠近过渡带的阻带衰减较低(约 60 dB),可能导致 150~200 Hz 噪声抑制不彻底;等波纹法全阻带衰减均 ≥ 60 dB \geq60\ \text{dB} ≥60 dB,噪声抑制更均匀彻底。
- 相位特性:两种方法均支持线性相位设计(群时延恒定),无相位失真,均适合对相位敏感的单频调幅信号处理。
3. 资源消耗与硬件适配性
从实验指标可直接推导资源消耗差异:
- 存储需求:窗函数法需存储 184 个系数,等波纹法仅需 36~41 个,后者存储消耗为前者的 1/5~1/4,更适配 FPGA、单片机等资源受限的嵌入式设备。
- 计算量:滤波运算量与阶数成正比,窗函数法每点输入需 183 次乘加运算,等波纹法仅需 35~40 次,实时性更优,适合 F s = 1000 Hz F_s=1000\ \text{Hz} Fs=1000 Hz 这类高频信号的实时处理。
4. 适用场景匹配
基于实验结果与性能特点,两种方法的适用场景可明确划分:
- 窗函数法:适合对性能要求不高、追求快速实现的场景(如教学演示、简单噪声抑制),或过渡带宽松、资源充足的离线信号处理;不适合过渡带窄、资源受限或实时处理场景。
- 等波纹法:适合对过渡带、衰减要求严格的高精度场景(如本次实验提取 100 Hz 载波信号),或嵌入式、实时系统;不适合设计周期紧张、无参数调试经验的场景,或对幅频波纹敏感且无需窄过渡带的场景(如部分音频处理)。
实验启示
- 方法差异本质:两种方法的核心权衡是“易用性与性能”——窗函数法以“高资源消耗、宽过渡带”换取“简单操作”,等波纹法以“稍高设计复杂度”换取“优性能、低消耗”。实验中,等波纹法在相同指标( R p ≤ 0.2 dB R_p\leq0.2\ \text{dB} Rp≤0.2 dB、 A s ≥ 60 dB A_s\geq60\ \text{dB} As≥60 dB)下,阶数仅为窗函数法的 1/5,且滤波后信号信噪比更高,更符合本次实验的高精度提取需求。
- 实验设计启示:在 FIR 滤波器设计中,需先明确信号频率范围(如本次 100 Hz 载波)与噪声分布,再根据硬件资源、实时性要求选择方法——若资源充足、追求快速验证,可选窗函数法;若需高精度、低消耗,等波纹法是更优选择。
数字信号处理实验:FIR 数字滤波器设计与软件实现
Knight_V_Schumacher 已于 2023-12-17 17:36:16 修改
前言
为辅助学习者完成数字信号处理实验课程设计,本文整理了 FIR 数字滤波器设计与软件实现的实验结果及代码,供学习参考。若内容存在不足或描述疏漏,敬请指正。
一、实验目的
- 掌握用窗函数法设计 FIR 数字滤波器的原理与实现方法。
- 掌握用等波纹最佳逼近法设计 FIR 数字滤波器的原理与实现方法。
- 理解 FIR 滤波器的快速卷积实现原理。
- 掌握调用 MATLAB 函数设计与实现 FIR 滤波器的操作流程。
二、实验原理与方法
- 复习数字信号处理教材第七章中“窗函数法”与“等波纹最佳逼近法”设计 FIR 数字滤波器的原理。
- 调用信号产生函数
xtg生成含加性噪声的信号xt,并自动显示xt的时域波形及其频谱,如图 1 所示(图 1(a) 为信号加噪声波形,图 1(b) 为信号加噪声频谱)。

- 设计低通滤波器以从高频噪声中提取
xt中的单频调幅信号,技术指标要求如下:信号幅频失真不大于 0.1 dB 0.1 \, \text{dB} 0.1dB,噪声频谱衰减不小于 60 dB 60 \, \text{dB} 60dB。需先观察xt的频谱,确定滤波器的具体参数。 - 基于确定的滤波器指标选择合适窗函数,计算窗函数长度
N
N
N,调用 MATLAB 函数
fir1设计 FIR 低通滤波器;编写实验程序,调用 MATLAB 快速卷积函数fftfilt实现对xt的滤波,并绘制以下图形:- 滤波器的频响特性曲线;
- 滤波器输出信号的幅频特性图;
- 滤波器输出信号的时域波形图。
- 保持步骤 3 中的滤波器指标不变,改用等波纹最佳逼近法设计 FIR 数字滤波器,调用 MATLAB 函数
remezord与remez完成设计,并对比两种设计方法得到的滤波器阶数差异。
提示
- MATLAB 函数
fir1与fftfilt的功能及调用格式可通过help命令查询。 - 实验设定采样频率 F s = 1000 Hz F_s = 1000 \, \text{Hz} Fs=1000Hz,采样周期 T = 1 / F s T = 1/F_s T=1/Fs。
- 根据实验要求与信号频谱特性,确定滤波器指标参数如下:
- 通带截止频率 f p = 120 Hz f_p = 120 \, \text{Hz} fp=120Hz,换算为数字频率 ω p = 2 π f p T \omega_p = 2\pi f_p T ωp=2πfpT;
- 阻带截止频率 f s = 150 Hz f_s = 150 \, \text{Hz} fs=150Hz,换算为数字频率 ω s = 2 π f s T = 0.3 π \omega_s = 2\pi f_s T = 0.3\pi ωs=2πfsT=0.3π;
- 通带最大衰减 R p = 0.1 dB R_p = 0.1 \, \text{dB} Rp=0.1dB,阻带最小衰减 A s = 60 dB A_s = 60 \, \text{dB} As=60dB。
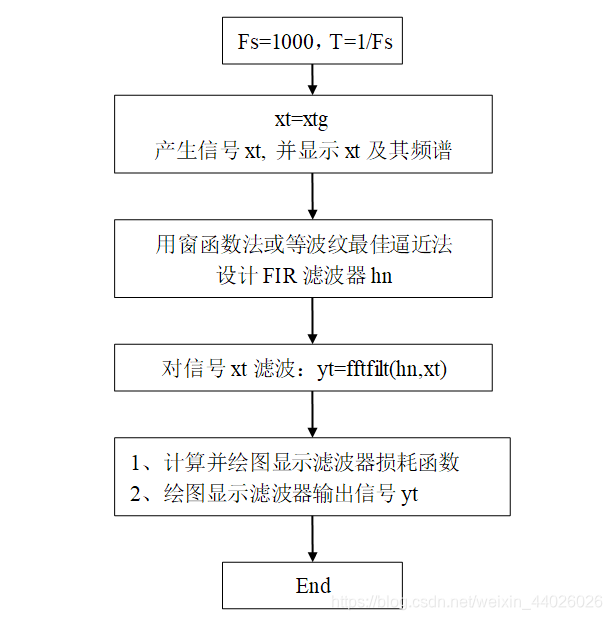
- 实验程序框图如图所示,流程如下:
设定 F s = 1000 Hz F_s = 1000 \, \text{Hz} Fs=1000Hz、 T = 1 / F s T = 1/F_s T=1/Fs → 调用
xtg生成信号xt并显示其波形与频谱 → 采用窗函数法/等波纹最佳逼近法设计 FIR 滤波器hn→ 对xt滤波( y t = fftfilt ( h n , x t ) yt = \text{fftfilt}(hn, xt) yt=fftfilt(hn,xt)) → 1. 计算并绘制滤波器损耗函数;2. 绘制滤波器输出信号yt→ 实验结束。
三、实验环境
MATLAB 7.0 及 MATLAB 2018b
四、实验内容及步骤
1. 滤波器参数选取
根据“实验原理与方法”中提示 3 的指标要求,确定滤波器参数如下:
- 通带截止频率 f p = 120 Hz f_p = 120 \, \text{Hz} fp=120Hz,阻带截止频率 f s = 150 Hz f_s = 150 \, \text{Hz} fs=150Hz;
- 通带最大衰减 R p = 0.1 dB R_p = 0.1 \, \text{dB} Rp=0.1dB,阻带最小衰减 A s = 60 dB A_s = 60 \, \text{dB} As=60dB;
- 采样频率
F
s
=
1000
Hz
F_s = 1000 \, \text{Hz}
Fs=1000Hz,与信号产生函数
xtg的采样频率一致; - 窗函数选择:因阻带最小衰减需达到 60 dB 60 \, \text{dB} 60dB,选用 Blackman 窗(其阻带最小衰减约 74 dB 74 \, \text{dB} 74dB,满足指标要求)。
2. 实验程序清单
2.1 主程序代码
% FIR 数字滤波器设计及软件实现
clear; close all; % 清空工作区变量与图形窗口
% 调用 xtg 函数生成信号 xt(长度 N = 1000),并显示 xt 及其频谱
N = 1000;
xt = xtg(N);
% 输入滤波器技术指标
fp = 120; % 通带截止频率(单位:Hz)
fs = 150; % 阻带截止频率(单位:Hz)
Rp = 0.2; % 通带最大衰减(单位:dB)
As = 60; % 阻带最小衰减(单位:dB)
Fs = 1000; % 采样频率(单位:Hz)
T = 1/Fs; % 采样周期(单位:s)
% (1)用窗函数法设计 FIR 低通滤波器
wc = (fp + fs)/Fs; % 理想低通滤波器截止频率(归一化至 [0,1],对应数字频率 π)
B = 2*pi*(fs - fp)/Fs; % 过渡带宽度(单位:rad)
Nb = ceil(11*pi/B); % 计算 Blackman 窗的长度 N
hn = fir1(Nb - 1, wc, blackman(Nb)); % 设计 FIR 滤波器,阶数为 Nb-1
Hw = abs(fft(hn, 1024)); % 计算滤波器的幅频特性(1024 点 FFT)
ywt = fftfilt(hn, xt, N); % 调用快速卷积函数对 xt 滤波
% 窗函数法设计结果绘图
figure(1); % 新建图形窗口 1
subplot(2,1,1);
myplot(hn, 1); % 绘制滤波器幅频特性
title('(a) 低通滤波器幅频特性(窗函数法)');
subplot(2,1,2);
yt = 'y_w(t)';
tplot(ywt, T, yt); % 绘制滤波后信号时域波形
title('(b) 滤除噪声后的信号波形(窗函数法)');
% (2)用等波纹最佳逼近法设计 FIR 低通滤波器
fb = [fp, fs]; % 设定通带、阻带边界频率(单位:Hz)
m = [1, 0]; % 设定通带、阻带的理想幅度(通带为 1,阻带为 0)
dev = [(10^(Rp/20)-1)/(10^(Rp/20)+1), 10^(-As/20)]; % 计算通带、阻带的容差
[Ne, fo, mo, W] = remezord(fb, m, dev, Fs); % 确定等波纹设计所需参数
hn = remez(Ne, fo, mo, W); % 设计 FIR 滤波器
Hw = abs(fft(hn, 1024)); % 计算滤波器的幅频特性
yet = fftfilt(hn, xt, N); % 调用快速卷积函数对 xt 滤波
% 等波纹法设计结果绘图
figure(2); % 新建图形窗口 2
subplot(2,1,1);
myplot(hn, 1); % 绘制滤波器幅频特性
title('(c) 低通滤波器幅频特性(等波纹法)');
subplot(2,1,2);
yt = 'y_e(t)';
tplot(yet, T, yt); % 绘制滤波后信号时域波形
title('(d) 滤除噪声后的信号波形(等波纹法)');
2.2 信号产生函数 xtg.m
function xt = xtg(N)
% 实验五信号生成函数:生成含加性高频噪声的单频调幅信号
% 输入:N - 信号长度
% 输出:xt - 含噪声的单频调幅信号
% 采样频率 Fs = 1000 Hz,载波频率 fc = Fs/10 = 100 Hz,调制信号频率 f0 = fc/10 = 10 Hz
Fs = 1000; % 采样频率(单位:Hz)
T = 1/Fs; % 采样周期(单位:s)
Tp = N*T; % 信号总时长(单位:s)
t = 0:T:(N-1)*T; % 时间序列
% 生成单频调幅信号
fc = Fs/10; % 载波频率(单位:Hz)
f0 = fc/10; % 调制信号频率(单位:Hz)
mt = cos(2*pi*f0*t);% 单频正弦调制信号
ct = cos(2*pi*fc*t);% 正弦载波信号
xt = mt .* ct; % 相乘得到单频调幅信号
% 生成高频噪声并叠加至调幅信号
nt = 2*rand(1, N) - 1; % 生成 [-1,1] 范围内的随机噪声
% 设计高通滤波器以滤除噪声中的低频成分,生成高频噪声
fp_noise = 150; % 噪声高通滤波器通带截止频率(单位:Hz)
fs_noise = 200; % 噪声高通滤波器阻带截止频率(单位:Hz)
Rp_noise = 0.1; % 噪声滤波器通带最大衰减(单位:dB)
As_noise = 70; % 噪声滤波器阻带最小衰减(单位:dB)
fb_noise = [fp_noise, fs_noise]; % 噪声滤波器频率边界
m_noise = [0, 1]; % 噪声滤波器理想幅度(低频阻带为 0,高频通带为 1)
dev_noise = [10^(-As_noise/20), (10^(Rp_noise/20)-1)/(10^(Rp_noise/20)+1)]; % 噪声滤波器容差
[n_noise, fo_noise, mo_noise, W_noise] = remezord(fb_noise, m_noise, dev_noise, Fs); % 确定噪声滤波器参数
hn_noise = remez(n_noise, fo_noise, mo_noise, W_noise); % 设计高通滤波器
yt_noise = filter(hn_noise, 1, 10*nt); % 滤除噪声低频成分,放大噪声幅度
xt = xt + yt_noise; % 信号叠加噪声
% 绘制信号与频谱
fst = fft(xt, N); % 信号频谱(N 点 FFT)
k = 0:N-1; % 频率点索引
f = k/Tp; % 频率序列(单位:Hz)
subplot(3,1,1);
plot(t, xt);
grid on;
xlabel('t/s');
ylabel('x(t)');
axis([0, Tp/5, min(xt), max(xt)]);
title('(c) 信号加噪声波形');
subplot(3,1,2);
plot(f, abs(fst)/max(abs(fst)));
grid on;
title('(d) 信号加噪声的频谱');
axis([0, Fs/2, 0, 1.2]);
xlabel('f/Hz');
ylabel('归一化幅度');
2.3 时域波形绘制函数 tplot.m
function tplot(xn, T, yn)
% 时域波形绘制函数
% 输入:xn - 时域信号序列,T - 采样周期,yn - 信号标签
n = 0:length(xn)-1; % 信号索引序列
t = n*T; % 时间序列
plot(t, xn);
xlabel('t/s');
ylabel(yn);
axis([0, 0.5, min(xn), 1.2*max(xn)]); % 限定时间范围为 [0,0.5]s,幅度范围自适应
2.4 幅频特性(损耗函数)绘制函数 myplot.m
function myplot(B, A)
% 滤波器损耗函数(幅频特性)绘制函数
% 输入:B - 滤波器分子系数(FIR 滤波器仅需分子系数),A - 滤波器分母系数(FIR 滤波器为 1)
[H, W] = freqz(B, A, 1000); % 计算 1000 点频响
m = abs(H); % 幅频特性
% 绘制损耗函数(20log10 归一化幅度)
plot(W/pi*500, 20*log10(m/max(m)));
grid on;
xlabel('f/Hz');
ylabel('幅度(dB)');
axis([0, 500, -80, 10]); % 限定频率范围 [0,500]Hz,幅度范围 [-80,10]dB
title('损耗函数曲线');
代码修正说明
感谢用户@小白非常同学指出原代码中“tplot(ywt, T, yt);”的表述问题:该语句对应等波纹法的输出信号 yet,原文已修正为 tplot(yet, T, yt),实验结果图不受影响。此外,为避免学习者因不明确代码分段运行方式导致错误,在主程序中添加 figure(1) 与 figure(2) 以区分两种设计方法的绘图窗口,学习者也可通过调整 axis 函数参数获取更合适的信号显示效果。
五、实验结果截图(含分析)
1. 实验结果概述
- 窗函数法(Blackman 窗)设计的滤波器长度
N
b
=
184
N_b = 184
Nb=184,其损耗函数与滤波输出
y
w
(
n
T
)
y_w(nT)
yw(nT) 分别如图所示。

- 等波纹最佳逼近法设计的滤波器长度
N
e
=
83
N_e = 83
Ne=83,其损耗函数与滤波输出
y
e
(
n
T
)
y_e(nT)
ye(nT) 分别如图所示。

2. 结果分析
- 滤波效果:两种设计方法均能有效从含噪声信号中提取单频调幅信号,滤波后信号的高频噪声成分被显著抑制,时域波形平稳性明显提升。
- 阶数与资源对比:在相同技术指标下,等波纹最佳逼近法设计的滤波器阶数(83 阶)远低于窗函数法(184 阶)。阶数降低直接减少:
- 滤波实现的运算量;
- 信号滤波时延;
- 硬件资源(如 FPGA 中的乘法器、寄存器)消耗。
- 时延差异:从实验结果图的时域波形可直观观察到,等波纹法滤波输出的时延小于窗函数法,更适合对实时性要求较高的场景。
六、思考题
(1)窗函数法设计线性相位低通滤波器的步骤
已知通带截止频率、阻带截止频率及阻带最小衰减,窗函数法设计线性相位低通滤波器的步骤如下:
- 确定滤波器技术指标:明确通带截止频率 f p f_p fp、阻带截止频率 f s f_s fs、通带最大衰减 R p R_p Rp、阻带最小衰减 A s A_s As 及采样频率 F s F_s Fs。
- 频率换算:将模拟频率转换为数字频率,公式为 ω p = 2 π f p T \omega_p = 2\pi f_p T ωp=2πfpT、 ω s = 2 π f s T \omega_s = 2\pi f_s T ωs=2πfsT(其中 T = 1 / F s T = 1/F_s T=1/Fs)。
- 选择窗函数:根据阻带最小衰减 A s A_s As 选择合适窗函数(如 A s ≥ 60 dB A_s \geq 60 \, \text{dB} As≥60dB 可选 Blackman 窗, A s ≥ 40 dB A_s \geq 40 \, \text{dB} As≥40dB 可选 Hamming 窗)。
- 计算窗长:根据过渡带宽度 B = ω s − ω p B = \omega_s - \omega_p B=ωs−ωp 与窗函数类型计算窗长 N N N(如 Blackman 窗的窗长公式为 N = ⌈ 11 π / B ⌉ N = \lceil 11\pi / B \rceil N=⌈11π/B⌉, ⌈ ⋅ ⌉ \lceil \cdot \rceil ⌈⋅⌉ 表示向上取整)。
- 设计滤波器:调用 MATLAB 函数
fir1生成滤波器系数,格式为 h n = fir1 ( N − 1 , ω c / π , 窗函数 ) hn = \text{fir1}(N-1, \omega_c / \pi, 窗函数) hn=fir1(N−1,ωc/π,窗函数)(其中 ω c = ( ω p + ω s ) / 2 \omega_c = (\omega_p + \omega_s)/2 ωc=(ωp+ωs)/2 为理想低通滤波器的截止数字频率)。 - 验证指标:通过
freqz或myplot函数分析滤波器频响,若不满足指标则调整窗函数类型或窗长,重复步骤 4-5。
(2)理想带通滤波器截止频率的计算
已知带通滤波器的通带上下截止数字频率为 ω p l \omega_{pl} ωpl(通带下限)、 ω p u \omega_{pu} ωpu(通带上限),阻带上下截止数字频率为 ω s l \omega_{sl} ωsl(阻带下限)、 ω s u \omega_{su} ωsu(阻带上限),则理想带通滤波器的截止频率计算如下:
- 下截止频率 ω c l = ( ω p l + ω s l ) / 2 \omega_{cl} = (\omega_{pl} + \omega_{sl}) / 2 ωcl=(ωpl+ωsl)/2
- 上截止频率 ω c u = ( ω p u + ω s u ) / 2 \omega_{cu} = (\omega_{pu} + \omega_{su}) / 2 ωcu=(ωpu+ωsu)/2
计算逻辑:理想带通滤波器的截止频率需位于“通带与阻带的中间位置”,以确保过渡带宽度均匀,满足滤波指标。
(3)等波纹法滤波器阶数更低的原因
在相同技术指标下,等波纹最佳逼近法设计的滤波器阶数更低,原因如下:
- 窗函数法的资源浪费:窗函数法设计的滤波器若在阻带截止频率附近刚好满足衰减指标,离开该频率后阻带衰减会出现“富裕量”,导致硬件资源与运算资源浪费。
- 窗函数的指标限制:典型窗函数(如 Hamming、Blackman 窗)的通带最大衰减与阻带最小衰减为固定值,且无法分别独立控制,设计时需按更严格的窗函数指标匹配实验要求(如本实验需 A s = 60 dB A_s = 60 \, \text{dB} As=60dB,但 Blackman 窗的实际阻带衰减达 74 dB 74 \, \text{dB} 74dB),进一步增加阶数。
- 等波纹法的优化特性:等波纹最佳逼近法通过“切比雪夫逼近理论”使滤波器的通带与阻带均呈等波纹特性,通带最大衰减与阻带最小衰减可分别独立控制,指标均匀分布无富裕量,因此在满足相同指标时阶数显著更低。
via:
-
【数字信号处理】FIR 滤波器基础理论_fir 滤波器原理-优快云 博客
https://blog.youkuaiyun.com/m0_46612488/article/details/110127445 -
数字信号处理 (DSP) 实验——FIR 数字滤波器设计与仿真_如果给定通带截止频率和阻带截止频率以及阻带最小衰减,如何用窗函数法设计线性相-优快云 博客
https://blog.youkuaiyun.com/Insincerity/article/details/115647100 -
数字信号处理——FIR 滤波器设计_fir 滤波器四种类型-优快云 博客
https://blog.youkuaiyun.com/k331922164/article/details/117536723 -
数字信号处理:FIR 数字滤波器设计及软件实现_等波纹设计法绘图-优快云 博客…
https://blog.youkuaiyun.com/weixin_44026026/article/details/106507318 -
数字信号处理第五次试验:FIR 数字滤波器设计与软件实现-优快云 博客
https://blog.youkuaiyun.com/sjx3161/article/details/124247066 -
数字滤波器设计完全指南:从理论推导到 MATLAB/Python 实战—手把手实现 IIR/FIR、巴特沃斯、双二阶与陷波滤波器,附代码与避坑技巧 - 知乎
https://zhuanlan.zhihu.com/p/24342046101 -
基于 Matlab 的 FIR 滤波器设计与实现 - sunev - 博客园
https://www.cnblogs.com/sunev/archive/2011/11/23/2260579.html -
基于 Matlab 中 FDATool 工具箱的滤波器设计及相关文件的生成 - sunev - 博客园
https://www.cnblogs.com/sunev/archive/2011/11/22/2258426.html





















 1934
1934

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








