概率谬误 | 理解、识别及避免

注：本文为 “概率谬误” 相关合辑。
略作重排，未整理去重。
如有内容异常，请看原文。

---

概率的谬误，概率的概率，概率的哲学

原创 Ariel History Lab 历史实验室

2023 年 01 月 31 日 18:57 北京

在 1913 年某一天的摩纳哥蒙特卡洛赌场，一个众人围观的轮盘中，小球已经第 26 次停在了黑色。若是这个轮盘没有被动手脚，发生这样的事件的概率只有（18/37）的 26 次方——1.4 亿分之一！现场的人们都愈加高声地喊着“红色！红色！”——但他们已经为此输了上百万法郎。

两个看似冲突的想法让大部分人无法一时间做出合理的判断：

1.直觉上讲，已经连续这么多次转到黑色了，下一次还是黑色的概率也太太太小了，似乎总“该”是红色了！

2.可是细想，我们其实心里又都知道每一次转盘的结果应该是独立的——下一次无论是黑色还是红色概率都应该是一样的。

大量实验证明，我们绝大部分人很轻易地就会倾向于前一个想法。然而实际上，只要事件是独立的，概率就永远不会变。这就是赌徒谬误（Gambler’s Fallacy）：当现实中一个独立事件的发生频次高过了其既定概率时，我们会倾向于认为这个事件在之后发生的频次会降低（以**“凑出”概率**），反之亦然。

赌徒谬误不止会对预测未来造成偏差，同样也常常出现在对过去的推测中。当我们听说一个小概率事件发生时，会自然猜想已经过去了不少轮次（才终于发生这一次事件）。比如，当看到有人中了彩票，我们一般会认为这个人平时就有买彩票的习惯。

那么，这样的思维偏差究竟为什么会出现呢？

首要原因就是概率（Probability）这个概念本身和现实有脱离。我们对于概率的一种基本解释是：当轮次的数量趋近于无穷时，某个事件发生的频率就会趋近于该事件的概率。 假设硬币完全公正，当掷硬币的次数趋近于极限时，这一面朝上的频率就趋近于 50%。

这样一来，只有在我们能观察无数次的情况下，概率才能作为一个频率的准确数值——然而在现实中并不存在无穷大的样本。只要是在有限轮次当中，事件发生的频率就不是确定的——但概率却是一个精确数值，不能等同于频率。也因此，概率是不具有决定性的预测能力的。现实中，我们也就没有办法根据概率预测到下一轮次中会发生什么。

我们很容易高估样本对概率的代表性（Representative Heuristic）。然而，当样本数量有限时，既定概率和现实频率之间是无法划等号的，我们也是无法通过“凑出”概率来进行预测的。

我们也可以反过来论述。假设概率真的在任意大的样本中都代表了频率的准确数值，那么按理说，无论进行到多少轮次，事件发生的频率都应该是确定的。还是假设掷硬币，光是任意一个奇数轮次这样的论断都不可能成立（无法做到一半正面朝上半背面朝上）。我们根据现实中的证据也能接受这一点。

不过，就算是知道了这个误区的存在，我们的问题也还没完全被解决。因为即使样本数量有限时频率不是由概率决定的一个精准数字，我们至少也可以说：样本越大，现实频率与既定概率相等的概率更大（没错——"频率等于概率"的概率！）。

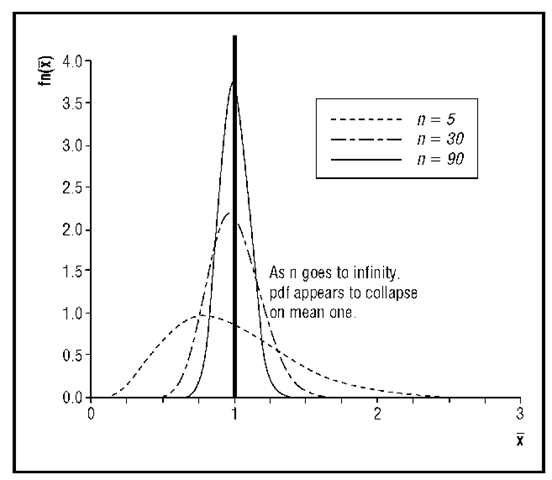
正如：掷硬币的次数越多，正面朝上的频率等于 50%的概率越大；同时掷两个骰子，次数越多，两个骰子之和等于 7 的概率就越大。回到最开始的例子：转轮盘的次数越多，序列里恰好一半红一半黑的概率不就是会越大，连续出现黑色的概率不就是会越来越小吗？

可实际上，无论是连续 27 次黑色，还是连续 26 次黑色+最后一次红色——甚至是任意一个特定的 27 次红黑序列——发生的概率都是一样的，都是（18/37）的 26 次方——1.4 亿分之一（轮盘一共 27 格，只有一格是绿色，占 1/37，因此红黑各是 18/37）！那么既然这样，怎么还会存在特定的组合概率更小呢？

上面这两件事看似彼此冲突，实际上说的不是一回事。出现这个偏差的源头就在于我们混淆了组合（Combination）和序列（Sequence）。

还是拿掷两个骰子来举例子：两个骰子之和是 7 这种组合方式的概率是最大的——然而这种组合里面包括了 6 种不同的序列。两个不同的骰子掷出来的序列一共有 6*6=36 种可能性，每一个序列被掷出来的概率都是一样的——都是 1/36。当我们说某一种组合出现的概率大时，实际上是因为这种组合里面包含的序列个数多。

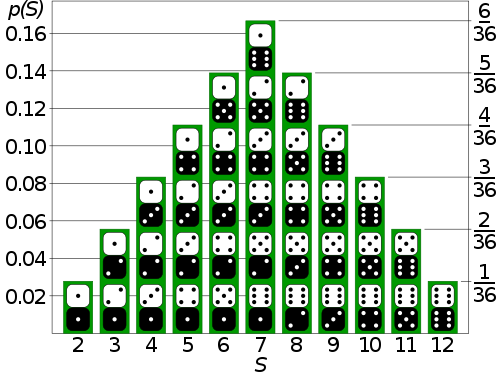
这样分析对掷硬币也适用。比如，当掷四枚硬币时，一共有 2 的 4 次方——16 种可能的序列。其中两正两反的组合包含的序列一共有 6 种，一正三反和一反三正的序列则各有 4 种。

同样，转轮盘的次数越多，连续转到黑色的组合概率就越小，其他组合的概率就越大；但是，每一个序列本身的概率并不会变——而我们在对付的恰恰是一个序列，而不是包含了多个序列的组合。

这和物理学中熵（Entropy）的概念非常相似。熵，通俗来解释，就是某一种宏观状态（Macro-States）对应着的微观状态（Micro-States）的个数（严格来说，直接对应着的是对数）。这里宏观状态就对应着我们前面所提到的组合，而微观排列则对应着序列。当我们说某一个宏观状态的熵更高时，实际上就是指能形成这种宏观状态的微观状态的个数更多。比如，具有相同位置和动量分布但排列不同的气体粒子体系都能够使气体宏观显示出相同的温度、压力、体积。

根据这个定义，我们能够很清晰地看出，熵更高的宏观状态正是概率更高的状态——因为更多种微观状态都会对应到这一宏观状态，而每一个微观状态本身的概率又是相等的。从这里出发，我们也就能够相对直观地理解为什么熵增会是是宇宙最基本的特质之一——一旦概率低的状态被破坏变成概率高的状态，就很难再回到从前了。

这和我们轮盘的例子的不同之处就在于：我们在轮盘中关注的是序列，既然每一个序列的概率都是相等的，我们也就没有必要认为某一个序列比另一个序列更可能出现了；然而，在熵的例子中，我们关注的却是宏观状态，其本身就是组合，因此我们也就可以正当地认为某一种更“容易”出现了。

那么，既然我们已经分析了这么多造成赌徒谬误的思维偏差，若是真遇到了轮赌盘连续 26 次黑色的时候，我们到底应该怎么赌下一局才能尽可能提高胜算呢?

与赌徒谬误正相反——此时理性的做法反而是继续猜黑色。在有关贝叶斯定理的文章中，我们曾经提到过，千万不要把任何假设当作百分之百正确或错误。

在刚刚我们所有的论述中，我们一直都假设了游戏是公正的，概率是既定的。然而实际上，这一点在实际中往往并不成立。当转盘已经连续转了 26 次时，我们不免要怀疑，这个轮盘本身转到黑色和红色的概率真的是一样大的吗？

等等，我们刚刚不是才说每一个序列出现的概率都一样大吗？既然如此为什么还要怀疑这个序列的出现是有问题的？注意，这和我们刚刚并不是同一个问题：当看到连续的黑色时候我们之所以会怀疑，并不是因为这个序列出现的概率比别的序列小，而是说这个序列的出现会使得的“这个轮盘是偏向黑色的”这个假设的概率增大。

这时我们也就不得不提到对于概率本质的另一种解释——置信度（Degree of Belief）。上文我们提到，对于既定概率，我们不妨理解成在无穷次轮次当中事件发生次数的频率所趋近的值。

然而在现实生活中，概率往往不是一个我们预先知道的准确数值，而是在一次一次的反复测试中通过我们不断更新信息而被变化的数字——也就是我们对于此时会发生的可能性的把握。而更新这个把握的系统数学方法，就是通过贝叶斯定理（Bayes Theorem）。简单来说，贝叶斯定理是在新信息出现时更新旧假设成立概率的系统数学方法，可以从概率的基本运算原理推出来。

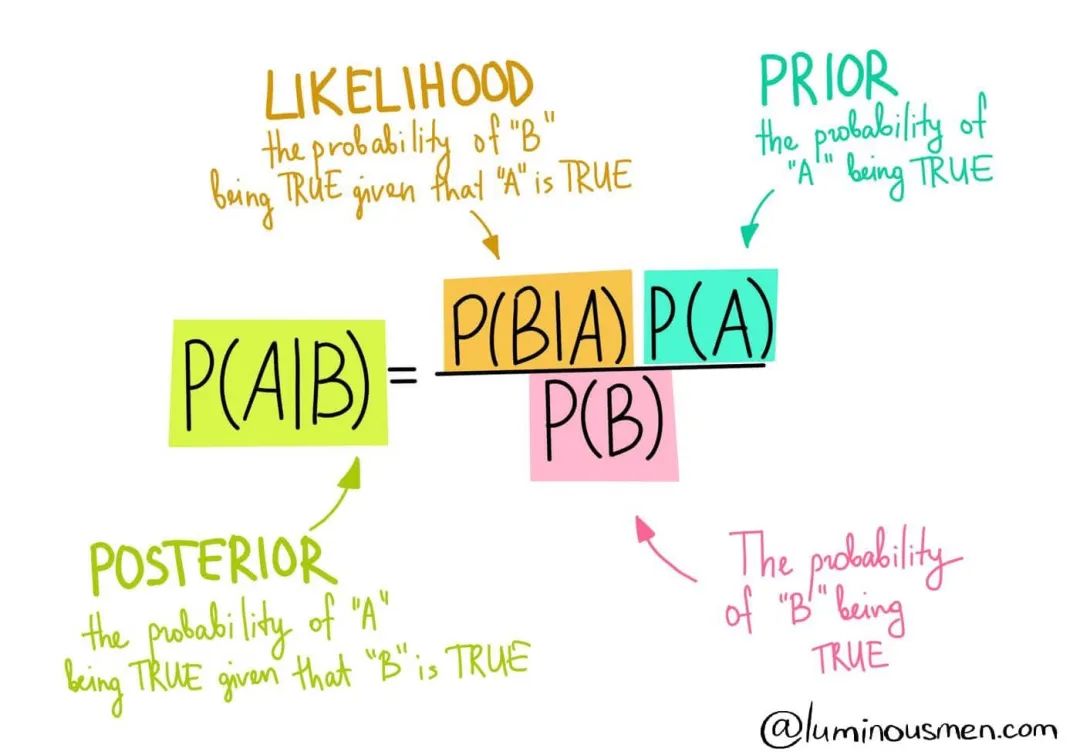
若是我们本身保持一个怀疑的态度，不笃定这个轮赌盘没有被动过手脚，随着黑色的次数一次次增加，我们不免要对“这个轮盘是偏向黑色的”这个假设的概率进行更新。若是最开始我们假定这个假设为真的概率只有 1%，那么第 26 次连续出现黑色时，可能这个概率就会增长到 40%（即使我们还没有使用贝叶斯定理计算得到准确数据，想必概率会增高这一点也非常直观了）。这样一来，我们反而有了一定根据猜测下一次结果还是黑色的——因为轮盘可能并不公正（比如，黑色方块的下方可能有磁铁，能够吸引小铁球）。

不管是对于样本代表性的误判还是对于序列和组合的混淆，有趣的地方在于，这些都一定程度上指向了：也许正是人类对于概率的认知使得我们无法做出更好的判断。

在一个人与老鼠的对比实验中，实验设置分别有一个绿灯一个红灯，每轮都会有其中一个灯亮起来。绿灯亮起来的概率是 70%，红灯亮起来的概率是 30%。若是被试者能够在灯亮起来之前猜对，就会获得奖励。

老鼠被试者们在几轮重复后很快就意识到了选择绿色更占优势，于是就只选择绿色——最终答对的果然就在 70%左右。而相反，人类被试者们却几乎没有一个这么做，而是反复尝试去“凑”概率——结果反而连 60%都不到。

起码在这种情况下，像老鼠这样对概率没有抽象认知、不去主动“凑”概率的方法似乎是更占优势的（又或者是：老鼠不仅非常了解概率，还比人还多想了一层——它们也许正在嘲笑人类的愚蠢呢）。

然而，想要改变人类这样的思维习惯非常难：曾经就有人通过对比实验证明了，在测试前得到有关概率谬误警醒的实验组和没有得到警醒的对照组在相同的情景下犯赌徒谬误的比例竟然相差无几！

为什么我们会这么容易在知道一点概率后就上概率的当呢？和都是源于概率在现实中这个很“尴尬”的角色：

一方面，对于现实中我们所有能观测到的事件（已经发生的事情），发生的概率都只能是 1——因为我们能够只能够观测到存在性的唯一现实（要么存在要么不存在），不能直接观测到概率性（存在的可能性有多大）。

另一方面，人类似乎又具有对未来的不同可能性的很强的脑内模拟能力。我们很轻易就能够接受（大众文化中）“多元宇宙”的概念，对于一个事件发生与否同时进行模拟（尽管现实只可能是其中之一）——我们竟然能够接受一个像概率这样的抽象概念。可同时，我们也还是无法知道究竟概率性的哪一种结果会在现实中会发生。

于是就出现了这样一个局面：概率只对于还未发生的事情有意义，但我们又无法直接看到其作用。 当我们提到事件的概率时，实际上谈的是一个在现实当中并不被显现出来的抽象数字。

于是到这里，我们不得不讨论：概率到底是什么？

在前文中，我们提到了关于概率的两种解释：一种是样本趋近于无穷大时事件发生的频率所趋近的值，另一种是我们对于事件发生的可能性的把握。不过要是细想，这两种解释都有点奇怪。

对于第一种概率“客观”解释，我们不妨用直觉分析一下：事件发生的频率显然不一定趋近于概率吧？还是拿硬币举例：只要连续都是正面还是可能的，我们就没有办法说趋近是必然的。而是否轮次越多在概率附近的抖动就越小呢？我们似乎很轻易就能想出来反例。那既然**概率在现实当中并不能被直接验证，所谓“客观”概率究竟是如何被定下来的呢？**大概说到底还是一个独立于概率本身的猜测吧（比如硬币 50%的概率就是根据其对称的形状猜出来的）！

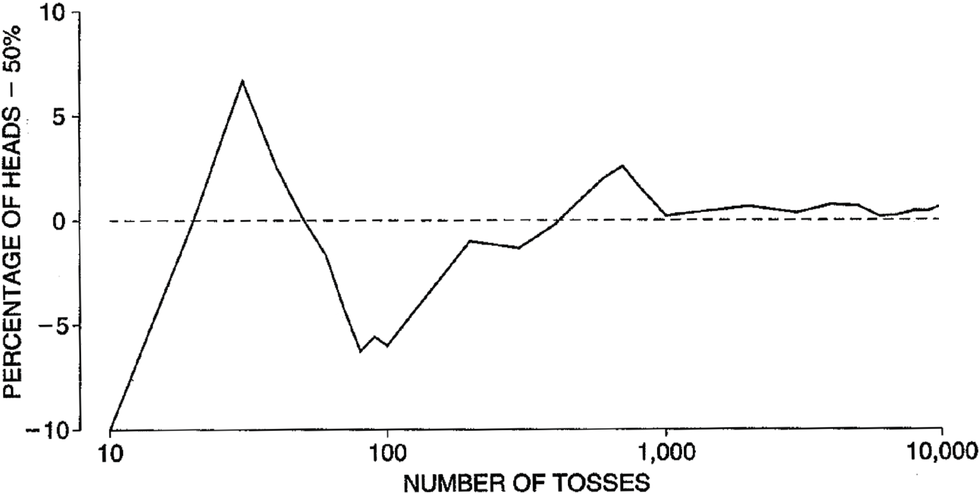
而对于第二种概率贝叶斯式的“主观”解释，概率是什么就更说不清楚了。我们似乎很难接受现实中的概率本身就是主观的——只是因为我们的信息不完整才无奈将概率理解成主观的。

我们似乎无法找到任何一种概率的解释能够直接与现实相对应，说不清楚概率是什么；可与此同时，我们又好像能够很天然直观地理解概率要怎么样用和理解——这难道不是非常不可思议吗！？

最后感谢感谢读到这里的各位！我们在这篇文章中一起探讨了赌徒谬误和其产生的两个根源（对于样本概率代表性的高估和对组合和序列的混淆），最后也深入到了人类对于概率的认知和一些有关概率的哲思。敬请期待下次更新～

History Lab 历史实验室

We reach back to antiquity, and forward to the stars. ——好奇心与头脑的连接，知识与思想的融会贯通！

内容包括但不限于自然科学、哲学、社会科学、数学。

References：

Belief in the Law of Small Numbers, Amos Tversky, Daniel Kahneman
Gambler’s Fallacy, Wikipedia
Law of Large Numbers, Wikipedia
Probability, Wikipedia
Sex, Death, and the Meaning of Life, Richard Dawkins
The Feynman Lectures on Physics, Richard Feynman
The Left Hemisphere’s Role in Hypothesis Formation, George Wolford, Michael B. Miller, and Michael Gazzaniga

作者 Ariel

审阅 Thea Linda

---

揭秘基础率谬误：为何我们总是被细节迷惑，忽略了真实概率？

原创 诊断科学 诊断科学 2024 年 04 月 03 日 19:00 广东

探索基础率谬误如何在日常决策中误导我们，特别是在体外诊断试剂行业和医学检验领域，本文将揭示这种认知偏误背后的心理学原理，并提供实用策略以避免其影响，确保更准确的判断和决策。

01 什么是基础率谬误？

基础率谬误（Base Rate Fallacy）是一种认知偏误，当一个人过分重视案例特定的细节，并忽略了适用于整个人群的关键概率信息时，就会误判结果。这种关键的概率是结果在人群中发生的基础率（Base Rate）。

本质上，一个人因为被特定细节所困扰而误解了一个结果，忽视了总体的发生频率。人们倾向于使用相似性而非统计可能性（Statistical Likelihoods）来进行预测。因此，这种偏误也被称为基础率忽视（Base Rate Neglect）。

但为什么会这样呢？这是我们大脑对故事而非数字、对引人入胜的细节而非冷酷的统计数据的偏好的故事。让我们来看一个实际例子！

想象你在本地公园，注意到有人在使用望远镜，并在笔记本上做详细记录。他们穿着休闲，但有一个带有天文符号的徽章。基于这些特定细节，你得出结论，这个人是天体物理学家或专业天文学家。然而，这个假设可能是基础率谬误的一个例子。

虽然设备和徽章暗示了一个罕见和具体的天文学职业，但在一般人群中遇到专业天文学家的基础率极低。这个人可能是业余天文爱好者或准备课程的老师。通过专注于特定可观察的细节并忽视基础率，你的结论可能远离真相。

在这篇文章中，我们将探讨基础率谬误的概念，为什么会发生，以及这种认知偏误如何影响我们的日常决策。最后，我将包括一个解决医疗测试概率的基础率谬误的实际例子。

02 理解基础率谬误为什么会发生

我们为什么会陷入这种谬误？答案在于我们的认知结构。我们的大脑被编程为喜欢故事和特定细节；它们在情感上吸引我们，并且比抽象概率更容易回忆。虽然这种偏好通常很有帮助，但它可能导致我们忽视应该指导我们决策的统计现实。

让我们定义“基础率”。想象它是我们应该用来权衡任何新信息的概率背景。例如，如果只有 1/1000 的人有一种罕见的疾病，那就是基础率。简单，对吧？然而，面对具体而生动的细节时，我们的大脑往往会将这个关键的统计背景置于次要地位。

基础率谬误展示了一个常见的认知挑战：将特定情境细节与更广泛、更一般化的数据整合起来。当只有一般的基础率信息可用时，人们通常依赖它，但在特定和一般信息都存在时，人们就会挣扎。

我们的大脑更喜欢情境细节而非统计概率！在这个意义上，基础率谬误与联结谬误（Conjunction Fallacy）相似。

03 基础率谬误的影响

这种认知怪癖可以影响我们在各种情境中的判断，从医疗诊断到财务预测、法律决策和日常生活中的选择。基础率谬误可以使我们误入歧途，导致误判和低效率，因为它扭曲了我们对风险和可能性的感知。

例如，在社交互动中，基础率谬误可能导致我们忽视某人在类似过去情境中的行为（基础率），导致我们基于即时、可观察的特质形成判断。这种方法可能过于简化复杂的人类行为。

在财务环境中，投资者可能会基于近期事件而非长期趋势（基础率）做出决策。

在法律系统中，基础率谬误可以显著影响法庭决策。例如，法官和陪审团可能过分关注特定案件或证词的引人入胜的细节，而忽视更广泛的统计数据，如犯罪率或某些事件发生的可能性。这种不平衡可能导致证据的误解和可能的不公正判决。

也许你听说过大多数感染 COVID 的人已经接种了针对该疾病的疫苗？如果这让你认为疫苗无效，欢迎来到另一个基础率谬误的例子！

在所有这些例子中，你需要正确平衡特定案例和一般信息，以获得对复杂情境更准确的理解。这种方法帮助你避免陷入基础率谬误的陷阱。

在以下实际例子中，你将看到医疗专业人员如何通过过分关注个别测试结果而忽视更广泛的统计数据而陷入这个陷阱。我将向你展示如何找到正确答案！

04 基础率谬误实际例子

考虑医疗测试中常见的基础率谬误。阳性测试结果真正意味着什么？

假设一位患者对严重疾病进行了阳性测试结果。你能成功地合并特定案例和基础率信息，找到正确答案吗？

以下是细节：

► 特定案例：使用 95%准确的测试得出阳性测试结果。95%的时间，测试在一个人患有疾病时产生阳性结果。

► 基础率：1/1000 的人有这种状况。

鉴于这些信息，阳性测试结果的患者患有该病的概率是多少？

最常见的答案是 95%，鉴于测试的高准确性，这听起来是合理的。

然而，正确答案约为 2%。如果这是一个大惊喜，那是因为你成为了基础率谬误的受害者！

具体来说，你没有将疾病在人群中发生的基础率（概率为 0.001）纳入考虑。

让我们解决这个问题！这里是一个简单的 Excel 工作表，可以计算答案并允许你更改参数：基础率谬误计算。

现在，我将带你通过计算，结合基础率。

05 解决基础率谬误

避免基础率谬误的关键是正确评估特定案例信息在人群整体概率背景下的情况。

对于医疗测试示例，测试在特定案例中非常准确（95%），但我们需要在医疗状况罕见的背景下解释这一点——基础率仅为 0.001。当整体可能性较低时，我们需要担心假阳性的作用。

要回答基础率谬误问题，请考虑以下内容：

我们知道，在人群中，有 0.001 的人有这种状况，所以 1 – 0.0001 = 0.999 的人没有。

此外，测试有 0.95 的真阳性率，意味着它有 1 – 0.95 = 0.05 的假阳性率。

现在，让我们将这些信息应用于 100 万人口中，以找到真阳性和假阳性的数量。

1 案例和真阳性

让我们以 1,000,000 人口为例，乘以状况的基础率，以找到病例数量：1,000,000 × 0.001 = 1,000。

现在，我们将我们的 1000 个病例乘以测试的准确率，以找到真阳性数量：1000 × 0.95 = 950。

我们预计在我们的人口中将获得 950 个真阳性。

2 非案例和假阳性

现在，我们将使用其基础率找到非病例的数量：1,000,000 × 0.999 = 999,000。

999,000 人没有这种状况，但当他们进行测试时，存在假阳性概率。让我们使用这个来计算假阳性数量：999,000 × 0.05 = 49,950。

3 把他们放在一起

大多数患有该病的 1,000 人获得了真阳性测试结果（950）。然而，对于那些没有该病的人来说，有惊人的 49,950 人获得了假阳性结果！虽然假阳性率很低（0.05），但这么多人没有该病，以至于测试产生的假阳性比真阳性多得多。

哇！假阳性比真阳性多得多，这解释了为什么基础率谬误给我们一个极其偏见的想法！

因此，总共 50,900 个阳性中只有 950 个是真阳性：950 / 50,900 = 1.87%。

在示例中，我们的计算表明，阳性测试结果实际患有疾病的概率约为 1.87%。低基础率（1/1000）极大地影响了阳性结果患有该病的可能性，即使测试准确度为 95%。

基础率谬误导致大多数人完全误判了这个测试的阳性结果的含义，因为这种疾病的罕见性。

几点注意事项。如果你改变了人口的规模，答案仍然相同。有一个使用贝叶斯概率（Bayesian Probabilities）的更复杂解决方案，但结果相同。这种方法更好地强调了基础率如何影响真阳性与假阳性的比例。

06 避免基础率谬误！

总之，基础率谬误是一种普遍存在的认知偏误，对我们的决策产生重大影响。正如我们所看到的，当我们过分重视特定情境的细节，而忽视事件发生在人群中的一般概率或基础率时，就会发生这种谬误。

理解基础率谬误对于做出更明智、更理性的决策至关重要。记住，下次你面临决策或形成观点时，暂停并思考基础率。尝试正确结合特定和一般信息。

参考文献

[1] Kahneman & Tversky, On the psychology of prediction. Psychological review, 1973, 80, 237-257.

---

7 个基本逻辑概率谬误

万维钢 不学无数 2015 年 12 月 07 日 18:01

几个基本的逻辑概率谬误：

（1）因果颠倒：比如：不少人用"女人祸水论"来解释官员腐败原因。然而,这种观点在逻辑上显然属于因果颠倒。官员才是“因”，而女人只是“果”而已。

（2）以时间先后断因果：A 事件发生在 B 事件之前，但是 A 事件并不一定是 B 事件发生的原因，故：你当然不能说公鸡打鸣是太阳升起的原因吧。

（3）随机事件：很多随机事件，发生就发生了，没有太大可供解读的意义。我们不能从这件事获得什么教训，不值得较真，甚至不值得采取行动。比如一个人卖彩票中奖了，结果他去分析各种“中奖经验”画出各种中奖曲线图试图再次中奖，我只能说：呵呵。

（4） 赌徒谬误：数学上独立的随机事件，这意味着下一把的结果和以前所有的结果都没有任何联系，已经发生了的事情不会影响将来。比如：你如果连输几把，那么下一把就应该会赢吗？要知道每次随机事件与前面是没有任何联系的哦。所以彩票每次买同一个号码的中奖概率都是一样的。同样：用“攒人品”或“败人品”来判断未来的事件的发展趋势从独立事件上来说也是不靠谱的。

（5）在没有规律的地方发现规律（马后炮逻辑）：事后，你只要你愿意忽略所有不符合你这个规律的数据，而强调符合这个规律的数据，就能发现规律。而且只要如果数据够多，我们可以找到任何我们想要的规律。典型的就是股票分析师（我妈妈每天都听他们的忽悠，乐此不疲）从那么多股票数据里面找出符合他们要求的规律数据当然不难，他们能真的找到股票运行规律吗？如果真找到规律他们还能让你知道吗？让他断言一下未来，行么？

（6）小数定理谬误：如果数据足够少，有些规律会自己跳出来，你甚至不相信都不行。比如： “巴西队的礼物”：只要巴西夺冠，下一届的冠军就将是主办大赛的东道主，除非巴西队自己将礼物收回。这一定律在 2006 年被破解。（到目前：巴西夺冠 5 次）

（7）大数定律与小数定律：大数定律是我们从统计数字中推测真相的理论基础。大数定律说如果统计样本足够大，那么事物出现的频率就能无限接近他的理论概率——也就是他的“本性”。而小数定律说如果样本不够大，那么他就表现为各种极端情况，而这些情况可以跟他的本性一点关系都没有。

比如：某人看到电视上飞机空难，很惨烈，这辈子就不敢乘飞机。

再比如：·一个只有二十人的乡村中学某年突然有两人考上清华，跟一个有两千人的中学每年都有两百人考上清华，完全没有可比性。

所以：我们才不能只凭自己的经验，哪怕加上家人和朋友的经验，去对事物做出判断。我们的经验非常有限。别看个例，看大规模统计。有的人听说两三个负面新闻就敢写文章把社会批得一文不值，这样的人非常无知。

我认为人人都应该学一些概率知识，它现在是公民必备知识。

现在的世界比过去复杂得多，其中有大量不确定性，是否理解概率，直接决定一个人的开化程度。

1. 随机：有些事情是无缘无故地发生的

这个思想对我们的世界观有颠覆的意义。

古人没有这个思想，认为一切事物都是有因果的，甚至可能都是有目的的。人们曾经认为世界像一个钟表一样精确地运行。但真实世界不是钟表，它充满不可控的偶然。

更严格地说，有些事情的发生，跟他之前发生的任何事情，都可以没有因果关系。不论我们做什么都不能让它一定发生，也不能让它一定不发生。

一个人考了好大学，人们会说这是他努力的结果；一个人事业成功，人们会说这是他努力工作的结果。可是如果一个人买彩票中了大奖，这又是为什么呢？

答案是没有任何原因，这完全是一个随机事件。总会有人买彩票中奖，而这一期彩票中奖，跟他是不是好人，他在之前各期买过多少彩票，他是否关注中奖号码的走势，没有任何关系。

若一个人总是买彩票，他中奖的概率会比别人大点吧？的确，他一生之中中一次奖的概率比那些只是偶然买一次彩票的人大。但是当他跟上千万个人一起面对一次开奖的时候，他不具备任何优势。他之前所有的努力，对他在这次开奖中的运气没有任何帮助。一个此前没有买过任何彩票的人，完全有可能，而且有同样大的可能，在某一次开奖中把最高奖金拿走。

中奖，既不是他个人努力的结果，也不是“上天”对他有所“垂青”；不中，也不等于任何人与他做对。这就是“随机”，你没有任何办法左右结果。

理解随机性，我们就知道很多事情发生就发生了，没有太大可供解读的意义。我们不能从这件事获得什么教训，不值得较真，甚至不值得采取行动。

· 再完美的交通工具也不可能百分百安全，我们会因为极小的事故概率不坐飞机吗？我们只需要确定事故概率比其他旅行方式小就可以了。甚至连这都不需要，只需要确定这个小概率事件我们能够容忍就可以了。

2. 赌徒谬误

假如你在赌场玩老虎机，一上来运气不太好，连输好几把。这时候你是否有种强烈的感觉，你很快该赢了？

买股票、期货、彩票都是一样。连续好几把上来就亏损的情况下，是不是觉得下一把挣钱的概率很大？

这完全是一种错觉。赌博完全是独立的随机事件，这意味着下一把的结果和以前所有的结果都没有任何联系，已经发生了的事情不会影响将来。

“大数定律”说，如果进行足够多的抽奖，那么各种不同结果出现的频率就会等于他们的概率。

人们常常错误地理解为，随机就意味着均匀。如果过去一段时间内发生的事情不均匀，人们就错误的以为未来的事情会尽量往“抹平”的方向走。如果连输几把，那么下一把就应该会赢。

但大数定律的工作机制不是和过去搞平衡，它的真实意思是说如果未来进行非常多次的抽奖，你输非常多次、赢非常多次，以至于他们此前的一点点差异就会变得微不足道。

· 有个笑话说一个人乘坐飞机时总带着一颗炸弹，他认为这样就不会被恐怖分子炸飞机了，因为一架飞机上有两颗炸弹的可能性非常小。

· 战场上士兵有个说法，如果战斗中炸弹在你身边爆炸，你应该迅速跳进那个弹坑，因为两颗炸弹不大可能打到同一个地方。

这都是不理解独立随机事件导致的。

3. 在没有规律的地方发现规律

理解了随机性和独立随机事件，我们可以得到一个结论：独立随机事件的发生是没有规律和不可预测的，这是一个非常重要的智慧。

彩票分析师，相信中奖号码存在走势，相信其中的规律，所以近期多次出现的组合可能会继续出现，或者按照这个趋势可以预测下一个号码。

但这里根本没有规律，是完全随机的现象，即便存在缺陷，也需要大量的开奖后才能发现，而且缺陷的结果也很简单，无非是某个特定号码出现的可能性略大一些，完全谈不上什么复杂规律。

明明没有规律，这些彩票分析师是怎么看出规律来的呢？也许他们不是故意骗人，而很可能他们真的相信自己找到了彩票的规律。

发现规律是人的本能。

春天过后是夏天，乌云压顶常下雨，大自然中很多事情的确是有规律的。我们的本能工作得如此之好，以至于我们在明明没有规律的地方也能找出规律来。人脑很擅长理解规律，但是很不擅长理解随机性。

在没有规律的地方发现规律是很容易的事情，只要你愿意忽略所有不符合你这个规律的数据。而且如果数据够多，我们可以找到任何我们想要的规律。

· 有人拿圣经做字符串游戏，声称这是圣经对后世的预言。问题是，这些预言可以完美的解释已经发生的事情，但在预测未发生的事情时就不好使了。关键是圣经中有很多很多字符，如果仔细寻找，尤其是借助计算机的话，总能找到任何想要的东西。

· 把圣经换成毛选也一样，你会发现毛选也早就预言了中国后世发生的所有大事。

未来是不可被精确预测的，这个世界也并不像钟表那样运行。

4. 小数定律

现在我们知道，数据足够多的话，人们可以找到任何自己想要的重要规律，只要他不在乎这些规律的严格性和自洽性。那么在数据足够少的情况下又会如何？

如果数据足够少，有些规律会自己跳出来，你甚至不相信都不行。

人们抱着游戏或者认真的态度总结了世界杯足球赛的各种“定律”。比如——

“巴西队的礼物”：只要巴西夺冠，下一届的冠军就将是主办大赛的东道主，除非巴西队自己将礼物收回。这一定律在 2006 年被破解。

“1982 轴心定律”：世界杯夺冠球队以 1982 年世界杯为中心呈对称分布，这个定律在 2006 年被破解。

5. 还有一些未被破解的定律，比如——

· 凡是获得联合会杯或美洲杯，就别想在下一届世界杯夺冠。

· 中国队的“王治郅定律”：只要王治郅参加季后赛，八一队必然得总冠军，以及“0:2”落后无人翻盘定律。

如果仔细研究这些定律，会发现不易破解的定律其实都有一定的道理。王治郅和八一队都很强，0:2 落后的确很难翻盘，而获得世界杯冠军是个非常不容易的事情，更别说同时获得联合会杯、美洲杯和世界杯。但不容易不等于不会发生，他们终究会被破解。

那些看似没有道理的神奇定律（正因为没道理，所以显得神奇），则大多数已经被破解。之所以神奇，是因为纯属巧合。世界杯总共才进行了 80 多年，20 多届。只要数据足够少，我们总能发现一些没有破解的规律。

如果数据少，随机现象可以看上去很不随机。甚至非常整齐，感觉好像真有规律一样。

问题的关键是，随机分布不等于均匀分布。要想均匀分布，必须要样本总数非常大的时候才有效。一旦不均匀，人们就认为其中必有缘故（阴谋论），而事实却是这可能只是偶然事件。

iPod 最早推出“随机播放”功能的时候，用户发现有些歌曲会被重复播放，他们据此认为播放根本不随机。苹果公司只好放弃真正的随机算法，用乔布斯本人的话说，就是改进以后的算法使播放“更不随机以至于让人感觉更随机”。

如果统计数据很少，就很容易出现特别不均匀的情况。这个现象被诺奖得主丹尼尔·卡尼曼戏称为“小数定律”。卡尼曼说，如果我们不理解小数定律，就不能真正理解大数定律。

大数定律是我们从统计数字中推测真相的理论基础。大数定律说如果统计样本足够大，那么事物出现的频率就能无限接近他的理论概率——也就是他的“本性”。而小数定律说如果样本不够大，那么他就表现为各种极端情况，而这些情况可以跟他的本性一点关系都没有。

· 一个只有二十人的乡村中学某年突然有两人考上清华，跟一个有两千人的中学每年都有两百人考上清华，完全没有可比性。

如果统计样本不够大，就什么也说明不了。

正因为如此，我们才不能只凭自己的经验，哪怕加上家人和朋友的经验，去对事物做出判断。我们的经验非常有限。别看个例，看大规模统计。有的人听说两三个负面新闻就敢写文章把社会批得一文不值，这样的人非常无知。

---

许兴华——揭秘常见的概率谬误：让我们避免陷入数学陷阱

原创 南宁许兴华 许兴华数学 2023 年 03 月 20 日 00:00 广西

概率论是现代生活中一个重要的数学工具，但有时候，我们对概率的理解和运用会出现一些误区。本文将为大家介绍一些常见的概率谬误，帮助大家在日常生活中更好地应用概率知识。

1.赌徒谬误（Gambler’s Fallacy）

赌徒谬误是指人们在面对独立随机事件时，错误地认为前面的结果会影响后面的结果。例如，在抛硬币游戏中，如果连续出现几次正面，有些人可能会认为接下来更有可能出现反面，以实现“平衡”。然而，实际上每次抛硬币都是独立的随机事件，前面的结果不会影响后面的结果。

2.忽略基本概率（Base Rate Fallacy）

忽略基本概率是指在估计一个事件发生的概率时，忽略了基本概率，只关注特定的信息。例如，在估计某人患上某种疾病的概率时，只关注这个人的年龄、性别等特征，而忽略了整个人群中患病的基本概率。

3.生日悖论（Birthday Paradox）

生日悖论是指在一个相对较小的人群中，至少有两个人生日相同的概率远高于我们的直觉预期。实际上，在一个包含 23 个人的群体中，至少有两个人生日相同的概率已经超过了 50%。这个悖论揭示了我们在直观判断概率时容易犯的错误。

4.确定性偏误（Certainty Effect）

确定性偏误是指人们在面对不确定性时，倾向于过高地估计确定性结果的概率。例如，在购买彩票时，很多人会认为自己中奖的概率很低，但实际上，如果购买足够多的彩票，中奖的概率就会显著提高。这种现象反映了我们对于不确定性的恐惧和对确定性结果的追求。

5.锚定效应（Anchoring Effect）

锚定效应是指在判断概率时，人们容易受到先前接触过的信息的影响。例如，在估计一件物品的价格时，我们可能会受到商家标注的原价或参考价的影响，从而对实际价格产生误判。同样，在估计事件发生的概率时，我们也可能受到之前的一些经验、新闻报道等信息的影响，而忽略了其他重要的因素。

6.可视化效应（Availability Heuristic）

可视化效应是指在判断概率时，人们容易受到容易回忆起来的信息的影响。由于新闻报道和社交媒体等信息渠道的传播效应，一些罕见但引人注目的事件（如空难、恐怖袭击等）容易给人留下深刻印象，从而导致我们高估这类事件的发生概率。

7.乌鸦效应（Conjunction Fallacy）

乌鸦效应是指在估计概率时，人们错误地认为多个特定条件同时发生的概率高于其中任意一个条件发生的概率。例如，在估计某人同时具备某种职业和某种特长的概率时，我们往往会高估这一概率，忽略了这两个条件本身的独立概率。

概率谬误无处不在，了解它们有助于我们在生活中更加理性地应对概率问题。通过学习和实践，我们可以避免陷入这些数学陷阱，更好地运用概率知识解决实际问题。希望本文能帮助大家提高对概率谬误的认识，让大家在面对概率问题时更加自信、明智。

---

朴素逻辑的 48 种典型认知漏洞

老谭说事儿 2025 年 06 月 18 日 14:31 湖南

最近看到了这份逻辑认知漏洞清单，深有所感，特转发如下：

一、基础推理缺陷

1．后此谬误（ Post Hoc Ergo Propter Hoc )：因事件 A 先于 B 发生，即认定 A 是 B 的原因（如"鸡鸣后太阳升起，故鸡鸣导致日出")

2．片面归因（ Texas Sharpshooter ):选择性聚焦支持结论的数据，忽视反例（如仅用 3 月数据证明气候变暖）

3．错误二分（ False Dilemma )：将复杂问题简化为非此即彼的选项（如"不用核能就只能烧煤")

4．循环论证（ Circular Reasoning )：结论本身已隐含在前提中（如"圣经无误，因为它是神的话语，而神说过圣经无误")

5．合成谬误（ Composition Fallacy )：认为局部特性必然适用于整体（如"每个球员都很强，所以球队一定夺冠")

6．分解谬误（ Division Fallacy )：将整体属性错误赋予局部（如"优秀团队中的成员必然优秀")

二、证据处理偏差

7．确认偏误（ Confirmation Bias )：主动寻找支持既有观点的证据，回避反面信息（如阴谋论者只关注"可疑"线索）

8．轶事证据优先（ Anecdotal Fallacy )：用个别案例替代系统研究（如"我爷爷抽烟活到 90 岁，证明吸烟无害")

9．诉诸无知（ Argument from Ignorance )：因无法证伪即认定真实（如"无法证明外星人不存在，所以它们存在")

10．数据误读（ Base Rate Neglect )：忽视基础概率导致的判断错误（如忽视罕见病发病率，因检测阳性直接恐慌）

11．幸存者偏差（ Survivo rship Bias )：仅分析成功样本而忽略失败者（如"二战战机弹孔分布"经典案例）

12．生态谬误（ Ecological Fallacy )：用群体数据推断个体行为（如"高犯罪率社区的居民都有犯罪倾向")

三、情感与权威干扰

13．诉诸情感（ Appeal to Emotion )：用情绪操控替代逻辑论证（如"不支持环保政策就是不关爱下一代")

14．诉诸权威（ Appeal to Authority )：滥用权威背书（如"某明星推荐保健品，故其有效")

15．诉诸传统（ Appeal to Tradition )：因历史悠久即认定合理（如"中医存在千年，所以无需现代验证")

16．诉诸新潮（ Appeal to Novelty )：认为新技术必然优越（如"区块链万能论")

17．情感替代（ Affective Heuristic )：因喜好影响风险评估（如"喜欢某品牌就认定其产品安全")

18．光环效应（ Halo Effect )：因某一优点推定整体优秀（如"名校毕业生必然能力强")

四、语言与框架陷阱

19．语义模糊（ Equivocation )：利用多义词混淆概念（如"人权包含生存权，故杀人犯也有人权应免死")

20．稻草人谬误（ Straw Man )：曲解对方论点再加以反驳（如将"减少碳排放"歪曲为"禁止工业发展")

21．滑坡谬误（ Slippery Slope )：无合理因果链的极端推断（如"允许同性婚姻将导致人兽婚姻合法化")

22．框架效应（ Framing Effect )：同一事实因表述方式改变认知（如"手术成功率 90%" vS “死亡率 10%”)

23．误用类比（ False Analogy ):忽略关键差异的类比推理（如"国家如家庭，必须由家长独裁")

24．语义诱导（ Loaded Language )：用情感词汇操控判断（如"野蛮拆迁" vs “城市更新”)

五、社会认知偏差

25．从众偏误（ Bandwagon Fallacy )：因多数人认同即认定正确（如"全球 60％人信教，故神存在")

26．群体极化＊( Group Polarization )：群体讨论强化极端立场（如网络暴力升级）

27．逆火效应＊( Backfire Effect )：反面证据反而加强原有错误信念

28．达克效应（ Dunning - Kruger Effect )：低能力者高估自身认知水平

29．基本归因错误（ Fundamental Attribution

Error )：高估个人特质影响，低估情境因素

（如"穷人因懒惰致贫")

30．公正世界谬误（ Just - World Fallacy )：认为受害必有过错（如"被性侵者因穿着暴露")

六、概率与统计盲区

31．赌徒谬误（ Gambler ’ s Fallacy )：误认独立事件的关联性（如"连开 5 次大，下次必开小")

32．热手谬误（ Hot Hand Fallacy )：高估连胜事件的持续性（如"球员连续得分被认为手感火

热")

33．忽略样本量（ Law of Small Numbers )：用小样本得出普遍结论（如"新药 3 人试用有效即推广")

34．辛普森悖论（ Simpson ’ s Paradox )：分组数据趋势与整体相反（如某药在各亚组有效，但整体无效）

35．均值回归（ Regression to the Mean )：将自然波动误认为干预效果（如严厉惩罚后学生成绩"提升")

七、决策与行为漏洞

36．沉没成本谬误（ Sunk Cost Fallacy )：因已投入资源继续错误决策（如"亏损股票不肯抛售")

37．锚定效应（ Anchoring Effect )：初始信息过度影响后续判断（如先看高价后觉低价划算）

38．现状偏好（ Status Quo Bias )：非理性维持当前状态（如默认选项设置对器官捐献率的影响）

39．损失厌恶（ Loss Aversion )：对损失的恐惧压倒收益可能（如宁可不赚 100 元，也不愿亏 50

元）

40．可得性启发（ Availability Heuristic )：用易回忆事件评估概率（如高估空难风险）

八、复杂系统误判

41．线性外推谬误（ Linear Extrapolation )：忽视复杂系统的非线性变化（如"人口按当前增速百年后爆炸")

42．局部优化陷阱（ Suboptimization )：追求子系统最优损害整体（如 KPI 驱动下的部门对立）

43．忽略反馈延迟（ Delay Ignorance )：未考虑行动与结果的时滞（如环保政策短期未见效即放

弃）

44．系统归因简化（ Reductionism )：用单一因素解释复杂现象（如"经济危机源于贪婪")

45．指标扭曲（ Goodhart ’ s Law )：过度优化测量指标导致目标偏离（如学校为升学率压制素质教育）

九、元认知缺陷

46．认知闭合需求（ Need for Closure )：为求确定性接受低质量答案

47，过度自信效应（ Overconfidence Effect ):

高估自身判断准确性（如 90％司机认为技术高于平均水平）

48，知识诅咒（ Curse of Knowledge )：专家无法理解新手认知盲区（如教授用术语向公众科普）

---

via:

• 概率的谬误，概率的概率，概率的哲学
  https://mp.weixin.qq.com/s/D_G5nhctcTHtwszhID1FBQ
• 揭秘基础率谬误：为何我们总是被细节迷惑，忽略了真实概率？
  https://mp.weixin.qq.com/s/b3y7sS0BmIOHDzHB7rn4HA
• 7 个基本逻辑概率谬误
  https://mp.weixin.qq.com/s/YtQ2nWQU1zwlp5h0ZU6Wbg
• 许兴华——揭秘常见的概率谬误：让我们避免陷入数学陷阱
  https://mp.weixin.qq.com/s/8k9DMkLXcBtr3WyR9qT_9g
• 朴素逻辑的 48 种典型认知漏洞
  https://mp.weixin.qq.com/s/aqgB8M4zO-PZLlm45e-CcQ