向量 | 内积 / 外积 / 点积 / 叉积 | 几何意义 / 应用

注：本文为 “向量内积与外积” 相关合辑。
略排未全校去重。
如有内容异常，请看原文。

---

向量点乘（即内积）和叉乘（即外积、向量积）区别与意义分析

Lu_gl 于 2022-01-05 20:20:54 发布

向量之间的叉乘和点乘，概念易混淆，现对其进行详细分析介绍。

首先，向量（Vector） 是几乎所有几何问题中的一个基本点。向量的定义包含方向和一个数（长度）。

在二维空间中，一个向量可用一对 $x$ 和 $y$ 来表示。向量：既有方向又有大小的量。 通常情况下会将向量放到坐标系中，常用的是笛卡尔坐标系，向量起始点通常放到原点（注：没有固定的起点，只要方向相同，大小相等，就认为两向量是相同的，但为了用数值坐标来表示向量，将起始点放到原点）。

一、点乘 （Dot Product）

向量的点乘，也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。点乘，也叫数量积。结果是一个向量在另一个向量方向上投影的长度，是一个标量。

假设向量 $\mathbf{a}$ 和向量 $\mathbf{b}$：

$$\begin{array}{rl}& a=\left[a_1,a_2,\dots a_n\right]\\ & b=\left[b_1,b_2,\dots b_n\right]\end{array}$$

$\mathbf{a}$ 和 $\mathbf{b}$ 的点积公式（要求一维向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 的行列数相同）为：

$$\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2+a_3{b}_3$$

对应点乘的几何意义为

点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在 $\mathbf{b}$ 向量在 $\mathbf{a}$ 向量方向上的投影，有公式：

$$\mathbf{a}\cdot \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos (\theta )$$

$\theta$ 是向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 之间的夹角。这里 $\Vert \mathbf{a}\Vert$ 我们称为向量 $\mathbf{a}$ 的模（norm），也就是 $\mathbf{a}$ 的长度，在二维空间中就是 $\Vert \mathbf{a}\Vert =\sqrt{x^2+y^2}$。这样就可以很容易计算两条线的夹角：

$$\cos (\theta )=\frac{\mathbf{a}\cdot \mathbf{b}}{\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert }$$

向量差的模长与向量夹角推导

对于推导过程可以稍微利用余弦定理如下：

首先看一下向量组成：

设向量关系为 $\mathbf{c}=\mathbf{a}-\mathbf{b}$（$\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$ 均为向量），$\theta$ 为 $\mathbf{a}$ 与 $\mathbf{b}$ 的夹角（取值范围 $[0,\pi ]$），$\Vert \mathbf{a}\Vert$、$\Vert \mathbf{b}\Vert$、$\Vert \mathbf{c}\Vert$ 分别表示三个向量的模长（非负实数）。

1. 由三角形余弦定理建立关系
   当 $\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$ 构成三角形（或共线）时，根据三角形余弦定理，$\mathbf{c}$ 的模长平方满足：
   $$\Vert \mathbf{c}{\Vert }^2=\Vert \mathbf{a}{\Vert }^2+\Vert \mathbf{b}{\Vert }^2-2\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos \theta$$

2. 用向量点积展开 $\Vert \mathbf{c}{\Vert }^2$
   由 $\mathbf{c}=\mathbf{a}-\mathbf{b}$，结合“向量模长的平方等于向量自身的点积”（即 $\Vert \vec{x}{\Vert }^2=\vec{x}\cdot \vec{x}$），得：
   $$\Vert \mathbf{c}{\Vert }^2=(\mathbf{a}-\mathbf{b})\cdot (\mathbf{a}-\mathbf{b})$$

   按点积分配律、交换律展开，并利用 $\mathbf{a}\cdot \mathbf{a}=\Vert \mathbf{a}{\Vert }^2$、$\mathbf{b}\cdot \mathbf{b}=\Vert \mathbf{b}{\Vert }^2$ 化简：
   $$(\mathbf{a}-\mathbf{b})\cdot (\mathbf{a}-\mathbf{b})=\mathbf{a}\cdot \mathbf{a}-2\mathbf{a}\cdot \mathbf{b}+\mathbf{b}\cdot \mathbf{b}=\Vert \mathbf{a}{\Vert }^2+\Vert \mathbf{b}{\Vert }^2-2\mathbf{a}\cdot \mathbf{b}$$

3. 求解向量夹角 $\theta$
   联立步骤1与步骤2的结果，消去 $\Vert \mathbf{c}{\Vert }^2$ 并约去同类项，结合点积的几何定义 $\mathbf{a}\cdot \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos \theta$，整理得夹角余弦值：
   $$\cos \theta =\frac{\mathbf{a}\cdot \mathbf{b}}{\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert }$$

   若需明确夹角 $\theta$，可通过反余弦函数求解：
   $$\theta =\arccos \left(\frac{\mathbf{a}\cdot \mathbf{b}}{\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert }\right)$$

根据这个公式就可以计算向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 之间的夹角。 从而就可以进一步判断这两个向量是否是同一方向，是否正交（也就是垂直）等方向关系，具体对应关系为：

$$\begin{array}{ccl}\mathbf{a}\cdot \mathbf{b}& >0& \text{方向基本相同，夹角在 }{0}^{\circ }\text{ 到 }90^{\circ }\text{ 之间}\\ \mathbf{a}\cdot \mathbf{b}& =0& \text{正交，相互垂直}\\ \mathbf{a}\cdot \mathbf{b}& <0& \text{方向基本相反，夹角在 }90^{\circ }\text{ 到 }180^{\circ }\text{ 之间}\end{array}$$

总结就是：

假如向量 $\mathbf{a}$ 为 $(x_1,y_1)$，向量 $\mathbf{b}$ 为 $(x_2,y_2)$，

点积（也叫内积）结果为 $\mathbf{a}\cdot \mathbf{b}=x_1{x}_2+y_1{y}_2=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos (\theta )$，可以理解为向量 $\mathbf{a}$ 在向量 $\mathbf{b}$ 上投影的长度乘以向量 $\mathbf{b}$ 的长度。

应用：

二、叉乘（cross product）

两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量，并且两个向量的叉积与这两个向量组成的坐标平面垂直。

对于向量 $\mathbf{a}$ 和向量 $\mathbf{b}$：

$$\begin{array}{rl}& a=\left(x_1,y_1,z_1\right)\\ & b=\left(x_2,y_2,z_2\right)\end{array}$$

$\mathbf{a}$ 和 $\mathbf{b}$ 的叉乘公式为，其中 $\mathbf{i}=(1,0,0)$、$\mathbf{j}=(0,1,0)$、$\mathbf{k}=(0,0,1)$：

$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$$

根据 $\mathbf{i}$、$\mathbf{j}$、$\mathbf{k}$ 间关系，有：

$$\mathbf{a}\times \mathbf{b}=(a_2{b}_3-a_3{b}_2)\mathbf{i}-(a_1{b}_3-a_3{b}_1)\mathbf{j}+(a_1{b}_2-a_2{b}_1)\mathbf{k}$$

对应叉乘的几何意义为

在三维几何中，向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 向量构成的平面。 叉乘的结果是个向量，方向在 $z$ 轴上，在二维空间里，让我们暂时忽略它的方向，将结果看成一个向量，那么这个结果类似于上述的点积，有公式：

$$\mathbf{a}\times \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \sin (\theta )$$

然而角度 $\theta$ 和上面点乘的角度有一点点不同，它是有正负的，是指从 $\mathbf{a}$ 到 $\mathbf{b}$ 的角度。因此，向量的外积不遵守乘法交换率，因为 $\mathbf{a}\times \mathbf{b}=-\mathbf{b}\times \mathbf{a}$。在物理学中，已知力与力臂求外积，就是向量的外积，即叉乘。

在 3D 图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于 $\mathbf{a}$、$\mathbf{b}$ 的法向量，从而构建 $X$、$Y$、$Z$ 坐标系。 如下图所示：

在二维空间中，叉乘还有另外一个几何意义就是：$\mathbf{a}\times \mathbf{b}$ 等于由向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 构成的平行四边形的面积。

叉积的绝对值就是 $\mathbf{A}$ 和 $\mathbf{B}$ 为两边说形成的平行四边形的面积。也就是 $\mathbf{AB}$ 所包围三角形面积的两倍。在计算面积时，我们要经常用到叉积。

方向判定：

向量 $\mathbf{c}$ 的方向与 $\mathbf{a}$、$\mathbf{b}$ 所在的平面垂直，且方向要用“右手法则”判断。判断方法如下：

1. 右手掌张开，四指并拢，大拇指垂直于四指指向的方向。
2. 伸出右手，四指弯曲，四指与 $\mathbf{A}$ 旋转到 $\mathbf{B}$ 方向一致，那么大拇指指向为 $\mathbf{C}$ 向量的方向。

总结就是：

假如向量 $\mathbf{a}$ 为 $(x_1,y_1)$，向量 $\mathbf{b}$ 为 $(x_2,y_2)$，

叉积（也叫外积）的模为 $\mathbf{a}\times \mathbf{b}=x_1{y}_2-x_2{y}_1=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \sin (\theta )$，可以理解为平行四边形的有向面积（三维以上为体积）。外积的方向垂直于这两个方向。

应用：

---

带你一次搞懂点积（内积）、叉积（外积）

隐私无忧 已于 2022-10-09 20:47:37 修改

1. 向量的点积与叉积

1.1 向量的点积

数量积又称标量积（Scalar product）、点积（Dot product），在欧几里得空间（Euclidean space）中称为内积（Inner product），对应元素相乘相加，结果是一个标量（即一个数）。

对于向量 $\mathbf{a}=(a_1,a_2)$，$\mathbf{b}=(b_1,b_2)$，两者的数量积为：

$$\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2$$

$\mathbf{a}\cdot \mathbf{b}$ 的几何意义是 $\mathbf{a}$ 在 $\mathbf{b}$ 方向上的投影（仅在二维、三维空间向量有意义）：

$$\mathbf{a}\cdot \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos (\theta )$$

其中，$\Vert \mathbf{a}\Vert$、$\Vert \mathbf{b}\Vert$ 分别为向量 $\mathbf{a}$、$\mathbf{b}$ 的模，$\theta$ 为向量 $\mathbf{a}$、$\mathbf{b}$ 的夹角。

对于 $n$ 维向量 $\mathbf{a}=(a_1,a_2,\dots ,a_n)$，$\mathbf{b}=(b_1,b_2,\dots ,b_n)$，两者的数量积为：

$$\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n$$

numpy 中使用 np.dot 或 numpy.inner() 实现向量的点积

举例

$$\mathbf{a}=(1,2,3),\mathbf{b}=(4,5,6)$$

$$\mathbf{a}\cdot \mathbf{b}=1\times 4+2\times 5+3\times 6=32$$

import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
## 数量积  使用 np.dot 或 np.inner
print(np.dot(a, b))

1.2 向量的叉积

向量积又称矢量积（Vector product）、叉积（Cross product）、外积（Outer product），结果是一个向量。

对于向量 $\mathbf{a}=(a_1,a_2,a_3)$，$\mathbf{b}=(b_1,b_2,b_3)$，两者的叉积为 $\mathbf{a}$ 和 $\mathbf{b}$ 的法向量，该向量垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 构成的平面：

$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$$

$$=(a_2{b}_3-b_2{a}_3)\mathbf{i}-(a_1{b}_3-b_1{a}_3)\mathbf{j}+(a_1{b}_2-b_1{a}_2)\mathbf{k}$$

其中，$\mathbf{i}$、$\mathbf{j}$、$\mathbf{k}$ 分别是 $X$、$Y$、$Z$ 轴方向的单位向量。

该向量的模：

$$\Vert \mathbf{a}\times \mathbf{b}\Vert =\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \sin (\theta )$$

其中，$\Vert \mathbf{a}\Vert$、$\Vert \mathbf{b}\Vert$ 分别为向量 $\mathbf{a}$、$\mathbf{b}$ 的模，$\theta$ 为向量 $\mathbf{a}$、$\mathbf{b}$ 的夹角。

即，叉积的长度 $\Vert \mathbf{a}\times \mathbf{b}\Vert$ 为向量 $\mathbf{a}$、$\mathbf{b}$ 共起点时，构成平行四边形的面积。

numpy 中使用 np.cross 实现向量的叉积

举例

$$\mathbf{a}=(1,2,3),\mathbf{b}=(4,5,6)$$

$$\mathbf{a}\times \mathbf{b}=(2\times 6-3\times 5,4\times 3-1\times 6,1\times 5-2\times 4)=(-3,6,-3)$$

import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
## 叉积  使用 np.cross
print(np.cross(a, b))

点积与叉积小结：

名称	点积 / 数量积 / 标量积 / 内积 /	叉积 / 向量积 / 矢量积 / 外积 /
输入（以 $R^3$ 为例）	$\mathbf{a}=(a_1,a_2,a_3)$，$\mathbf{b}=(b_1,b_2,b_3)$	$\mathbf{a}=(a_1,a_2,a_3)$，$\mathbf{b}=(b_1,b_2,b_3)$
运算	$\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2+a_3{b}_3$	$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$
输出	数值（标量）：$|\mathbf{a}||\mathbf{b}|\cos (\theta )$	向量（矢量）：$|\mathbf{a}||\mathbf{b}|\sin (\theta )$

注：数量、向量常用于数学；而标量、矢量常用于物理

2 矩阵的点积与叉积

2.1 矩阵的点积

对于 $A$ 矩阵（$m\times s$ 阶），$B$ 矩阵（$s\times n$ 阶）（$A$ 的列数与 $B$ 的行数相等），

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1s}\\ a_{21}& a_{22}& \cdots & a_{2s}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{ms}\end{array}\right],B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ b_{s1}& b_{s2}& \cdots & b_{sn}\end{array}\right]$$

两者的点积，即矩阵相乘的结果 $C=AB$ 是 $m\times n$ 阶矩阵，

$$C=AB=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1n}\\ c_{21}& c_{22}& \cdots & c_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ c_{m1}& c_{m2}& \cdots & c_{mn}\end{array}\right]$$

其中，矩阵 $C$ 中的元素满足

$$c_{ij}=\sum _{k=1}^s{a}_{ik}{b}_{kj}$$

举例

$$A_1=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B_1=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]$$

$$A_2=\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right],B_2=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

$$A_1{B}_1=\left[\begin{array}{cc}19& 22\\ 43& 50\end{array}\right],A_2{B}_2=\left[\begin{array}{c}14\\ 14\end{array}\right]$$

numpy 实现

import numpy as np
A1 = np.array([[1, 2], [3, 4]])
B1 = np.array([[5, 6], [7, 8]])
A2 = np.array([[1, 2, 3], [1, 2, 3]])
B2 = np.array([1, 2, 3])
## 数量积  使用 np.dot
print(np.dot(A1, B1))
print(np.dot(A2, B2))

此外，numpy 提供了 numpy.inner() 函数，从字面意思理解是内积，其针对向量 numpy.inner() 与 numpy.dot() 输出一致，但针对矩阵有所不同。

print(np.inner(A1, B1))

输出为

$$\left[\begin{array}{cc}17& 23\\ 39& 53\end{array}\right]$$

其中，

$$17=1\times 5+2\times 6,23=1\times 7+2\times 8$$

$$39=3\times 5+4\times 6,53=3\times 7+4\times 8$$

print(np.inner(A2, B2))

输出为

$$\left[\begin{array}{c}14\\ 14\end{array}\right]$$

2.2 矩阵的叉积

针对矩阵并不存在叉积的概念，numpy 中针对矩阵的叉积运算是按照向量的叉积进行运算。

举例

$$A_1=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B_1=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]$$

$$A_2=\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right],B_2=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

$$A_1\times B_1=\left[\begin{array}{c}-4\\ -4\end{array}\right],A_2\times B_2=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

numpy 实现

import numpy as np
A1 = np.array([[1, 2], [3, 4]])
B1 = np.array([[5, 6], [7, 8]])
A2 = np.array([[1, 2, 3], [1, 2, 3]])
B2 = np.array([1, 2, 3])
## 叉积  使用 np.cross
print(np.cross(A1, B1))
print(np.cross(A2, B2))

3. 元素积

元素积（element-wise product, point-wise product） 又称 哈达玛积（Hadamard product）、舒尔积、逐项积，对应元素相乘，结果还是向量/矩阵。

对于 $n$ 维向量 $\mathbf{a}=(a_1,a_2,\dots ,a_n)$，$\mathbf{b}=(b_1,b_2,\dots ,b_n)$，两者的元素积为：

$$\mathbf{a}\ast \mathbf{b}=(a_1{b}_1,a_2{b}_2,\dots ,a_n{b}_n)$$

对于同阶矩阵 $A$（$m\times n$ 阶），$B$（$m\times n$ 阶），两者的哈达玛积为：

$$A\circ B=\left[\begin{array}{cccc}{a}_{11}{b}_{11}& a_{12}{b}_{12}& \cdots & a_{1n}{b}_{1n}\\ a_{21}{b}_{21}& a_{22}{b}_{22}& \cdots & a_{2n}{b}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}{b}_{m1}& a_{m2}{b}_{m2}& \cdots & a_{mn}{b}_{mn}\end{array}\right]$$

numpy 中使用 np.multiply 或 * 实现元素积

举例

向量：

$$\mathbf{a}=(1,2,3),\mathbf{b}=(4,5,6)$$

$$\mathbf{a}\circ \mathbf{b}=(4,10,18)$$

矩阵：

$$A_1=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B_1=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]$$

$$A_2=\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right],B_2=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

$$A_1\circ B_1=\left[\begin{array}{cc}5& 12\\ 21& 32\end{array}\right],A_2\circ B_2=\left[\begin{array}{ccc}1& 4& 9\\ 1& 4& 9\end{array}\right]$$

numpy 实现

import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
A1 = np.array([[1, 2], [3, 4]])
B1 = np.array([[5, 6], [7, 8]])
A2 = np.array([[1, 2, 3], [1, 2, 3]])
B2 = np.array([1, 2, 3])
## 元素积  使用 np.multiply 或 *
print(np.multiply(a, b))
print(np.multiply(A1, B1))
print(np.multiply(A2, B2))  # 阶数不一致的，numpy 将进行广播确保一致

4. 克罗内克积

克罗内克积（Kronecker product）是 两个任意大小的矩阵间的运算。

对于 $A$ 矩阵（$m\times n$ 阶），$B$ 矩阵（$p\times q$ 阶）：

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right],B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1q}\\ b_{21}& b_{22}& \cdots & b_{2q}\\ ⋮& ⋮& \ddots & ⋮\\ b_{p1}& b_{p2}& \cdots & b_{pq}\end{array}\right]$$

两者的克罗内克积 $C=A\otimes B$ 是 $mp\times nq$ 阶的分块矩阵：

$$C=A\otimes B=\left[\begin{array}{cccc}{a}_{11}B& a_{12}B& \cdots & a_{1n}B\\ a_{21}B& a_{22}B& \cdots & a_{2n}B\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}B& a_{m2}B& \cdots & a_{mn}B\end{array}\right]$$

更具体而言：

$$C=\left[\begin{array}{cccccccccc}{a}_{11}{b}_{11}& a_{11}{b}_{12}& \cdots & a_{11}{b}_{1q}& \cdots & \cdots & a_{1n}{b}_{11}& a_{1n}{b}_{12}& \cdots & a_{1n}{b}_{1q}\\ a_{11}{b}_{21}& a_{11}{b}_{22}& \cdots & a_{11}{b}_{2q}& \cdots & \cdots & a_{1n}{b}_{21}& a_{1n}{b}_{22}& \cdots & a_{1n}{b}_{2q}\\ ⋮& ⋮& \ddots & ⋮& & & ⋮& ⋮& \ddots & ⋮\\ a_{11}{b}_{p1}& a_{11}{b}_{p2}& \cdots & a_{11}{b}_{pq}& \cdots & \cdots & a_{1n}{b}_{p1}& a_{1n}{b}_{p2}& \cdots & a_{1n}{b}_{pq}\\ ⋮& ⋮& & ⋮& \ddots & & ⋮& ⋮& & ⋮\\ ⋮& ⋮& & ⋮& & \ddots & ⋮& ⋮& & ⋮\\ a_{m1}{b}_{11}& a_{m1}{b}_{12}& \cdots & a_{m1}{b}_{1q}& \cdots & \cdots & a_{mn}{b}_{11}& a_{mn}{b}_{12}& \cdots & a_{mn}{b}_{1q}\\ a_{m1}{b}_{21}& a_{m1}{b}_{22}& \cdots & a_{m1}{b}_{2q}& \cdots & \cdots & a_{mn}{b}_{21}& a_{mn}{b}_{22}& \cdots & a_{mn}{b}_{2q}\\ ⋮& ⋮& \ddots & ⋮& & & ⋮& ⋮& \ddots & ⋮\\ a_{m1}{b}_{p1}& a_{m1}{b}_{p2}& \cdots & a_{m1}{b}_{pq}& \cdots & \cdots & a_{mn}{b}_{p1}& a_{mn}{b}_{p2}& \cdots & a_{mn}{b}_{pq}\end{array}\right]$$

numpy 中使用 np.kron 实现

举例

$$A_1=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right],B_1=\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right]$$

$$A_2=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B_2=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]$$

$$A_3=\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right],B_3=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

$$A_1\otimes B_1=\left[\begin{array}{ccc}4& 5& 6\\ 8& 10& 12\\ 12& 15& 18\end{array}\right]$$

$$A_2\otimes B_2=\left[\begin{array}{cccc}5& 6& 10& 12\\ 7& 8& 14& 16\\ 15& 18& 20& 24\\ 21& 24& 28& 32\end{array}\right]$$

$$A_3\otimes B_3=\left[\begin{array}{ccccccccc}1& 2& 3& 2& 4& 6& 3& 6& 9\\ 1& 2& 3& 2& 4& 6& 3& 6& 9\end{array}\right]$$

numpy 实现

import numpy as np
A1 = np.array([1, 2, 3])
B1 = np.array([4, 5, 6])
A2 = np.array([[1, 2], [3, 4]])
B2 = np.array([[5, 6], [7, 8]])
A3 = np.array([[1, 2, 3], [1, 2, 3]])
B3 = np.array([1, 2, 3])
## 克罗内克积  使用 np.kron
print(np.kron(A1, B1))
print(np.kron(A2, B2))
print(np.kron(A3, B3))

---

点积、叉积、内积、外积【汇总对比】

Dust_Evc 于
2022-10-24 21:39:26 发布

点积（Dot Product）

又称标量积、数量积（Scalar Product）。它是两个数字序列对应条目乘积的和。在欧几里得几何里，两个向量笛卡尔坐标的点积应用广泛。它常被称作欧几里得空间的内积（或极少被称为投影积），是内积的一种特殊情形，不过并非是能在欧几里得空间上定义的唯一内积。

从代数角度看，点积是两个数字序列对应条目乘积的和；从几何角度看，它是两个向量的欧几里得模长与它们夹角余弦的乘积。当使用笛卡尔坐标时，这两种定义是等价的。在现代几何中，欧几里得空间通常借助向量空间来定义。此时，点积被用于定义长度（向量的长度是该向量自身点积的平方根）和角度（两个向量夹角的余弦等于它们的点积与它们模长乘积的商）。

代数定义

几何定义

与内积的关系

叉积（Cross Product）

或向量积（Vector Product）（有时也称为有向面积积，以突出其几何意义），是在三维有向欧几里得向量空间中定义的运算，用符号

$\times$ 表示。给定两个线性无关的向量 $\mathbf{a}$ 和 $\mathbf{b}$ ，叉积 $\mathbf{a}\times \mathbf{b}$ （读作“$a$ cross $b$ ”）是一个垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 的向量，因而也垂直于包含它们的平面。

定义

下图为使用 Sarrus 规则得到

$\mathbf{a}$ 和
$\mathbf{b}$ 的叉积：

叉积也可表示为形式行列式：

$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$$

该行列式可通过 Sarrus 规则或余子式展开来计算。利用 Sarrus 规则，其展开式为：

$$\begin{array}{rl}\mathbf{a}\times \mathbf{b}& =(a_2{b}_3\mathbf{i}+a_3{b}_1\mathbf{j}+a_1{b}_2\mathbf{k})-(a_3{b}_2\mathbf{i}+a_1{b}_3\mathbf{j}+a_2{b}_1\mathbf{k})\\ & =(a_2{b}_3-a_3{b}_2)\mathbf{i}+(a_3{b}_1-a_1{b}_3)\mathbf{j}+(a_1{b}_2-a_2{b}_1)\mathbf{k}\end{array}$$

沿第一行用余子式展开，展开式为：

$$\begin{array}{rl}\mathbf{a}\times \mathbf{b}& =\left|\begin{array}{cc}{a}_2& a_3\\ b_2& b_3\end{array}\right|\mathbf{i}-\left|\begin{array}{cc}{a}_1& a_3\\ b_1& b_3\end{array}\right|\mathbf{j}+\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|\mathbf{k}\\ & =(a_2{b}_3-a_3{b}_2)\mathbf{i}-(a_1{b}_3-a_3{b}_1)\mathbf{j}+(a_1{b}_2-a_2{b}_1)\mathbf{k}\end{array}$$

这直接给出了结果的分量。

几何意义

内积（Inner Product）

空间中两个向量的内积是一个标量，通常用尖括号（如 $\langle \cdot,

\cdot \rangle$ ）表示。内积空间是欧几里得向量空间的推广，在欧几里得向量空间中，内积就是笛卡尔坐标的点积或标量积。

无穷维内积空间在泛函分析中应用广泛。复数域上的内积空间有时被称为酉空间。向量空间中内积概念的首次使用归功于朱塞佩·皮亚诺（Giuseppe Peano），于1898年提出。

使用内积定义的两个向量之间角度的几何解释（ $\vert \mathbf{x}

\vert$ 与 $|\mathbf{y}|$ 为范数在二维、三维空间的表现）。

定义

例子

外积（Outer Product）

在线性代数里，两个坐标向量的外积是一个矩阵。若这两个向量的维度分别为 $n$ 和 $m$ ，那么它们的外积是一个 $n\times m$ 的矩阵。更一般地，给定两个张量（多维数字数组），它们的外积是张量。张量的外积也被称为张量积，可用于定义张量代数。

定义

与欧几里得内积对比

张量的外积

---

向量的内积与外积

木木 发布于 2019-11-11 23:18

一、向量的内积和几何意义（点乘）

对于向量 $\mathbf{a}$ 和向量 $\mathbf{b}$：

$$\begin{array}{rl}& a=\left[a_1,a_2,\dots a_n\right]\\ & b=\left[b_1,b_2,\dots b_n\right]\end{array}$$

1. $\mathbf{a}$ 和 $\mathbf{b}$ 的内积公式为：

   $$\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2+a_3{b}_3$$

   要求一维向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 的行列数相同。

2. 内积的几何意义

   点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在 $\mathbf{b}$ 向量在 $\mathbf{a}$ 向量方向上的投影。

二、向量的外积和几何意义（叉乘）

两个向量的外积，又叫向量积、叉乘等。外积的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。

对于向量 $\mathbf{a}$ 和向量 $\mathbf{b}$：

$$\begin{array}{rl}& a=\left(x_1,y_1,z_1\right)\\ & b=\left(x_2,y_2,z_2\right)\end{array}$$

1. $\mathbf{a}$ 和 $\mathbf{b}$ 的外积公式为：

   $$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$$

   其中：

   $$\mathbf{i}=(1,0,0),\mathbf{j}=(0,1,0),\mathbf{k}=(0,0,1)$$

   根据 $\mathbf{i}$、$\mathbf{j}$、$\mathbf{k}$ 间关系，有：

   $$\mathbf{a}\times \mathbf{b}=(a_2{b}_3-a_3{b}_2)\mathbf{i}-(a_1{b}_3-a_3{b}_1)\mathbf{j}+(a_1{b}_2-a_2{b}_1)\mathbf{k}$$

2. 叉乘几何意义

   在三维几何中，向量 $\mathbf{a}$ 和向量 $\mathbf{b}$ 的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 向量构成的平面。

---

真一文搞懂：内积、外积及其衍生（内积：点积、数量积、标量积；外积：叉积、叉乘、向量积、张量积）

我头上有犄角 编辑于 2024-03-08 09:44・广东

首先说明一下，内积 和 外积 都是一种 广义的称呼，我们 最常见的内积是点积（数量积、标量积和点积定义相同），即对应元素乘然后累加；而我们最容易弄错外积的定义，我们理解的两个向量运算得到第三个向量，且其方向垂直于另外两个向量的运算严格上叫叉积、叉乘、向量积。

而非外积，外积有其单独定义，其对向量运算的结果为矩阵。

首先假设有以下两个向量：

$$\mathbf{a}=\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right],\mathbf{b}=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]$$

一、内积（点积、数量积、标量积）

欧氏空间中 内积 的定义一般没有什么歧义，比较相似的 内乘 一词定义为向量空间和外代数中，和流型相关。而点积和内积的具体关系如下：

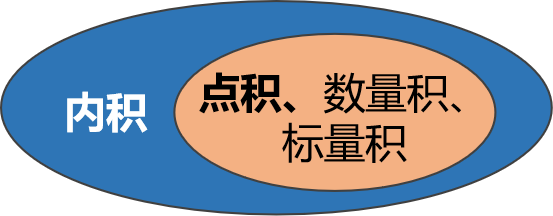
内积定义比点积宽泛，内积在欧氏空间中则被称为点积。

在线性代数中，内积是定义在向量空间上的一种运算，它通常满足对称性、线性性和正定性。内积 最常见的形式是 欧氏空间 中的内积，也就是常说的 点积（dot product），点积也被称为 数量积、标量积。

注：以下我们所提到的内积均指的是欧氏空间中的内积，即点积。

1. 内积的表示

$$\text{dot}(\mathbf{a},\mathbf{b})=a_1{b}_1+a_2{b}_2+a_3{b}_3$$

还有一种表示形式为

$$\text{dot}(\mathbf{a},\mathbf{b})=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos (\theta )$$

2. 内积的意义

投影和分解：点积可以用来描述一个向量在另一个向量方向上的投影。给定两个向量 $\mathbf{a}$ 和 $\mathbf{b}$，它们的点积 $\mathbf{a}\cdot \mathbf{b}$ 表示 $\mathbf{a}$ 在 $\mathbf{b}$ 方向上的投影的长度，或者 $\mathbf{b}$ 在 $\mathbf{a}$ 方向上的投影的长度。这在物理学和工程学中经常用于分解力、速度、加速度等向量。

几何关系：点积可以用来计算向量之间的夹角，$\mathbf{a}\cdot \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos (\theta )$，其中 $\cos (\theta )$ 是 $\mathbf{a}$ 和 $\mathbf{b}$ 之间的夹角。通过这个公式可以比较容易地计算出两个向量之间的角度。

相关性：内积可以理解为表示了两个向量之间的相干性，若两个向量正交（无相干性），则点积为 0；而点积越大表示两个向量的相干性越强（但局限性是这点相干性只和角度有关，和 $\mathbf{a}$ 和 $\mathbf{b}$ 的长度值无关）。在信号处理和模式识别以及深度学习方法中常用到这种方式来计算信号之间的相似度或相关性。

基向量：通过投影这种方式我们可以将一个向量从一个基投影到另一个基，假如一个向量本身在三维空间（三个基），它原本的基为

二、外积（叉积、叉乘、向量积）

外积是更广义的说法，宽松的说，它在一定的语境中和叉积、叉乘、向量积都表示求垂直于两个向量的新向量，但是在更严格的语境中

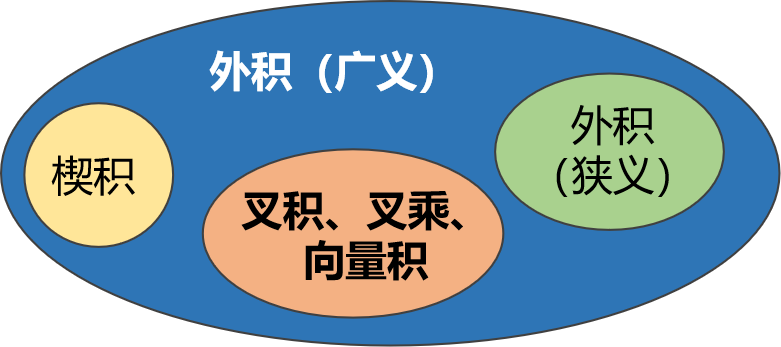
广义上外积的分类

外积可以分为以下几种含义，维基百科中注明了这几个的差别：

• External product，又名 叉积（英语：cross product）和 向量积（英语：vector product），常写为 $\mathbf{a}\times \mathbf{b}$
• Exterior product，又名 楔积（英语：wedge product），常写为 $\mathbf{a}\wedge \mathbf{b}$
• Outer product，见 外积 (张量积)，常写为 $\mathbf{a}\otimes \mathbf{b}$

接下来我们一个一个区分它们

1. 叉积、叉乘、向量积

在 数学 和 向量代数 领域，外积（external product）又称 叉积、叉乘、向量积，是对 三维空间 中的两个向量的二元运算，英文中的 (external, cross, vector) product 均为此定义，同时也是最广为人知的一个外积的定义，此外积仅在三维空间中定义。

外积 $\mathbf{a}\times \mathbf{b}$ 是与 $\mathbf{a}$ 和 $\mathbf{b}$ 都垂直的向量。其方向由右手定则决定，模长等于以两个向量为边的平行四边形的面积。公式定义为：

$$\mathbf{a}\times \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \sin (\theta )\mathbf{n}$$

其中 $\mathbf{n}$ 表示垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 的单位向量 ($\mathbf{i}$, $\mathbf{j}$, $\mathbf{k}$)，具体来说，其结果为以下行列式：

$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$$

结果为：

$$\mathbf{a}\times \mathbf{b}=(a_2{b}_3-a_3{b}_2)\mathbf{i}-(a_1{b}_3-a_3{b}_1)\mathbf{j}+(a_1{b}_2-a_2{b}_1)\mathbf{k}$$

2. 楔积

此定义为外代数中的内容，一种将两个向量（或更高阶的对象）结合成一个新的几何对象的运算。楔积的结果可以表示 面积、体积 或 更高维形式 的概念，在 几何、物理学 和 微分几何 中有广泛的应用。

对于两个向量 $\mathbf{a}$ 和 $\mathbf{b}$，它们的楔积 $\mathbf{a}\wedge \mathbf{b}$ 可以表示为一个二阶外积（2-形式），它携带了这两个向量所张成的平行四边形的面积和方向信息。在三维空间中，楔积的结果可以通过如下矩阵的行列式来计算：

$$\mathbf{a}\wedge \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|$$

其中 $\mathbf{i}$，$\mathbf{j}$，$\mathbf{k}$ 是单位向量，$a_x$, $a_y$, $a_z$ 和 $b_x$, $b_y$, $b_z$ 分别是向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的分量。

楔积（外积）和 叉积 虽然在三维空间中可以给出相似的几何信息，但它们在本质上是不同的数学对象，具有不同的属性和应用范围。这里是它们之间的一些 主要区别：

1. 数学性质：

• 楔积：楔积是一种在外代数中定义的运算，它可以应用于任意维度的空间，并且可以用来定义高阶的几何对象。楔积的结果是一个外积或外形式，不局限于向量，且在维度大于 3 时依然有效。楔积具有反对称性，即 $\mathbf{a}\wedge \mathbf{b}=-\mathbf{b}\wedge \mathbf{a}$。
• 叉积：叉积是一种特定于三维空间的运算，结果是一个新的向量，该向量垂直于原始两个向量所在的平面。叉积遵循右手定则，用于确定结果向量的方向。与楔积不同，叉积的结果并不在高维空间中有直接的对应。

2. 结果的性质：

• 楔积的结果 是一种代表有向面积的几何对象，称为 2-形式，在三维空间中它不直接等同于一个向量，但与由原向量构成的平面有关。
• 叉积的结果 是一个向量，这个向量自身有长度和方向，其长度可以代表原来两个向量形成的平行四边形的面积，方向垂直于这两个向量构成的平面，根据右手规则确定。

3. 应用领域：

• 楔积 在数学中的应用范围更广，特别是在微分几何、代数拓扑和物理中的某些领域，如电磁学和流体动力学。楔积用于定义和计算多维空间中的有向体积元素。
• 叉积 主要用于三维几何和物理学中，如用于计算力的矩、角动量以及在三维空间中寻找垂直于两个给定向量的向量。

3. 外积、张量积

外积（outer product），在线性代数中一般指两个向量的 张量积，其结果为一 矩阵；与外积相对，两向量的内积结果为 标量。

外积是一种 克罗内克积 的特殊情况，给定 $m\times 1$ 列向量 $\mathbf{a}$ 和 $1\times n$ 行向量 $\mathbf{b}$，它们的外积 $\mathbf{a}\otimes \mathbf{b}$ 被定义为 $m\times n$ 矩阵 $\mathbf{C}$，结果为：

$$\mathbf{a}\otimes \mathbf{b}=\mathbf{C}=\mathbf{ab}$$

这里的外积即为张量积，张量积就是向量的乘法，使用坐标表示如下：

$$\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\\ b_4\end{array}\right]\otimes \left[\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right]=\left[\begin{array}{ccc}{a}_1{b}_1& a_2{b}_1& a_3{b}_1\\ a_1{b}_2& a_2{b}_2& a_3{b}_2\\ a_1{b}_3& a_2{b}_3& a_3{b}_3\\ a_1{b}_4& a_2{b}_4& a_3{b}_4\end{array}\right]$$

外积是将结果的维度扩张到二维，而内积呢，其结果将维度缩减到了标量。

4. 补充：克罗内克积

数学上，克罗内克积是两个任意大小的矩阵间的运算。克罗内克积是张量积的特殊（拓展）形式，以德国数学家利奥波德·克罗内克命名。

$\mathbf{A}\otimes \mathbf{B}$，如果 $\mathbf{A}$ 是一个 $m\times n$ 的矩阵，而 $\mathbf{B}$ 是一个 $p\times q$ 的矩阵，克罗内克积则是一个 $mp\times nq$ 的分块矩阵

$$\mathbf{A}\otimes \mathbf{B}=\left[\begin{array}{ccc}{a}_{11}\mathbf{B}& \cdots & a_{1n}\mathbf{B}\\ ⋮& \ddots & ⋮\\ a_{m1}\mathbf{B}& \cdots & a_{mn}\mathbf{B}\end{array}\right]$$

更具体而言：

$$\mathbf{A}\otimes \mathbf{B}=\left[\begin{array}{cccccccccc}{a}_{11}{b}_{11}& a_{11}{b}_{12}& \cdots & a_{11}{b}_{1q}& \cdots & \cdots & a_{1n}{b}_{11}& a_{1n}{b}_{12}& \cdots & a_{1n}{b}_{1q}\\ a_{11}{b}_{21}& a_{11}{b}_{22}& \cdots & a_{11}{b}_{2q}& \cdots & \cdots & a_{1n}{b}_{21}& a_{1n}{b}_{22}& \cdots & a_{1n}{b}_{2q}\\ ⋮& ⋮& \ddots & ⋮& & & ⋮& ⋮& \ddots & ⋮\\ a_{11}{b}_{p1}& a_{11}{b}_{p2}& \cdots & a_{11}{b}_{pq}& \cdots & \cdots & a_{1n}{b}_{p1}& a_{1n}{b}_{p2}& \cdots & a_{1n}{b}_{pq}\\ ⋮& ⋮& & ⋮& \ddots & & ⋮& ⋮& & ⋮\\ ⋮& ⋮& & ⋮& & \ddots & ⋮& ⋮& & ⋮\\ a_{m1}{b}_{11}& a_{m1}{b}_{12}& \cdots & a_{m1}{b}_{1q}& \cdots & \cdots & a_{mn}{b}_{11}& a_{mn}{b}_{12}& \cdots & a_{mn}{b}_{1q}\\ a_{m1}{b}_{21}& a_{m1}{b}_{22}& \cdots & a_{m1}{b}_{2q}& \cdots & \cdots & a_{mn}{b}_{21}& a_{mn}{b}_{22}& \cdots & a_{mn}{b}_{2q}\\ ⋮& ⋮& \ddots & ⋮& & & ⋮& ⋮& \ddots & ⋮\\ a_{m1}{b}_{p1}& a_{m1}{b}_{p2}& \cdots & a_{m1}{b}_{pq}& \cdots & \cdots & a_{mn}{b}_{p1}& a_{mn}{b}_{p2}& \cdots & a_{mn}{b}_{pq}\end{array}\right]$$

例如：

$$\left[\begin{array}{cc}1& 2\\ 3& 1\end{array}\right]\otimes \left[\begin{array}{cc}0& 3\\ 2& 1\end{array}\right]=\left[\begin{array}{cccc}1\cdot 0& 1\cdot 3& 2\cdot 0& 2\cdot 3\\ 1\cdot 2& 1\cdot 1& 2\cdot 2& 2\cdot 1\\ 3\cdot 0& 3\cdot 3& 1\cdot 0& 1\cdot 3\\ 3\cdot 2& 3\cdot 1& 1\cdot 2& 1\cdot 1\end{array}\right]=\left[\begin{array}{cccc}0& 3& 0& 6\\ 2& 1& 4& 2\\ 0& 9& 0& 3\\ 6& 3& 2& 1\end{array}\right]$$

克罗内克积有很多矩阵乘法没有的性质，具体感兴趣可以自行搜索，百科记录都很全。

---

via：

• 向量点乘(即内积)和叉乘(即外积、向量积)区别与意义分析-优快云博客
  https://blog.youkuaiyun.com/Lu_gl/article/details/122330285

• 带你一次搞懂点积（内积）、叉积（外积）-优快云博客
  https://blog.youkuaiyun.com/apr15/article/details/106160407

  • 向量点乘（内积）和叉乘（外积、向量积）概念及几何意义解读-优快云博客
    https://blog.youkuaiyun.com/dcrmg/article/details/52416832

  • 向量运算与几何应用-优快云博客
    https://blog.youkuaiyun.com/pangshaohua/article/details/87915950

  • 点乘和叉乘的区别是什么？ - 知乎
    https://www.zhihu.com/question/21080171

  • 向量运算精讲-优快云博客
    https://blog.youkuaiyun.com/Warmth_Dream/article/details/108500551

  • 向量点乘（内积）和叉乘（外积、向量积）概念及几何意义_两个向量点乘有什么意义-优快云博客
    https://blog.youkuaiyun.com/minmindianzi/article/details/84820362

• 点积、叉积、内积、外积【汇总对比】-优快云博客
  https://blog.youkuaiyun.com/Dust_Evc/article/details/127502272

• 向量的内积与外积 - 知乎
  https://zhuanlan.zhihu.com/p/91342476

• 真一文搞懂：内积、外积及其衍生（内积：点积、数量积、标量积；外积：叉积、叉乘、向量积、张量积） - 知乎
  https://zhuanlan.zhihu.com/p/685184693

  1. 百度百科：克罗内克积、内积、外积、叉积
  2. 维基百科：Inner Product, Outer Product, Cross Product, Exterior Product
  3. 线性代数教材：《Linear Algebra with Applications》（Gilbert Strang）
  4. 泛函分析教材：《Functional Analysis》（Walter Rudin）