注:本文为 “泰勒展开式” 相关合辑。
略作重排,未全校去重。
如有内容异常,请看原文。
浅显易懂——泰勒展开式
SoHardToNamed 于 2018-06-02 21:44:32 发布
首次接触泰勒展开式时,往往会感到困惑。泰勒公式的形式如下:
f
(
x
)
=
∑
i
=
0
n
f
(
i
)
(
x
0
)
i
!
(
x
−
x
0
)
i
f(x)=\sum_{i=0}^{n} \frac{f^{(i)}\left(x_{0}\right)}{i !}\left(x-x_{0}\right)^{i}
f(x)=i=0∑ni!f(i)(x0)(x−x0)i
若要深入理解该公式,需还原其推导过程,首要问题是:泰勒为何要提出这一公式?
在泰勒所处的时代,数学界对简单函数的研究与应用已趋于成熟,但对于复杂函数(如 f ( x ) = sin ( x 2 ) ⋅ ln ( 1 + x ) 1 2 f(x)=\sin(x^2)\cdot\ln(1+x)^{\frac{1}{2}} f(x)=sin(x2)⋅ln(1+x)21)及无明确表达式的曲线,仅能通过代入自变量 x x x 求得函数值 y y y,难以进行进一步分析。因此,泰勒致力于将这类复杂函数转化为简单形式,以便研究与应用。
泰勒的推导思路
要简化复杂函数,可尝试将其转化为其他易于分析的表达式。以 f ( x ) = sin ( x 2 ) ⋅ ln ( 1 + x ) f(x)=\sin(x^2)\cdot\ln(1+x) f(x)=sin(x2)⋅ln(1+x) 为例,直接分析整体难以突破,故从局部入手:
- 单点分析:取函数在点 x 0 x_0 x0 处的函数值,可得 f ( x 0 ) = y 0 f(x_0)=y_0 f(x0)=y0,此时尚未显现明显规律。
- 邻域分析:扩大研究范围,考虑
x
0
x_0
x0 的邻域
(
x
0
−
Δ
x
,
x
0
+
Δ
x
)
(x_0-\Delta x, x_0+\Delta x)
(x0−Δx,x0+Δx)(其中
Δ
x
→
0
\Delta x \to 0
Δx→0)。根据微分近似,函数在该邻域内可表示为:
f ( x ) = y 0 + k ( x − x 0 ) f(x)=y_0 + k(x-x_0) f(x)=y0+k(x−x0)
其中 Δ x = x − x 0 \Delta x = x - x_0 Δx=x−x0, k = f ′ ( x 0 ) k = f'(x_0) k=f′(x0)(即函数在 x 0 x_0 x0 处的一阶导数)。
将 y 0 = f ( x 0 ) ( x − x 0 ) 0 y_0 = f(x_0)(x-x_0)^0 y0=f(x0)(x−x0)0(因 ( x − x 0 ) 0 = 1 (x-x_0)^0 = 1 (x−x0)0=1)代入上式,可改写为:
f ( x ) = f ( 0 ) ( x 0 ) ( x − x 0 ) 0 + f ( 1 ) ( x 0 ) ( x − x 0 ) 1 f(x)=f^{(0)}(x_0)(x-x_0)^0 + f^{(1)}(x_0)(x-x_0)^1 f(x)=f(0)(x0)(x−x0)0+f(1)(x0)(x−x0)1
(注: f ( 0 ) ( x 0 ) f^{(0)}(x_0) f(0)(x0) 表示函数在 x 0 x_0 x0 处的零阶导数,即函数值本身; f ( 1 ) ( x 0 ) f^{(1)}(x_0) f(1)(x0) 表示一阶导数)
基于此,泰勒提出猜想:函数是否可扩展为更高阶的多项式形式?即:
f ( x ) = ∑ i = 0 n f ( i ) ( x 0 ) ( x − x 0 ) i = f ( 0 ) ( x 0 ) ( x − x 0 ) 0 + f ( 1 ) ( x 0 ) ( x − x 0 ) 1 + f ( 2 ) ( x 0 ) ( x − x 0 ) 2 + ⋯ \begin{align*} f(x) & =\sum\limits_{i=0}^{n}{{{f}^{(i)}}}({{x}_{0}}){{(x-{{x}_{0}})}^{i}} \\ & ={{f}^{(0)}}({{x}_{0}}){{(x-{{x}_{0}})}^{0}}+{{f}^{(1)}}({{x}_{0}}){{(x-{{x}_{0}})}^{1}}+{{f}^{(2)}}({{x}_{0}}){{(x-{{x}_{0}})}^{2}}+\cdots \end{align*} f(x)=i=0∑nf(i)(x0)(x−x0)i=f(0)(x0)(x−x0)0+f(1)(x0)(x−x0)1+f(2)(x0)(x−x0)2+⋯
猜想验证与修正
为验证上述猜想,对多项式逐项求导分析:
1. 单项导数规律
先对函数求一阶导数进行验证:当 x → x 0 x \to x_0 x→x0 时, f ′ ( x ) = f ′ ( x 0 ) f'(x) = f'(x_0) f′(x)=f′(x0),此式成立。
继续对函数求二阶导数推测验证,当 x → x 0 x \to x_0 x→x0 时, f ′ ′ ( x ) = 2 f ′ ′ ( x 0 ) f''(x) = 2f''(x_0) f′′(x)=2f′′(x0),该推测不成立。
取多项式中的任意一项 f ( m ) ( x 0 ) ( x − x 0 ) m f^{(m)}(x_0)(x-x_0)^m f(m)(x0)(x−x0)m( m m m 为非负整数),对其逐阶求导:
- 一阶导数: m ⋅ f ( m ) ( x 0 ) ( x − x 0 ) m − 1 m \cdot f^{(m)}(x_0)(x-x_0)^{m-1} m⋅f(m)(x0)(x−x0)m−1(多一项系数 m m m);
- 二阶导数: m ( m − 1 ) ⋅ f ( m ) ( x 0 ) ( x − x 0 ) m − 2 m(m-1) \cdot f^{(m)}(x_0)(x-x_0)^{m-2} m(m−1)⋅f(m)(x0)(x−x0)m−2(多一项系数 m ( m − 1 ) m(m-1) m(m−1));
- ⋮ \vdots ⋮
- m m m 阶导数: m ! ⋅ f ( m ) ( x 0 ) m! \cdot f^{(m)}(x_0) m!⋅f(m)(x0)( m ! m! m! 为 m m m 的阶乘,即 m ! = m × ( m − 1 ) × ⋯ × 1 m! = m \times (m-1) \times \cdots \times 1 m!=m×(m−1)×⋯×1);
- m + 1 m+1 m+1 阶导数:因 m ! ⋅ f ( m ) ( x 0 ) m! \cdot f^{(m)}(x_0) m!⋅f(m)(x0) 为常数,其导数为 0 0 0。
2. 邻域内的导数特性
当 x → x 0 x \to x_0 x→x0 时, x − x 0 → 0 x - x_0 \to 0 x−x0→0,因此:
- 对 f ( m ) ( x 0 ) ( x − x 0 ) m f^{(m)}(x_0)(x-x_0)^m f(m)(x0)(x−x0)m 求 小于 m m m 阶 的导数时,结果中仍含 ( x − x 0 ) (x-x_0) (x−x0) 的正次幂,趋近于 0 0 0;
- 求 等于 m m m 阶 的导数时,结果为 m ! ⋅ f ( m ) ( x 0 ) m! \cdot f^{(m)}(x_0) m!⋅f(m)(x0)(非零常数);
- 求 大于 m m m 阶 的导数时,结果为 0 0 0。
3. 系数修正
对猜想的多项式 ∑ i = 0 n f ( i ) ( x 0 ) ( x − x 0 ) i \sum_{i=0}^{n} f^{(i)}(x_0)(x-x_0)^i ∑i=0nf(i)(x0)(x−x0)i 求 m m m 阶导数,结果为 m ! ⋅ f ( m ) ( x 0 ) m! \cdot f^{(m)}(x_0) m!⋅f(m)(x0)。但我们期望多项式在 x 0 x_0 x0 处的 m m m 阶导数等于原函数的 m m m 阶导数 f ( m ) ( x 0 ) f^{(m)}(x_0) f(m)(x0),因此需将多项式各项除以 m ! m! m! 以修正系数,即乘以 1 m ! \frac{1}{m!} m!1。
修正后,函数在
x
0
x_0
x0 的邻域
(
x
0
−
Δ
x
,
x
0
+
Δ
x
)
(x_0-\Delta x, x_0+\Delta x)
(x0−Δx,x0+Δx) 内的最终泰勒公式形式可表示为:
f
(
x
)
=
∑
i
=
0
n
f
(
i
)
(
x
0
)
i
!
(
x
−
x
0
)
i
,
x
∈
(
x
0
−
Δ
x
,
x
0
+
Δ
x
)
f(x)=\sum\limits_{i=0}^{n} \frac{f^{(i)}\left(x_{0}\right)}{i !}\left(x-x_{0}\right)^{i},x\in \left( {{x}_{0}}-\Delta x,{{x}_{0}}+\Delta x \right)
f(x)=i=0∑ni!f(i)(x0)(x−x0)i,x∈(x0−Δx,x0+Δx)
泰勒公式推导过程(通俗+本质详解)
weixin_39578197 于 2020-11-29 05:15:10 发布
一、泰勒公式的核心定义
泰勒公式(也称泰勒展开式)是利用函数在某点的信息(各阶导数值),描述其在该点邻域内取值的数学公式。
若函数 f ( x ) f(x) f(x) 足够平滑(即存在直至 n + 1 n+1 n+1 阶的导数),则在已知 f ( x ) f(x) f(x) 在点 x 0 x_0 x0 处各阶导数值的情况下,可构造一个多项式函数近似 f ( x ) f(x) f(x),进而求解该邻域内任意点的函数值。
二、泰勒公式的作用
用多项式函数逼近给定函数(即使多项式图像与原函数图像在某点邻域内拟合)。注意,逼近的时候一定是从函数图像上的某个点展开。
对于复杂函数(如无法直接计算某点值的函数),可通过泰勒公式构造多项式近似求解。在机器学习领域,泰勒公式主要应用于梯度迭代算法。
三、问题的提出:为何选择多项式逼近?
-
多项式函数的一般形式为:
P n ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n − 1 x n − 1 + a n x n P_n(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_{n-1} x^{n-1} + a_n x^n Pn(x)=a0+a1x+a2x2+⋯+an−1xn−1+anxn
其中 a 0 , a 1 , … , a n a_0, a_1, \dots, a_n a0,a1,…,an 为系数。 -
多项式函数的优势在于:对于任意给定的自变量取值,仅需通过有限次加法与乘法运算即可计算出对应的函数值,其数值计算过程具有效率高、逻辑清晰且易于编程实现或手工操作的特点。正是基于这一核心优势,泰勒公式选择多项式函数作为逼近复杂函数的工具——通过构造与复杂函数在局部具有近似函数值、各阶导数值的多项式函数,将难以直接分析和计算的复杂函数转化为结构简单的多项式函数,从而降低函数研究与数值计算的难度。
四、近似计算举例(以 f ( x ) = cos x f(x)=\cos x f(x)=cosx 为例)
初等数学中, x 5 \sqrt[5]{x} 5x、 e x e^x ex、 sin x \sin x sinx、 cos x \cos x cosx、 ln ( 1 + x ) \ln(1+x) ln(1+x)、 arctan x \arctan x arctanx 等函数精确计算困难,可通过多项式逼近简化。以下以 f ( x ) = cos x f(x)=\cos x f(x)=cosx 在 x 0 = 0 x_0 = 0 x0=0 附近的逼近展开说明:
1. 一次(线性)逼近
函数
f
(
x
)
f(x)
f(x) 在点
x
0
x_0
x0 附近的线性逼近公式(由导数与微分定义推导):
f
(
x
)
≈
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
f(x) \approx f(x_0) + f'(x_0)(x - x_0)
f(x)≈f(x0)+f′(x0)(x−x0)
当
x
0
=
0
x_0 = 0
x0=0 时,公式简化为:
f
(
x
)
≈
f
(
0
)
+
f
′
(
0
)
⋅
x
f(x) \approx f(0) + f'(0) \cdot x
f(x)≈f(0)+f′(0)⋅x
f ( x ) = cos x f(x) = \cos x f(x)=cosx 在 x 0 = 0 x_0 = 0 x0=0 处的一次(线性)逼近推导
-
计算基础量:
函数值: f ( 0 ) = cos 0 = 1 f(0) = \cos 0 = 1 f(0)=cos0=1;
一阶导数: f ′ ( x ) = − sin x f'(x) = -\sin x f′(x)=−sinx,故 f ′ ( 0 ) = − sin 0 = 0 f'(0) = -\sin 0 = 0 f′(0)=−sin0=0。
-
构造逼近多项式:
将基础量代入简化公式,得:
cos x ≈ 1 + 0 ⋅ x = 1 \cos x \approx 1 + 0 \cdot x = 1 cosx≈1+0⋅x=1
因此, f ( x ) = cos x f(x) = \cos x f(x)=cosx 在 x 0 = 0 x_0 = 0 x0=0 附近的一次(线性)逼近多项式为:
P 1 ( x ) = 1 P_1(x) = 1 P1(x)=1
特点
P 1 ( x ) = 1 P_1(x) = 1 P1(x)=1 形式简单、计算便捷,但精度低。因仅反映 x 0 = 0 x_0 = 0 x0=0 处局部线性特性, x x x 远离 0 0 0 时,误差显著增大。
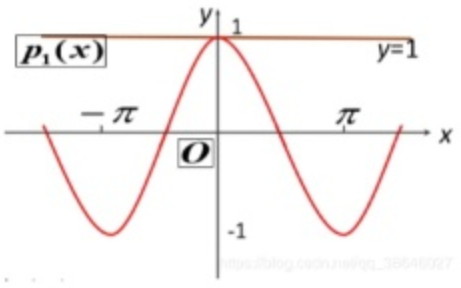
几何意义: P 1 ( x ) = 1 P_1(x) = 1 P1(x)=1 是 y = cos x y = \cos x y=cosx 在 ( 0 , 1 ) (0, 1) (0,1) 处的切线,仅在该点附近与原函数图像贴合。
② 二次逼近:构造多项式与多阶导数匹配
为实现对 f ( x ) = cos x f(x) = \cos x f(x)=cosx 的局部逼近,构造二次多项式 P 2 ( x ) = a 0 + a 1 x + a 2 x 2 P_2(x) = a_0 + a_1 x + a_2 x^2 P2(x)=a0+a1x+a2x2 。我们要求 P 2 ( x ) P_2(x) P2(x) 与 f ( x ) f(x) f(x) 在 x 0 = 0 x_0 = 0 x0=0 处满足 “函数值、一阶导数、二阶导数逐层匹配” 的条件,以此保证两者在该点邻域内的局部形态一致性(从函数值到斜率,再到曲率的逐步拟合 )。
1. 零阶匹配:函数值相等(常数项确定)
要求
P
2
(
x
)
P_2(x)
P2(x) 与
f
(
x
)
f(x)
f(x) 在
x
=
0
x = 0
x=0 处函数值相等,即:
P
2
(
0
)
=
f
(
0
)
P_2(0) = f(0)
P2(0)=f(0)
-
代入多项式与原函数:
P 2 ( 0 ) = a 0 + a 1 ⋅ 0 + a 2 ⋅ 0 2 = a 0 P_2(0) = a_0 + a_1 \cdot 0 + a_2 \cdot 0^2 = a_0 P2(0)=a0+a1⋅0+a2⋅02=a0,
f ( 0 ) = cos 0 = 1 f(0) = \cos 0 = 1 f(0)=cos0=1。 -
结论:由 a 0 = 1 a_0 = 1 a0=1,确定二次多项式的常数项 a 0 = 1 a_0 = 1 a0=1 。
2. 一阶匹配:一阶导数相等(一次项系数确定)
要求
P
2
(
x
)
P_2(x)
P2(x) 与
f
(
x
)
f(x)
f(x) 在
x
=
0
x = 0
x=0 处一阶导数值相等(即切线斜率相同),即:
P
2
′
(
0
)
=
f
′
(
0
)
P_2'(0) = f'(0)
P2′(0)=f′(0)
-
先求导:
P 2 ′ ( x ) = a 1 + 2 a 2 x P_2'(x) = a_1 + 2a_2 x P2′(x)=a1+2a2x,故 P 2 ′ ( 0 ) = a 1 P_2'(0) = a_1 P2′(0)=a1;
f ′ ( x ) = − sin x f'(x) = -\sin x f′(x)=−sinx,故 f ′ ( 0 ) = − sin 0 = 0 f'(0) = -\sin 0 = 0 f′(0)=−sin0=0。 -
结论:由 a 1 = 0 a_1 = 0 a1=0,确定二次多项式的一次项系数 a 1 = 0 a_1 = 0 a1=0 。
3. 二阶匹配:二阶导数相等(二次项系数确定)
要求
P
2
(
x
)
P_2(x)
P2(x) 与
f
(
x
)
f(x)
f(x) 在
x
=
0
x = 0
x=0 处二阶导数值相等(即曲线弯曲程度与方向相同 ),即:
P
2
′
′
(
0
)
=
f
′
′
(
0
)
P_2''(0) = f''(0)
P2′′(0)=f′′(0)
-
再求导:
P 2 ′ ′ ( x ) = 2 a 2 P_2''(x) = 2a_2 P2′′(x)=2a2,故 P 2 ′ ′ ( 0 ) = 2 a 2 P_2''(0) = 2a_2 P2′′(0)=2a2;
f ′ ′ ( x ) = − cos x f''(x) = -\cos x f′′(x)=−cosx,故 f ′ ′ ( 0 ) = − cos 0 = − 1 f''(0) = -\cos 0 = -1 f′′(0)=−cos0=−1。 -
结论:由 2 a 2 = − 1 2a_2 = -1 2a2=−1,解得二次多项式的二次项系数 a 2 = − 1 2 a_2 = -\frac{1}{2} a2=−21 。
4. 二次逼近多项式与结论
将
a
0
=
1
a_0 = 1
a0=1、
a
1
=
0
a_1 = 0
a1=0、
a
2
=
−
1
2
a_2 = -\frac{1}{2}
a2=−21 代入
P
2
(
x
)
P_2(x)
P2(x),得到
f
(
x
)
=
cos
x
f(x) = \cos x
f(x)=cosx 在
x
0
=
0
x_0 = 0
x0=0 附近的二次逼近多项式:
P
2
(
x
)
=
1
−
1
2
x
2
P_2(x) = 1 - \frac{1}{2}x^2
P2(x)=1−21x2
因此,在
x
0
=
0
x_0 = 0
x0=0 的邻域内,可近似表示为:
cos
x
≈
P
2
(
x
)
=
1
−
1
2
x
2
\cos x \approx P_2(x) = 1 - \frac{1}{2}x^2
cosx≈P2(x)=1−21x2
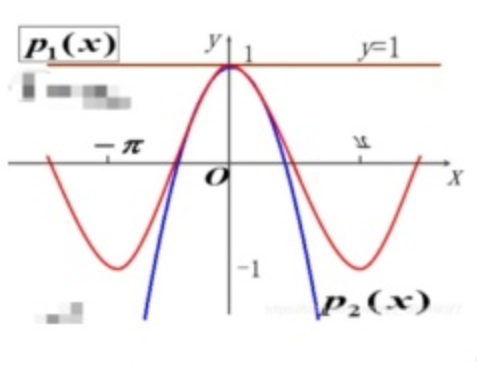
几何意义与适用范围
从几何角度看, P 2 ( x ) P_2(x) P2(x) 与 cos x \cos x cosx 在 ( 0 , 1 ) (0, 1) (0,1) 处实现了**“函数值、切线斜率、曲率”的三重匹配**,其逼近效果优于一次线性逼近。但需注意:
- 该逼近仅在局部区间(如 [ − π 2 , π 2 ] [-\frac{\pi}{2}, \frac{\pi}{2}] [−2π,2π] 附近 )具备较好拟合度;
- 当 x x x 远离 x 0 = 0 x_0 = 0 x0=0 时,误差会显著增大(因多项式仅能局部模拟原函数的非线性特征)。
3. 八次逼近
构造八次多项式 P 8 ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a 8 x 8 P_8(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_8 x^8 P8(x)=a0+a1x+a2x2+⋯+a8x8,要求其与 f ( x ) = cos x f(x)=\cos x f(x)=cosx 在 x 0 = 0 x_0=0 x0=0 处满足 函数值、一阶至八阶导数值均相等:
- P 8 ( 0 ) = f ( 0 ) = 1 ⟹ a 0 = 1 P_8(0) = f(0) = 1 \implies a_0 = 1 P8(0)=f(0)=1⟹a0=1;
- P 8 ′ ( 0 ) = f ′ ( 0 ) = 0 ⟹ a 1 = 0 P_8'(0) = f'(0) = 0 \implies a_1 = 0 P8′(0)=f′(0)=0⟹a1=0;
- P 8 ′ ′ ( 0 ) = f ′ ′ ( 0 ) = − 1 ⟹ 2 ! a 2 = − 1 ⟹ a 2 = − 1 2 ! P_8''(0) = f''(0) = -1 \implies 2!a_2 = -1 \implies a_2 = -\frac{1}{2!} P8′′(0)=f′′(0)=−1⟹2!a2=−1⟹a2=−2!1;
- P 8 ′ ′ ′ ( 0 ) = f ′ ′ ′ ( 0 ) = 0 ⟹ 3 ! a 3 = 0 ⟹ a 3 = 0 P_8'''(0) = f'''(0) = 0 \implies 3!a_3 = 0 \implies a_3 = 0 P8′′′(0)=f′′′(0)=0⟹3!a3=0⟹a3=0;
- P 8 ( 4 ) ( 0 ) = f ( 4 ) ( 0 ) = 1 ⟹ 4 ! a 4 = 1 ⟹ a 4 = 1 4 ! P_8^{(4)}(0) = f^{(4)}(0) = 1 \implies 4!a_4 = 1 \implies a_4 = \frac{1}{4!} P8(4)(0)=f(4)(0)=1⟹4!a4=1⟹a4=4!1;
- ⋮ \vdots ⋮
- P 8 ( 8 ) ( 0 ) = f ( 8 ) ( 0 ) = 1 ⟹ 8 ! a 8 = 1 ⟹ a 8 = 1 8 ! P_8^{(8)}(0) = f^{(8)}(0) = 1 \implies 8!a_8 = 1 \implies a_8 = \frac{1}{8!} P8(8)(0)=f(8)(0)=1⟹8!a8=1⟹a8=8!1。
最终得到八次逼近多项式:
P
8
(
x
)
=
1
−
1
2
!
x
2
+
1
4
!
x
4
−
1
6
!
x
6
+
1
8
!
x
8
P_8(x) = 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - \frac{1}{6!}x^6 + \frac{1}{8!}x^8
P8(x)=1−2!1x2+4!1x4−6!1x6+8!1x8
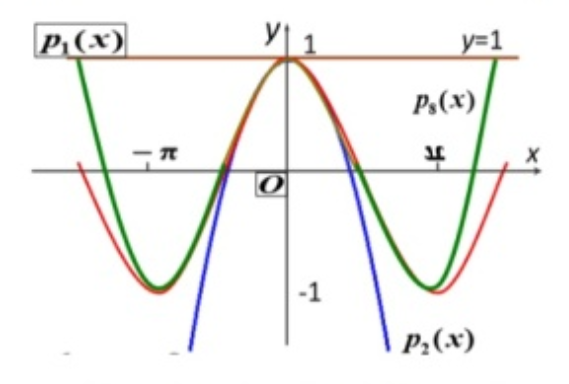
特点: P 8 ( x ) P_8(x) P8(x)(绿色图像)比 P 2 ( x ) P_2(x) P2(x)(蓝色图像)在更大范围内接近 cos x \cos x cosx(红色图像)。
综上,当对精度要求较高或需估计误差时,需采用高次多项式逼近,并引入误差公式量化偏差。
五、泰勒公式的推导
1. 定义问题
给定函数
f
(
x
)
f(x)
f(x),寻找一个在
x
0
x_0
x0 附近与
f
(
x
)
f(x)
f(x) 近似的
n
n
n 次多项式
P
n
(
x
)
P_n(x)
Pn(x),满足:
P
n
(
x
)
=
a
0
+
a
1
(
x
−
x
0
)
+
a
2
(
x
−
x
0
)
2
+
⋯
+
a
n
(
x
−
x
0
)
n
P_n(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)^2 + \cdots + a_n(x-x_0)^n
Pn(x)=a0+a1(x−x0)+a2(x−x0)2+⋯+an(x−x0)n
使得
f
(
x
)
≈
P
n
(
x
)
f(x) \approx P_n(x)
f(x)≈Pn(x) 并且两者误差
R
n
(
x
)
=
f
(
x
)
−
P
n
(
x
)
R_n(x) = f(x) - P_n(x)
Rn(x)=f(x)−Pn(x) 可估计。
误差 R n ( x ) R_n(x) Rn(x) 量化了 f ( x ) f(x) f(x) 与 P n ( x ) P_n(x) Pn(x) 在 x 0 x_0 x0 附近的偏差。理想情况下,误差应尽可能小,以确保 P n ( x ) P_n(x) Pn(x) 精确逼近 f ( x ) f(x) f(x)。
几何解释:图中 y = f ( x ) y = f(x) y=f(x) 和 y = P n ( x ) y = P_n(x) y=Pn(x) 为两条曲线,展示了 P n ( x ) P_n(x) Pn(x) 对 f ( x ) f(x) f(x) 的逼近效果。
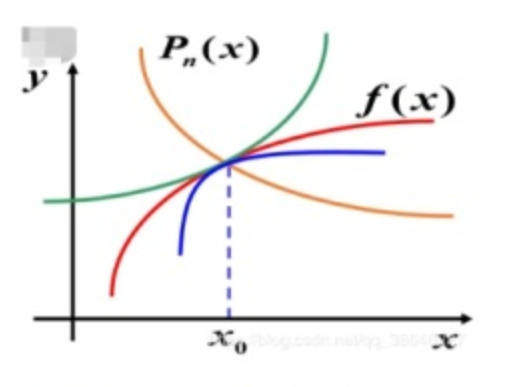
2. 多项式的约束条件
从几何角度, y = f ( x ) y = f(x) y=f(x) 与 y = P n ( x ) y = P_n(x) y=Pn(x) 的图像需在 x 0 x_0 x0 附近充分接近,因此需满足以下条件:
- 相交:两曲线在点 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0)) 相交,即 P n ( x 0 ) = f ( x 0 ) P_n(x_0) = f(x_0) Pn(x0)=f(x0);
- 相切:两曲线在点 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0)) 斜率相同,即 P n ′ ( x 0 ) = f ′ ( x 0 ) P_n'(x_0) = f'(x_0) Pn′(x0)=f′(x0);
- 曲率一致:两曲线在点 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0)) 弯曲方向相同,即 P n ′ ′ ( x 0 ) = f ′ ′ ( x 0 ) P_n''(x_0) = f''(x_0) Pn′′(x0)=f′′(x0);
- 高阶拟合:进一步提高精度,要求直至 n n n 阶导数值均相等,即 P n ( k ) ( x 0 ) = f ( k ) ( x 0 ) P_n^{(k)}(x_0) = f^{(k)}(x_0) Pn(k)(x0)=f(k)(x0)( k = 0 , 1 , 2 , … , n k = 0, 1, 2, \dots, n k=0,1,2,…,n)。
3. 多项式系数的求解
对 P n ( x ) P_n(x) Pn(x) 逐阶求导,并代入 x = x 0 x = x_0 x=x0,结合约束条件求解系数 a k a_k ak:
- 零阶导数(函数值): P n ( x 0 ) = a 0 = f ( x 0 ) ⟹ a 0 = f ( x 0 ) P_n(x_0) = a_0 = f(x_0) \implies a_0 = f(x_0) Pn(x0)=a0=f(x0)⟹a0=f(x0);
- 一阶导数: P n ′ ( x ) = a 1 + 2 a 2 ( x − x 0 ) + ⋯ + n a n ( x − x 0 ) n − 1 P_n'(x) = a_1 + 2a_2(x-x_0) + \cdots + na_n(x-x_0)^{n-1} Pn′(x)=a1+2a2(x−x0)+⋯+nan(x−x0)n−1,代入 x = x 0 x = x_0 x=x0 得 P n ′ ( x 0 ) = a 1 = f ′ ( x 0 ) ⟹ a 1 = f ′ ( x 0 ) P_n'(x_0) = a_1 = f'(x_0) \implies a_1 = f'(x_0) Pn′(x0)=a1=f′(x0)⟹a1=f′(x0);
- 二阶导数: P n ′ ′ ( x ) = 2 a 2 + 3 × 2 a 3 ( x − x 0 ) + ⋯ + n ( n − 1 ) a n ( x − x 0 ) n − 2 P_n''(x) = 2a_2 + 3 \times 2a_3(x-x_0) + \cdots + n(n-1)a_n(x-x_0)^{n-2} Pn′′(x)=2a2+3×2a3(x−x0)+⋯+n(n−1)an(x−x0)n−2,代入 x = x 0 x = x_0 x=x0 得 P n ′ ′ ( x 0 ) = 2 ! a 2 = f ′ ′ ( x 0 ) ⟹ a 2 = f ′ ′ ( x 0 ) 2 ! P_n''(x_0) = 2!a_2 = f''(x_0) \implies a_2 = \frac{f''(x_0)}{2!} Pn′′(x0)=2!a2=f′′(x0)⟹a2=2!f′′(x0);
- ⋮ \vdots ⋮
- k k k 阶导数: P n ( k ) ( x 0 ) = k ! a k = f ( k ) ( x 0 ) ⟹ a k = f ( k ) ( x 0 ) k ! P_n^{(k)}(x_0) = k!a_k = f^{(k)}(x_0) \implies a_k = \frac{f^{(k)}(x_0)}{k!} Pn(k)(x0)=k!ak=f(k)(x0)⟹ak=k!f(k)(x0)( k = 0 , 1 , … , n k = 0, 1, \dots, n k=0,1,…,n)。
4. 泰勒多项式与误差
将系数
a
k
a_k
ak 代入
P
n
(
x
)
P_n(x)
Pn(x),得到 泰勒多项式:
P
n
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
f
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
⋯
+
f
(
n
)
(
x
0
)
n
!
(
x
−
x
0
)
n
P_n(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n
Pn(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯+n!f(n)(x0)(x−x0)n
函数
f
(
x
)
f(x)
f(x) 与泰勒多项式
P
n
(
x
)
P_n(x)
Pn(x) 的差值即为 误差(余项):
R
n
(
x
)
=
f
(
x
)
−
P
n
(
x
)
R_n(x) = f(x) - P_n(x)
Rn(x)=f(x)−Pn(x)
六、泰勒公式的定义
若函数
f
(
x
)
f(x)
f(x) 在包含
x
0
x_0
x0 的开区间
(
a
,
b
)
(a, b)
(a,b) 内具有直至
n
+
1
n+1
n+1 阶的导数,则对任意
x
∈
(
a
,
b
)
x \in (a, b)
x∈(a,b),有:
f
(
x
)
=
f
(
x
0
)
0
!
+
f
′
(
x
0
)
1
!
(
x
−
x
0
)
+
f
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
⋯
+
f
(
n
)
(
x
0
)
n
!
(
x
−
x
0
)
n
+
R
n
(
x
)
f(x) = \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)
f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯+n!f(n)(x0)(x−x0)n+Rn(x)
其中,
R
n
(
x
)
R_n(x)
Rn(x) 为 拉格朗日余项(误差项),表达式为:
R
n
(
x
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
x
0
)
n
+
1
R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}
Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1
(
ξ
\xi
ξ 为
x
0
x_0
x0 与
x
x
x 之间的某个数)
拉格朗日余项的本质是将泰勒多项式扩展至 n + 1 n+1 n+1 阶,通过更高阶的导数量化逼近误差。
七、扩展:麦克劳林公式
麦克劳林公式是泰勒公式的 特殊情况,即当
x
0
=
0
x_0 = 0
x0=0 时的泰勒展开式。将
x
0
=
0
x_0 = 0
x0=0 代入泰勒公式,得:
f
(
x
)
=
f
(
0
)
0
!
+
f
′
(
0
)
1
!
x
+
f
′
′
(
0
)
2
!
x
2
+
⋯
+
f
(
n
)
(
0
)
n
!
x
n
+
R
n
(
x
)
f(x) = \frac{f(0)}{0!} + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2 + \cdots + \frac{f^{(n)}(0)}{n!}x^n + R_n(x)
f(x)=0!f(0)+1!f′(0)x+2!f′′(0)x2+⋯+n!f(n)(0)xn+Rn(x)
常见初等函数的麦克劳林公式(带佩亚诺余项)
佩亚诺余项的形式为 R n ( x ) = o [ ( x − x 0 ) n ] R_n(x) = o[(x-x_0)^n] Rn(x)=o[(x−x0)n](即 ( x − x 0 ) n (x-x_0)^n (x−x0)n 的高阶无穷小),当 x 0 = 0 x_0 = 0 x0=0 时,余项为 o ( x n ) o(x^n) o(xn)。
以下是几个常用函数的麦克劳林展开:
-
指数函数:
e x = 1 + x + 1 2 ! x 2 + ⋯ + 1 n ! x n + o ( x n ) e^x = 1 + x + \frac{1}{2!}x^2 + \cdots + \frac{1}{n!}x^n + o(x^n) ex=1+x+2!1x2+⋯+n!1xn+o(xn) -
正弦函数:
sin x = x − 1 3 ! x 3 + ⋯ + ( − 1 ) m − 1 ( 2 m − 1 ) ! x 2 m − 1 + o ( x 2 m − 1 ) \sin x = x - \frac{1}{3!}x^3 + \cdots + \frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1} + o(x^{2m-1}) sinx=x−3!1x3+⋯+(2m−1)!(−1)m−1x2m−1+o(x2m−1) -
余弦函数:
cos x = 1 − 1 2 ! x 2 + 1 4 ! x 4 − ⋯ + ( − 1 ) m ( 2 m ) ! x 2 m + o ( x 2 m ) \cos x = 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - \cdots + \frac{(-1)^m}{(2m)!}x^{2m} + o(x^{2m}) cosx=1−2!1x2+4!1x4−⋯+(2m)!(−1)mx2m+o(x2m) -
对数函数:
ln ( 1 + x ) = x − 1 2 x 2 + 1 3 x 3 − ⋯ + ( − 1 ) n − 1 n x n + o ( x n ) \ln(1+x) = x - \frac{1}{2}x^2 + \frac{1}{3}x^3 - \cdots + \frac{(-1)^{n-1}}{n}x^n + o(x^n) ln(1+x)=x−21x2+31x3−⋯+n(−1)n−1xn+o(xn)
泰勒公式的余项、性质、特殊形式及应用
一、泰勒公式的余项形式
在泰勒公式中,余项用于量化多项式对原函数的逼近误差,主要有以下两种形式,适用场景各有不同:
1. 拉格朗日余项
若函数
f
(
x
)
f(x)
f(x) 在包含
x
0
x_0
x0 的开区间
(
a
,
b
)
(a,b)
(a,b) 内存在
n
+
1
n+1
n+1 阶导数,则拉格朗日余项可表示为:
R
n
(
x
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
x
0
)
n
+
1
R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}
Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1
其中
ξ
\xi
ξ 是介于
x
0
x_0
x0 与
x
x
x 之间的数。
特点与应用:
- 优势:可定量估计误差,适用于需严格控制精度的场景(如数值计算的精度验证 )。
- 示例:用 n n n 次泰勒多项式逼近 f ( x ) = sin x f(x)=\sin x f(x)=sinx 时,通过拉格朗日余项可计算 x ∈ [ − 1 , 1 ] x \in [-1,1] x∈[−1,1] 内的最大误差,确保结果满足精度要求。
2. 佩亚诺余项
佩亚诺余项的形式为:
R
n
(
x
)
=
o
[
(
x
−
x
0
)
n
]
R_n(x) = o\left[(x-x_0)^n\right]
Rn(x)=o[(x−x0)n]
其中
o
[
(
x
−
x
0
)
n
]
o\left[(x-x_0)^n\right]
o[(x−x0)n] 表示当
x
→
x
0
x \to x_0
x→x0 时,余项是
(
x
−
x
0
)
n
(x-x_0)^n
(x−x0)n 的高阶无穷小(余项趋于0的速度快于
(
x
−
x
0
)
n
(x-x_0)^n
(x−x0)n )。
特点与应用:
- 优势:形式简洁,无需考虑 n + 1 n+1 n+1 阶导数的具体值,适用于分析函数在 x 0 x_0 x0 附近的局部逼近性质(如求极限、判断极值 )。
- 示例:计算 lim x → 0 sin x − x x 3 \lim\limits_{x \to 0} \frac{\sin x - x}{x^3} x→0limx3sinx−x 时,利用 sin x \sin x sinx 的麦克劳林展开(带佩亚诺余项) sin x = x − 1 3 ! x 3 + o ( x 3 ) \sin x = x - \frac{1}{3!}x^3 + o(x^3) sinx=x−3!1x3+o(x3),可快速化简得极限为 − 1 6 -\frac{1}{6} −61。
二、泰勒公式的核心性质
1. 逼近的“局部性”
泰勒公式的逼近效果集中体现于 x 0 x_0 x0 的邻域(即 x x x 与 x 0 x_0 x0 足够接近时 )。即使是高次多项式,当 x x x 远离 x 0 x_0 x0 时,误差会显著增大。
示例: f ( x ) = cos x f(x)=\cos x f(x)=cosx 在 x 0 = 0 x_0=0 x0=0 处的八次麦克劳林多项式 P 8 ( x ) P_8(x) P8(x),在 x ∈ [ − π , π ] x \in [-\pi, \pi] x∈[−π,π] 内与 cos x \cos x cosx 拟合较好;但当 x > π x > \pi x>π 或 x < − π x < -\pi x<−π 时, P 8 ( x ) P_8(x) P8(x) 会快速偏离真实值,印证了“局部性”特征。
2. 导数的“信息传递”
泰勒公式的本质是将函数 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处的各阶导数信息转化为多项式系数,通过多项式“复现”函数的局部性质。导数阶数越高,多项式包含的函数信息越丰富,逼近精度越高(邻域内 )。
示例:
- 零阶多项式 P 0 ( x ) = f ( x 0 ) P_0(x)=f(x_0) P0(x)=f(x0):仅利用函数值,是“常数逼近”;
- 一阶多项式 P 1 ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) P_1(x)=f(x_0)+f'(x_0)(x-x_0) P1(x)=f(x0)+f′(x0)(x−x0):利用函数值与一阶导数,是“线性逼近”;
- 二阶多项式:额外利用二阶导数,实现“曲率匹配”,逼近效果进一步提升。
三、麦克劳林公式的价值与应用
麦克劳林公式是 x 0 = 0 x_0=0 x0=0 时的泰勒公式,因展开点简单,在工程计算、物理建模中应用广泛:
1. 简化复杂函数计算
对于无法直接计算的函数值(如 e 0.1 e^{0.1} e0.1、 sin 0.05 \sin 0.05 sin0.05 ),可通过麦克劳林展开的前几项快速估算。
示例:计算
e
0.1
e^{0.1}
e0.1 时,利用
e
x
e^x
ex 的麦克劳林公式:
e
x
=
1
+
x
+
1
2
!
x
2
+
1
3
!
x
3
+
o
(
x
3
)
e^x = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + o(x^3)
ex=1+x+2!1x2+3!1x3+o(x3)
代入
x
=
0.1
x=0.1
x=0.1,取前4项计算:
e
0.1
≈
1
+
0.1
+
1
2
×
0.1
2
+
1
6
×
0.1
3
=
1.105166
⋯
e^{0.1} \approx 1 + 0.1 + \frac{1}{2} \times 0.1^2 + \frac{1}{6} \times 0.1^3 = 1.105166\cdots
e0.1≈1+0.1+21×0.12+61×0.13=1.105166⋯
与真实值
e
0.1
≈
1.105170918
e^{0.1} \approx 1.105170918
e0.1≈1.105170918 的误差约
4.3
×
10
−
6
4.3 \times 10^{-6}
4.3×10−6,满足工程精度需求。
2. 推导函数的运算公式
利用麦克劳林公式可简化函数的乘积、商、复合等运算。
示例:推导 e x ⋅ sin x e^x \cdot \sin x ex⋅sinx 的麦克劳林展开式(前3项 ):
- 已知 e x = 1 + x + 1 2 ! x 2 + o ( x 2 ) e^x = 1 + x + \frac{1}{2!}x^2 + o(x^2) ex=1+x+2!1x2+o(x2), sin x = x − 1 3 ! x 3 + o ( x 3 ) \sin x = x - \frac{1}{3!}x^3 + o(x^3) sinx=x−3!1x3+o(x3);
- 相乘时忽略高于
x
3
x^3
x3 的项(佩亚诺余项吸收高阶无穷小 ):
e x ⋅ sin x = ( 1 + x + 1 2 x 2 ) ( x − 1 6 x 3 ) + o ( x 3 ) = x + x 2 + 1 3 x 3 + o ( x 3 ) \begin{align*} e^x \cdot \sin x &= \left(1 + x + \frac{1}{2}x^2\right)\left(x - \frac{1}{6}x^3\right) + o(x^3) \\ &= x + x^2 + \frac{1}{3}x^3 + o(x^3) \end{align*} ex⋅sinx=(1+x+21x2)(x−61x3)+o(x3)=x+x2+31x3+o(x3)
该结果可用于极限计算或积分近似。
四、泰勒公式在数值分析中的应用
1. 数值积分
对于无法用初等函数表示原函数的积分(如 ∫ 0 1 e − x 2 d x \int_0^1 e^{-x^2}dx ∫01e−x2dx ),可先将被积函数展开为泰勒多项式,再积分实现“近似计算”。
示例:计算 ∫ 0 0.5 cos x 2 d x \int_0^{0.5} \cos x^2 dx ∫00.5cosx2dx:
- 利用 cos t \cos t cost 的麦克劳林公式(令 t = x 2 t=x^2 t=x2 ): cos x 2 = 1 − 1 2 ! x 4 + 1 4 ! x 8 − o ( x 8 ) \cos x^2 = 1 - \frac{1}{2!}x^4 + \frac{1}{4!}x^8 - o(x^8) cosx2=1−2!1x4+4!1x8−o(x8);
- 对多项式积分:
∫ 0 0.5 cos x 2 d x ≈ ∫ 0 0.5 ( 1 − 1 2 x 4 + 1 24 x 8 ) d x = [ x − 1 10 x 5 + 1 216 x 9 ] 0 0.5 ≈ 0.499583 \begin{align*} \int_0^{0.5} \cos x^2 dx &\approx \int_0^{0.5} \left(1 - \frac{1}{2}x^4 + \frac{1}{24}x^8\right)dx \\ &= \left[ x - \frac{1}{10}x^5 + \frac{1}{216}x^9 \right]_0^{0.5} \\ & \approx 0.499583 \end{align*} ∫00.5cosx2dx≈∫00.5(1−21x4+241x8)dx=[x−101x5+2161x9]00.5≈0.499583
与辛普森法计算的精确值(约 0.499583)基本一致。
2. 方程求根(牛顿迭代法)
牛顿迭代法是常用的方程求根算法,其核心理论基于泰勒公式。
原理:
对于方程
f
(
x
)
=
0
f(x)=0
f(x)=0,取
x
0
x_0
x0 为初始近似根,将
f
(
x
)
f(x)
f(x) 在
x
0
x_0
x0 处展开为一阶泰勒多项式:
f
(
x
)
≈
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
f(x) \approx f(x_0) + f'(x_0)(x - x_0)
f(x)≈f(x0)+f′(x0)(x−x0)
令多项式为 0,解出下一个近似根:
x
1
=
x
0
−
f
(
x
0
)
f
′
(
x
0
)
x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}
x1=x0−f′(x0)f(x0)
重复过程直至满足精度要求。牛顿迭代法的快速收敛性,源于一阶泰勒多项式对
f
(
x
)
f(x)
f(x) 的局部逼近效果。
via:
-
浅显易懂 —— 泰勒展开式 - 优快云 博客
https://blog.youkuaiyun.com/SoHardToNamed/article/details/80550935 -
泰勒公式推导过程_Taylor 公式(泰勒公式)通俗 + 本质详解 - 优快云 博客
https://blog.youkuaiyun.com/weixin_39578197/article/details/110866791 -
泰勒展开续集 —— 拉格朗日余项如何推导?有何含义?_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV12s411E7nv/





















 8102
8102

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








