磁路 | 概念 / 定律 / 定理

注：本文为 “磁路” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未全校去重。
如有内容异常，请看原文。

---

磁路基本定律

吮指原味张 于 2021-07-24 10:12:27 发布

参考资料

《电机学 第五版》_汤蕴璆_第1章 磁路_1.1 磁路的基本定律

1. 磁路的概念

磁通所通过的路径称为磁路。

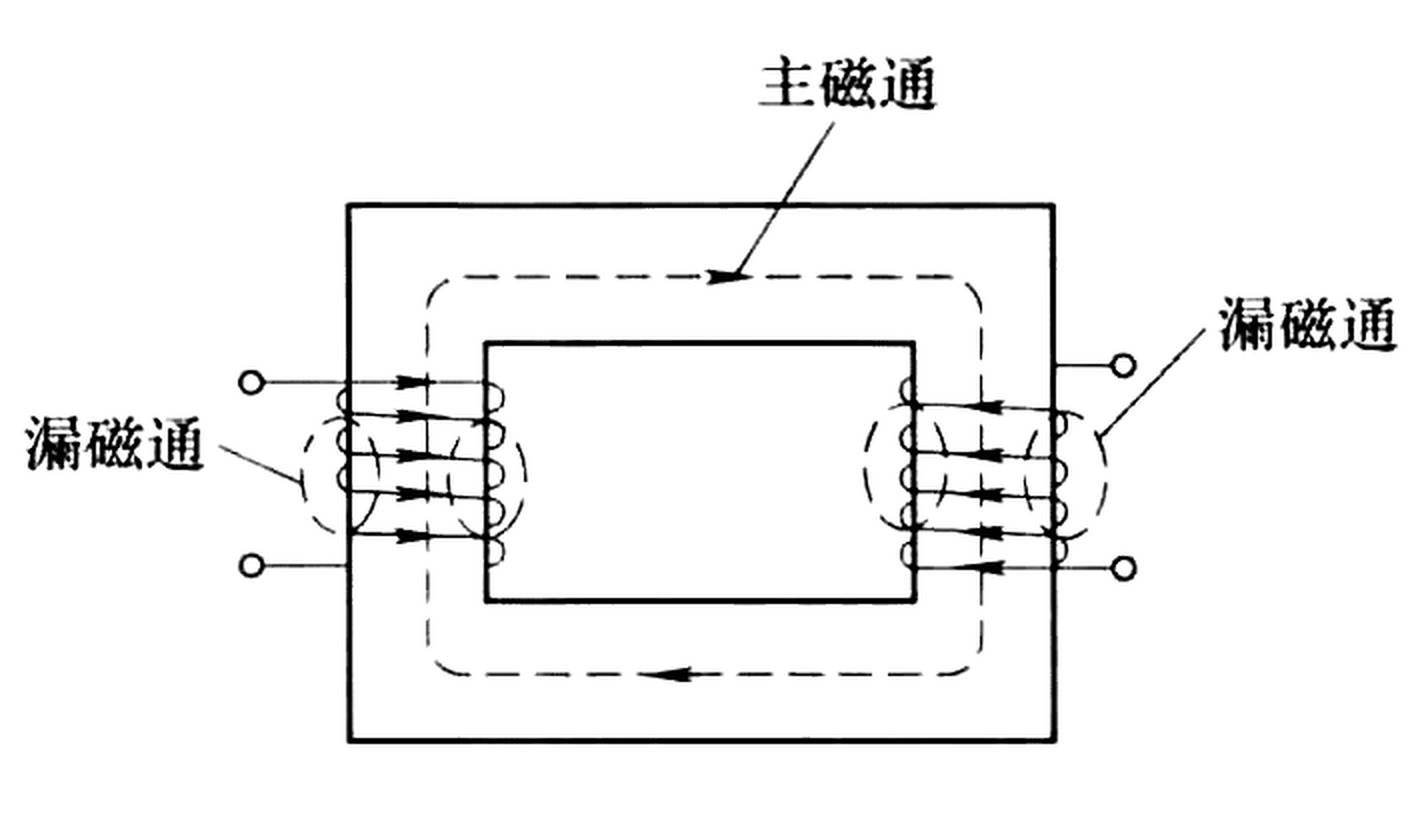
按照磁通所通过的路径不同，磁路可以分为主磁路和漏磁路。以下图中的变压器为例：

• 线圈套装在铁心上，当线圈内通有电流时，载流线圈所产生的绝大部分磁通将在铁心内通过，这部分磁通称为主磁通。主磁通所通过的路径构成主磁路。

• 围绕着载流线圈和部分铁心周围的空间，还存在少量分散磁通，这部分磁通称为漏磁通。漏磁通所通过的路径构成漏磁路。

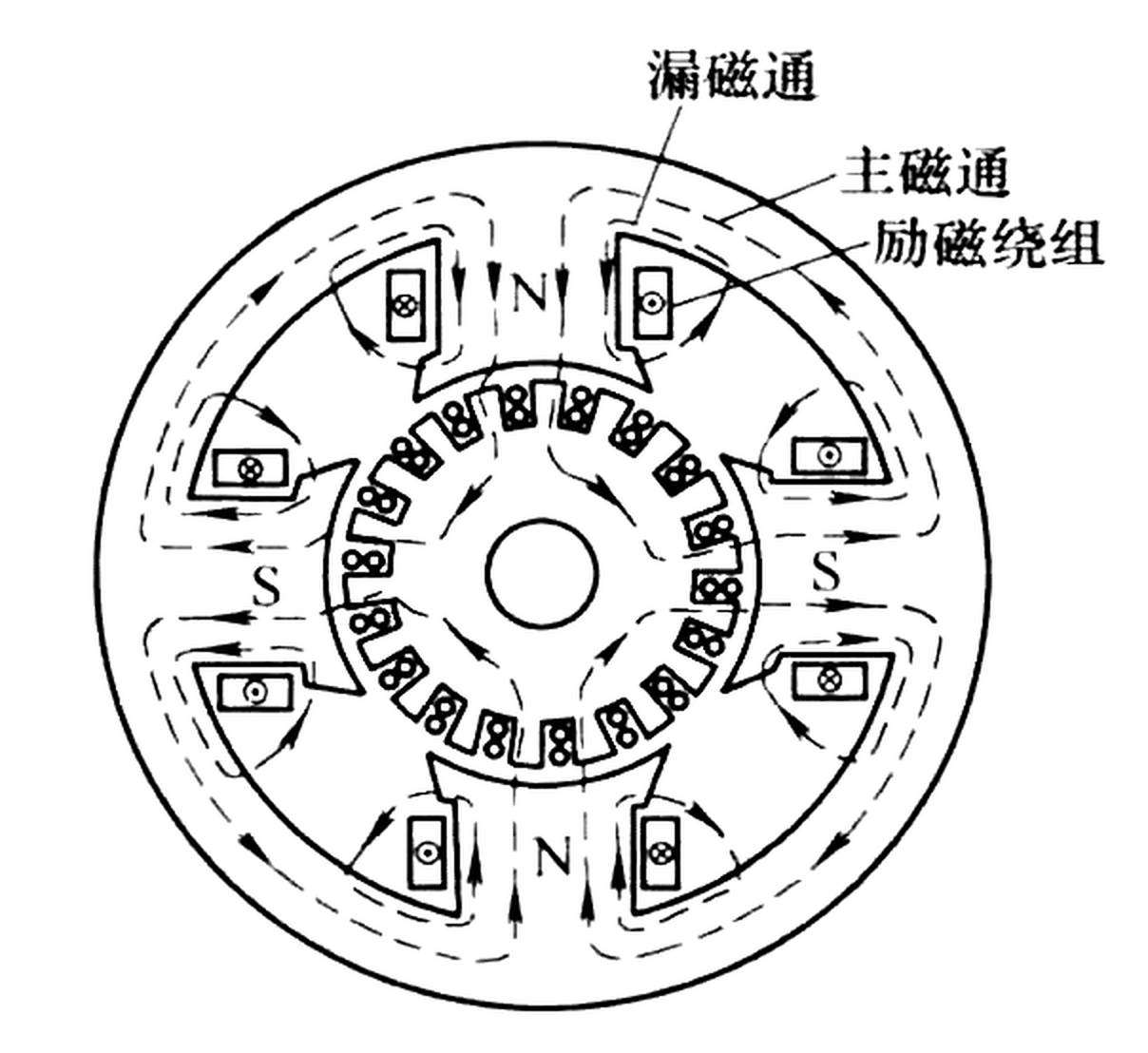
按照产生磁通的励磁电流的不同，磁路可以分为直流磁路和交流磁路。以下图中的四极直流电机为例，其中，产生磁通的载流线圈称为励磁线圈（或励磁绕组），励磁线圈中的电流称为励磁电流：

• 若励磁电流为直流，磁路中的磁通为恒定，不随时间而变化，这种磁路称为直流磁路，例如直流电机的磁路。

• 若励磁电流为交流（常称为激磁电流），磁路中的磁通随时间交变变化，这种磁路称为交流磁路，例如交流铁心线圈、变压器、感应电机的磁路。
  

总结如下：

2. 磁路的基本定律

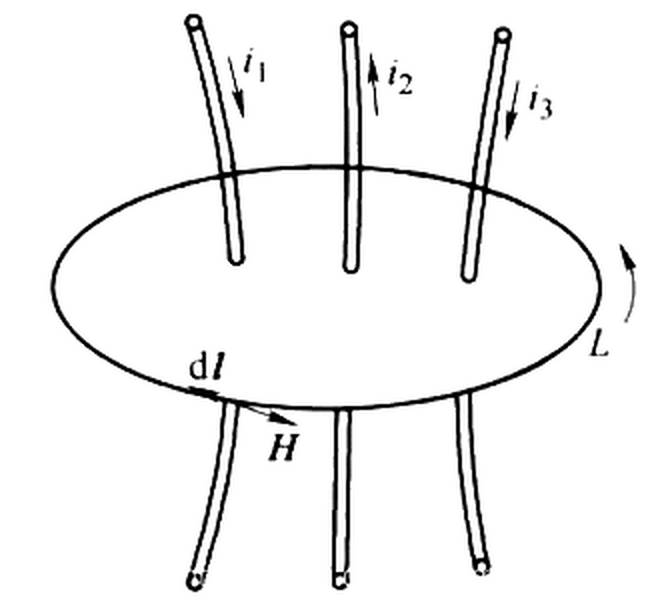
2.1 安培环路定律

沿着任何一条闭合回线 $L$，磁场强度 $H$ 的线积分值
$${\oint }_{L}H\cdot dl$$
恰好等于该闭合回线所包围的总电流值 $\sum i$（代数和），这就是安培环路定律。
$${\oint }_{L}H\cdot dl=\sum i$$
式中，若电流的正方向与闭合回线 $L$ 的环形方向符合右手螺旋关系，则 $i$ 取正号，否则取负号。

2.2 磁路的欧姆定律

下图是一个无分支的铁心磁路，铁心上绕有 $N$ 匝的线圈，线圈中通有电流 $i$，铁心截面积为 $A$，磁路的平均长度为 $l$，铁心的磁导率为 $\mu$。

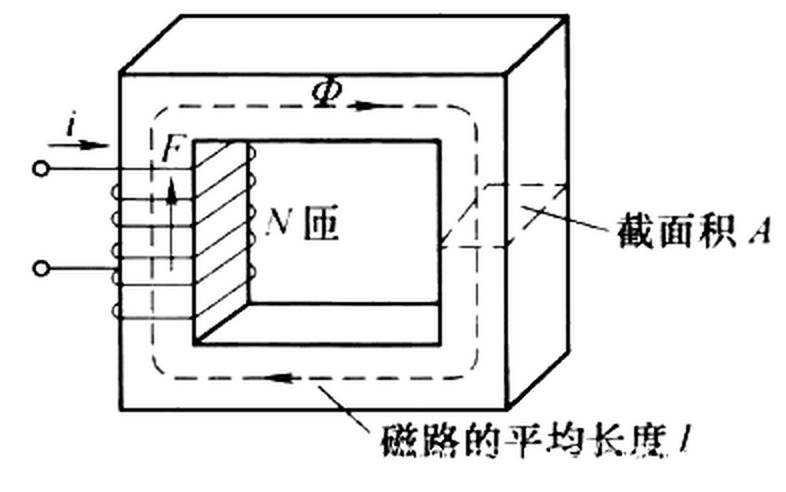
若不计漏磁通，即认为所有磁通都被约束在铁心之内，并认为各截面内的磁场都是均匀分布，$B$（和 $H$）的方向总是沿着回线 $l$ 的切线方向且大小处处相等，此时就有
$${\oint }_{L}H\cdot dl=Hl$$
而闭合回线 $l$ 所包含的总电流 $\sum i=Ni$，这样，2.1中的安培环路定律就可简化为：
$$Ni=Hl$$
由于各截面内的磁通密度 $B$ 为均匀分布，且垂直于各截面，故磁通量 $\Phi$ 将等于磁通密度 $B$ 乘以面积 $A$，即
$$\Phi ={\int }_{A}B\cdot da=BA\text{或}B=\frac{\Phi }{A}$$
再考虑到磁通密度 $B$ 等于磁场强度 $H$ 乘以 $\mu$，即
$$B=\mu H\text{或}H=\frac{B}{\mu }$$
于是 $Ni=Hl$ 可改写为
$$Ni=\frac{B}{\mu }l=\frac{\Phi l}{\mu A}$$
或
$$F=\Phi R_m$$
其中，$F=Ni$，$F$ 为作用在铁心磁路上的安匝数，称为磁路的磁动势，单位为 A。磁动势的方向与线圈电流方向之间符合右手螺旋关系。
$R_m$ 称为磁阻，$R_m=\frac{l}{\mu A}$，单位为 A/Wb。磁阻的倒数称为磁导，用 ${\Lambda }_m$ 表示，${\Lambda }_m=\frac{1}{R_m}$，单位为 Wb/A 或 H（亨）。

$$F=\Phi R_m$$
表示，作用在磁路上的磁动势 $F$ 等于磁路内的磁通量 $\Phi$ 乘以磁阻 $R_m$，此关系与电路中的欧姆定律十分相似，因此也称为磁路的欧姆定律。

这里，我们把磁动势 $F$ 比拟为电路中的电动势 $E$，磁通量 $\Phi$ 比拟为电流 $I$，磁阻 $R_m$ 比拟为电阻 $R$。

无分支铁心磁路的磁路本体及其等效磁路图见下图。

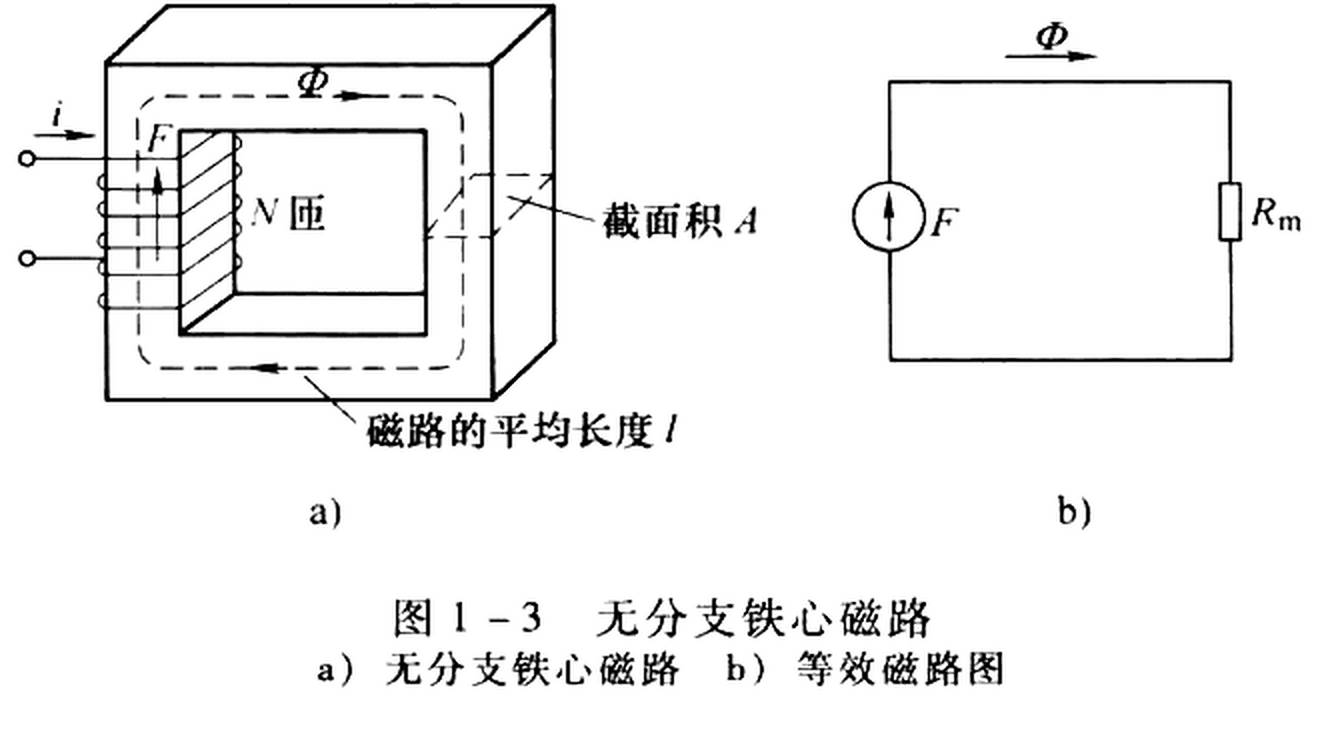
磁阻表达式为 $R_m=\frac{l}{\mu A}$，从中可以看出，$R_m$ 与磁路的平均长度 $l$ 成正比，与磁路的截面积 $A$ 及所用材料的磁导率 $\mu$ 成反比，此式与导体的电阻公式相似。需要注意的是，铁磁材料的磁导率 $\mu$ 不是一个常值，所以由铁磁材料构成的磁路，其磁阻不是常值，而是随着磁路中磁通密度的大小而变化。

因此，磁路中的磁通量 $\Phi$ 不是随着磁动势 $F$ 的增大而正比增大，或者说，$\Phi$ 与 $F$ 之间不是线性关系，这种情况称为磁路是非线性的。

磁路的欧姆定律是由安培环路定律导出的，它对于建立磁路和磁阻的概念很有用。但是，由于铁心磁路是非线性的，所以实际计算时，多数情形下都是利用安培环路定律来计算。

例如：

2.3 磁通连续性定律

2.3.1 定律概述

磁通连续性定律是电磁学的核心定律之一，也是磁路分析的理论基石，其物理本质源于磁场的无源性——磁场线始终以闭合曲线形式存在，不存在起始点与终止点。

2.3.2 数学表达式

$${\oint }_S\mathbf{B}\cdot d\mathbf{S}=0$$
式中各物理量含义如下：

• $\mathbf{B}$：磁感应强度（单位：T），用于定量描述磁场的强弱与方向；
• $d\mathbf{S}$：任意闭合曲面 $S$（在电磁学中又称“高斯面”）上的微小面积元，其方向规定为曲面的外法线方向；
• 积分结果的物理意义：穿过任意闭合曲面的总磁通量恒等于零。

2.3.3 物理意义与磁路关联

从物理现象来看，该定律表明穿过闭合曲面的磁通量（可直观理解为磁场线）“穿入量 = 穿出量”，既不会凭空产生，也不会无故消失。这一核心特性直接为磁路分析中的基尔霍夫第一定律提供了理论依据——在磁路的节点处，流入节点的总磁通与流出节点的总磁通始终满足守恒关系。

2.4 磁路的基尔霍夫第一定律

2.4.1 定律内容

该定律是磁通连续性定律在磁路节点处的具体应用，其逻辑类比于电路分析中的基尔霍夫电流定律（KCL），核心思想是“磁通量守恒”。
在磁路的任意节点（即多段磁路的交汇点），流入节点的总磁通量等于流出节点的总磁通量；为便于定量计算，可规定“流入节点的磁通为正，流出节点的磁通为负”，此时节点处所有磁通量的代数和恒为零。

2.4.2 数学表达式

$$\sum _{k=1}^n{\Phi }_k=0$$
式中各参数含义如下：

• $n$：汇聚于该节点的磁路段数；
• ${\Phi }_k$：第 $k$ 段磁路的磁通量（单位：Wb），其正负号由磁通的实际方向与“流入为正、流出为负”的规定相对应。

2.4.3 物理意义

磁通量在节点处既不会“堆积”也不会“损耗”，这一特性本质上是磁场无源性的延伸，与电路中“节点电流守恒（基于电荷守恒）”的逻辑完全一致。

2.5 磁路的基尔霍夫第二定律

2.5.1 定律内容

该定律是安培环路定律在闭合磁路中的推导结果，其分析逻辑类比于电路中的基尔霍夫电压定律（KVL），核心思想是“磁动势与磁压降的平衡”。
在磁路的任意闭合回路中，所有磁路段的磁压降（简称“磁压”）的代数和，等于该回路中所有励磁绕组的磁动势的代数和。

2.5.2 数学表达式

$$\sum _{k=1}^m{H}_k{l}_k=\sum _{j=1}^p{N}_j{i}_j$$

2.5.3 式中参数说明

为清晰区分各物理量，下表对公式中涉及的参数进行详细说明：

符号	物理量名称	单位	含义与关联
$H_k$	第 $k$ 段磁路的磁场强度	A/m	反映磁场对磁通的“驱动能力”及磁场的空间分布特性，与磁感应强度的关系为 $B=\mu H$（$\mu$ 为磁导率）
$l_k$	第 $k$ 段磁路的平均长度	m	描述磁路几何特征的关键参数，因磁路截面可能存在不均匀性，故取平均长度以简化计算
$H_k{l}_k$	第 $k$ 段磁路的磁压降（简称“磁压”）	A	类比于电路中的“电压降 $IR$”，用于定量描述磁路对磁通的阻碍作用
$N_j$	第 $j$ 个励磁绕组的匝数	匝	励磁绕组的结构参数，反映绕组的匝数特性
$i_j$	第 $j$ 个励磁绕组的励磁电流	A	驱动磁通产生的电流，是磁路中磁通的“激励源”
$N_j{i}_j$	第 $j$ 个励磁绕组的磁动势（简称“磁势”）	A	类比于电路中的“电动势 $E$”，是驱动磁路中产生磁通的核心“动力”
$m$	闭合回路中磁路段数	-	表示闭合磁路中被拆分的磁路段数，用于计算磁压降的总和
$p$	闭合回路中励磁绕组数	-	表示闭合磁路中包含的励磁绕组数量，用于计算磁动势的总和

• $m$（闭合回路中磁路段数）：

  • 单位：无单位（无量纲）
  • 含义：表示闭合磁路中被拆分的磁路段数。这是一个计数参数，用于描述磁路的几何结构，帮助计算磁压降的总和。
  • 关联：在公式 ${\sum }_{k=1}^m{H}_k{l}_k$ 中，$m$ 表示磁路段的总数，每一段磁路都有一个磁场强度 $H_k$ 和长度 $l_k$，通过这些参数计算磁压降的总和。

• $p$（闭合回路中励磁绕组数）：

  • 单位：无单位（无量纲）
  • 含义：表示闭合磁路中包含的励磁绕组数量。这也是一个计数参数，用于描述磁路中的励磁绕组结构，帮助计算磁动势的总和。
  • 关联：在公式 ${\sum }_{j=1}^p{N}_j{i}_j$ 中，$p$ 表示励磁绕组的总数，每个绕组都有一个匝数 $N_j$ 和电流 $i_j$，通过这些参数计算磁动势的总和。

2.5.4 符号规则与推导逻辑

2.5.4.1 符号规定

为确保计算结果的准确性，需明确以下符号规则：

• 对于磁压降 $H_k{l}_k$：若某段磁路的磁场强度 $H_k$ 方向与闭合回路的“绕行方向”（可任意规定）一致，则该段的 $H_k{l}_k$ 取正；反之则取负。
• 对于磁动势 $N_j{i}_j$：若励磁电流 $i_j$ 产生的磁动势方向与闭合回路的绕行方向符合“右手螺旋关系”（右手四指沿绕行方向，大拇指指向即为磁动势正方向），则该绕组的 $N_j{i}_j$ 取正；反之则取负。

2.5.4.2 推导依据

该定律的数学表达式源于安培环路定律。对闭合磁路应用安培环路定律 ${\oint }_L\mathbf{H}\cdot d\mathbf{l}=\sum i$，可将闭合回路拆分为 $m$ 段“均匀磁路”（每段磁路的磁场强度 $H_k$ 大小恒定、方向沿磁路长度方向），此时安培环路定律的线积分可拆分为各段磁路 $H_k{l}_k$ 的代数和；而公式右侧的“总电流 $\sum i$”等于各励磁绕组的“匝数×电流”（即安匝数）之和 $\sum N_j{i}_j$，最终推导得到磁路的基尔霍夫第二定律的数学表达式。

2.5.5 磁路 - 电路类比

为帮助理解，可将该定律与电路中的 KVL（$\sum IR=\sum E$）进行类比，二者的对应关系如下：

• 磁路中的磁动势 $N_i$ ↔ 电路中的电动势 $E$（均为“驱动量”，分别驱动磁通、电流产生）；
• 磁路中的磁压降 $Hl$ ↔ 电路中的电压降 $IR$（均为“阻碍量”，分别阻碍磁通、电流的流通）；
• 二者的核心逻辑一致：均反映“闭合回路中驱动量与阻碍量的平衡关系”。
  进一步地，磁路中引入“磁阻”概念（$R_m=\frac{l}{\mu S}$，其中 $S$ 为磁路截面积），其类比于电路中的电阻 $R$；磁路中的磁通 $\Phi$ 类比于电路中的电流 $I$。因此，磁压降还可表示为“磁通×磁阻”，即 $\Phi \times R_m$，与电路中“电压降 = 电流×电阻”（$IR$）的形式完全对应。

---

磁路的基本定理

新歌_ 已于 2023-07-20 20:27:00 修改

基本物理量

• 磁通量（Magnetic Flux）：符号 $\Phi$，单位韦伯（Weber，符号 Wb）。
• 磁场强度（Magnetic Field Strength）：符号 $H$，单位安培/米（A/m）。
• 磁感应强度（Magnetic Flux Density）：符号 $B$，单位特斯拉（Tesla，符号 T）。
• 磁导率（Magnetic Permeability）：符号 $\mu$，单位亨利/米（H/m）。
• 磁导（Wb/A 或 H）
• 截面积 $A$（$m^2$）
• 匝数 $N$
• 电感 $L$，单位 H（亨）
• 磁链 $\psi =N\Phi$，单位：韦伯（Wb）

磁路欧姆定律

磁路欧姆定律（Ohm’s law for magnetic circuits）是指磁路中磁动势（magnetomotive force，MMF）与磁通量（magnetic flux，$\Phi$）之间的关系。它与电路欧姆定律类似，可以表示为：
$$F=\Sigma Ni=\Sigma Hl=\Phi R=\frac{\Phi }{\Lambda }$$
其中，$F$ 是磁动势，单位是安培圈（ampere-turns，符号 AT），$\Phi$ 是磁通量，单位是韦伯（weber，符号 Wb），$R$ 是磁阻（reluctance），单位是 1/亨利（per henry）。

磁动势 $F$ 可以理解为驱动磁通量流过磁路的力量，它与电动势（electromotive force，EMF）类似。磁阻 $R$ 可以理解为阻碍磁通量流过磁路的阻力，它与电阻（resistance）类似。

常用公式

这些物理量之间也存在着一些基本的关系。例如：

• $\Phi =BA$
• $B=H\mu$
• $R=\frac{l}{A\mu }=\frac{1}{\Lambda }$
• $\psi =N\Phi =\frac{NF}{R_m}=\frac{N(Ni)}{R_m}=Li$
• $L=\Lambda N^2=\frac{N^2}{R_m}$
• $X_{\text{电抗}}=\omega L=2\pi f{N}^2\Lambda =2\pi f{N}^2\frac{1}{R_m}=2\pi f{N}^2\frac{A\mu }{l}$

相关的基本定理和法则

左手定则 & 右手定则

左手定则和右手定则是两个用于判断电磁现象中电流、磁场和力的方向关系的定则。

左手定则

通常用于判断电动机中电流、磁场和力的方向关系。具体方法是：将左手伸开，让拇指、食指和中指垂直相交，且食指指向磁场方向，中指指向电流方向，那么拇指所指的方向就是电动机中电磁力的方向。

右手定则

通常用于判断发电机中电流、磁场和力的方向关系。具体方法是：
将右手握拳，让拇指指向磁场方向，其余四指弯曲指向导体运动的方向，那么拇指所指的方向就是发电机中感应电流的方向。

电磁感应定律

电磁感应定律是指：当磁通量的变化率在一定的闭合回路上产生时，该回路中就会产生感应电动势，其大小与磁通量变化率成正比。可以用以下公式表示：
$$\epsilon =-\frac{d\psi }{dt}=-N\frac{d{\Phi }_B}{dt}$$
其中，$\epsilon$ 是感应电动势，单位是伏特（volt，符号 V），${\Phi }_B$ 是磁通量，单位是韦伯（weber，符号 Wb），$t$ 是时间，单位是秒（second，符号 s）。

上式中的负号表示感应电动势的方向与磁通量变化的方向相反。这一点可以通过楞次定律（Lenz’s law）来解释：感应电流的方向总是阻碍引起它的磁通量变化。

楞次定律

楞次定律（Lenz’s law）是指感应电流的方向总是阻碍引起它的磁通量变化。它是法拉第电磁感应定律的一个重要补充，用于确定感应电流的方向。

楞次定律可以用来解释许多电磁现象。例如，在一个闭合导体回路中，如果磁通量发生变化，那么回路中就会产生感应电流。根据楞次定律，这个感应电流的方向总是阻碍磁通量的变化。也就是说，如果磁通量增加，那么感应电流就会产生一个与原磁场相反的磁场；如果磁通量减小，那么感应电流就会产生一个与原磁场相同的磁场。

常用铁磁材料及其特性

磁化曲线

我们可以看到，起始阶段磁导率低，ab段磁导率高，到达膝点之后，磁场饱和，磁导率又重新开始下降。
因此我们设计电机和变压器时，为了主磁路获得较大的磁通量而又不过分增大励磁电流，常把铁芯的工作磁通密度选择在膝点附近。

磁滞回线

铁磁材料

硬磁（永磁）材料

磁滞回线宽，剩磁 $B_r$ 和矫顽力 $H_c$ 都很大的材料。

软磁材料

磁滞回线窄，剩磁 $B_r$ 和矫顽力 $H_c$ 都很小的材料。
常用的材料有铸铁、铸钢、硅钢片。
软磁材料磁导率高，常用于制造电机和变压器铁芯。

铁芯损耗

铁芯损耗 = 磁滞损耗 + 涡流损耗

磁滞损耗

磁滞损耗公式：
$$P_h=C_{h}f{B}_m^{n}V$$
其中，$C_h$ 是铁芯的磁滞损耗系数，$f$ 是工作频率，$B_m$ 是铁芯中最大的峰值磁感应强度，对一般电工钢片，$n=1.6\sim 2.3$，建议取 2，$V$ 是铁芯的体积。

涡流损耗

涡流损耗公式：
$$P_e=C_e{f}^2{B}_m^2{\Delta }^{2}V$$
其中，$C_e$ 是涡流损耗系数，大小取决于电阻率，$f$ 是工作频率，$B_m$ 是铁芯中最大的峰值磁感应强度，$\Delta$ 是涡流路径的平均厚度，$V$ 是铁芯的体积。
电机和变压器常用硅钢片厚度（0.35 mm \sim 0.5 mm）

以上公式仅为常见的简化形式，实际应用中需要结合具体的情况来确定参数的取值。

铁芯损耗

$$P_{Fe}=P_h+P_e=C_{h}f{B}_m^{n}V+C_e{f}^2{B}_m^2{\Delta }^{2}V$$
一般的电工钢片，可近似地写成
$$P_{Fe}=C_{Fe}{f}^{1.3}{B}_m^{2}G$$
$C_{Fe}$ 为铁芯损耗系数；$G$ 为铁芯重量

由上式知，铁芯损耗与频率 1.3 次方，磁通密度的平方，铁芯重量三者成正比。

常识

• 黄绿红，对应 ABC 三相
• 蓝色，对应零线
• 黄绿相间，对应地线

---

via：

• 磁路的基本概念与定律解析 - 优快云 博客
  https://blog.youkuaiyun.com/mahoon411/article/details/119053540
• 磁路的基本定理_磁路定理 - 优快云 博客
  https://blog.youkuaiyun.com/weixin_53683736/article/details/131623098