注:本文为 “张量分解” 相关合辑。
图片清晰度受引文原图所限。
略作重排,如有内容异常,请看原文。
张量分解
张量介绍
张量(tensor)是一种多维数据存储形式,数据的维度被称为张量的阶。它可以视为向量和矩阵在多维空间中的推广,向量可看作一维张量,矩阵可看作二维张量。以下是一个三阶张量的例子,它有三个维度,即 3 个 mode:
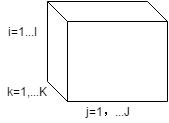
需要注意的是,此处所说的张量是具有某种排列形式的数据集合,与物理中的张量场不同。
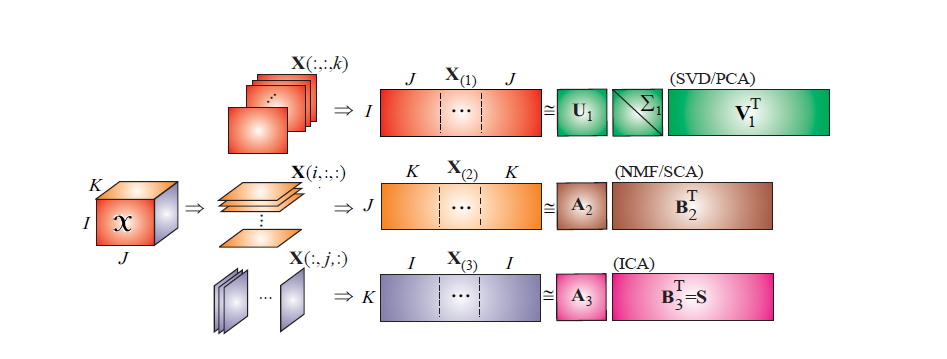
传统的处理高维数据的方法(如 ICA、PCA、SVD 和 NMF)通常将数据展成二维的矩阵形式进行处理,这种方式会使数据的结构信息丢失(例如图像的邻域信息丢失),导致求解过程往往变得病态。而采用张量对数据进行存储,能够保留数据的结构信息,因此在图像处理以及计算机视觉等领域得到了广泛应用。张量分解中常见的两种分解是 CP 分解(Canonical Polyadic Decomposition,CPD)和 Tucker 分解(Tucker Decomposition)。下面将重点介绍这两种分解,并阐述它们在图像处理中的一些应用。
张量定义及运算
张量(Tensor)
一个 N N N 阶 I 1 × I 2 × ⋯ × I N I_{1} \times I_{2} \times \dots \times I_{N} I1×I2×⋯×IN 维的张量可以表示为 Y ∈ R I 1 × I 2 × ⋯ × I N Y \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}} Y∈RI1×I2×⋯×IN。张量中的每一个元素可以由 y i 1 i 2 … i n y_{i_{1} i_{2} \dots i_{n}} yi1i2…in 表示,其中 i n ∈ { 1 , 2 , … , I n } i_{n} \in \{1,2,\dots,I_{n}\} in∈{1,2,…,In}。
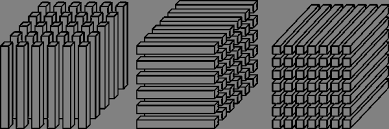
纤维(Fiber)
纤维是指从张量中抽取向量的操作。类似于矩阵操作,固定其他维度,只保留一个维度变化,可以得到纤维的概念。例如,对上图中的三阶张量分别按照 I、J、K 三个 mode 进行 Fiber 操作,可以得到如图所示的 x : j k x_{:jk} x:jk、 x i : k x_{i:k} xi:k、 x i j : x_{ij:} xij: 三个维度的纤维:
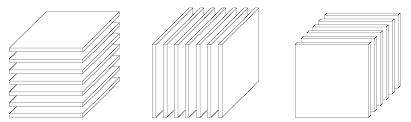
切片(Slice)
切片操作是指在张量中抽取矩阵的操作。在张量中,若保留两个维度变化,其他维度固定,可以得到一个矩阵,该矩阵即为张量的切片。对图中的张量分别按照 I、J、K 三个方向进行操作,可以得到如图所示的 x i : : x_{i::} xi::、 x : j : x_{:j:} x:j:、 x : : k x_{::k} x::k 三个维度的切片:
内积(Inner product)
两个大小相同的张量
X
,
Y
∈
R
I
1
×
I
2
×
⋯
×
I
N
X,Y \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X,Y∈RI1×I2×⋯×IN 的内积定义为张量中相对应的元素的乘积之和,即:
⟨
X
,
Y
⟩
=
∑
i
1
=
1
I
1
∑
i
2
=
1
I
2
⋯
∑
i
N
=
1
I
N
x
i
1
i
2
…
i
N
y
i
1
i
2
…
i
N
\langle X,Y \rangle = \sum_{i_{1}=1}^{I_{1}} \sum_{i_{2}=1}^{I_{2}} \dots \sum_{i_{N}=1}^{I_{N}} x_{i_{1} i_{2} \dots i_{N}} y_{i_{1} i_{2} \dots i_{N}}
⟨X,Y⟩=i1=1∑I1i2=1∑I2⋯iN=1∑INxi1i2…iNyi1i2…iN
相应地,张量
X
∈
R
I
1
×
I
2
×
⋯
×
I
N
X \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X∈RI1×I2×⋯×IN 的范数定义为:
∥
X
∥
=
∑
i
1
=
1
I
1
∑
i
2
=
1
I
2
⋯
∑
i
N
=
1
I
N
x
i
1
i
2
…
i
N
2
\|X\| = \sqrt{\sum_{i_{1}=1}^{I_{1}} \sum_{i_{2}=1}^{I_{2}} \dots \sum_{i_{N}=1}^{I_{N}} x_{i_{1} i_{2} \dots i_{N}}^{2}}
∥X∥=i1=1∑I1i2=1∑I2⋯iN=1∑INxi1i2…iN2
即所有元素的平方和的平方根。
矩阵展开(Unfolding-Matricization)
张量的矩阵展开是将一个张量的元素重新排列(即对张量的 mode-n 的纤维进行重新排列),得到一个矩阵的过程。张量 X ∈ R I 1 × I 2 × ⋯ × I N X \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}} X∈RI1×I2×⋯×IN 在第 n n n 维度上展开矩阵表示为 X ( n ) ∈ R I n × ( I 1 × I 2 × … I n − 1 I n + 1 ⋯ × I N ) X_{(n)} \in \mathbb{R}^{I_{n} \times (I_{1} \times I_{2} \times \dots I_{n-1} I_{n+1} \dots \times I_{N})} X(n)∈RIn×(I1×I2×…In−1In+1⋯×IN)。对一个三阶张量按照 I、J、K 三个方向进行矩阵展开得到的矩阵如下图:

外积(Outer Product)
定义张量
X
∈
R
I
1
×
I
2
×
⋯
×
I
N
X \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X∈RI1×I2×⋯×IN 和张量
Y
∈
R
J
1
×
J
2
×
⋯
×
J
M
Y \in \mathbb{R}^{J_{1} \times J_{2} \times \dots \times J_{M}}
Y∈RJ1×J2×⋯×JM 的外积为:
Z
=
X
∘
Y
∈
R
I
1
×
I
2
×
⋯
×
I
N
×
J
1
×
J
2
×
⋯
×
J
M
Z = X \circ Y \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N} \times J_{1} \times J_{2} \times \dots \times J_{M}}
Z=X∘Y∈RI1×I2×⋯×IN×J1×J2×⋯×JM
其中:
z
i
1
,
i
2
,
…
,
i
N
,
j
1
,
j
2
,
…
,
j
M
=
x
i
1
,
i
2
,
…
,
i
N
×
y
j
1
,
j
2
,
…
,
j
M
z_{i_{1},i_{2},\dots,i_{N},j_{1},j_{2},\dots,j_{M}} = x_{i_{1},i_{2},\dots,i_{N}} \times y_{j_{1},j_{2},\dots,j_{M}}
zi1,i2,…,iN,j1,j2,…,jM=xi1,i2,…,iN×yj1,j2,…,jM
即张量
Z
Z
Z 是张量
X
X
X 和张量
Y
Y
Y 中的每一个元素的乘积构成的。特别地,如果
X
X
X 和
Y
Y
Y 分别是一个向量,那么它们的外积是一个秩为 1 的矩阵;如果
X
X
X、
Y
Y
Y 和
Z
Z
Z 分别是一个向量,那么它们的外积是一个秩为 1 的三阶张量。
Kronecker 乘积(Kronecker Product)
Kronecker 乘积定义在两个矩阵 A ∈ R I × J \mathbf{A} \in \mathbb{R}^{I \times J} A∈RI×J、 B ∈ R K × L \mathbf{B} \in \mathbb{R}^{K \times L} B∈RK×L 上的运算:
A ⊗ B = [ a 11 B a 12 B ⋯ a 1 J B a 21 B a 22 B ⋯ a 2 J B ⋮ ⋮ ⋱ ⋮ a I 1 B a I 2 B ⋯ a I J B ] ∈ R I K × J L \mathbf{A} \otimes \mathbf{B} = \begin{bmatrix} a_{11}\mathbf{B} & a_{12}\mathbf{B} & \cdots & a_{1J}\mathbf{B} \\ a_{21}\mathbf{B} & a_{22}\mathbf{B} & \cdots & a_{2J}\mathbf{B} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}\mathbf{B} & a_{I2}\mathbf{B} & \cdots & a_{IJ}\mathbf{B} \end{bmatrix} \in \mathbb{R}^{IK \times JL} A⊗B= a11Ba21B⋮aI1Ba12Ba22B⋮aI2B⋯⋯⋱⋯a1JBa2JB⋮aIJB ∈RIK×JL
Hadamard 乘积(Hadamard Product)
Hadamard 乘积定义在两个相同大小的矩阵 A ∈ R I × J \mathbf{A} \in \mathbb{R}^{I \times J} A∈RI×J、 B ∈ R I × J \mathbf{B} \in \mathbb{R}^{I \times J} B∈RI×J 上的运算:
A ∗ B = [ a 11 b 11 a 12 b 12 ⋯ a 1 J b 1 J a 21 b 21 a 22 b 22 ⋯ a 2 J b 2 J ⋮ ⋮ ⋱ ⋮ a I 1 b I 1 a I 2 b I 2 ⋯ a I J b I J ] ∈ R I × J \mathbf{A} * \mathbf{B} = \begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} & \cdots & a_{1J}b_{1J} \\ a_{21}b_{21} & a_{22}b_{22} & \cdots & a_{2J}b_{2J} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}b_{I1} & a_{I2}b_{I2} & \cdots & a_{IJ}b_{IJ} \end{bmatrix} \in \mathbb{R}^{I \times J} A∗B= a11b11a21b21⋮aI1bI1a12b12a22b22⋮aI2bI2⋯⋯⋱⋯a1Jb1Ja2Jb2J⋮aIJbIJ ∈RI×J
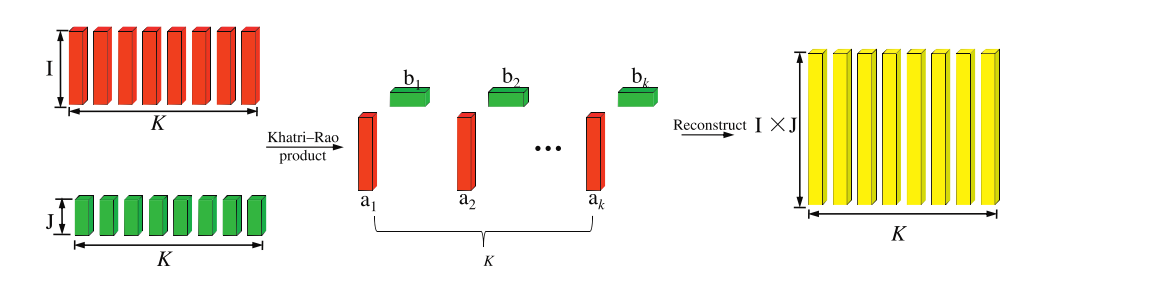
Khatri-Rao 乘积(Khatri-Rao Product)
Khatri-Rao 乘积定义了两个相同列数的矩阵
A
∈
R
I
×
K
\mathbf{A} \in \mathbb{R}^{I \times K}
A∈RI×K、
B
∈
R
J
×
K
\mathbf{B} \in \mathbb{R}^{J \times K}
B∈RJ×K 上的操作,其过程如下图所示:
A
⊙
B
=
[
a
1
⊗
b
1
a
2
⊗
b
2
…
a
K
⊗
b
K
]
∈
R
I
J
×
K
\mathbf{A} \odot \mathbf{B} = \left[ \begin{array}{cccc} \mathbf{a}_{1} \otimes \mathbf{b}_{1} & \mathbf{a}_{2} \otimes \mathbf{b}_{2} & \dots & \mathbf{a}_{K} \otimes \mathbf{b}_{K} \end{array} \right] \in \mathbb{R}^{IJ \times K}
A⊙B=[a1⊗b1a2⊗b2…aK⊗bK]∈RIJ×K
张量与矩阵的模积(Mode-n Product)
张量与矩阵的模积定义了一个张量
X
∈
R
I
1
×
I
2
×
⋯
×
I
N
X \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X∈RI1×I2×⋯×IN 和一个矩阵
U
∈
R
J
×
I
n
\mathbf{U} \in \mathbb{R}^{J \times I_{n}}
U∈RJ×In 的 n-mode 乘积
(
X
×
n
U
)
∈
R
I
1
×
⋯
×
I
n
−
1
×
J
×
I
n
+
1
×
⋯
×
I
N
(X \times_{n} \mathbf{U}) \in \mathbb{R}^{I_{1} \times \dots \times I_{n-1} \times J \times I_{n+1} \times \dots \times I_{N}}
(X×nU)∈RI1×⋯×In−1×J×In+1×⋯×IN,其元素定义为:
(
X
×
n
U
)
i
1
…
i
n
−
1
j
i
n
+
1
…
i
N
=
∑
i
n
=
1
I
n
x
i
1
i
2
…
i
N
u
j
i
n
(X \times_{n} \mathbf{U})_{i_{1} \dots i_{n-1} j i_{n+1} \dots i_{N}} = \sum_{i_{n}=1}^{I_{n}} x_{i_{1} i_{2} \dots i_{N}} u_{j i_{n}}
(X×nU)i1…in−1jin+1…iN=in=1∑Inxi1i2…iNujin
该定义可以写成沿 mode-n 展开的形式为:
Y
=
X
×
n
U
⇔
Y
(
n
)
=
U
X
(
n
)
Y = X \times_{n} \mathbf{U} \Leftrightarrow \mathbf{Y}_{(n)} = \mathbf{U} \mathbf{X}_{(n)}
Y=X×nU⇔Y(n)=UX(n)
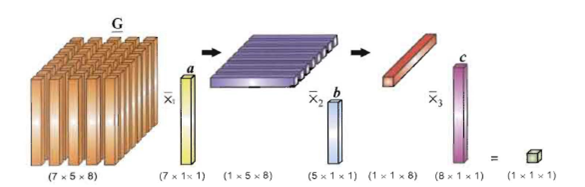
如果
J
<
I
n
J < I_{n}
J<In,那么张量和矩阵的乘积可以看作是一个降维的过程,它把一个高维度的张量映射到一个低维度的张量空间。图 \ref{fig:tensorMatrixProduct} 演示了一个张量
G
∈
R
7
×
5
×
8
G \in \mathbb{R}^{7 \times 5 \times 8}
G∈R7×5×8 和一个矩阵
A
∈
R
4
×
7
A \in \mathbb{R}^{4 \times 7}
A∈R4×7 的乘积最终得到张量
Y
∈
R
4
×
5
×
8
Y \in \mathbb{R}^{4 \times 5 \times 8}
Y∈R4×5×8,张量的第一个维度由 7 变成了 4。

张量与向量的模积(Mode-n Product)
张量与向量的模积定义了一个张量
X
∈
R
I
1
×
I
2
×
⋯
×
I
N
X \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X∈RI1×I2×⋯×IN 与向量
v
∈
R
I
n
\mathbf{v} \in \mathbb{R}^{I_{n}}
v∈RIn 的运算为:
(
X
×
n
v
)
i
1
…
i
n
−
1
i
n
+
1
…
i
N
=
∑
i
n
=
1
I
n
x
i
1
i
2
…
i
N
v
i
n
(X \times_{n} \mathbf{v})_{i_{1} \dots i_{n-1} i_{n+1} \dots i_{N}} = \sum_{i_{n}=1}^{I_{n}} x_{i_{1} i_{2} \dots i_{N}} v_{i_{n}}
(X×nv)i1…in−1in+1…iN=in=1∑Inxi1i2…iNvin
一个向量和一个张量进行模乘可以减少张量的阶数,下图演示了一个张量的阶数由 3 阶变为 0 阶的过程。
张量分解 - CP 分解
CP 分解(Canonical Polyadic Decomposition)
1927 年,Hitchcock 提出了 CP 分解。CP 分解将一个
N
N
N 阶张量
X
∈
R
I
1
×
I
2
×
⋯
×
I
N
\mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X∈RI1×I2×⋯×IN 分解为
R
R
R 个秩为 1 的张量和的形式,即:
X
=
∑
r
=
1
R
λ
r
a
r
(
1
)
∘
a
r
(
2
)
∘
⋯
∘
a
r
(
N
)
\mathcal{X} = \sum_{r=1}^{R} \lambda_{r} a_{r}^{(1)} \circ a_{r}^{(2)} \circ \dots \circ a_{r}^{(N)}
X=r=1∑Rλrar(1)∘ar(2)∘⋯∘ar(N)
通常情况下,
a
r
(
n
)
a_{r}^{(n)}
ar(n) 是一个单位向量。定义
A
(
n
)
=
[
a
1
n
a
2
n
…
a
R
n
]
A^{(n)} = [a_{1}^{n} \ a_{2}^{n} \ \dots \ a_{R}^{n}]
A(n)=[a1n a2n … aRn],
D
=
diag
(
λ
)
D = \text{diag}(\lambda)
D=diag(λ),那么上述公式可以写为:
X
=
D
×
1
A
(
1
)
×
2
A
(
2
)
⋯
×
N
A
(
N
)
\mathcal{X} = D \times_{1} A^{(1)} \times_{2} A^{(2)} \cdots \times_{N} A^{(N)}
X=D×1A(1)×2A(2)⋯×NA(N)
矩阵的表达形式为:
X
(
n
)
=
A
n
D
(
A
(
N
)
⨀
⋯
⨀
A
(
n
+
1
)
⨀
A
(
n
−
1
)
⋯
⨀
A
1
)
T
X_{(n)} = A^{n} D (A^{(N)} \bigodot \dots \bigodot A^{(n+1)} \bigodot A^{(n-1)} \dots \bigodot A^{1})^{T}
X(n)=AnD(A(N)⨀⋯⨀A(n+1)⨀A(n−1)⋯⨀A1)T
当张量
X
\mathcal{X}
X 的阶数为 3 时,其分解的形式如下图所示:

张量的低秩近似
在矩阵中,定义最小的秩为 1 的矩阵和的个数为矩阵的秩。类似地,
R
R
R 的最小值为张量的秩,记作
Rank
(
X
)
=
R
\text{Rank}(\mathcal{X}) = R
Rank(X)=R,这样的 CP 分解也称为张量的秩分解。需要注意的是,在张量中,秩的定义是不唯一的,张量秩的个数求解是一个 NP 问题。对于一个矩阵
A
A
A,其 SVD 分解定义为:
A
=
∑
r
=
1
R
σ
r
u
r
∘
v
r
,
σ
1
≥
σ
2
≥
⋯
≥
σ
R
≥
0
A = \sum_{r=1}^{R} \sigma_{r} u_{r} \circ v_{r}, \quad \sigma_{1} \geq \sigma_{2} \geq \dots \geq \sigma_{R} \geq 0
A=r=1∑Rσrur∘vr,σ1≥σ2≥⋯≥σR≥0
取 SVD 分解得到的前
k
k
k 个因子作为矩阵
A
A
A 的近似,可以得到矩阵
A
A
A 的低秩近似。类似地,取张量的前
k
k
k 个因子作为张量
X
\mathcal{X}
X 的低秩近似,即:
X
=
∑
k
=
1
K
λ
k
a
k
(
1
)
∘
a
k
(
2
)
∘
⋯
∘
a
k
(
N
)
\mathcal{X} = \sum_{k=1}^{K} \lambda_{k} a_{k}^{(1)} \circ a_{k}^{(2)} \circ \dots \circ a_{k}^{(N)}
X=k=1∑Kλkak(1)∘ak(2)∘⋯∘ak(N)
与矩阵的低秩近似不同,张量的最佳 Rank-n 近似并不包括在其最佳 Rank-(n+1) 近似中,即张量的秩 Rank-n 近似无法渐进地得到。
CP 的求解
CP 分解的求解首先要确定分解的秩 1 张量的个数。由于张量的秩 Rank-n 近似无法渐进地得到,通常通过迭代的方法对 R R R 从 1 开始遍历,直到找到一个合适的解。当数据无噪声时,重构误差为 0 所对应的解即为 CP 分解的解;当数据有噪声时,可以通过 CORCONDIA 算法估计 R R R。当分解的秩 1 张量的个数确定下来之后,可以通过交替最小二乘方法对 CP 分解进行求解。以下以三阶张量为例对 ALS 算法进行阐述。
假设
X
∈
R
I
×
J
×
K
\mathcal{X} \in \mathbb{R}^{I \times J \times K}
X∈RI×J×K 是一个三阶张量,对它进行张量分解的目标表达式为:
min
X
^
∥
X
−
X
^
∥
,
X
^
=
∑
r
=
1
R
λ
r
a
r
∘
b
r
∘
c
r
=
[
[
λ
;
A
,
B
,
C
]
]
\min_{\hat{\mathcal{X}}} \| \mathcal{X} - \hat{\mathcal{X}} \|, \quad \hat{\mathcal{X}} = \sum_{r=1}^{R} \lambda_{r} a_{r} \circ b_{r} \circ c_{r} = \left[\kern-0.15em\left[ \lambda ; A,B,C \right]\kern-0.15em\right]
X^min∥X−X^∥,X^=r=1∑Rλrar∘br∘cr=[[λ;A,B,C]]
ALS 算法首先固定
B
B
B、
C
C
C 去求解
A
A
A,接着固定
A
A
A 和
C
C
C 去求解
B
B
B,然后固定
B
B
B 和
C
C
C 去求解
A
A
A,如此不断重复迭代直到达到收敛条件。固定矩阵
B
B
B 和
C
C
C,可以得到上述式子在 mode-1 矩阵展开时的形式为:
min
A
^
∥
X
(
1
)
−
A
^
(
C
⊙
B
)
T
∥
F
\min_{\hat{A}} \| X_{(1)} - \hat{A} (C \odot B)^{T} \|_{F}
A^min∥X(1)−A^(C⊙B)T∥F
其中
A
^
=
A
⋅
diag
(
λ
)
\hat{A} = A \cdot \text{diag}(\lambda)
A^=A⋅diag(λ),那么上述式子的最优解为:
A
^
=
X
(
1
)
[
(
C
⊙
B
)
T
]
†
\hat{A} = X_{(1)} [(C \odot B)^{T}]^{\dagger}
A^=X(1)[(C⊙B)T]†
为了防止数值计算的病态问题,通常将
A
^
\hat{A}
A^ 的每一列单位化,即
λ
r
=
∥
a
^
r
∥
\lambda_{r} = \| \hat{a}_{r} \|
λr=∥a^r∥,
a
r
=
a
^
r
/
λ
r
a_{r} = \hat{a}_{r} / \lambda_{r}
ar=a^r/λr。将上述式子推广到高阶形式,可以得到:
A
(
n
)
=
X
n
(
A
(
N
)
⨀
⋯
⨀
A
(
n
+
1
)
⨀
A
(
n
−
1
)
⋯
⨀
A
1
)
V
†
其中
V
=
A
(
1
)
T
(
A
(
1
)
⨀
⋯
⨀
A
(
n
−
1
)
⨀
A
(
n
+
1
)
⋯
⨀
A
(
N
)
T
A
(
N
)
)
\begin{aligned} & A^{(n)} = X^{n} (A^{(N)} \bigodot \dots \bigodot A^{(n+1)} \bigodot A^{(n-1)} \dots \bigodot A^{1}) V^{\dagger} \\ & \text{其中} \quad V = A^{(1)T} (A^{(1)} \bigodot \dots \bigodot A^{(n-1)} \bigodot A^{(n+1)} \dots \bigodot A^{(N)T} A^{(N)}) \end{aligned}
A(n)=Xn(A(N)⨀⋯⨀A(n+1)⨀A(n−1)⋯⨀A1)V†其中V=A(1)T(A(1)⨀⋯⨀A(n−1)⨀A(n+1)⋯⨀A(N)TA(N))
对于一个
N
N
N 阶张量
X
X
X,其 ALS 求解的步骤如下图所示。它假设分解出 Rank-1 张量的个数
R
R
R 是事先已知的。对于各个因子的初始化,可以采用随机初始化,也可以通过以下式子进行初始化:
A
(
n
)
=
R
leading left singular vectors of
X
(
n
)
for
n
=
1
,
…
,
N
A^{(n)} = R \quad \text{leading left singular vectors of} \ X_{(n)} \ \text{for} \ n=1,\dots,N
A(n)=Rleading left singular vectors of X(n) for n=1,…,N

可加约束
在一些应用中,为了使 CP 分解更加鲁棒和精确,可以在分解出的因子上加上一些先验知识,即约束。例如,平滑约束(smooth)、正交约束、非负约束(nonnegative)、稀疏约束(sparsity)等。
CP 分解应用
CP 分解已在信号处理、视频处理、语音处理、计算机视觉、机器学习等领域得到了广泛应用。以下以去噪为例,阐述 CP 分解在高光谱图像处理中的应用。
高光谱图像(HSI)是上个世纪 80 年代以来新兴的一种新型成像技术,它包括了可见光和不可见光范围的几十到几百个连续光谱窄波段,形成了一种数据立方体结构的图像。高光谱图像可以看作是一个三阶张量,图像的空间域和光谱域构成了数据的三个维度。采用低秩 CP 分解对高光谱图像去噪,认为低秩的部分是无噪声的部分,剩下的部分被认为是噪声数据,其示意图如下图所示:
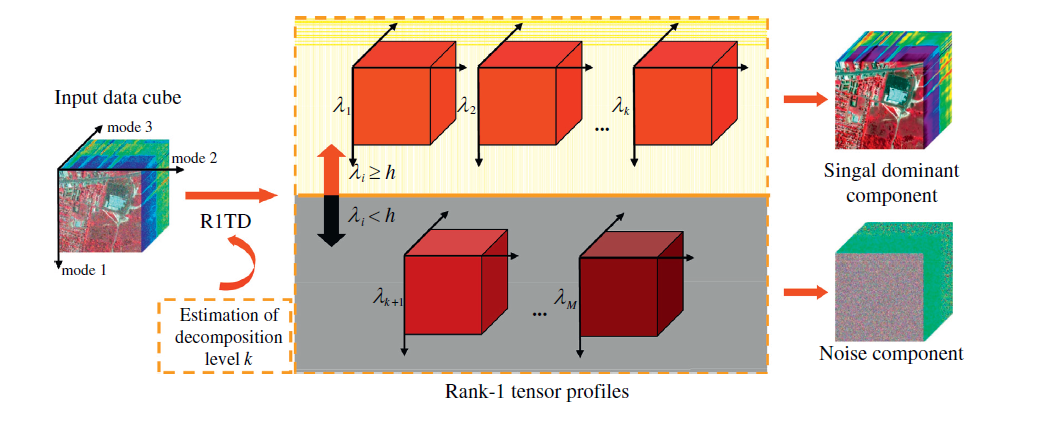
从图中可以看出,一个高光谱图像数据
X
\mathcal{X}
X 可以由两部分组成,即:
X
=
S
+
N
\mathcal{X} = \mathcal{S} + \mathcal{N}
X=S+N
其中,
S
\mathcal{S}
S 被认为是低秩的部分,即干净的图像;
N
\mathcal{N}
N 是噪声的部分(这里的噪声包括白噪声、高斯噪声等)。可以通过对原始数据
X
\mathcal{X}
X 进行低秩 CP 分解来得到
S
\mathcal{S}
S。在 Urban 数据上进行去噪,得到去噪前的数据和去噪之后的数据图分别如下图所示。从图中可以看出,采用 CP 分解可以对高光谱图像进行去噪。


张量分解 - Tucker 分解
Tucker 分解
Tucker 分解最早由 Tucker 在 1966 年提出。一个三阶张量的 Tucker 分解的图示如下图所示:
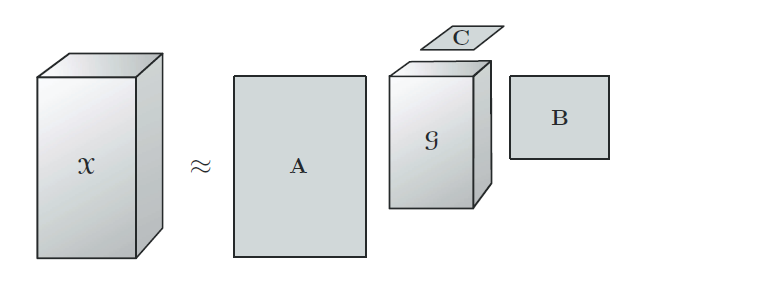
对于一个三阶张量 X ∈ R I × J × K \mathcal{X} \in \mathbb{R}^{I \times J \times K} X∈RI×J×K,Tucker 分解可以得到 A ∈ R I × P A \in \mathbb{R}^{I \times P} A∈RI×P、 B ∈ R J × Q B \in \mathbb{R}^{J \times Q} B∈RJ×Q、 C ∈ R K × R C \in \mathbb{R}^{K \times R} C∈RK×R 三个因子矩阵和一个核张量 G ∈ R P × Q × R \mathcal{G} \in \mathbb{R}^{P \times Q \times R} G∈RP×Q×R。每个 mode 上的因子矩阵称为张量在每个 mode 上的基矩阵或主成分,因此 Tucker 分解又称为高阶 PCA、高阶 SVD 等。从图中可以看出,CP 分解是 Tucker 分解的一种特殊形式:如果核张量的各个维数相同并且是对角的,则 Tucker 分解就退化成了 CP 分解。
在三阶张量形式中,有:
X
=
G
×
1
A
×
2
B
×
3
C
=
∑
p
=
1
P
∑
q
=
1
Q
∑
r
=
1
R
g
p
q
r
a
p
∘
b
q
∘
c
r
=
[
[
G
;
A
,
B
,
C
]
]
\mathcal{X} = \mathcal{G} \times_{1} A \times_{2} B \times_{3} C = \sum_{p=1}^{P} \sum_{q=1}^{Q} \sum_{r=1}^{R} g_{pqr} a_{p} \circ b_{q} \circ c_{r} = \left[\kern-0.15em\left[ \mathcal{G} ; A,B,C \right]\kern-0.15em\right]
X=G×1A×2B×3C=p=1∑Pq=1∑Qr=1∑Rgpqrap∘bq∘cr=[[G;A,B,C]]
将上述公式写成矩阵的形式为:
X
1
=
A
G
(
1
)
(
C
⊗
B
)
T
X
2
=
B
G
(
2
)
(
C
⊗
A
)
T
X
3
=
C
G
(
3
)
(
B
⊗
A
)
T
\begin{aligned} & X_{1} = A G_{(1)} (C \otimes B)^{T} \\ & X_{2} = B G_{(2)} (C \otimes A)^{T} \\ & X_{3} = C G_{(3)} (B \otimes A)^{T} \end{aligned}
X1=AG(1)(C⊗B)TX2=BG(2)(C⊗A)TX3=CG(3)(B⊗A)T
对于三阶张量,固定一个因子矩阵为单位阵,就得到 Tucker 分解的一个重要特例:Tucker2。例如,固定
C
=
I
C = I
C=I,则退化为:
X
=
G
×
1
A
×
2
B
=
[
[
G
;
A
,
B
,
I
]
]
\mathcal{X} = \mathcal{G} \times_{1} A \times_{2} B = \left[\kern-0.15em\left[ \mathcal{G} ; A,B,I \right]\kern-0.15em\right]
X=G×1A×2B=[[G;A,B,I]]
进一步地,如果固定两个因子矩阵,就得到了 Tucker1。例如,固定
C
=
I
C = I
C=I、
B
=
I
B = I
B=I,则 Tucker 分解就退化成了普通的 PCA:
X
=
G
×
1
A
=
[
[
G
;
A
,
I
,
I
]
]
\mathcal{X} = \mathcal{G} \times_{1} A = \left[\kern-0.15em\left[ \mathcal{G} ; A,I,I \right]\kern-0.15em\right]
X=G×1A=[[G;A,I,I]]
将上述公式推广到
N
N
N 阶的模型,即可得到:
X
=
G
×
1
A
(
1
)
×
2
A
(
2
)
⋯
×
(
N
)
A
(
N
)
=
[
[
G
;
A
(
1
)
,
A
(
2
)
,
…
,
A
(
N
)
]
]
\mathcal{X} = \mathcal{G} \times_{1} A^{(1)} \times_{2} A^{(2)} \cdots \times_{(N)} A^{(N)} = \left[\kern-0.15em\left[ \mathcal{G} ; A^{(1)}, A^{(2)}, \dots, A^{(N)} \right]\kern-0.15em\right]
X=G×1A(1)×2A(2)⋯×(N)A(N)=[[G;A(1),A(2),…,A(N)]]
写成矩阵形式为:
X
(
n
)
=
A
(
n
)
G
(
n
)
(
A
(
N
)
⊗
⋯
⊗
A
(
n
+
1
)
⊗
A
(
n
−
1
)
⋯
⊗
A
(
1
)
)
T
X_{(n)} = A^{(n)} G_{(n)} (A^{(N)} \otimes \dots \otimes A^{(n+1)} \otimes A^{(n-1)} \dots \otimes A^{(1)})^{T}
X(n)=A(n)G(n)(A(N)⊗⋯⊗A(n+1)⊗A(n−1)⋯⊗A(1))T
n n n-秩与低秩近似
n
n
n-秩又称为多线性秩。一个
N
N
N 阶张量
X
\mathcal{X}
X 的
n
n
n-mode 秩定义为:
rank
n
(
X
)
=
rank
(
X
(
n
)
)
\text{rank}_{n}(\mathcal{X}) = \text{rank}(X_{(n)})
rankn(X)=rank(X(n))
令
rank
n
(
X
)
=
R
n
\text{rank}_{n}(\mathcal{X}) = R_{n}
rankn(X)=Rn,
n
=
1
,
…
,
N
n = 1, \dots, N
n=1,…,N,则
X
\mathcal{X}
X 被称为秩
(
R
1
,
R
2
,
…
,
R
n
)
(R_{1}, R_{2}, \dots, R_{n})
(R1,R2,…,Rn) 的张量。
R
n
R_{n}
Rn 可以看作是张量
X
\mathcal{X}
X 在各个 mode 上 fiber 所构成的空间的维度。如果
rank
n
(
X
)
=
R
n
\text{rank}_{n}(\mathcal{X}) = R_{n}
rankn(X)=Rn,
n
=
1
,
…
,
N
n = 1, \dots, N
n=1,…,N,则很容易得到
X
\mathcal{X}
X 的一个精确秩
(
R
1
,
R
2
,
…
,
R
N
)
(R_{1}, R_{2}, \dots, R_{N})
(R1,R2,…,RN) Tucker 分解;然而,如果至少有一个
n
n
n 使得
rank
n
(
X
)
>
R
n
\text{rank}_{n}(\mathcal{X}) > R_{n}
rankn(X)>Rn,则通过 Tucker 分解得到的就是
X
\mathcal{X}
X 的一个秩
(
R
1
,
R
2
,
…
,
R
N
)
(R_{1}, R_{2}, \dots, R_{N})
(R1,R2,…,RN) 近似。下图展示了一个三阶张量的低秩近似,这在图像处理中可以认为是干净的图像:
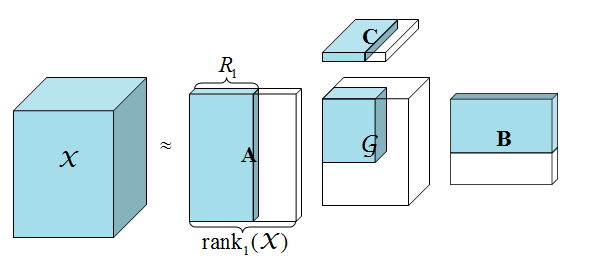
Tucker 分解的求解
对于固定的 n n n-秩,Tucker 分解的唯一性不能保证,一般加上一些约束,如分解得到的因子单位正交约束等。例如,HOSVD(High Order SVD)求解算法通过张量的每一个 mode 上做 SVD 分解对各个 mode 上的因子矩阵进行求解,最后计算张量在各个 mode 上的投影之后的张量作为核张量。其算法过程如下图所示:

虽然利用 SVD 对每个 mode 做一次 Tucker1 分解,但 HOSVD 不能保证得到一个较好的近似。然而,HOSVD 的结果可以作为其他迭代算法(如 HOOI)的一个很好的初始化。HOOI(High-order Orthogonal Iteration)算法将张量分解看作是一个优化的过程,不断迭代得到分解结果。假设有一个
N
N
N 阶张量
X
∈
R
I
1
×
I
2
×
⋯
×
I
N
\mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}}
X∈RI1×I2×⋯×IN,那么对
X
\mathcal{X}
X 进行分解就是对以下问题进行求解:
∣
X
−
[
[
G
;
A
(
1
)
,
…
,
A
(
N
)
]
]
∣
=
∣
vec
(
X
)
−
(
A
(
N
)
⊗
⋯
⊗
A
(
1
)
)
vec
(
G
)
∣
\begin{aligned} & \left| \mathcal{X} - \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right| \\ = & \left| \text{vec}(\mathcal{X}) - \left( \mathbf{A}^{(N)} \otimes \dots \otimes \mathbf{A}^{(1)} \right) \text{vec}(\mathcal{G}) \right| \end{aligned}
=
X−[[G;A(1),…,A(N)]]
vec(X)−(A(N)⊗⋯⊗A(1))vec(G)
将上述目标函数进一步化简得到:
∥
X
−
[
[
G
;
A
(
1
)
,
…
,
A
(
N
)
]
]
∥
2
=
∥
X
∥
2
−
2
⟨
X
,
[
[
G
;
A
(
1
)
,
…
,
A
(
N
)
]
]
⟩
+
∥
[
[
G
;
A
(
1
)
,
…
,
A
(
N
)
]
]
∥
2
=
∥
X
∥
2
−
2
⟨
X
×
1
A
(
1
)
T
⋯
×
N
A
(
N
)
T
,
G
⟩
+
∥
G
∥
2
=
∥
X
∥
2
−
2
⟨
G
,
G
⟩
+
∥
G
∥
2
\begin{aligned} & \left\| \mathcal{X} - \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right\|^{2} \\ = & \left\| \mathcal{X} \right\|^{2} - 2 \left\langle \mathcal{X}, \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right\rangle + \left\| \left[\kern-0.15em\left[ \mathcal{G}; \mathbf{A}^{(1)}, \dots, \mathbf{A}^{(N)} \right]\kern-0.15em\right] \right\|^{2} \\ = & \left\| \mathcal{X} \right\|^{2} - 2 \left\langle \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T}, \mathcal{G} \right\rangle + \left\| \mathcal{G} \right\|^{2} \\ = & \left\| \mathcal{X} \right\|^{2} - 2 \left\langle \mathcal{G}, \mathcal{G} \right\rangle + \left\| \mathcal{G} \right\|^{2} \end{aligned}
===
X−[[G;A(1),…,A(N)]]
2∥X∥2−2⟨X,[[G;A(1),…,A(N)]]⟩+
[[G;A(1),…,A(N)]]
2∥X∥2−2⟨X×1A(1)T⋯×NA(N)T,G⟩+∥G∥2∥X∥2−2⟨G,G⟩+∥G∥2
而
G
\mathcal{G}
G 满足:
G
=
X
×
1
A
(
1
)
T
⋯
×
N
A
(
N
)
T
\mathcal{G} = \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T}
G=X×1A(1)T⋯×NA(N)T
从而可以得到:
∥
X
∥
2
−
∥
X
×
1
A
(
1
)
T
⋯
×
N
A
(
N
)
T
∥
2
\left\| \mathcal{X} \right\|^{2} - \left\| \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T} \right\|^{2}
∥X∥2−
X×1A(1)T⋯×NA(N)T
2
由于
∥
X
∥
\|\mathcal{X}\|
∥X∥ 是一个常数,最小化上述式子相当于最大化:
max
∥
X
×
1
A
(
1
)
T
⋯
×
N
A
(
N
)
T
∥
subject to
A
(
n
)
∈
R
I
n
×
R
n
and
columnwise orthogonal
\begin{aligned} & \max \left\| \mathcal{X} \times_{1} \mathbf{A}^{(1)T} \cdots \times_{N} \mathbf{A}^{(N)T} \right\| \\ \text{subject to} \quad & \mathbf{A}^{(n)} \in \mathbb{R}^{I_{n} \times R_{n}} \quad \text{and} \quad \text{columnwise orthogonal} \end{aligned}
subject tomax
X×1A(1)T⋯×NA(N)T
A(n)∈RIn×Rnandcolumnwise orthogonal
写成矩阵形式为:
max
∥
A
(
n
)
T
W
∥
s.t.
W
=
X
(
n
)
(
A
(
N
)
⊗
⋯
⊗
A
(
n
+
1
)
⊗
A
(
n
−
1
)
⋯
⊗
A
(
1
)
)
\begin{aligned} & \max \left\| \mathbf{A}^{(n)T} \mathbf{W} \right\| \\ \text{s.t.} \quad & \mathbf{W} = \mathbf{X}_{(n)} \left( \mathbf{A}^{(N)} \otimes \dots \otimes \mathbf{A}^{(n+1)} \otimes \mathbf{A}^{(n-1)} \dots \otimes \mathbf{A}^{(1)} \right) \end{aligned}
s.t.max
A(n)TW
W=X(n)(A(N)⊗⋯⊗A(n+1)⊗A(n−1)⋯⊗A(1))
这个问题可以通过令
A
(
n
)
\mathbf{A}^{(n)}
A(n) 为
W
W
W 的前
R
n
R_{n}
Rn 个左奇异值向量来进行求解。HOOI 算法的过程如下图所示:

约束 Tucker 分解
除了可以在 Tucker 分解的各个因子矩阵上加上正交约束以外,还可以加一些其他约束,比如稀疏约束、平滑约束、非负约束等。另外,在一些应用场景中,不同 mode 的物理意义不同,可以加上不同的约束。在下图中,在三个不同的 mode 上分别加上了正交约束、非负约束以及统计独立性约束等:
Tucker 分解的应用
前面提到,Tucker 分解可以看作是 PCA 的多线性版本,因此可以用于数据降维、特征提取、张量子空间学习等。例如,一个低秩的张量近似可以用于去噪操作等。Tucker 分解同时在高光谱图像中也有所应用,如用低秩 Tucker 分解进行高光谱图像的去噪,用张量子空间进行高光谱图像的特征选择,用 Tucker 分解进行数据的压缩等。以下以高光谱图像去噪为例进行介绍。Decomposable Nonlocal Tensor Dictionary Learning for Multispectral Image Denoising 中对高光谱图像去噪的流程如下图所示:
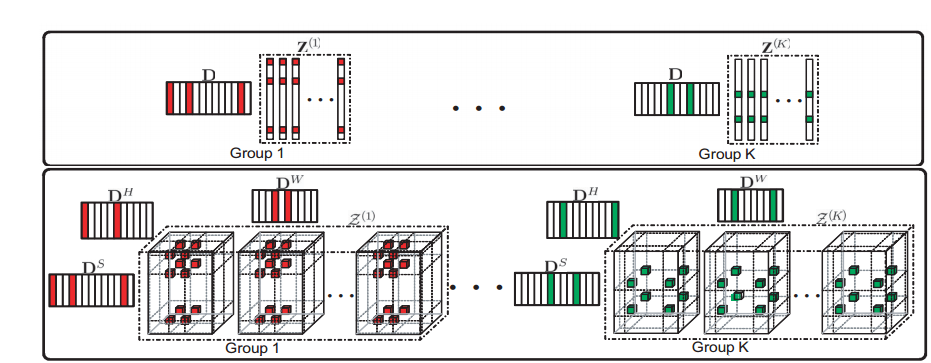
它首先对高光谱图像进行分块,然后对分块进行聚类,得到一些 group,最后对各个 group 里面的数据进行低秩 Tucker 分解。处理之前的噪声图像和处理之后的图像的对比如下图所示,可以发现 Tucker 分解可以对高光谱数据进行有效的去噪处理:


张量分解 - Block Term Decomposition (BTD)
去年差不多这个时候,我在本人的博客上发表了三篇关于张量分解的博客,从百度统计来看,很多人阅读了这三篇博文。今天,我再介绍一种张量分解 - Block Term Decomposition (BTD),以下将分几个部分对 BTD 进行介绍。
从 CP 分解到 BTD
在 CP 分解中,我们将一个张量分解为
K
K
K 个 Rank-1 的成员张量的形式,写成公式即为:
T
=
∑
r
=
1
K
a
r
∘
b
r
∘
c
r
=
∑
r
=
1
K
(
a
r
b
r
T
)
∘
c
r
\mathcal{T} = \sum_{r=1}^{K} a_{r} \circ b_{r} \circ c_{r} = \sum_{r=1}^{K} (a_{r} b_{r}^{T}) \circ c_{r}
T=r=1∑Kar∘br∘cr=r=1∑K(arbrT)∘cr
显然,
a
r
b
r
T
a_{r} b_{r}^{T}
arbrT 是一个 Rank-1 的矩阵,即一个低秩矩阵。而低秩往往是一些局部的特征,例如人的眉毛通常是低秩的。然而,在一些应用中,我们希望得到不同秩的特征,或者是不同尺度的特征,例如对于人脸,我们希望得到鼻子、眉毛、嘴巴、脸型等特征,此时 CP 分解就无法直观地做到。
基于 CP 分解,我们设想,如果
a
r
b
r
T
a_{r} b_{r}^{T}
arbrT 不是一个秩为 1 的矩阵,而是一个秩为
L
r
L_{r}
Lr 的矩阵,那么显然
a
r
a_{r}
ar 和
b
r
b_{r}
br 就不是一个向量,而是一个秩为
L
r
L_{r}
Lr 的矩阵。于是得到了 BTD 模型的一种形式:
T
=
∑
r
=
1
K
A
r
B
r
T
∘
c
r
\mathcal{T} = \sum_{r=1}^{K} A_{r} B_{r}^{T} \circ c_{r}
T=r=1∑KArBrT∘cr
可以将这个模型进一步推导,得到 BTD 的通俗形式。
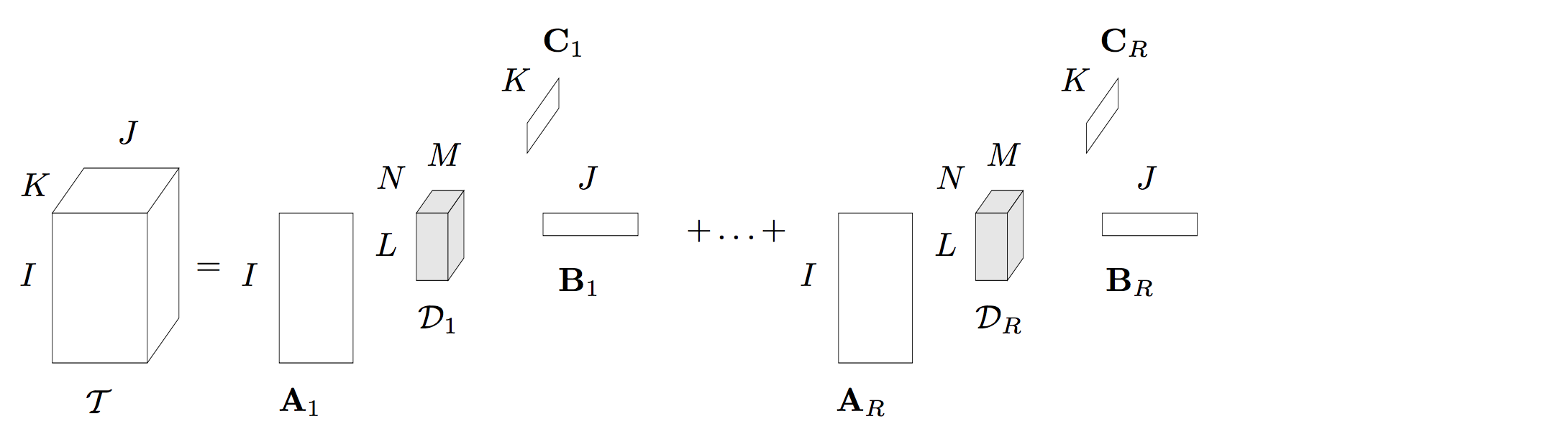
BTD 分解概览
2008 年,Lieven De Lathauwer 等人提出了一种 Block Term Decomposition(BTD),这种张量分解在一些论文中也被称为 Block Component Decomposition (BCD)。本人认为叫 BCD 更合理一些,因为这种张量分解将一个 N N N 阶张量分解为 R R R 个成员张量的形式,BCD 更符合。如下图就是一个 Rank − ( L r , M r , N r ) \text{Rank}-(L_{r}, M_{r}, N_{r}) Rank−(Lr,Mr,Nr) 的分解,每一个成员张量是一个 Rank − ( L r , M r , N r ) \text{Rank}-(L_{r}, M_{r}, N_{r}) Rank−(Lr,Mr,Nr) 的 Tucker 分解:
采用数学表达式可以写为:
T
=
∑
r
=
1
R
D
r
×
1
A
r
×
2
B
r
×
3
C
r
\mathcal{T} = \sum_{r=1}^{R} \mathcal{D}_{r} \times_{1} A_{r} \times_{2} B_{r} \times_{3} C_{r}
T=r=1∑RDr×1Ar×2Br×3Cr
其中
D
r
\mathcal{D}_{r}
Dr 是一个
Rank
−
(
L
r
,
M
r
,
N
r
)
\text{Rank}-(L_{r}, M_{r}, N_{r})
Rank−(Lr,Mr,Nr) 的张量,
A
r
∈
R
I
×
L
A_{r} \in \mathbb{R}^{I \times L}
Ar∈RI×L 是一个秩为
I
I
I 的矩阵。显然,BTD 分解可以看作是之前介绍的 Tucker 分解和 CP 分解的结合形式。当
R
=
1
R = 1
R=1 时,显然成员张量只有一个,此时这个分解就是一个
Rank
−
(
L
,
M
,
N
)
\text{Rank}-(L, M, N)
Rank−(L,M,N) 的 Tucker 分解。而当每一个成员张量是一个
Rank
−
1
\text{Rank}-1
Rank−1 分解时,该分解退化为一个 CP 分解(CP 分解是将一个张量分解为
R
R
R 个秩为 1 的张量分解形式)。这也说明了,BTD 分解具有很强的泛化能力。论文 http://epubs.siam.org/doi/pdf/10.1137/070690730 同时对它的唯一性进行了证明,从证明来看,该算法的唯一性的条件要比 Tucker 分解和 CP 分解的唯一性要弱。
BTD 分解的求解
BTD 分解的求解算法有很多种,例如非线性最小二乘法 http://epubs.siam.org/doi/abs/10.1137/110832124,交替最小二乘算法(ALS),张量对角算法等。其中,交替最小二乘算法形式最为简单。以下以一个三阶张量 T ∈ R I × J × K \mathcal{T} \in \mathbb{R}^{I \times J \times K} T∈RI×J×K 为例,介绍这种求解算法。
定义
A
=
[
A
1
,
…
,
A
R
]
A = [A_{1}, \dots, A_{R}]
A=[A1,…,AR],
B
=
[
B
1
,
…
,
B
R
]
B = [B_{1}, \dots, B_{R}]
B=[B1,…,BR],
C
=
[
C
1
,
…
,
C
R
]
C = [C_{1}, \dots, C_{R}]
C=[C1,…,CR],将 BTD 写为矩阵的形式,可以得到如下三个表达式:
T
J
K
×
I
=
(
B
⊗
C
)
⋅
Blockdiag
(
D
1
M
N
×
L
,
…
,
D
R
M
N
×
L
)
A
T
T
K
I
×
J
=
(
C
⊗
A
)
⋅
Blockdiag
(
D
1
N
L
×
M
,
…
,
D
R
N
L
×
M
)
B
T
T
I
J
×
K
=
(
A
⊗
B
)
⋅
Blockdiag
(
D
1
L
M
×
N
,
…
,
D
R
L
M
×
N
)
C
T
\begin{aligned} & T_{JK \times I} = (B \otimes C) \cdot \text{Blockdiag}(\mathcal{D}_{1_{MN \times L}}, \dots, \mathcal{D}_{R_{MN \times L}}) A^{T} \\ & T_{KI \times J} = (C \otimes A) \cdot \text{Blockdiag}(\mathcal{D}_{1_{NL \times M}}, \dots, \mathcal{D}_{R_{NL \times M}}) B^{T} \\ & T_{IJ \times K} = (A \otimes B) \cdot \text{Blockdiag}(\mathcal{D}_{1_{LM \times N}}, \dots, \mathcal{D}_{R_{LM \times N}}) C^{T} \end{aligned}
TJK×I=(B⊗C)⋅Blockdiag(D1MN×L,…,DRMN×L)ATTKI×J=(C⊗A)⋅Blockdiag(D1NL×M,…,DRNL×M)BTTIJ×K=(A⊗B)⋅Blockdiag(D1LM×N,…,DRLM×N)CT
当更新某一个因子矩阵或张量时,固定其他元素即可进行求解。例如,当求解
A
A
A 时,固定
D
r
\mathcal{D}_{r}
Dr 和
B
B
B 以及
C
C
C,设置
M
=
(
B
⊗
C
)
⋅
Blockdiag
(
D
1
M
N
×
L
,
…
,
D
R
M
N
×
L
)
M = (B \otimes C) \cdot \text{Blockdiag}(\mathcal{D}_{1_{MN \times L}}, \dots, \mathcal{D}_{R_{MN \times L}})
M=(B⊗C)⋅Blockdiag(D1MN×L,…,DRMN×L),因此可以得到
A
A
A 的更新规则为:
A
=
M
†
T
J
K
×
I
A = M^{\dagger} T_{JK \times I}
A=M†TJK×I
同理可以得到其他矩阵或张量的更新规则。因此,采用 ALS 算法求解 BTD 的步骤如下图所示:

算法中的 QR 分解是为了防止算法出现数值计算错误。
特殊 BTD 分解
在前面已经介绍了 BTD 分解的两种特殊形式:Tucker 分解和 CP 分解。以下再介绍两种特殊的张量分解。
Rank- ( L r , L r , 1 ) (L_{r}, L_{r}, 1) (Lr,Lr,1) 分解
当每一个成员张量退化为 L r × L r L_{r} \times L_{r} Lr×Lr 的矩阵时,可以得到 Rank − ( L r , L r , 1 ) \text{Rank}-(L_{r}, L_{r}, 1) Rank−(Lr,Lr,1) 分解,即:
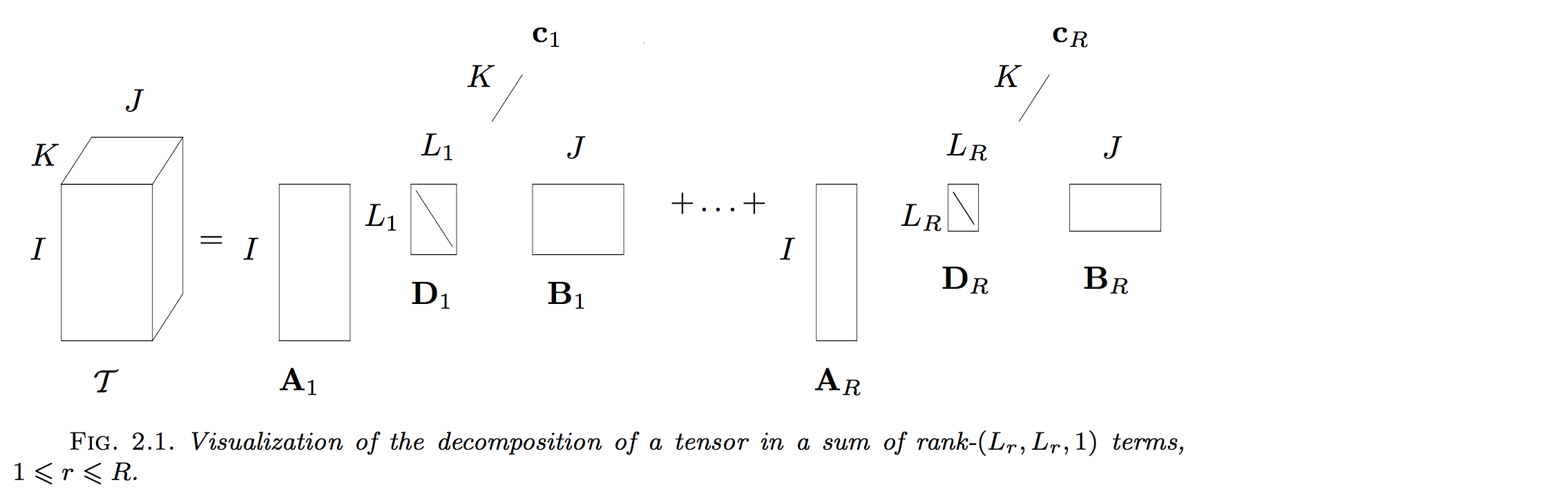
相应的求解算法与 BTD 算法类似,只是没有最后一步求解 core tensor 的部分:

Rank- ( L , L , 1 ) (L, L, 1) (L,L,1) 分解
当 Rank − ( L r , L r , 1 ) \text{Rank}-(L_{r}, L_{r}, 1) Rank−(Lr,Lr,1) 的每一个 L r L_{r} Lr 取值为一致,即 L L L 时,即可得到 Rank − ( L , L , 1 ) \text{Rank}-(L, L, 1) Rank−(L,L,1) 分解,即:

BTD 分解的应用
BTD 分解的现阶段主要应用在盲源分离上,尤其是它的蜕化形式 Rank − ( L , L , 1 ) \text{Rank}-(L, L, 1) Rank−(L,L,1) 形式。在 Rank − ( L , L , 1 ) \text{Rank}-(L, L, 1) Rank−(L,L,1) 中, c r c_{r} cr 可以看作是一个信号, A r × B r A_{r} \times B_{r} Ar×Br 可以看作是混合矩阵的低秩表达形式。本人也基于此分解在 IEEE TGRS 上发表了一篇题为 “Matrix-Vector Nonnegative Tensor Factorization for Blind Unmixing of Hyperspectral Imagery” 的文章。
此外,BTD 分解现在也开始应用在深度学习中(事实上,张量分解在深度学习中的应用最近被广泛研究,因为张量分解可以有效地减少深度学习中参数的个数,具体可以参考相关文献)。新加坡国立大学颜水成教授 2017 年发表了一篇题为 Sharing Residual Units Through Collective Tensor Factorization in Deep Neural Networks 的文章,这篇文章中,用 BTD 分解来代替残差网络中的卷积单元(尚未仔细阅读,待详细研究后补充):
Figure 1. Convolution kernel approximation by different approaches.
图 1. 不同方法的卷积核近似。(a) A full rank convolution layer with a kernel size of w × h w \times h w×h.
一个具有 w × h w \times h w×h 核大小的全秩卷积层。
(b) An approximation of (a) by using the low-rank Tucker Decomposition (a special case of Block Term Decomposition when R = 1 R = 1 R=1).
使用低秩 Tucker 分解(当 R = 1 R = 1 R=1 时,块项分解的特例)对 (a) 进行近似。
© An approximation of (a) by using low-rank Block Term Decomposition. The new proposed CRU shares the first two layers (yellow) across different residual functions.
使用低秩块项分解对 (a) 进行近似。新提出的 CRU 在不同的残差函数中共享前两层(黄色)。
via:
- 张量分解-张量介绍
https://www.xiongfuli.com/机器学习/2016-06/tensor-decomposition-part1.html - 张量分解-CP分解
https://www.xiongfuli.com/机器学习/2016-06/tensor-decomposition-cp.html - 张量分解-Tucker分解
https://www.xiongfuli.com/机器学习/2016-06/tensor-decomposition-tucker.html - 张量分解-Block term decomposition (BTD)
https://www.xiongfuli.com/机器学习/2017-06/tensor-decomposition-BTD.html






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








