注:本文为 “标量、向量、矩阵和张量的区别” 相关合辑。
英文引文,机翻未校。
如有内容异常,请看原文。
Difference Between Scalar, Vector, Matrix and Tensor
标量、向量、矩阵和张量的区别
Last Updated : 06 Aug, 2025
In the context of mathematics and machine learning, scalar, vector, matrix, and tensor are all different types of mathematical objects that represent different concepts and have different properties. Here in this article, we will discuss in detail scalars, vectors, matrixes, tensors, and finally the differences between them.
在数学和机器学习的背景下,标量、向量、矩阵和张量是不同类型的数学对象,它们代表不同的概念并具有不同的属性。在本文中,我们将详细讨论标量、向量、矩阵、张量以及它们之间的区别。
What is Scalar?
什么是标量?
-
Scalars are singular numerical entities within the realm of Data Science, devoid of any directional attributes.
在数据科学领域,标量是单一的数值实体,没有任何方向属性。 -
They serve as the elemental components utilized in mathematical computations and algorithmic frameworks across these domains. In practical terms, scalars often represent fundamental quantities such as constants, probabilities, or error metrics.
它们是这些领域中用于数学计算和算法框架的基本组件。在实际中,标量通常表示基本量,例如常数、概率或误差指标。 -
For instance, within Machine Learning, a scalar may denote the accuracy of a model or the value of a loss function. Similarly, in Data Science, scalars are employed to encapsulate statistical metrics like mean, variance, or correlation coefficients. Despite their apparent simplicity, scalars assume a critical role in various AI-ML-DS tasks, spanning optimization, regression analysis, and classification algorithms. Proficiency in understanding scalars forms the bedrock for comprehending more intricate concepts prevalent in these fields.
例如,在机器学习中,标量可以表示模型的准确率或损失函数的值。同样,在数据科学中,标量用于封装诸如均值、方差或相关系数等统计指标。尽管标量看起来很简单,但它们在各种人工智能 - 机器学习 - 数据科学任务中起着关键作用,涵盖优化、回归分析和分类算法。掌握标量的理解是理解这些领域中更复杂概念的基础。 -
In Python we can represent a Scalar like:
在 Python 中,我们可以这样表示标量:# Scalars can be represented simply as numerical variables // 标量可以简单地表示为数值变量 scalar = 8.4 scalarOutput:
输出:8.4
What are Vectors?
什么是向量?
-
Vectors, within the context of Data Science, represent ordered collections of numerical values endowed with both magnitude and directionality. They serve as indispensable tools for representing features, observations, and model parameters within AI-ML-DS workflows.
在数据科学的背景下,向量是具有大小和方向的数值有序集合的表示。它们是人工智能 - 机器学习 - 数据科学工作流中用于表示特征、观测值和模型参数的不可或缺的工具。 -
In Artificial Intelligence, vectors find application in feature representation, where each dimension corresponds to a distinct feature of the dataset.
在人工智能中,向量用于特征表示,其中每个维度对应数据集的一个不同特征。 -
In Machine Learning, vectors play a pivotal role in encapsulating data points, model parameters, and gradient computations during the training process. Moreover, within DS, vectors facilitate tasks like data visualization, clustering, and dimensionality reduction. Mastery over vector concepts is paramount for engaging in activities like linear algebraic operations, optimization via gradient descent, and the construction of complex neural network architectures.
在机器学习中,向量在封装数据点、模型参数以及训练过程中的梯度计算方面发挥着关键作用。此外,在数据科学中,向量有助于数据可视化、聚类和降维等任务。掌握向量概念对于进行线性代数运算、通过梯度下降进行优化以及构建复杂神经网络架构等活动至关重要。 -
In Python we can represent a Vector like:
在 Python 中,我们可以这样表示向量:import numpy as np # Vectors can be represented as one-dimensional arrays // 向量可以表示为一维数组 vector = np.array([2, -3, 1.5]) vectorOutput:
输出:array([ 2. , -3. , 1.5])
What are Matrices?
什么是矩阵?
-
Matrices, as two-dimensional arrays of numerical values, enjoy widespread utility across AI-ML-DS endeavors. They serve as foundational structures for organizing and manipulating tabular data, wherein rows typically represent observations and columns denote features or variables.
作为数值的二维数组,矩阵在人工智能 - 机器学习 - 数据科学领域中被广泛使用。它们是组织和操作表格数据的基础结构,其中行通常表示观测值,列表示特征或变量。 -
Matrices facilitate a plethora of statistical operations, including matrix multiplication, determinant calculation, and singular value decomposition.
矩阵促进了包括矩阵乘法、行列式计算和奇异值分解在内的大量统计运算。 -
In the domain of AI, matrices find application in representing weight matrices within neural networks, with each element signifying the synaptic connection strength between neurons. Similarly, within ML, matrices serve as repositories for datasets, building kernel matrices for support vector machines, and implementing dimensionality reduction techniques such as principal component analysis. Within DS, matrices are indispensable for data preprocessing, transformation, and model assessment tasks.
在人工智能领域,矩阵用于表示神经网络中的权重矩阵,其中每个元素表示神经元之间的突触连接强度。同样,在机器学习中,矩阵作为数据集的存储库,用于构建支持向量机的核矩阵以及实现主成分分析等降维技术。在数据科学中,矩阵对于数据预处理、转换和模型评估任务是不可或缺的。 -
In Python we can represent a Matrix like:
在 Python 中,我们可以这样表示矩阵:import numpy as np # Matrices can be represented as two-dimensional arrays // 矩阵可以表示为二维数组 matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])Output:
输出:array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
What are Tensors?
什么是张量?
-
Tensors in Data Science generalize the concept of vectors and matrices to higher dimensions. They are multidimensional arrays of numerical values which can constitute complex data structures and relationships.
在数据科学中,张量将向量和矩阵的概念推广到更高维度。它们是数值的多维数组,可以构成复杂的数据结构和关系。 -
Tensors are integral in deep learning frameworks like TensorFlow and PyTorch, in which they may be used to store and manipulate multi-dimensional data such as images, videos, and sequences.
张量是深度学习框架(如 TensorFlow 和 PyTorch)的重要组成部分,它们可用于存储和操作多维数据,例如图像、视频和序列。 -
In AI, tensors are employed for representing input data, model parameters, and intermediate activations in neural networks. In ML, tensors facilitate operations in convolutional neural networks, recurrent neural networks, and transformer architectures. Moreover, in DS, tensors are utilized for multi-dimensional data analysis, time - series forecasting, and natural language processing tasks. Understanding tensors is crucial for advanced AI-ML-DS practitioners, as they allow the modeling and analysis of intricate data patterns and relationships across multiple dimensions.
在人工智能中,张量用于表示神经网络中的输入数据、模型参数和中间激活。在机器学习中,张量有助于卷积神经网络、循环神经网络和变换器架构中的操作。此外,在数据科学中,张量用于多维数据分析、时间序列预测和自然语言处理任务。对于高级人工智能 - 机器学习 - 数据科学从业者来说,理解张量至关重要,因为它们允许对多维度中的复杂数据模式和关系进行建模和分析。 -
In Python we can represent a Tensor like:
在 Python 中,我们可以这样表示张量:import numpy as np # Tensors can be represented as multi-dimensional arrays // 张量可以表示为多维数组 tensor = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]]) tensorOutput:
输出:array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
Scalar Vs Vector Vs Matrix Vs Tensor
标量与向量与矩阵与张量
| Aspect | Scalar 标量 | Vector 向量 | Matrix 矩阵 | Tensor 张量 |
|---|---|---|---|---|
| Dimensionality 维度 | 0 | 1 | 2 | ≥ 3 |
| Representation 表示 | Single numerical value 单个数值 | Ordered array of values 有序值数组 | Two - dimensional array of values 二维值数组 | Multidimensional array of values 多维值数组 |
| Usage 用途 | Represent basic quantities 表示基本量 | Represent features, observations 表示特征、观测值 | Organize data in tabular format 以表格格式组织数据 | Handle complex data structures 处理复杂数据结构 |
| Examples 示例 | Error metrics, probabilities 误差指标、概率 | Feature vectors, gradients 特征向量、梯度 | Data matrices, weight matrices 数据矩阵、权重矩阵 | Image tensors, sequence tensors 图像张量、序列张量 |
| Manipulation 操作 | Simple arithmetic operations 简单算术运算 | Linear algebra operations 线性代数运算 | Matrix operations, linear transformations 矩阵运算、线性变换 | Tensor operations, deep learning operations 张量运算、深度学习运算 |
| Data Representation 数据表示 | Point in space 空间中的点 | Direction and magnitude in space 空间中的方向和大小 | Rows and columns in tabular format 表格格式中的行和列 | Multi - dimensional relationships 多维关系 |
| Applications 应用 | Basic calculations, statistical measures 基本计算、统计量 | Machine learning models, data representation 机器学习模型、数据表示 | Data manipulation, statistical analysis 数据操作、统计分析 | Deep learning, natural language processing 深度学习、自然语言处理 |
| Notation 符号表示 | Lowercase letters or symbols 小写字母或符号 | Boldface letters or arrows 粗体字母或箭头 | Uppercase boldface letters 大写粗体字母 | Boldface uppercase letters or indices 粗体大写字母或索引 |
Conclusion
结论
We can conclude that the understanding of scalars, vectors, matrices, and tensors is paramount in the fields of Data Science, as they serve as fundamental building blocks for mathematical representation, computation, and analysis of data and models. Scalars, representing single numerical values, play a foundational role in basic calculations and statistical measures. Vectors, with their magnitude and direction, enable the representation of features, observations, and model parameters, crucial for machine learning tasks. Matrices organize data in a tabular format, facilitating operations like matrix multiplication and linear transformations, essential for statistical analysis and machine learning algorithms. Tensors, extending the concept to higher dimensions, handle complex data structures and relationships, powering advanced techniques in deep learning and natural language processing. Mastery of these mathematical entities empowers practitioners to model and understand intricate data patterns and relationships, driving innovation and advancement in AI, ML, and DS domains.
我们可以得出结论,理解标量、向量、矩阵和张量在数据科学领域至关重要,因为它们是数据和模型的数学表示、计算和分析的基本构建块。标量,表示单个数值,在基本计算和统计量中起基础作用。具有大小和方向的向量,能够表示特征、观测值和模型参数,这对于机器学习任务至关重要。矩阵以表格格式组织数据,便于进行矩阵乘法和线性变换等操作,这对于统计分析和机器学习算法是必不可少的。张量将概念扩展到更高维度,处理复杂的数据结构和关系,推动深度学习和自然语言处理中的高级技术。掌握这些数学实体使从业者能够对复杂的数据模式和关系进行建模和理解,推动人工智能、机器学习和数据科学领域的创新和进步。
What’s the difference between a matrix and a tensor?
矩阵和张量有什么区别?
Aug 28,2017
Steven Steinke
There is a short answer to this question,so let’s start there.Then we can take a look at an application to get a little more insight.
这个问题有一个简短的答案,让我们从那里开始。然后我们可以看看一个应用,以获得更多的见解。
A matrix is a grid of
n
×
m
n \times m
n×m (say,
3
×
3
3 \times 3
3×3) numbers surrounded by brackets.We can add and subtract matrices of the same size,multiply one matrix with another as long as the sizes are compatible
(
(
n
×
m
)
×
(
m
×
p
)
=
n
×
p
)
((n \times m) \times (m \times p) = n \times p )
((n×m)×(m×p)=n×p),and multiply an entire matrix by a constant.A vector is a matrix with just one row or column (but see below).So there are a bunch of mathematical operations that we can do to any matrix.
矩阵是一个由括号包围的
n
×
m
n \times m
n×m(比如说,
3
×
3
3 \times 3
3×3)数字网格。我们可以对相同大小的矩阵进行加法和减法运算,只要大小兼容
(
(
n
×
m
)
×
(
m
×
p
)
=
n
×
p
)
((n \times m) \times (m \times p) = n \times p )
((n×m)×(m×p)=n×p),就可以将一个矩阵与另一个矩阵相乘,还可以将整个矩阵乘以一个常数。向量是一个只有一行或一列的矩阵(但见下文)。因此,我们可以对任何矩阵进行许多数学运算。
The basic idea,though,is that a matrix is just a 2 - D grid of numbers.
然而,基本的想法是,矩阵只是一个二维数字网格。
A tensor is often thought of as a generalized matrix.That is,it could be a 1 - D matrix (a vector is actually such a tensor),a 3 - D matrix (something like a cube of numbers),even a 0 - D matrix (a single number),or a higher dimensional structure that is harder to visualize.The dimension of the tensor is called its rank.
张量通常被认为是一种广义矩阵。也就是说,它可以是一个一维矩阵(向量实际上就是这样的张量)、一个三维矩阵(类似于一个数字立方体)、甚至是一个零维矩阵(一个单独的数字),或者是一个更难可视化的更高维结构。张量的维度被称为它的秩。
But this description misses the most important property of a tensor!
但这种描述遗漏了张量最重要的属性!
A tensor is a mathematical entity that lives in a structure and interacts with other mathematical entities.If one transforms the other entities in the structure in a regular way,then the tensor must obey a related transformation rule.
张量是一种生活在结构中并与其他数学实体相互作用的数学实体。如果以一种规律的方式转换结构中的其他实体,那么张量必须遵循相关的转换规则。
This "dynamical"property of a tensor is the key that distinguishes it from a mere matrix.It’s a team player whose numerical values shift around along with those of its teammates when a transformation is introduced that affects all of them.
这种张量的“动态”属性是区分它与普通矩阵的关键。它是一个团队合作者,当引入影响它们所有人的转换时,它的数值会随着队友的数值而变化。
Any rank - 2 tensor can be represented as a matrix,but not every matrix is really a rank - 2 tensor.The numerical values of a tensor’s matrix representation depend on what transformation rules have been applied to the entire system.
任何二阶张量都可以表示为矩阵,但并非每个矩阵都是真正的二阶张量。张量的矩阵表示的数值取决于已应用于整个系统的转换规则。
This answer might be enough for your purposes,but we can do a little example to illustrate how this works.The question came up in a Deep Learning workshop,so let’s look at a quick example from that field.
这个答案可能足以满足你的需求,但我们可以做一个小例子来说明这是如何工作的。这个问题是在一个深度学习研讨会上提出的,因此让我们看看该领域的快速示例。
Suppose I have a hidden layer of 3 nodes in a neural network.Data flowed into them,went through their ReLU functions,and out popped some values.Let’s say,for definiteness,we got 2.5,4,and 1.2,respectively.(Don’t worry,a diagram is coming.)We could represent these nodes’ output as a vector,
假设我在一个神经网络中有一个包含 3 个节点的隐藏层。数据流入它们,经过它们的 ReLU 函数,然后弹出一些值。为了明确起见,我们得到了 2.5、4 和 1.2。(别担心,图表马上就会出现。)我们可以用一个向量来表示这些节点的输出,
L 1 = [ 2.5 4 1.2 ] {{L}_{1}}=\left[ \begin{matrix} 2.5 \\ 4 \\ 1.2 \\\end{matrix} \right] L1= 2.541.2
Let’s say there’s another layer of 3 nodes coming up.Each of the 3 nodes from the first layer has a weight associated with its input to each of the next 3 nodes.It would be very convenient,then,to write these weights as a
3
×
3
3 \times 3
3×3 matrix of entries.Suppose we’ve updated the network already many times and arrived at the weights (chosen semi - randomly for this example),
假设接下来还有一个包含 3 个节点的层。第一层的每个 3 个节点都有一个权重与其输入到下一层的每个 3 个节点相关联。那么,将这些权重写成一个
3
×
3
3 \times 3
3×3 的矩阵条目将非常方便。假设我们已经多次更新了网络,并得到了权重(为了这个例子半随机选择的),
W 12 = [ − 1 0.4 1.5 0.8 0.5 0.75 0.2 − 0.3 1 ] {{W}_{12}}=\left[ \begin{matrix} -1 & 0.4 & 1.5 \\ 0.8 & 0.5 & 0.75 \\ 0.2 & -0.3 & 1 \\ \end{matrix} \right] W12= −10.80.20.40.5−0.31.50.751
Here,the weights from one row all go to the same node in the next layer,and those in a particular column all come from the same node in the first layer.For example,the weight that incoming node 1 contributes to outgoing node 3 is 0.2 (row 3,col 1).
在这里,一行中的权重都流向下一层次的同一个节点,而特定列中的权重都来自第一层的同一个节点。例如,输入节点 1 对输出节点 3 的贡献权重是 0.2(第 3 行,第 1 列)。
We can compute the total values fed into the next layer of nodes by multiplying the weight matrix by the input vector,
我们可以通过将权重矩阵乘以输入向量来计算输入到下一层节点的总值,
W 12 L 1 = L 2 → [ − 1 0.4 1.5 0.8 0.5 0.75 0.2 − 0.3 1 ] [ 2.5 4 1.2 ] = [ 0.9 4.9 0.5 ] {{W}_{12}}{{L}_{1}}={{L}_{2}}\to \left[ \begin{matrix} -1 & 0.4 & 1.5 \\ 0.8 & 0.5 & 0.75 \\ 0.2 & -0.3 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} 2.5 \\ 4 \\ 1.2 \\ \end{matrix} \right]=\left[ \begin{matrix} 0.9 \\ 4.9 \\ 0.5 \\ \end{matrix} \right] W12L1=L2→ −10.80.20.40.5−0.31.50.751 2.541.2 = 0.94.90.5
Don’t like matrices?Here’s a diagram.The data flow from left to right.
不喜欢矩阵?这里有一个图表。数据从左向右流动。
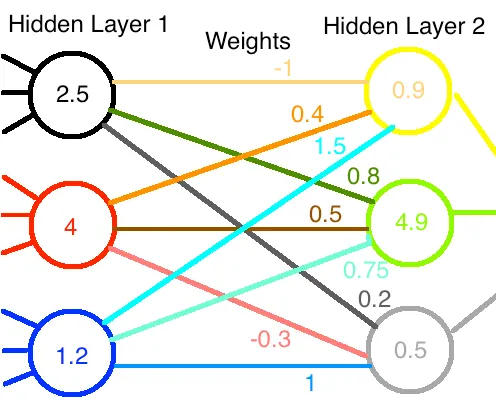
Great! So far,all we have seen are some simple manipulations of matrices and vectors.
太好了!到目前为止,我们看到的都是一些矩阵和向量的简单操作。
Suppose I want to meddle around and use custom activation functions for each neuron.A dumb way to do this would be to rescale each of the ReLU functions from the first layer individually.For the sake of this example,let’s suppose I scale the first node up by a factor of 2,leave the second node alone,and scale the third node down by 1/5.This would change the graphs of these functions as pictured below:
假设我想干预一下,为每个神经元使用自定义激活函数。一个愚蠢的方法是分别重新调整第一层的每个 ReLU 函数的大小。为了这个例子,假设我将第一个节点的大小增加 2 倍,保持第二个节点不变,并将第三个节点缩小 1/5。这将改变这些函数的图表,如下图所示:
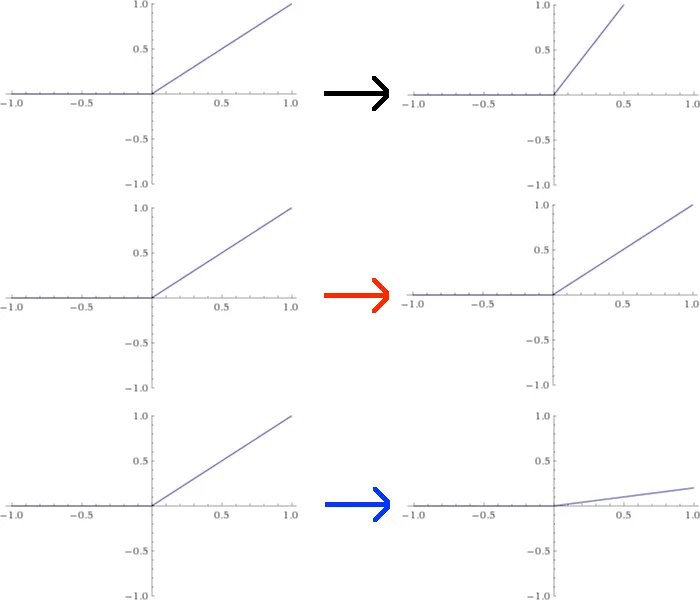
The effect of this modification is to change the values spit out by the first layer by factors of 2, 1, and 1/5, respectively. That’s equivalent to multiplying
L
1
L_1
L1 by a matrix
A
A
A ,
这种修改的效果是将第一层输出的值分别按 2、1 和 1/5 的比例进行改变。这相当于将
L
1
L_1
L1 乘以一个矩阵
A
A
A ,
A L 1 = L 1 ′ → [ 2 0 0 0 1 0 0 0 0.2 ] [ 2.5 4 1.2 ] = [ 5 4 0.24 ] A{{L}_{1}}={{L}_{1}}^{'}\to \left[ \begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0.2 \\ \end{matrix} \right]\left[ \begin{matrix} 2.5 \\ 4 \\ 1.2 \\ \end{matrix} \right]=\left[ \begin{matrix} 5 \\ 4 \\ 0.24 \\ \end{matrix} \right] AL1=L1′→ 200010000.2 2.541.2 = 540.24
Now,if these new values are fed through the original network of weights,we get totally different output values,as illustrated in the diagram:
现在,如果将这些新值通过原始权重网络,我们将得到完全不同的输出值,如图所示:
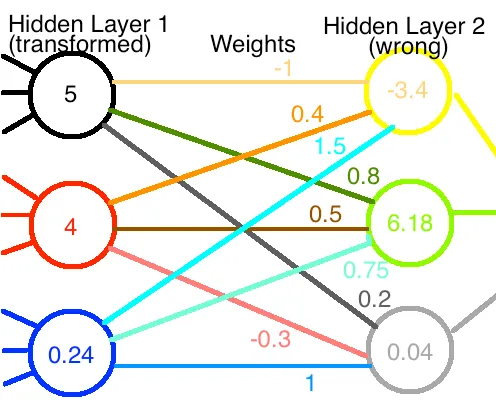
If the neural network were functioning properly before,we’ve broken it now.We’ll have to rerun the training to get the correct weights back.
如果神经网络之前运行正常,我们现在破坏了它。我们将不得不重新运行训练以恢复正确的权重。
Or will we?
还是这样吗?
The value at the first node is twice as big as before.If we cut all of its outgoing weights by 1/2,its net contribution to the next layer is unchanged.We didn’t do anything to the second node,so we can leave its weights alone.Lastly,we’ll need to multiply the final set of weights by 5 to compensate for the 1/5 factor on that node.This is equivalent,mathematically speaking,to using a new set of weights which we obtain by multiplying the original weight matrix by the inverse matrix of
A
A
A :
第一个节点的值是之前的两倍。如果我们将其所有输出权重减半,它对下一层的净贡献保持不变。我们没有对第二个节点做任何事情,所以我们可以保留其权重不变。最后,我们需要将最终一组权重乘以 5,以补偿该节点的 1/5 因子。从数学上讲,这相当于使用一组新的权重,我们通过将原始权重矩阵乘以
A
A
A 的逆矩阵来获得:
W 12 A − 1 = W 12 ′ [ − 1 0.4 1.5 0.8 0.5 0.75 0.2 − 0.3 1 ] [ 0.5 0 0 0 1 0 0 0 5 ] = [ − 0.5 0.4 7.5 0.4 0.5 3.75 0.1 − 0.3 5 ] {{W}_{12}}{{A}^{-1}}={{W}_{12}}^{'}\left[ \begin{matrix} -1 & 0.4 & 1.5 \\ 0.8 & 0.5 & 0.75 \\ 0.2 & -0.3 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} 0.5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 5 \\ \end{matrix} \right]=\left[ \begin{matrix} -0.5 & 0.4 & 7.5 \\ 0.4 & 0.5 & 3.75 \\ 0.1 & -0.3 & 5 \\ \end{matrix} \right] W12A−1=W12′ −10.80.20.40.5−0.31.50.751 0.500010005 = −0.50.40.10.40.5−0.37.53.755
If we combine the modified output of the first layer with the modified weights,we end up with the correct values reaching the second layer:
如果我们把第一层修改后的输出和修改后的权重结合起来,我们就会得到到达第二层的正确值:

Hurray!The network is working again,despite our best efforts to the contrary!
太好了!尽管我们尽力破坏,但网络又开始工作了!
OK,there’s been a ton of math,so let’s just sit back for a second and recap.
好吧,已经有很多数学内容了,让我们稍作休息,回顾一下。
When we thought of the node inputs,outputs and weights as fixed quantities,we called them vectors and matrices and were done with it.
当我们把节点输入、输出和权重视为固定量时,我们称它们为向量和矩阵,然后就结束了。
But once we started monkeying around with one of the vectors,transforming it in a regular way,we had to compensate by transforming the weights in an opposite manner.This added,integrated structure elevates the mere matrix of numbers to a true tensor
但一旦我们开始以一种规律的方式调整其中一个向量,我们就必须通过以相反的方式转换权重来进行补偿。这种增加的、整合的结构将单纯的数字矩阵提升为真正的张量。
In fact,we can characterize its tensor nature a little bit further.If we call the changes made to the nodes covariant (ie,varying with the node and multiplied by
A
A
A ),that makes the weights a contravariant tensor (varying against the nodes,specifically,multiplied by the inverse of
A
A
A instead of
A
A
A itself).A tensor can be covariant in one dimension and contravariant in another,but that’s a tale for another time.
事实上,我们可以进一步描述它的张量特性。如果我们把对节点所做的改变称为协变的(即,与节点一起变化并乘以
A
A
A ),那么这就使得权重成为一个逆变张量(与节点相反变化,具体来说,乘以
A
A
A 的逆矩阵而不是
A
A
A 本身)。张量可以在一个维度上是协变的,在另一个维度上是逆变的,但这是另一个故事了。
And now you know the difference between a matrix and a tensor.
现在你知道矩阵和张量的区别了。
What are the Differences Between a Matrix and a Tensor?
矩阵与张量的区别是什么?
asked Jun 5, 2013 at 21:52 Aurelius
What is the difference between a matrix and a tensor? Or, what makes a tensor, a tensor? I know that a matrix is a table of values, right? But, a tensor?
矩阵和张量的区别是什么?或者说,是什么让一个张量成为张量?我知道矩阵是一个数值表格,对吗?但张量呢?
Continuing with your analogy, a matrix is just a two-dimensional table to organize information and a tensor is just its generalization. You can think of a tensor as a higher-dimensional way to organize information. So a matrix (5x5 for example) is a tensor of rank 2. And a tensor of rank 3 would be a “3D-matrix” like a 5x5x5 matrix.
顺着你的类比来说,矩阵只是一个用于组织信息的二维表格,而张量是它的推广。你可以把张量看作是一种更高维度的信息组织方式。因此,一个矩阵(例如 5×5 的矩阵)是秩为 2 的张量。而秩为 3 的张量可以是一个“三维矩阵”,比如 5×5×5 的矩阵。
I thought a rank n tensor is multi-linear function which takes n vectors and returns a vector of the same vector space?
我认为 n 秩张量是一个多线性函数,它接收 n 个向量并返回同一个向量空间中的一个向量?
One point of confusion is that in machine learning, people often use the term “tensor” when they really mean just “multidimensional array”. I disagree that a tensor of rank 3 would be a “3D matrix”, but admittedly it’s not uncommon to hear the word “tensor” used in this way. (http://stats.stackexchange.com/questions/198061/why-the-sudden-fascination-with-tensors/198127)
一个容易混淆的点是,在机器学习中,人们经常使用“张量”这个术语,但实际上他们指的只是“多维数组”。我不认同秩为 3 的张量是“三维矩阵”这一说法,但不可否认,这种“张量”的用法并不少见。
Maybe to see the difference between rank 2 tensors and matrices, it is probably best to see a concrete example. Actually this is something which back then confused me very much in the linear algebra course (where we didn’t learn about tensors, only about matrices).
或许要理解秩为 2 的张量和矩阵之间的区别,最好看一个具体的例子。实际上,这是我当时在线性代数课程中(那门课我们没有学张量,只学了矩阵)非常困惑的事情。
As you may know, you can specify a linear transformation between vectors by a matrix. Let’s call that matrix
A
A
A. Now if you do a basis transformation, this can also be written as a linear transformation, so that if the vector in the old basis is
v
v
v, the vector in the new basis is
T
−
1
v
T^{-1}v
T−1v (where
v
v
v is a column vector). Now you can ask what matrix describes the transformation in the new basis. Well, it’s the matrix
T
−
1
A
T
T^{-1}AT
T−1AT.
如你所知,你可以用一个矩阵来表示向量之间的线性变换。我们称这个矩阵为
A
A
A。现在,如果你进行基变换,这也可以写成一个线性变换,因此,如果旧基下的向量是
v
v
v,那么新基下的向量是
T
−
1
v
T^{-1}v
T−1v(其中
v
v
v 是列向量)。现在你可能会问,在新基下描述这个变换的矩阵是什么。答案是,这个矩阵是
T
−
1
A
T
T^{-1}AT
T−1AT。
Well, so far, so good. What I memorized back then is that under basis change a matrix transforms as
T
−
1
A
T
T^{-1}AT
T−1AT.
到目前为止,一切都还顺利。我当时记住的是,在基变换下,矩阵按照
T
−
1
A
T
T^{-1}AT
T−1AT 的方式变换。
But then, we learned about quadratic forms. Those are calculated using a matrix
A
A
A as
u
T
A
v
u^T A v
uTAv. Still, no problem, until we learned about how to do basis changes. Now, suddenly the matrix did not transform as
T
−
1
A
T
T^{-1}AT
T−1AT, but rather as
T
T
A
T
T^T A T
TTAT. Which confused me like hell: how could one and the same object transform differently when used in different contexts?
但后来,我们学习了二次型。二次型是用矩阵
A
A
A 按照
u
T
A
v
u^T A v
uTAv 来计算的。这仍然没有问题,直到我们学习了如何进行基变换。这时,突然发现这个矩阵不再按照
T
−
1
A
T
T^{-1}AT
T−1AT 的方式变换,而是按照
T
T
A
T
T^T A T
TTAT 的方式变换。这让我非常困惑:同一个对象在不同情境下使用时,怎么会有不同的变换方式呢?
Well, the solution is: because we are actually talking about different objects! In the first case, we are talking about a tensor that takes vectors to vectors. In the second case, we are talking about a tensor that takes two vectors into a scalar, or equivalently, which takes a vector to a covector.
答案是:因为我们实际上在谈论不同的对象!在第一种情况下,我们谈论的是一个将向量映射到向量的张量。在第二种情况下,我们谈论的是一个将两个向量映射到一个标量的张量,或者等价地说,是一个将向量映射到余向量的张量。
Now both tensors have
n
2
n^2
n2 components, and therefore it is possible to write those components in a
n
×
n
n \times n
n×n matrix. And since all operations are either linear or bilinear, the normal matrix-matrix and matrix-vector products together with transposition can be used to write the operations of the tensor. Only when looking at basis transformations, you see that both are, indeed, not the same, and the course did us (well, at least me) a disservice by not telling us that we are really looking at two different objects, and not just at two different uses of the same object, the matrix.
现在,这两种张量都有
n
2
n^2
n2 个分量,因此可以将这些分量写成一个
n
×
n
n \times n
n×n 的矩阵。而且由于所有运算要么是线性的,要么是双线性的,所以可以用常规的矩阵乘法、矩阵-向量乘法以及转置来表示张量的运算。只有在考察基变换时,你才会发现它们确实不是同一个东西,而这门课没有告诉我们其实我们看到的是两个不同的对象,而不仅仅是同一个对象(矩阵)的两种不同用法,这对我们(至少对我)是一种误导。
Indeed, speaking of a rank-2 tensor is not really accurate. The rank of a tensor has to be given by two numbers. The vector to vector mapping is given by a rank-(1,1) tensor, while the quadratic form is given by a rank-(0,2) tensor. There’s also the type (2,0) which also corresponds to a matrix, but which maps two covectors to a number, and which again transforms differently.
实际上,说“秩为 2 的张量”并不十分准确。张量的秩必须由两个数来表示。将向量映射到向量的是 (1,1) 型张量,而二次型由 (0,2) 型张量表示。还有 (2,0) 型张量,它也对应一个矩阵,但它将两个余向量映射到一个数,并且其变换方式也不同。
The bottom line of this is:
归根结底:
-
The components of a rank-2 tensor can be written in a matrix.
秩为 2 的张量的分量可以写成一个矩阵。 -
The tensor is not that matrix, because different types of tensors can correspond to the same matrix.
张量不是那个矩阵,因为不同类型的张量可以对应同一个矩阵。 -
The differences between those tensor types are uncovered by the basis transformations (hence the physicist’s definition: “A tensor is what transforms like a tensor”).
这些张量类型之间的差异在基变换中会显现出来(因此物理学家的定义是:“张量是按照张量的方式变换的东西”)。
Of course, another difference between matrices and tensors is that matrices are by definition two-index objects, while tensors can have any rank.
当然,矩阵和张量之间的另一个区别是,矩阵本质上是双指标对象,而张量可以有任意的秩。
This is a great answer, because it reveals the question to be wrong. In fact, a matrix is not even a matrix, much less a tensor.
这是一个很棒的回答,因为它揭示了这个问题本身是错误的。事实上,矩阵甚至都不是矩阵,更不用说是张量了。
I’m happy with the first sentence in your comment @RyanReich but utterly confused by: “a matrix is not even a matrix”. Could you elaborate or point towards another source to explain this (unless I’ve taken it out of context?) Thanks.
@RyanReich,我对你评论中的第一句话表示认同,但完全被“矩阵甚至都不是矩阵”这句话搞糊涂了。你能详细解释一下吗,或者指出另一个可以解释这一点的来源(除非我断章取义了)?谢谢。
@AJP It’s been a while, but I believe what I meant by that was that a matrix (array of numbers) is different from a matrix (linear transformation = (1,1) tensor). The same array of numbers can represent several different basis-independent objects when a particular basis is chosen for them.
@AJP 过了一段时间了,但我认为我的意思是,(数值数组形式的)矩阵与(作为线性变换的 = (1,1) 型张量的)矩阵是不同的。当为它们选择特定的基时,同一个数值数组可以表示几个不同的与基无关的对象。
Proof basis change rule for quadratic form
q
=
[
x
y
z
]
[
A
]
[
x
y
z
]
q = [x\ y\ z][A]\begin{bmatrix}x\\y\\z\end{bmatrix}
q=[x y z][A]
xyz
证明二次型
q
=
[
x
y
z
]
[
A
]
[
x
y
z
]
q = [x\ y\ z][A]\begin{bmatrix}x\\y\\z\end{bmatrix}
q=[x y z][A]
xyz
的基变换规则
with
P
P
P being the change of basis matrix between
x
,
y
,
z
x,y,z
x,y,z and
u
,
v
,
w
u,v,w
u,v,w.
其中
P
P
P 是
x
,
y
,
z
x,y,z
x,y,z 和
u
,
v
,
w
u,v,w
u,v,w 之间的基变换矩阵。
q = [ x y z ] [ x y z ] = [ x y z ] ⊤ [ A ] [ x y z ] = ( P [ u v w ] ) ⊤ [ A ] P [ u v w ] = [ u v w ] P ⊤ [ A ] P [ u v w ] \begin{align*} q&=[x\ y\ z]\begin{bmatrix}x\\y\\z\end{bmatrix}\\ &=\begin{bmatrix}x\\y\\z\end{bmatrix}^\top[A]\begin{bmatrix}x\\y\\z\end{bmatrix}\\ &=\left(P\begin{bmatrix}u\\v\\w\end{bmatrix}\right)^\top[A]P\begin{bmatrix}u\\v\\w\end{bmatrix}\\ &=[u\ v\ w]P^\top[A]P\begin{bmatrix}u\\v\\w\end{bmatrix} \end{align*} q=[x y z] xyz = xyz ⊤[A] xyz = P uvw ⊤[A]P uvw =[u v w]P⊤[A]P uvw
Indeed there are some “confusions” some people do when talking about tensors. This happens mainly on Physics where tensors are usually described as “objects with components which transform in the right way”. To really understand this matter, let’s first remember that those objects belong to the realm of linear algebra. Even though they are used a lot in many branches of mathematics the area of mathematics devoted to the systematic study of those objects is really linear algebra.
的确,有些人在谈论张量时会存在一些“困惑”。这主要发生在物理学中,在物理学里,张量通常被描述为“其分量按照特定方式变换的对象”。要真正理解这个问题,让我们首先记住这些对象属于线性代数的范畴。尽管它们在许多数学分支中被大量使用,但专门系统研究这些对象的数学领域实际上是线性代数。
So let’s start with two vector spaces
V
,
W
V, W
V,W over some field of scalars
F
F
F. Now, let
T
:
V
→
W
T: V \to W
T:V→W be a linear transformation. I’ll assume that you know that we can associate a matrix with
T
T
T. Now, you might say: so linear transformations and matrices are all the same! And if you say that, you’ll be wrong. The point is: one can associate a matrix with
T
T
T only when one fix some basis of
V
V
V and some basis of
W
W
W. In that case we will get
T
T
T represented on those bases, but if we don’t introduce those,
T
T
T will be
T
T
T and matrices will be matrices (rectangular arrays of numbers, or whatever definition you like).
那么让我们从某个标量域
F
F
F 上的两个向量空间
V
,
W
V, W
V,W 开始。现在,设
T
:
V
→
W
T: V \to W
T:V→W 是一个线性变换。我假设你知道我们可以将一个矩阵与
T
T
T 相关联。这时,你可能会说:所以线性变换和矩阵是一回事!如果你这么说,那你就错了。关键在于:只有当我们固定
V
V
V 的某个基和
W
W
W 的某个基时,才能将一个矩阵与
T
T
T 相关联。在这种情况下,我们会得到
T
T
T 在这些基下的表示,但如果不引入这些基,
T
T
T 就是
T
T
T,而矩阵就是矩阵(矩形的数值数组,或任何你喜欢的定义)。
Now, the construction of tensors is much more elaborate than just saying: “take a set of numbers, label by components, let they transform in the correct way, you get a tensor”. In truth, this “definition” is a consequence of the actual definition. Indeed the actual definition of a tensor is meant to introduce what we call “Universal Property”.
现在,张量的构造远比“取一组数,用分量标记,让它们按照正确的方式变换,你就得到了一个张量”这种说法要复杂得多。事实上,这个“定义”是实际定义的一个推论。的确,张量的实际定义是为了引入我们所说的“泛性质”。
The point is that if we have a collection of
p
p
p vector spaces
V
i
V_i
Vi and another vector space
W
W
W we can form functions of several variables
f
:
V
1
×
⋯
×
V
p
→
W
f: V_1 \times \cdots \times V_p \to W
f:V1×⋯×Vp→W. A function like this will be called multilinear if it’s linear in each argument with the others held fixed. Now, since we know how to study linear transformations we ask ourselves: is there a construction of a vector space
S
S
S and one universal multilinear map
T
:
V
1
×
⋯
×
V
p
→
S
T: V_1 \times \cdots \times V_p \to S
T:V1×⋯×Vp→S such that
f
=
g
∘
T
f = g \circ T
f=g∘T for some
g
:
S
→
W
g: S \to W
g:S→W linear and such that this holds for all
f
f
f? If that’s always possible we’ll reduce the study of multilinear maps to the study of linear maps.
关键在于,如果我们有
p
p
p 个向量空间
V
i
V_i
Vi 的集合和另一个向量空间
W
W
W,我们可以构造多变量函数
f
:
V
1
×
⋯
×
V
p
→
W
f: V_1 \times \cdots \times V_p \to W
f:V1×⋯×Vp→W。如果这样的函数在每个自变量上都是线性的(其他自变量固定),那么它就被称为多线性函数。现在,由于我们知道如何研究线性变换,我们会问自己:是否存在一个向量空间
S
S
S 和一个“泛”多线性映射
T
:
V
1
×
⋯
×
V
p
→
S
T: V_1 \times \cdots \times V_p \to S
T:V1×⋯×Vp→S,使得对于某个线性映射
g
:
S
→
W
g: S \to W
g:S→W,有
f
=
g
∘
T
f = g \circ T
f=g∘T,并且这对所有
f
f
f 都成立?如果这总是可能的,我们就可以将多线性映射的研究简化为线性映射的研究。
The happy part of the story is that this is always possible, the construction is well defined and
S
S
S is denoted
V
1
⊗
⋯
⊗
V
p
V_1 \otimes \cdots \otimes V_p
V1⊗⋯⊗Vp and is called the tensor product of the vector spaces and the map
T
T
T is the tensor product of the vectors. An element
t
∈
S
t \in S
t∈S is called a tensor. Now it’s possible to prove that if
V
i
V_i
Vi has dimension
n
i
n_i
ni then the following relation holds:
这个故事中令人愉快的部分是,这总是可能的,这个构造是定义良好的,并且
S
S
S 记为
V
1
⊗
⋯
⊗
V
p
V_1 \otimes \cdots \otimes V_p
V1⊗⋯⊗Vp,称为向量空间的张量积,而映射
T
T
T 是向量的张量积。
S
S
S 中的元素
t
∈
S
t \in S
t∈S 被称为张量。现在可以证明,如果
V
i
V_i
Vi 的维数为
n
i
n_i
ni,则有以下关系成立:
dim ( V 1 ⊗ ⋯ ⊗ V p ) = ∏ i = 1 p n i \dim(V_1 \otimes \cdots \otimes V_p) = \prod_{i=1}^p n_i dim(V1⊗⋯⊗Vp)=i=1∏pni
This means that
S
S
S has a basis with
∏
i
=
1
p
n
i
\prod_{i=1}^p n_i
∏i=1pni elements. In that case, as we know from basic linear algebra, we can associate with every
t
∈
S
t \in S
t∈S its components in some basis. Now, those components are what people usually call “the tensor”. Indeed, when you see in Physics people saying: “consider the tensor
T
α
β
T_{\alpha\beta}
Tαβ” what they are really saying is “consider the tensor
T
T
T whose components in some basis understood by context are
T
α
β
T_{\alpha\beta}
Tαβ”.
这意味着
S
S
S 有一个包含
∏
i
=
1
p
n
i
\prod_{i=1}^p n_i
∏i=1pni 个元素的基。在这种情况下,正如我们从基本线性代数中所知,我们可以将每个
t
∈
S
t \in S
t∈S 与其在某个基下的分量相关联。现在,这些分量就是人们通常所说的“张量”。事实上,当你在物理学中看到人们说“考虑张量
T
α
β
T_{\alpha\beta}
Tαβ”时,他们真正的意思是“考虑在上下文所理解的某个基下,分量为
T
α
β
T_{\alpha\beta}
Tαβ 的张量
T
T
T”。
So if we consider two vector spaces
V
1
V_1
V1 and
V
2
V_2
V2 with dimensions respectivly
n
n
n and
m
m
m, by the result I’ve stated
dim
(
V
1
⊗
V
2
)
=
n
m
\dim(V_1 \otimes V_2) = nm
dim(V1⊗V2)=nm, so for every tensor
t
∈
V
1
⊗
V
2
t \in V_1 \otimes V_2
t∈V1⊗V2 one can associate a set of
n
m
nm
nm scalars (the components of
t
t
t), and we are obviously allowed to plug those values into a matrix
M
(
t
)
M(t)
M(t) and so there’s a correspondence of tensors of rank 2 with matrices.
因此,如果我们考虑两个向量空间
V
1
V_1
V1 和
V
2
V_2
V2,它们的维数分别为
n
n
n 和
m
m
m,根据我所陈述的结果,
dim
(
V
1
⊗
V
2
)
=
n
m
\dim(V_1 \otimes V_2) = nm
dim(V1⊗V2)=nm,所以对于每个张量
t
∈
V
1
⊗
V
2
t \in V_1 \otimes V_2
t∈V1⊗V2,我们可以将其与一组
n
m
nm
nm 个标量(
t
t
t 的分量)相关联,显然我们可以将这些值放入一个矩阵
M
(
t
)
M(t)
M(t) 中,因此秩为 2 的张量与矩阵之间存在对应关系。
However, exactly as in the linear transformation case this correspondence is only possible when we have selected bases on the vector spaces we are dealing with. Finally, with every tensor it is possible to associate also a multilinear map. So tensors can be understood in their fully abstract and algebraic way as elements of the tensor product of vector spaces, and can also be understood as multilinear maps (this is better for intuition) and we can associate matrices to those.
然而,正如在线性变换的情况下一样,这种对应关系只有在我们为所处理的向量空间选择了基之后才有可能。最后,每个张量还可以与一个多线性映射相关联。因此,张量可以以完全抽象和代数的方式理解为向量空间张量积的元素,也可以理解为多线性映射(这更符合直觉),并且我们可以将矩阵与这些张量相关联。
So after all this hassle with linear algebra, the short answer to your question is: matrices are matrices, tensors of rank 2 are tensors of rank 2, however there’s a correspondence between them whenever you fix a basis on the space of tensors.
因此,在经历了这么多线性代数的麻烦之后,对你的问题的简短回答是:矩阵就是矩阵,秩为 2 的张量就是秩为 2 的张量,然而,当你在张量空间上固定一个基时,它们之间存在对应关系。
My suggestion is that you read Kostrikin’s “Linear Algebra and Geometry” chapter 4 on multilinear algebra. This book is hard, but it’s good to really get the ideas. Also, you can see about tensors (constructions in terms of multilinear maps) in good books of multivariable Analysis like “Calculus on Manifolds” by Michael Spivak or “Analysis on Manifolds” by James Munkres.
我的建议是你阅读柯斯特利金的《线性代数与几何》中关于多线性代数的第 4 章。这本书很难,但对于真正理解这些概念很有帮助。此外,你可以在好的多变量分析书籍中了解张量(从多线性映射的角度构建),例如迈克尔·斯皮瓦克的《流形上的微积分》或詹姆斯·芒克雷斯的《流形分析》。
I must be missing something, but can’t you just set
S
=
W
,
g
=
Id
W
S = W, g = \text{Id}_W
S=W,g=IdW?
我一定是漏掉了什么,但你不能直接设
S
=
W
,
g
=
Id
W
S = W, g = \text{Id}_W
S=W,g=IdW 吗?
The point is that we want a space
S
S
S constructed from the vector spaces
V
i
V_i
Vi such that we can use it for all
W
W
W. In other words, given just
V
i
V_i
Vi we can build the pair
(
S
,
g
)
(S, g)
(S,g) and use once and for all for any
W
W
W and
f
f
f. That is why it is calles universal property.
关键在于,我们想要一个由向量空间
V
i
V_i
Vi 构造的空间
S
S
S,使得我们可以将它用于所有的
W
W
W。换句话说,仅给定
V
i
V_i
Vi,我们就可以构建出对
(
S
,
g
)
(S, g)
(S,g),并一劳永逸地用于任何
W
W
W 和
f
f
f。这就是为什么它被称为泛性质。
As a place-holder answer waiting perhaps for clarification by the questioner’s (and others’) reaction: given that your context has a matrix be a table of values (which can be entirely reasonable)…
作为一个临时答案,或许等待提问者(和其他人)的反馈来澄清:假设在你的语境中,矩阵是一个数值表格(这完全是合理的)……
In that context, a “vector” is a list of values, a “matrix” is a table (or list of lists), the next item would be a list of tables (equivalently, a table of lists, or list of lists of lists), then a table of tables (equivalently, a list of tables of lists, or list of lists of tables…). And so on. All these are “tensors”.
在这种语境下,“向量”是一个数值列表,“矩阵”是一个表格(或列表的列表),接下来的是表格的列表(等价地,列表的表格,或列表的列表的列表),然后是表格的表格(等价地,列表的表格的列表,或列表的列表的表格……),依此类推。所有这些都是“张量”。
Unsurprisingly, there are many more sophisticated viewpoints that can be taken, but perhaps this bit of sloganeering is useful?
不出所料,可以有许多更复杂的观点,但或许这种简单的说法是有用的?
In addition to the answer of celtschk, this makes tensors make some sense to me (and their different ranks)
除了 celtschk 的回答 之外,这让我对张量(以及它们的不同秩)有了一些理解
So basically a tensor is an array of objects in programming. Tensor1 = array. Tensor2 = array of array. Tensor3 = array of array of array.
所以基本上,在编程中,张量是对象的数组。1 阶张量 = 数组。2 阶张量 = 数组的数组。3 阶张量 = 数组的数组的数组。
@Pacerier, yes, from a programming viewpoint that would be a reasonable starter-version of what a tensor is. But, as noted in my answer, in various mathematical contexts there is complication, due, in effect, to “collapsing” in the indexing scheme.
@Pacerier,是的,从编程的角度来看,这是对张量的一个合理的初步理解。但是,正如我在回答中提到的,在各种数学语境中,由于索引方案中的“压缩”,情况会变得复杂。
@paulgarrett Can we say objects with a rank of more than 2 are tensors? or a scalar is also a tensor?
@paulgarrett 我们可以说秩大于 2 的对象是张量吗?或者标量也是张量?
Yes, we can (if we insist) say that a scalar is a tensor of rank 0. And, yes, there are higher-rank tensors: sometimes that higher rank is visible in the number of subscripts and/or superscripts they carry. Such things arise in geometry (and, thereby, in general relativity).
是的,我们可以(如果我们坚持的话)说标量是秩为 0 的张量。而且,是的,存在更高秩的张量:有时这种更高的秩可以从它们所带的下标和/或上标的数量中看出。这类东西出现在几何学中(从而也出现在广义相对论中)。
Tensors are objects whose transformation laws make them geometrically meaningful. Yes, I am a physicist, and to me, that is what a tensor is: there is a general idea that tensors are objects merely described using components with respect to some basis, and as coordinates change (and thus the associated basis changes), the tensor’s components should transform accordingly. What those laws are follows, then, from the chain rule of multivariable calculus, nothing more.
张量是其变换规律使其具有几何意义的对象。是的,我是一名物理学家,对我来说,这就是张量的定义:普遍的观点是,张量只是用相对于某个基的分量来描述的对象,并且当坐标变化时(从而相关的基也变化时),张量的分量应该相应地变换。这些规律源于多变量微积分的链式法则,仅此而已。
What is a matrix? A representation of a linear map, also with respect to some basis. Thus, some tensors can be represented with matrices.
什么是矩阵?矩阵是线性映射的一种表示,也是相对于某个基的。因此,一些张量可以用矩阵来表示。
Why some? Well, contrary to what you may have heard, not all tensors are inherently linear maps. Yes, you can construct a linear map from any tensor, but that is not what the tensor is. From a vector, you can construct a linear map acting on a covector to produce a scalar; this is where the idea comes from, but it’s misleading. Consider a different kind of quantity, representing an oriented plane. We’ll call it a bivector: From a bivector, you can construct a linear map taking in a covector and returning a vector, or a linear map taking two covectors and returning a scalar.
为什么是“一些”?嗯,与你可能听到的相反,并非所有张量本质上都是线性映射。是的,你可以从任何张量构造一个线性映射,但这并不是张量本身。从一个向量,你可以构造一个作用于余向量以产生标量的线性映射;这就是这个想法的来源,但它具有误导性。考虑一种不同的量,它表示一个有向平面。我们称之为双向量:从双向量,你可以构造一个接收余向量并返回向量的线性映射,或者一个接收两个余向量并返回标量的线性映射。
That you can construct multiple maps from a bivector should indicate that the bivector is, in itself, neither of these maps but a more fundamental geometric object. Bivectors are represented using antisymmetric 2-index tesors, or antisymmetric matrices. In fact, you can form bivectors from two vectors. While you can make that fit with the mapping picture, it starts to feel incredibly arbitrary.
你可以从双向量构造多个映射,这表明双向量本身既不是这些映射中的任何一个,而是一个更基本的几何对象。双向量用反对称的 2 指标张量或反对称矩阵来表示。事实上,你可以从两个向量形成双向量。虽然你可以让它符合映射的图景,但这开始让人觉得非常随意。
Some tensors are inherently linear maps, however, and all such maps can be written in terms of some basis as a matrix. Even the Riemann tensor, which has
(
n
2
)
(
n
2
)
(n^2)(n^2)
(n2)(n2) by
(
n
2
)
(
n
2
)
(n^2)(n^2)
(n2)(n2) components, can be written this way, even though it’s usually considered a map of two vectors to two vectors, three vectors to one vector, four vectors to a scalar…I could go on.
然而,有些张量本质上是线性映射,并且所有这些映射都可以根据某个基写成矩阵形式。即使是黎曼张量,它有
(
n
2
)
(
n
2
)
×
(
n
2
)
(
n
2
)
(n^2)(n^2) \times (n^2)(n^2)
(n2)(n2)×(n2)(n2) 个分量,也可以这样写,尽管它通常被认为是将两个向量映射到两个向量、三个向量映射到一个向量、四个向量映射到一个标量……我可以继续列举下去。
But not all matrices represent information that is suitable for such geometric considerations.
但并非所有矩阵都代表适合这种几何考量的信息。
Your interpretation of bivectors as rank 2 antisymmetric tensors is very interesting. Where does it find its justification ? Could one construct something similar or analogous for “cobivectors”, outer products of 2 covectors, or 2-forms ? This could help provide interesting visualizations of 2-forms.
你将双向量解释为秩 2 的反对称张量,这非常有趣。这种解释的依据是什么?人们可以为“余双向量”、两个余向量的外积或 2 - 形式构造类似的东西吗?这可能有助于提供 2 - 形式的有趣可视化。
The shortest answer I can come up with is that a Tensor is described by a matrix (or rank 1 vector) but also the type of thing represented. Matrices have no such “type” associated with them. If you misapply linear algebra on inconsistently typed matrices the math yields mathematically valid garbage.
我能想到的最简短的答案是,张量由矩阵(或秩 1 向量)描述,但还包含所表示事物的类型。矩阵没有与之相关联的这种“类型”。如果你将线性代数错误地应用于类型不一致的矩阵,得到的结果在数学上是有效的,但毫无意义。
Intuitively you can’t transform apples into peach pie. But you can transform apples into apple pie. Matrices have no intrinsic type associated with them so a linear algebra recipe to do the peach pie transform will produce garbage from the apples matrix.
直观地说,你不能把苹果变成桃派。但你可以把苹果变成苹果派。矩阵没有内在的相关类型,所以一个用于制作桃派的线性代数方法,用在苹果矩阵上会产生毫无意义的结果。
A more mathematical example is that if you have a vector describing text terms in a document and a vector describing DNA codes, you cannot take the cosine of the normalized vectors (dot product) to see how “similar” they are. The dot product is mathematically valid but since they are from different types and represent different things the dot product is meaningless garbage. But if you do the same with 2 text term vectors you can make statements about how similar they are from the result, it is indeed not garbage.
一个更具数学性的例子是,如果你有一个描述文档中文本术语的向量和一个描述 DNA 编码的向量,你不能通过计算归一化向量的余弦(点积)来判断它们有多“相似”。点积在数学上是有效的,但由于它们来自不同的类型并代表不同的事物,这个点积是毫无意义的。但如果你对两个文本术语向量做同样的事情,你可以从结果中判断它们的相似程度,这确实是有意义的。
What I’m calling “type” is more rigorously defined but the above gets the gist I think.
我所说的“类型”有更严格的定义,但我认为上面的内容抓住了要点。
All matrices are not tensors, although all tensors of rank 2 are matrices.
并非所有矩阵都是张量,尽管所有秩为 2 的张量都是矩阵。
Example
示例
T = [ x − y x 2 − y 2 ] T = \begin{bmatrix}x & -y \\ x^2 & -y^2\end{bmatrix} T=[xx2−y−y2]
This matrix
T
T
T is not tensor rank 2. We test matrix
T
T
T to rotation matrix
这个矩阵
T
T
T 不是秩为 2 的张量。我们用旋转矩阵来测试矩阵
T
T
T
A = [ cos ( θ ) sin ( θ ) − sin ( θ ) cos ( θ ) ] A = \begin{bmatrix}\cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta)\end{bmatrix} A=[cos(θ)−sin(θ)sin(θ)cos(θ)]
Now, expand tensor equation rank 2, for example
现在,展开秩为 2 的张量方程,例如
T 11 ′ = Σ ( A 1 i ∗ A 1 j ∗ T i j ) (1) T'_{11} = \Sigma (A_{1i} * A_{1j} * T_{ij}) \quad \tag{1} T11′=Σ(A1i∗A1j∗Tij)(1)
Now, calculate
现在,计算
T 11 ′ = x ′ = x ∗ cos ( θ ) + y ∗ sin ( θ ) (2) T'_{11} = x' = x * \cos(\theta) + y * \sin(\theta) \quad \tag{2} T11′=x′=x∗cos(θ)+y∗sin(θ)(2)
You see (1) is unequal to (2), then we can conclude that the matrix
T
T
T isn’t a tensor of rank 2.
你可以看到(1)与(2)不相等,因此我们可以得出结论:矩阵
T
T
T 不是秩为 2 的张量。
Tensor must follow the conversion(transformation) rules, but matrices generally are not.
张量必须遵循变换规则,但矩阵通常不遵循。
Should you not sum over all indices in equation 2? So you would get
x
cos
2
−
y
(
cos
+
sin
)
+
x
2
(
cos
+
sin
)
−
y
2
sin
2
x \cos^2 - y (\cos + \sin) + x^2 (\cos + \sin) - y^2 \sin^2
xcos2−y(cos+sin)+x2(cos+sin)−y2sin2 (if I interpret your formula correctly, you sum over all
i
i
i and
j
j
j, right?)
你不应该在方程 2 中对所有指标求和吗?那么你会得到
x
cos
2
−
y
(
cos
+
sin
)
+
x
2
(
cos
+
sin
)
−
y
2
sin
2
x \cos^2 - y (\cos + \sin) + x^2 (\cos + \sin) - y^2 \sin^2
xcos2−y(cos+sin)+x2(cos+sin)−y2sin2(如果我对你的公式理解正确的话,你要对所有的
i
i
i 和
j
j
j 求和,对吗?)
Also, would that not just show that it is not a rank (2,0) tensor, but not that it is not a rank 2 tensor in general (like 1,1 or 0,2)?
此外,这难道不只是表明它不是(2,0)型张量,而不是表明它一般不是秩为 2 的张量(比如(1,1)型或(0,2)型)吗?
Why the sudden fascination with tensors?
为何人们突然对张量产生浓厚兴趣?
edited Jul 4, 2016 at 5:30
I’ve noticed lately that a lot of people are developing tensor equivalents of many methods (tensor factorization, tensor kernels, tensors for topic modeling, etc) I’m wondering, why is the world suddenly fascinated with tensors? Are there recent papers/ standard results that are particularly surprising, that brought about this? Is it computationally a lot cheaper than previously suspected?
我最近注意到,很多人正在开发许多方法的张量等价形式(张量分解、张量核、用于主题建模的张量等)。我在想,为什么世界突然对张量如此着迷?是否有最近的论文或标准结果特别令人惊讶,从而引发了这种现象?它在计算上是否比之前预想的便宜得多?
I’m not being glib, I sincerely am interested, and if there are any pointers to papers about this, I’d love to read them.
我并非随口一问,我是真心感兴趣,如果有相关论文的参考资料,我很乐意阅读。
It seems like the only retaining feature that “big data tensors” share with the usual mathematical definition is that they are multidimensional arrays. So I’d say that big data tensors are a marketable way of saying “multidimensional array,” because I highly doubt that machine learning people will care about either the symmetries or transformation laws that the usual tensors of mathematics and physics enjoy, especially their usefulness in forming coordinate free equations.
“大数据张量”与通常的数学定义仅有的共同特征似乎是它们都是多维数组。因此,我认为“大数据张量”是“多维数组”的一种市场化说法,因为我非常怀疑机器学习领域的人会关心数学和物理学中常见张量所具有的对称性或变换规律,尤其是它们在形成无坐标方程方面的作用。
—— Alex R.
Commented Feb 23, 2016 at 19:00
@AlexR. without invariance to transformations there are no tensors
@亚历克斯·R. 没有变换不变性,就不存在张量。
—— Aksakal
Commented Feb 23, 2016 at 21:43
Putting on my mathematical hat I can say that there is no intrinsic symmetry to a mathematical tensor. Further, they are another way to say ‘multidimensional array’. One could vote for using the word tensor over using the phrase multidimensional array simply on grounds of simplicity. In particular if
V
V
V is a
n
n
n-dimensional vector space, one can identify
V
⊗
V
V \otimes V
V⊗V with
n
n
n by
n
n
n matrices.
从数学的角度来说,数学张量没有内在的对称性。此外,它们是“多维数组”的另一种说法。仅仅出于简洁性,人们可能会选择使用“张量”一词而非“多维数组”这一短语。特别是如果
V
V
V 是一个
n
n
n 维向量空间,我们可以将
V
⊗
V
V \otimes V
V⊗V 等同于
n
×
n
n \times n
n×n 矩阵。
—— meh
Commented Feb 24, 2016 at 14:47
@aginensky If a tensor were nothing more than a multidimensional array, then why do the definitions of tensors found in math textbooks sound so complicated? From Wikipedia: “The numbers in the multidimensional array are known as the scalar components of the tensor… Just as the components of a vector change when we change the basis of the vector space, the components of a tensor also change under such a transformation. Each tensor comes equipped with a transformation law that details how the components of the tensor respond to a change of basis.” In math, a tensor is not just an array.
@aginensky 如果张量只不过是多维数组,那么为什么数学教科书中的张量定义听起来如此复杂?来自维基百科:“多维数组中的数被称为张量的标量分量……正如当我们改变向量空间的基时向量的分量会发生变化一样,张量的分量在这种变换下也会发生变化。每个张量都配备有一个变换规律,详细说明张量的分量如何响应基的变化。” 在数学中,张量不仅仅是一个数组。
—— littleO
Commented Feb 25, 2016 at 0:55
Just some general thoughts on this discussion: I think that, as with vectors and matrices, the actual application often becomes a much-simplified instantiation of much richer theory. I am reading this paper in more depth: Tensor Decompositions and Applications and one thing that is really impressing me is that the “representational” tools for matrices (eigenvalue and singular value decompositions) have interesting generalizations in higher orders. I’m sure there are many more beautiful properties as well, beyond just a nice container for more indices.
Tensor Decompositions and Applications
Authors: Tamara G. Kolda and Brett W. BaderAuthors Info & Affiliations
https://doi.org/10.1137/07070111X
关于这场讨论的一些普遍想法:我认为,与向量和矩阵一样,实际应用往往是更丰富理论的一种高度简化的实例。我正在更深入地阅读这篇论文:张量分解和应用,让我印象深刻的一点是,矩阵的“表示性”工具(特征值分解和奇异值分解)在更高阶数上有有趣的推广。我确信除了作为容纳更多索引的良好容器之外,它们还有许多更优美的性质。
—— Y. S.
Commented Feb 25, 2016 at 15:40
Answers
This is not an answer to your question, but an extended comment on the issue that has been raised here in comments by different people, namely: are machine learning “tensors” the same thing as tensors in mathematics?
这并非对你问题的回答,而是对不同人在评论中提出的问题的延伸评论,即:机器学习中的“张量”与数学中的张量是同一事物吗?
Now, according to the Cichoki 2014, Era of Big Data Processing: A New Approach via Tensor Networks and Tensor Decompositions, and Cichoki et al. 2014, Tensor Decompositions for Signal Processing Applications,
根据 Cichoki 2014 年的论文《大数据处理时代:通过张量网络和张量分解的新方法》(arXiv:1403.2048)以及Cichoki等人2014年的论文《用于信号处理应用的张量分解》(arXiv:1403.4462):
A higher-order tensor can be interpreted as a multiway array, […]
高阶张量可以解释为多路数组,[…]
A tensor can be thought of as a multi-index numerical array, […]
张量可以被视为多索引数值数组,[…]
Tensors (i.e., multi-way arrays) […]
张量(即多路数组)[…]
So in machine learning / data processing a tensor appears to be simply defined as a multidimensional numerical array. An example of such a 3D tensor would be 1000 video frames of 640×480 size. A usual
n
×
p
n \times p
n×p data matrix is an example of a 2D tensor according to this definition.
因此,在机器学习/数据处理中,“张量”似乎被简单定义为多维数值数组。这种三维张量的一个例子是1000个640×480大小的视频帧。根据这个定义,通常的
n
×
p
n \times p
n×p 数据矩阵是二维张量的一个例子。
This is not how tensors are defined in mathematics and physics!
这并非数学和物理学中张量的定义方式!
A tensor can be defined as a multidimensional array obeying certain transformation laws under the change of coordinates (see Wikipedia or the first sentence in MathWorld article). A better but equivalent definition (see Wikipedia) says that a tensor on vector space
V
V
V is an element of
V
⊗
…
⊗
V
∗
V \otimes \ldots \otimes V^*
V⊗…⊗V∗. Note that this means that, when represented as multidimensional arrays, tensors are of size
p
×
p
p \times p
p×p or
p
×
p
×
p
p \times p \times p
p×p×p etc., where
p
p
p is the dimensionality of
V
V
V.
张量可以定义为在坐标变换下遵循特定变换规律的多维数组(参见维基百科或 MathWorld文章的第一句)。一个更好但等价的定义(参见维基百科)指出,向量空间
V
V
V 上的张量是
V
⊗
…
⊗
V
∗
V \otimes \ldots \otimes V^*
V⊗…⊗V∗ 中的一个元素。请注意,这意味着当表示为多维数组时,张量的大小为
p
×
p
p \times p
p×p 或
p
×
p
×
p
p \times p \times p
p×p×p 等,其中
p
p
p 是
V
V
V 的维数。
All tensors well-known in physics are like that: inertia tensor in mechanics is
3
×
3
3 \times 3
3×3, electromagnetic tensor in special relativity is
4
×
4
4 \times 4
4×4, Riemann curvature tensor in general relativity is
4
×
4
×
4
×
4
4 \times 4 \times 4 \times 4
4×4×4×4. Curvature and electromagnetic tensors are actually tensor fields, which are sections of tensor bundles (see [e.g. here](https://books.google.pt/books?id=2ydvda4F1VEC&lpg=PA163&ots=-ZYnjDcEpE&dq=tensor bundle&pg=PA163#v=onepage&q=tensor bundle&f=false) but it gets technical), but all of that is defined over a vector space
V
V
V.
物理学中所有著名的张量都是如此:力学中的惯性张量是
3
×
3
3 \times 3
3×3 的,狭义相对论中的电磁张量是
4
×
4
4 \times 4
4×4 的,广义相对论中的黎曼曲率张量是
4
×
4
×
4
×
4
4 \times 4 \times 4 \times 4
4×4×4×4 的。曲率张量和电磁张量实际上是张量场,它们是张量丛的截面(例如参见[这里](https://books.google.pt/books?id=2ydvda4F1VEC&lpg=PA163&ots=-ZYnjDcEpE&dq=tensor bundle&pg=PA163#v=onepage&q=tensor bundle&f=false),但内容较为专业),但所有这些都是在向量空间
V
V
V 上定义的。
Of course one can construct a tensor product
V
⊗
W
V \otimes W
V⊗W of an
p
p
p-dimensional
V
V
V and
q
q
q-dimensional
W
W
W but its elements are usually not called “tensors”, as stated e.g. here on Wikipedia:
当然,我们可以构造
p
p
p 维空间
V
V
V 和
q
q
q 维空间
W
W
W 的张量积
V
⊗
W
V \otimes W
V⊗W,但正如维基百科中所述,其元素通常不被称为“张量”:
In principle, one could define a “tensor” simply to be an element of any tensor product. However, the mathematics literature usually reserves the term tensor for an element of a tensor product of a single vector space V V V and its dual, as above.
原则上,人们可以简单地将“张量”定义为任何张量积中的元素。然而,数学文献通常将“张量”一词保留用于单个向量空间 V V V 与其对偶空间的张量积中的元素,如上所述。
One example of a real tensor in statistics would be a covariance matrix. It is
p
×
p
p \times p
p×p and transforms in a particular way when the coordinate system in the
p
p
p-dimensional feature space
V
V
V is changed. It is a tensor. But a
n
×
p
n \times p
n×p data matrix
X
X
X is not.
统计学中一个真正的张量例子是协方差矩阵。它是
p
×
p
p \times p
p×p 的,当
p
p
p 维特征空间
V
V
V 中的坐标系发生变化时,它会以特定方式变换。它是一个张量。但
n
×
p
n \times p
n×p 的数据矩阵
X
X
X 不是。
But can we at least think of
X
X
X as an element of tensor product
W
⊗
V
W \otimes V
W⊗V, where
W
W
W is
n
n
n-dimensional and
V
V
V is
p
p
p-dimensional? For concreteness, let rows in
X
X
X correspond to people (subjects) and columns to some measurements (features). A change of coordinates in
V
V
V corresponds to linear transformation of features, and this is done in statistics all the time (think of PCA). But a change of coordinates in
W
W
W does not seem to correspond to anything meaningful (and I urge anybody who has a counter-example to let me know in the comments). So it does not seem that there is anything gained by considering
X
X
X as an element of
W
⊗
V
W \otimes V
W⊗V.
但我们至少能将
X
X
X 视为张量积
W
⊗
V
W \otimes V
W⊗V 中的一个元素吗?其中
W
W
W 是
n
n
n 维的,
V
V
V 是
p
p
p 维的。具体来说,设
X
X
X 中的行对应于人员(对象),列对应于某些测量值(特征)。
V
V
V 中的坐标变换对应于特征的线性变换,这在统计学中很常见(例如主成分分析)。但
W
W
W 中的坐标变换似乎不对应任何有意义的东西(我恳请任何有反例的人在评论中告诉我)。因此,将
X
X
X 视为
W
⊗
V
W \otimes V
W⊗V 中的元素似乎没有任何意义。
And indeed, the common notation is to write
X
∈
R
n
×
p
X \in \mathbb{R}^{n \times p}
X∈Rn×p, where
R
n
×
p
\mathbb{R}^{n \times p}
Rn×p is a set of all
n
×
p
n \times p
n×p matrices (which, by the way, are defined as rectangular arrays of numbers, without any assumed transformation properties).
事实上,常见的记法是
X
∈
R
n
×
p
X \in \mathbb{R}^{n \times p}
X∈Rn×p,其中
R
n
×
p
\mathbb{R}^{n \times p}
Rn×p 是所有
n
×
p
n \times p
n×p 矩阵的集合(顺便说一下,矩阵被定义为 数字的矩形数组,没有任何假定的变换性质)。
My conclusion is: (a) machine learning tensors are not math/physics tensors, and (b) it is mostly not useful to see them as elements of tensor products either.
我的结论是:(a)机器学习中的张量不是数学/物理学中的张量;(b)将它们视为张量积的元素通常也没有意义。
Instead, they are multidimensional generalizations of matrices. Unfortunately, there is no established mathematical term for that, so it seems that this new meaning of “tensor” is now here to stay.
相反,它们是矩阵的多维推广。不幸的是,对此没有既定的数学术语,因此“张量”的这种新含义似乎将保留下来。
edited Sep 3, 2016 at 23:55
amoeba
I am a pure mathematician, and this is a very good answer. In particular, the example of a covariance matrix is an excellent way to understand the “transformation properties” or “symmetries” that seemed to cause confusion above. If you change coordinates on your
p
p
p-dimensional feature space, the covariance matrix transforms in a particular and possibly surprising way; if you did the more naive transformation on your covariances you would end up with incorrect results.
我是一名纯数学家,这是一个非常好的回答。特别是协方差矩阵的例子,是理解上述似乎引起混淆的“变换性质”或“对称性”的绝佳方式。如果你在
p
p
p 维特征空间中改变坐标,协方差矩阵会以一种特定且可能令人惊讶的方式变换;如果你对协方差进行更简单的变换,最终会得到错误的结果。
—— Tom Church
Commented Feb 25, 2016 at 4:08
Thanks, @Tom, I appreciate that you registered on CrossValidated to leave this comment. It has been a long time since I was studying differential geometry so I am happy if somebody confirms what I wrote. It is a pity that there is no established term in mathematics for “multidimensional matrices”; it seems that “tensor” is going to stick in machine learning community as a term for that. How do you think one should rather call it though? The best thing that comes to my mind is
n
n
n-matrices (e.g. 3-matrix to refer to a video object), somewhat analogously to
n
n
n-categories.
谢谢@汤姆,感谢你注册CrossValidated来留下这条评论。我学习微分几何已经很久了,所以如果有人能证实我所写的内容,我会很高兴。遗憾的是,数学中没有“多维矩阵”的既定术语;似乎“张量”一词将在机器学习社区中作为其术语保留下来。不过,你认为应该称它为什么呢?我能想到的最好的是
n
n
n-矩阵(例如,用3-矩阵指代视频对象),这在某种程度上类似于
n
n
n-范畴。
—— amoeba
Commented Feb 25, 2016 at 10:25
@amoeba, in programming the multidemensional matrices are usually called arrays, but some languages such as MATLAB would call them matrices. For instance, in FORTRAN the arrays can have more than 2 dimensions. In languages like C/C++/Java the arrays are one dimensional, but you can have arrays of arrays, making them work like multidimensional arrays too. MATLAB supports 3 or more dimensional arrays in the syntax.
@阿米巴,在编程中,多维矩阵通常被称为“数组”(arrays),但有些语言如MATLAB会称它们为“矩阵”(matrices)。例如,在FORTRAN中,数组可以有超过2个维度。在C/C++/Java等语言中,数组是一维的,但你可以有数组的数组,使它们也能像多维数组一样工作。MATLAB在语法上支持3维或更高维的数组。
—— Aksakal
Commented Feb 25, 2016 at 15:17
That is very interesting. I hope you will emphasize that point. But please take some care not to confuse a set with a vector space it determines, because the distinction is important in statistics. In particular (to pick up one of your examples), although a linear combination of people is meaningless, a linear combination of real-valued functions on a set of people is both meaningful and important. It’s the key to solving linear regression, for instance.
这非常有趣。我希望你能强调这一点。但请注意不要将一个集合与其所确定的向量空间混淆,因为这种区别在统计学中很重要。特别是(以你的一个例子为例),虽然人的线性组合是没有意义的,但一组人上的实值函数的线性组合既有意义又很重要。例如,这是解决线性回归的关键。
—— whuber♦
Commented Jul 5, 2016 at 13:56
Per T. Kolda, B, Bada,“Tensor Decompositions and Applications” SIAM Review 2009, epubs.siam.org/doi/pdf/10.1137/07070111X 'A tensor is a multidimensional array. More formally, an N-way or Nth-order tensor is an element of the tensor product of N vector spaces, each of which has its own coordinate system. This notion of tensors is not to be confused with tensors in physics and engineering (such as stress tensors), which are generally referred to as tensor fields in mathematics "
根据T. Kolda、B. Bada在《张量分解及其应用》(《SIAM评论》2009年)(epubs.siam.org/doi/pdf/10.1137/07070111X)中的说法:“张量是一个多维数组。更正式地说,N阶张量是N个向量空间的张量积中的一个元素,每个向量空间都有自己的坐标系。这种张量的概念不应与物理学和工程学中的张量(如应力张量)相混淆,后者在数学中通常被称为张量场。”
—— Mark L. Stone
Commented Sep 3, 2016 at 20:31
Tensors often offer more natural representations of data, e.g., consider video, which consists of obviously correlated images over time. You can turn this into a matrix, but it’s just not natural or intuitive (what does a factorization of some matrix-representation of video mean?).
张量通常能更自然地表示数据,例如,考虑视频,它由随时间变化的、明显相关的图像组成。你可以将其转换为矩阵,但这并不自然或直观(视频的某种矩阵表示的分解意味着什么?)。
Tensors are trending for several reasons:
张量之所以流行,有几个原因:
-
our understanding of multilinear algebra is improving rapidly, specifically in various types of factorizations, which in turn helps us to identify new potential applications (e.g., multiway component analysis)
我们对多线性代数的理解正在迅速提高,特别是在各种类型的分解方面,这反过来帮助我们发现新的潜在应用(例如,多路成分分析) -
software tools are emerging (e.g., Tensorlab) and are being welcomed
软件工具正在涌现(例如,Tensorlab)并受到欢迎 -
Big Data applications can often be solved using tensors, for example recommender systems, and Big Data itself is hot
大数据应用通常可以使用张量来解决,例如推荐系统,而大数据本身很热门 -
increases in computational power, as some tensor operations can be hefty (this is also one of the major reasons why deep learning is so popular now)
计算能力的提升,因为一些张量运算可能很庞大(这也是深度学习现在如此流行的主要原因之一)
edited Feb 23, 2016 at 9:55
Marc Claesen
On the computational power part: I think the most important is that linear algebra can be very fast on GPUs, and lately they have gotten bigger and faster memories, that is the biggest limitation when processing large data.
关于计算能力部分:我认为最重要的是,线性代数运算在GPU上可以非常快,而且最近GPU的内存变得更大、速度更快,而内存是处理大数据时最大的限制。
—— Davidmh
Commented Feb 23, 2016 at 12:17
Marc Claesen’s answer is a good one. David Dunson, Distinguished Professor of Statistics at Duke, has been one of the key exponents of tensor-based approaches to modeling as in this presentation, Bayesian Tensor Regression. icerm.brown.edu/materials/Slides/sp-f12-w1/…
马克·克拉森的回答很好。杜克大学统计学杰出教授戴维·邓森一直是基于张量的建模方法的主要倡导者,如本次演讲《贝叶斯张量回归》中所述。
—— user78229
Commented Feb 23, 2016 at 14:36
As mentioned by David, Tensor algorithms often lend themselves well to parallelism, which hardware (such as GPU accelerators) are increasingly getting better at.
正如戴维所提到的,张量算法通常非常适合并行处理,而硬件(如GPU加速器)在这方面的能力正日益增强。
—— Thomas Russell
Commented Feb 23, 2016 at 15:15
I assumed that the better memory/CPU capabilities were playing a part, but the very recent burst of attention was interesting; I think it must be because of a lot of recent surprising successes with recommender systems, and perhaps also kernels for SVMs, etc. Thanks for the links! great places to start learning about this stuff…
我认为更好的内存/CPU能力起到了一定作用,但最近突然受到关注很有趣;我想这一定是因为最近在推荐系统方面取得了很多令人惊讶的成功,或许还有支持向量机的核函数等。感谢这些链接!是学习这些东西的好起点……
—— Y. S.
Commented Feb 24, 2016 at 7:20
If you store a video as a multidimensional array, I don’t see how this multidimensional array would have any of the invariance properties a tensor is supposed to have. It doesn’t seem like the word “tensor” is appropriate in this example.
如果你将视频存储为多维数组,我看不出这个多维数组会具有张量应有的任何不变性。在这个例子中,“张量”一词似乎并不合适。
—— littleO
Commented Feb 24, 2016 at 8:45
I think your question should be matched with an answer that is equally free flowing and open minded as the question itself. So, here they are my two analogies.
我认为你的问题应该得到一个与问题本身一样自由流畅、思想开放的回答。因此,我有两个类比。
First, unless you’re a pure mathematician, you were probably taught univariate probabilities and statistics first. For instance, most likely your first OLS example was probably on a model like this:
首先,除非你是纯数学家,否则你可能首先学习的是单变量概率和统计。例如,你接触的第一个普通最小二乘法…(OLS)例子很可能是这样的模型:
y i = a + b x i + e i y_i = a + b x_i + e_i yi=a+bxi+ei
Most likely, you went through deriving the estimates through actually minimizing the sum of least squares:
很可能,你通过实际最小化残差平方和来推导估计值:
T S S = ∑ i ( y i − a ˉ − b ˉ x i ) 2 TSS = \sum_i (y_i - \bar{a} - \bar{b} x_i)^2 TSS=i∑(yi−aˉ−bˉxi)2
Then you write the FOCs for parameters and get the solution:
然后你写出参数的一阶条件…(FOC)并得到解:
∂ T T S ∂ a ˉ = 0 \frac{\partial TTS}{\partial \bar{a}} = 0 ∂aˉ∂TTS=0
Then later you’re told that there’s an easier way of doing this with vector (matrix) notation:
之后,你会被告知用向量(矩阵)符号有更简单的方法:
y = X b + e y = X b + e y=Xb+e
and the TTS becomes:
此时TTS变为:
T T S = ( y − X b ˉ ) ′ ( y − X b ˉ ) TTS = (y - X \bar{b})' (y - X \bar{b}) TTS=(y−Xbˉ)′(y−Xbˉ)
The FOCs are:
一阶条件为:
2 X ′ ( y − X b ˉ ) = 0 2 X' (y - X \bar{b}) = 0 2X′(y−Xbˉ)=0
And the solution is
解为:
b ˉ = ( X ′ X ) − 1 X ′ y \bar{b} = (X' X)^{-1} X' y bˉ=(X′X)−1X′y
If you’re good at linear algebra, you’ll stick to the second approach once you’ve learned it, because it’s actually easier than writing down all the sums in the first approach, especially once you get into multivariate statistics.
如果你擅长线性代数,一旦学会第二种方法,你就会坚持使用它,因为它实际上比第一种方法中写下所有求和式更容易,尤其是当你进入多元统计领域时。
Hence my analogy is that moving to tensors from matrices is similar to moving from vectors to matrices: if you know tensors some things will look easier this way.
因此,我的类比是,从矩阵过渡到张量类似于从向量过渡到矩阵:如果你了解张量,有些事情用这种方式会显得更简单。
Second, where do the tensors come from? I’m not sure about the whole history of this thing, but I learned them in theoretical mechanics. Certainly, we had a course on tensors, but I didn’t understand what was the deal with all these fancy ways to swap indices in that math course. It all started to make sense in the context of studying tension forces.
其次,张量来自哪里?我不确定它的整个历史,但我是在理论力学中学习张量的。当然,我们有一门张量课程,但在那门数学课上,我不明白所有这些花哨的索引交换方式有什么意义。在研究张力的背景下,这一切才开始变得有意义。
So, in physics they also start with a simple example of pressure defined as force per unit area, hence:
因此,在物理学中,他们也从一个简单的例子开始,即压力定义为单位面积上的力,因此:
F = p ⋅ d S F = p \cdot dS F=p⋅dS
This means you can calculate the force vector
F
F
F by multiplying the pressure
p
p
p (scalar) by the unit of area
d
S
dS
dS (normal vector). That is when we have only one infinite plane surface. In this case there’s just one perpendicular force. A large balloon would be good example.
这意味着你可以通过将压力
p
p
p(标量)乘以面积单位
d
S
dS
dS(法向量)来计算力向量
F
F
F。这是当我们只有一个无限大平面时的情况。在这种情况下,只有一个垂直力。一个大气球就是一个很好的例子。
However, if you’re studying tension inside materials, you are dealing with all possible directions and surfaces. In this case you have forces on any given surface pulling or pushing in all directions, not only perpendicular ones. Some surfaces are torn apart by tangential forces “sideways” etc. So, your equation becomes:
然而,如果你在研究材料内部的张力,你会涉及所有可能的方向和表面。在这种情况下,任何给定表面上的力都会在所有方向上拉或推,而不仅仅是垂直方向。有些表面会被“侧向”的切向力撕裂等。因此,你的方程变为:
F = P ⋅ d S F = P \cdot dS F=P⋅dS
The force is still a vector
F
F
F and the surface area is still represented by its normal vector
d
S
dS
dS, but
P
P
P is a tensor now, not a scalar.
力仍然是向量
F
F
F,表面积仍然由其法向量
d
S
dS
dS 表示,但
P
P
P 现在是一个张量,而不是标量。
Ok, a scalar and a vector are also tensors
好吧,标量和向量也是张量
Another place where tensors show up naturally is co-variance or correlation matrices. Just think of this: how to transform one correlation matrix
C
0
C_0
C0 to another one
C
1
C_1
C1? You realize we can’t just do it this way:
张量自然出现的另一个地方是协方差矩阵或相关矩阵。想想看:如何将一个相关矩阵
C
0
C_0
C0 变换为另一个相关矩阵
C
1
C_1
C1?你会意识到我们不能这样做:
C θ ( i , j ) = C 0 ( i , j ) + θ ( C 1 ( i , j ) − C 0 ( i , j ) ) , C_\theta (i,j) = C_0 (i,j) + \theta (C_1 (i,j) - C_0 (i,j)), Cθ(i,j)=C0(i,j)+θ(C1(i,j)−C0(i,j)),
where
θ
∈
[
0
,
1
]
\theta \in [0,1]
θ∈[0,1] because we need to keep all
C
θ
C_\theta
Cθ positive semi-definite.
其中
θ
∈
[
0
,
1
]
\theta \in [0,1]
θ∈[0,1],因为我们需要保持所有
C
θ
C_\theta
Cθ 都是半正定的。
So, we’d have to find the path
δ
C
θ
\delta C_\theta
δCθ such that
C
1
=
C
0
+
∫
θ
δ
C
θ
C_1 = C_0 + \int_\theta \delta C_\theta
C1=C0+∫θδCθ, where
δ
C
θ
\delta C_\theta
δCθ is a small disturbance to a matrix. There are many different paths, and we could search for the shortest ones. That’s how we get into Riemannian geometry, manifolds, and… tensors.
因此,我们必须找到路径
δ
C
θ
\delta C_\theta
δCθ,使得
C
1
=
C
0
+
∫
θ
δ
C
θ
C_1 = C_0 + \int_\theta \delta C_\theta
C1=C0+∫θδCθ,其中
δ
C
θ
\delta C_\theta
δCθ 是对矩阵的一个小扰动。有许多不同的路径,我们可以寻找最短的路径。这就是我们进入黎曼几何、流形以及……张量的原因。
UPDATE: what’s tensor, anyway?
更新:到底什么是张量?
@amoeba and others got into a lively discussion of the meaning of tensor and whether it’s the same as an array. So, I thought an example is in order.
@阿米巴和其他人就张量的含义以及它是否与数组相同展开了热烈的讨论。因此,我认为有必要举一个例子。
Say, we go to a bazaar to buy groceries, and there are two merchant dudes,
d
1
d_1
d1 and
d
2
d_2
d2. We noticed that if we pay
x
1
x_1
x1 dollars to
d
1
d_1
d1 and
x
2
x_2
x2 dollars to
d
2
d_2
d2 then
d
1
d_1
d1 sells us
y
1
=
2
x
1
−
x
2
y_1 = 2 x_1 - x_2
y1=2x1−x2 pounds of apples, and
d
2
d_2
d2 sells us
y
2
=
−
0.5
x
1
+
2
x
2
y_2 = -0.5 x_1 + 2 x_2
y2=−0.5x1+2x2 pounds of oranges. For instance, if we pay both 1 dollar, i.e.
x
1
=
x
2
=
1
x_1 = x_2 = 1
x1=x2=1 then we must get 1 pound of apples and 1.5 of oranges.
假设我们去集市买杂货,有两个商人,
d
1
d_1
d1 和
d
2
d_2
d2。我们“注意到”,如果我们付给
d
1
d_1
d1
x
1
x_1
x1 美元,付给
d
2
d_2
d2
x
2
x_2
x2 美元,那么
d
1
d_1
d1 会卖给我们
y
1
=
2
x
1
−
x
2
y_1 = 2 x_1 - x_2
y1=2x1−x2 磅苹果,
d
2
d_2
d2 会卖给我们
y
2
=
−
0.5
x
1
+
2
x
2
y_2 = -0.5 x_1 + 2 x_2
y2=−0.5x1+2x2 磅橙子。例如,如果我们各付1美元,即
x
1
=
x
2
=
1
x_1 = x_2 = 1
x1=x2=1,那么我们会得到1磅苹果和1.5磅橙子。
We can express this relation in the form of a matrix
P
P
P:
我们可以用矩阵
P
P
P 的形式表示这种关系:
2 -1
-0.5 2
Then the merchants produce this much apples and oranges if we pay them
x
x
x dollars:
如果我们付给商人
x
x
x 美元,他们会提供这么多苹果和橙子:
y = P x y = P x y=Px
This works exactly like a matrix by vector multiplication.
这完全像矩阵与向量的乘法。
Now, let’s say instead of buying the goods from these merchants separately, we declare that there are two spending bundles we utilize. We either pay both 0.71 dollars, or we pay
d
1
d_1
d1 0.71 dollars and demand 0.71 dollars from
d
2
d_2
d2 back. Like in the initial case, we go to a bazaar and spend
z
1
z_1
z1 on the bundle one and
z
2
z_2
z2 on the bundle 2.
现在,假设我们不是分别从这些商人那里购买商品,而是声明我们使用两种消费组合。我们要么各付0.71美元,要么付给
d
1
d_1
d1 0.71美元,并要求
d
2
d_2
d2 返还0.71美元。和最初的情况一样,我们去集市,在组合1上花费
z
1
z_1
z1,在组合2上花费
z
2
z_2
z2。
So, let’s look at an example where we spend just
z
1
=
2
z_1 = 2
z1=2 on bundle 1. In this case, the first merchant gets
x
1
=
1
x_1 = 1
x1=1 dollars, and the second merchant gets the same
x
2
=
1
x_2 = 1
x2=1. Hence, we must get the same amounts of produce like in the example above, aren’t we?
那么,让我们看一个例子,我们只在组合1上花费
z
1
=
2
z_1 = 2
z1=2。在这种情况下,第一个商人得到
x
1
=
1
x_1 = 1
x1=1 美元,第二个商人也得到
x
2
=
1
x_2 = 1
x2=1 美元。因此,我们必须得到与上面例子中相同数量的农产品,不是吗?
Maybe, maybe not. You noticed that
P
P
P matrix is not diagonal. This indicates that for some reason how much one merchant charges for his produce depends also on how much we paid the other merchant. They must get an idea of how much pay them, maybe through rumors? In this case, if we start buying in bundles they’ll know for sure how much we pay each of them, because we declare our bundles to the bazaar. In this case, how do we know that the
P
P
P matrix should stay the same?
可能是,也可能不是。你注意到
P
P
P 矩阵不是对角矩阵。这表明,由于某种原因,一个商人对其商品的收费还取决于我们付给另一个商人的钱数。他们一定知道我们付了多少,也许是通过谣言?在这种情况下,如果我们开始按组合购买,他们肯定会知道我们付给每个人多少钱,因为我们向集市声明了我们的组合。在这种情况下,我们怎么知道
P
P
P 矩阵应该保持不变呢?
Maybe with full information of our payments on the market the pricing formulas would change too! This will change our matrix
P
P
P, and there’s no way to say how exactly.
也许有了我们在市场上付款的完整信息,定价公式也会改变!这将改变我们的矩阵
P
P
P,而且无法确切说明会如何改变。
This is where we enter tensors. Essentially, with tensors we say that the calculations do not change when we start trading in bundles instead of directly with each merchant. That’s the constraint, that will impose transformation rules on
P
P
P, which we’ll call a tensor.
这就是我们进入张量领域的地方。本质上,对于张量,我们说当我们开始按组合交易而不是直接与每个商人交易时,计算结果不会改变。这是一种约束,它将对
P
P
P 施加变换规则,我们将
P
P
P 称为张量。
Particularly we may notice that we have an orthonormal basis
d
ˉ
1
,
d
ˉ
2
\bar{d}_1, \bar{d}_2
dˉ1,dˉ2, where
d
i
d_i
di means a payment of 1 dollar to a merchant
i
i
i and nothing to the other. We may also notice that the bundles also form an orthonormal basis
d
ˉ
1
′
,
d
ˉ
2
′
\bar{d}'_1, \bar{d}'_2
dˉ1′,dˉ2′, which is also a simple rotation of the first basis by 45 degrees counterclockwise. It’s also a PC decomposition of the first basis. hence, we are saying that switching to the bundles is simple a change of coordinates, and it should not change the calculations. Note, that this is an outside constraint that we imposed on the model. It didn’t come from pure math properties of matrices.
特别是,我们可能会注意到我们有一个标准正交基
d
ˉ
1
,
d
ˉ
2
\bar{d}_1, \bar{d}_2
dˉ1,dˉ2,其中
d
i
d_i
di 表示付给商人
i
i
i 1美元,而不付给另一个人。我们可能还会注意到,这些组合也形成了一个标准正交基
d
ˉ
1
′
,
d
ˉ
2
′
\bar{d}'_1, \bar{d}'_2
dˉ1′,dˉ2′,它也是第一个基逆时针旋转45度的简单旋转。它也是第一个基的主成分分解。因此,我们说切换到组合只是坐标的改变,不应改变计算结果。请注意,这是我们施加给模型的外部约束,它并非来自矩阵的纯数学性质。
Now, our shopping can be expressed as a vector
x
=
x
1
d
ˉ
1
+
x
2
d
ˉ
2
x = x_1 \bar{d}_1 + x_2 \bar{d}_2
x=x1dˉ1+x2dˉ2. The vectors are tensors too, BTW. The tensor is interesting: it can be represented as
现在,我们的购物可以表示为向量
x
=
x
1
d
ˉ
1
+
x
2
d
ˉ
2
x = x_1 \bar{d}_1 + x_2 \bar{d}_2
x=x1dˉ1+x2dˉ2。顺便说一下,向量也是张量。这个张量很有趣:它可以表示为
P = ∑ i j p i j d ˉ i d ˉ j P = \sum_{i j} p_{i j} \bar{d}_i \bar{d}_j P=ij∑pijdˉidˉj
, and the groceries as
y
=
y
1
d
ˉ
1
+
y
2
d
ˉ
2
y = y_1 \bar{d}_1 + y_2 \bar{d}_2
y=y1dˉ1+y2dˉ2. With groceries
y
i
y_i
yi means pound of produce from the merchant
i
i
i, not the dollars paid.
而杂货表示为
y
=
y
1
d
ˉ
1
+
y
2
d
ˉ
2
y = y_1 \bar{d}_1 + y_2 \bar{d}_2
y=y1dˉ1+y2dˉ2。对于杂货,
y
i
y_i
yi 表示从商人
i
i
i 那里得到的农产品磅数,而不是支付的美元数。
Now, when we changed the coordinates to bundles the tensor equation stays the same:
现在,当我们将坐标改为组合时,张量方程保持不变:
y = P z y = P z y=Pz
That’s nice, but the payment vectors are now in the different basis:
这很好,但支付向量现在处于不同的基下:
z = z 1 d ˉ 1 ′ + z 2 d ˉ 2 ′ z = z_1 \bar{d}'_1 + z_2 \bar{d}'_2 z=z1dˉ1′+z2dˉ2′
, while we may keep the produce vectors in the old basis
y
=
y
1
d
ˉ
1
+
y
2
d
ˉ
2
y = y_1 \bar{d}_1 + y_2 \bar{d}_2
y=y1dˉ1+y2dˉ2. The tensor changes too:
而我们可以将农产品向量保持在旧基下
y
=
y
1
d
ˉ
1
+
y
2
d
ˉ
2
y = y_1 \bar{d}_1 + y_2 \bar{d}_2
y=y1dˉ1+y2dˉ2。张量也会变化:
P = ∑ i j p i j ′ d ˉ i ′ d ˉ j ′ P = \sum_{i j} p'_{i j} \bar{d}'_i \bar{d}'_j P=ij∑pij′dˉi′dˉj′
. It’s easy to derive how the tensor must be transformed, it’s going to be
P
A
P A
PA, where the rotation matrix is defined as
d
ˉ
′
=
A
d
ˉ
\bar{d}' = A \bar{d}
dˉ′=Adˉ. In our case it’s the coefficient of the bundle.
很容易推导出张量必须如何变换,它将是
P
A
P A
PA,其中旋转矩阵定义为
d
ˉ
′
=
A
d
ˉ
\bar{d}' = A \bar{d}
dˉ′=Adˉ。在我们的例子中,它是组合的系数。
We can work out the formulas for tensor transformation, and they’ll yield the same result as in the examples with
x
1
=
x
2
=
1
x_1 = x_2 = 1
x1=x2=1 and
z
1
=
0.71
,
z
2
=
0
z_1 = 0.71, z_2 = 0
z1=0.71,z2=0.
我们可以推导出张量变换的公式,它们将得到与
x
1
=
x
2
=
1
x_1 = x_2 = 1
x1=x2=1 和
z
1
=
0.71
,
z
2
=
0
z_1 = 0.71, z_2 = 0
z1=0.71,z2=0 的例子相同的结果。
edited Dec 13, 2019 at 7:02
I got confused around here: So, let's look at an example where we spend just z1=1.42 on bundle 1. In this case, the first merchant gets x1=1 dollars, and the second merchant gets the same x2=1. Earlier you say that first bundle is that we pay both 0.71 dollars. So spending 1.42 on the first bundle should get 0.71 each and not 1, no?
我在这里有点困惑:“那么,让我们看一个例子,我们只在组合1上花费z1=1.42。在这种情况下,第一个商人得到x1=1美元,第二个商人也得到x2=1美元。” 你之前说第一个组合是我们“各付0.71美元”。所以在第一个组合上花费1.42应该各得到0.71,而不是1,不是吗?
—— amoeba
Commented Feb 25, 2016 at 10:32
@ameba, the idea’s that a bundle 1 is
d
ˉ
1
/
2
+
d
ˉ
2
/
2
\bar{d}_1 / \sqrt{2} + \bar{d}_2 / \sqrt{2}
dˉ1/2+dˉ2/2, so with
2
\sqrt{2}
2 bundle 1 you get
d
ˉ
1
+
d
ˉ
2
\bar{d}_1 + \bar{d}_2
dˉ1+dˉ2, i.e. 1$ each
@阿米巴,这个想法是组合1是
d
ˉ
1
/
2
+
d
ˉ
2
/
2
\bar{d}_1 / \sqrt{2} + \bar{d}_2 / \sqrt{2}
dˉ1/2+dˉ2/2,所以用
2
\sqrt{2}
2 个组合1,你会得到
d
ˉ
1
+
d
ˉ
2
\bar{d}_1 + \bar{d}_2
dˉ1+dˉ2,即各1美元。
—— Aksakal
Commented Feb 25, 2016 at 14:44
@Aksakal, I know this discussion is quite old, but I don’t get that either (although I was really trying to). Where does that idea that a bundle 1 is
d
ˉ
1
/
2
+
d
ˉ
2
/
2
\bar{d}_1 / \sqrt{2} + \bar{d}_2 / \sqrt{2}
dˉ1/2+dˉ2/2 come from? Could you elaborate? How is that when you pay 1.42 for the bundle both merchants get 1?
@阿克萨卡尔,我知道这个讨论已经很久了,但我也不明白(尽管我真的很努力去理解)。组合1是
d
ˉ
1
/
2
+
d
ˉ
2
/
2
\bar{d}_1 / \sqrt{2} + \bar{d}_2 / \sqrt{2}
dˉ1/2+dˉ2/2 这个想法来自哪里?你能详细说明一下吗?为什么当你为这个组合支付1.42时,两个商人各得到1美元?
—— Matek
Commented Sep 14, 2016 at 8:16
- @Aksakal This is great, thanks! I think you have a typo on the very last line, where you say x1 = x2 = 1 (correct) and z1 = 0.71, z2 = 0. Presuming I understood everything correctly, z1 should be 1.42 (or 1.41, which is slightly closer to 2^0.5).
@阿克萨卡尔,这很棒,谢谢!我认为你在最后一行有一个笔误,你说x1 = x2 = 1(正确),z1 = 0.71,z2 = 0。假设我理解正确的话,z1应该是1.42(或者1.41,更接近2^0.5)。
—— Mike Williamson
Commented Aug 3, 2017 at 2:14
- @Aksakal from “Now, our shopping can be expressed as a vector…” your post is a bit unclear. Would you mind explaining it a bit more detail please? What’s the
P
P
P notation you’re using? Could this simply be explained in terms of change of basis? With your notation, it seems like
A
A
A would be the matrix for change of basis from
d
′
d'
d′ to
d
d
d, correct? I.e. to get the “transformation” w.r.t bundle basis, we compose the transformation w.r.t. starting basis together with the change of basis matrix, correct?
@阿克萨卡尔,从“现在,我们的购物可以表示为一个向量……”开始,你的帖子有点不清楚。你介意更详细地解释一下吗?你使用的 P P P 符号是什么意思?这能简单地用基的变换来解释吗?根据你的符号,似乎 A A A 是从 d ′ d' d′ 到 d d d 的基变换矩阵,对吗?也就是说,为了得到相对于组合基的“变换”,我们将相对于初始基的变换与基变换矩阵组合起来,对吗?
—— Jake1234
Commented Sep 26, 2020 at 21:12
As someone who studies and builds neural networks and has repeatedly asked this question, I’ve come to the conclusion that we borrow useful aspects of tensor notation simply because they make derivation a lot easier and keep our gradients in their native shapes. The tensor chain rule is one of the most elegant derivation tools I have ever seen. Further tensor notations encourage computationally efficient simplifications that are simply nightmarish to find when using common extended versions of vector calculus.
作为研究和构建神经网络并反复问这个问题的人,我得出的结论是,我们借鉴张量符号的有用方面,仅仅是因为它们使推导变得容易得多,并使我们的梯度保持其原生形状。张量链式法则是我见过的最优雅的推导工具之一。此外,张量符号有助于实现计算上高效的简化,而这些简化在使用常见的向量微积分扩展版本时是难以实现的。
In Vector/Matrix calculus for instance there are 4 types of matrix products (Hadamard, Kronecker, Ordinary, and Elementwise) but in tensor calculus there is only one type of multiplication yet it covers all matrix multiplications and more. If you want to be generous, interpret tensor to mean multi-dimensional array that we intend to use tensor based calculus to find derivatives for, not that the objects we are manipulating are tensors*.
例如,在向量/矩阵微积分中,有4种矩阵乘积(哈达玛积、克罗内克积、普通积和元素积),但在张量微积分*中,只有一种乘法,却涵盖了所有矩阵乘法甚至更多。如果你想宽容一点,可以将张量解释为我们打算使用基于张量的微积分来求导的多维数组,而不是说我们正在操作的对象是张量。
In all honesty we probably call our multi-dimensional arrays tensors because most machine learning experts don’t care that much about adhering to the definitions of high level math or physics. The reality is we are just borrowing well developed Einstein Summation Conventions and Calculi which are typically used when describing tensors and don’t want to say Einstein summation convention based calculus over and over again. Maybe one day we might develop a new set of notations and conventions that steal only what they need from tensor calculus specifically for analyzing neural networks, but as a young field that takes time.
老实说,我们可能将多维数组称为张量,是因为大多数机器学习专家并不太在意是否遵循高等数学或物理学的定义。事实上,我们只是在借用发展完善的爱因斯坦求和约定和微积分,这些通常在描述张量时使用,而不想一遍又一遍地说基于爱因斯坦求和约定的微积分。也许有一天,我们会开发出一套新的符号和约定,专门从张量微积分中提取分析神经网络所需的部分,但作为一个年轻的领域,这需要时间。
edited Jul 5, 2017 at 22:10
– gung - Reinstate Monica
Commented Jul 4, 2017 at 1:17
Now I actually agree with most of the content of the other answers. But I’m going to play Devil’s advocate on one point. Again, it will be free flowing, so apologies…
现在我实际上同意其他回答的大部分内容。但在一点上我要唱反调。再次说明,这将是自由发挥的,所以先致歉……
Google announced a program called Tensor Flow for deep learning. This made me wonder what was ‘tensor’ about deep learning, as I couldn’t make the connection to the definitions I’d seen.
谷歌宣布了一个名为Tensor Flow(张量流)的深度学习程序。这让我想知道深度学习中的“张量”是什么,因为我无法将其与我所看到的定义联系起来。
Deep learning models are all about transformation of elements from one space to another. E.g. if we consider two layers of some network you might write co-ordinate
i
i
i of a transformed variable
y
y
y as a nonlinear function of the previous layer, using the fancy summation notation:
深度学习模型全是关于元素从一个空间到另一个空间的变换。例如,如果我们考虑某个网络的两层,你可以使用复杂的求和符号,将变换变量
y
y
y 的坐标
i
i
i 写成前一层的非线性函数:
y i = σ ( β j i x j ) y_i = \sigma (\beta_{j i} x_j) yi=σ(βjixj)
Now the idea is to chain together a bunch of such transformations in order to arrive at a useful representation of the original co-ordinates. So, for example, after the last transformation of an image a simple logistic regression will produce excellent classification accuracy; whereas on the raw image it would definitely not.
现在的想法是将一系列这样的变换串联起来,以得到原始坐标的有用表示。例如,在对图像进行最后一次变换后,简单的逻辑回归会产生出色的分类精度;而在原始图像上则肯定不会。
Now, the thing that seems to have been lost from sight is the invariance properties sought in a proper tensor. Particularly when the dimensions of transformed variables may be different from layer to layer. [E.g. some of the stuff I’ve seen on tensors makes no sense for non square Jacobians - I may be lacking some methods]
现在,似乎被忽略的是真正张量所追求的不变性。特别是当变换变量的维度可能在层与层之间不同时。(例如,我所看到的一些关于张量的内容对于非平方雅可比矩阵来说是没有意义的——我可能缺乏一些方法)
What has been retained is the notion of transformations of variables, and that certain representations of a vector may be more useful than others for particular tasks. Analogy being whether it makes more sense to tackle a problem in Cartesian or polar co-ordinates.
保留下来的是变量变换的概念,以及向量的某些表示对于特定任务可能比其他表示更有用。可以类比为在笛卡尔坐标还是极坐标下解决问题更有意义。
EDIT in response to @Aksakal:
编辑以回应@阿克萨卡尔:
The vector can’t be perfectly preserved because of the changes in the numbers of coordinates. However, in some sense at least the useful information may be preserved under transformation. For example with PCA we may drop a co-ordinate, so we can’t invert the transformation but the dimensionality reduction may be useful nonetheless. If all the successive transformations were invertible, you could map back from the penultimate layer to input space. As it is, I’ve only seen probabilistic models which enable that (RBMs) by sampling.
由于坐标数量的变化,向量无法被完美保留。然而,在某种意义上,至少有用的信息在变换下可能被保留。例如,在主成分分析中,我们可能会丢弃一个坐标,因此我们无法反转变换,但降维可能仍然有用。如果所有连续的变换都是可逆的,你可以从倒数第二层映射回输入空间。事实上,我只见过通过采样实现这一点的概率模型(受限玻尔兹曼机)。
edited Feb 25, 2016 at 22:34
conjectures
In the context of neural networks I had always assumed tensors were acting just as multidimensional arrays. Can you elaborate on how the invariance properties are aiding classification/representation?
在神经网络的背景下,我一直认为张量只是作为多维数组发挥作用。你能详细说明一下不变性如何帮助分类/表示吗?
—— Y. S.
Commented Feb 25, 2016 at 16:02
-
Maybe I wasn’t clear above, but it seems to me - if the interpretation is correct - the goal of invariant properties has been dropped. What seems to have been kept is the idea of variable transformations.
也许我上面说得不清楚,但在我看来——如果这种解释是正确的——不变性的目标已经被放弃了。似乎保留下来的是变量变换的思想。—— conjectures
Commented Feb 25, 2016 at 20:02 -
@conjectures, if you have a vector r ˉ \bar{r} rˉ in cartesian coordinates, then convert it to polar coordinates, the vector stays the same, i.e. it still point from the same point in the same direction. Are you saying that in machine learning the coordinate transformation changes the initial vector?
@猜想,如果你在笛卡尔坐标中有一个向量 r ˉ \bar{r} rˉ,然后将其转换为极坐标,这个向量保持不变,即它仍然从同一点指向同一方向。你是说在机器学习中,坐标变换会改变初始向量吗?—— Aksakal
Commented Feb 25, 2016 at 20:18 -
but isn’t that a property of the transformation more than the tensor? At least with linear and element-wise type transformations, which seem more popular in neural nets, they are equally present with vectors and matrices; what are the added benefits of the tensors?
但这不更是变换的性质而非张量的性质吗?至少对于线性和元素级的变换(在神经网络中似乎更流行),它们在向量和矩阵中同样存在;张量的额外好处是什么?—— Y. S.
Commented Feb 26, 2016 at 9:47
@conjectures, PCA is just a rotation and projection. It’s like rotating N-dimensional space to PC basis, then projecting to sub-space. Tensors are used in similar situations in physics, e.g. when looking at forces on the surfaces inside bodies etc.
@猜想,主成分分析只是一种旋转和投影。这就像将N维空间旋转到主成分基,然后投影到子空间。张量在物理学中的类似情况下使用,例如研究物体内部表面上的力等。
—— Aksakal
Commented Feb 26, 2016 at 12:32
Here is a lightly edited (for context) excerpt from Non-Negative Tensor Factorization with Applications to Statistics and Computer Vision, A. Shashua and T. Hazan_ which gets to the heart of why at least some people are fascinated with tensors.
以下是《非负张量分解及其在统计学和计算机视觉中的应用》(A. Shashua和T. Hazan著)…中的一段(为上下文略作编辑),它道出了至少一部分人对张量着迷的核心原因。
- Any n-dimensional problem can be represented in two dimensional form by concatenating dimensions. Thus for example, the problem of finding a non-negative low rank decomposition of a set of images is a 3-NTF (Non-negative Tensor Factorization), with the images forming the slices of a 3D cube, but can also be represented as an NMF (Non-negative Matrix Factorization) problem by vectorizing the images (images forming columns of a matrix).
任何n维问题都可以通过连接维度以二维形式表示。例如,寻找一组图像的非负低秩分解的问题是一个三维非负张量分解(3-NTF)问题,图像形成三维立方体的切片,但也可以通过将图像向量化(图像形成矩阵的列)表示为非负矩阵分解(NMF)问题。
There are two reasons why a matrix representation of a collection of images would not be appropriate:
图像集合的矩阵表示之所以不合适,有两个原因:
Spatial redundancy (pixels, not necessarily neighboring, having similar values) is lost in the vectorization thus we would expect a less efficient factorization, and
空间冗余(不一定相邻的、具有相似值的像素)在向量化过程中丢失,因此我们预计分解效率会较低;
- An NMF decomposition is not unique therefore even if there exists a generative model (of local parts) the NMF would not necessarily move in that direction, which has been verified empirically by Chu, M., Diele, F., Plemmons, R., & Ragni, S. “Optimality, computation and interpretation of nonnegative matrix factorizations” SIAM Journal on Matrix Analysis, 2004. For example, invariant parts on the image set would tend to form ghosts in all the factors and contaminate the sparsity effect. An NTF is almost always unique thus we would expect the NTF scheme to move towards the generative model, and specifically not be influenced by invariant parts.
非负矩阵分解不具有唯一性,因此即使存在(局部部分的)生成模型,非负矩阵分解也不一定会朝着该方向进行,这一点已由Chu, M.、Diele, F.、Plemmons, R.和Ragni, S.在《非负矩阵分解的最优性、计算和解释》(《SIAM矩阵分析期刊》,2004年)中通过实证验证。例如,图像集中的不变部分往往会在所有因子中形成虚影,并破坏稀疏性效果。而非负张量分解几乎总是唯一的,因此我们预计非负张量分解方案会朝着生成模型的方向进行,特别是不受不变部分的影响。
answered Sep 3, 2016 at 14:52
Mark L. Stone
Qualitatively, what is the difference between a matrix and a tensor?
从定性角度看,矩阵和张量的区别是什么?
edited Sep 21, 2015 at 13:00 rubik
asked Sep 21, 2015 at 1:49 Life_student
Qualitatively (or mathematically “light”), could someone describe the difference between a matrix and a tensor? I have only seen them used in the context of an undergraduate, upper level classical mechanics course, and within that context, I never understood the need to distinguish between matrices and tensors. They seemed like identical mathematical entities to me.
从定性角度(或说 “浅层次” 的数学角度),有人能描述一下矩阵和张量的区别吗?我只在本科高年级的经典力学课程中见过它们的应用,在那个语境下,我始终不明白为什么要区分矩阵和张量。在我看来,它们似乎是完全相同的数学实体。
Just as an aside, my math background is roughly the one of a typical undergraduate physics major (minus the linear algebra).
顺便说一下,我的数学背景大概相当于典型的本科物理专业学生(除了线性代数知识稍欠缺)。
edited Sep 21, 2015 at 13:00 rubik
asked Sep 21, 2015 at 1:49 Life_student
Answers
Coordinate-wise, one could say that a matrix is a “square” of numbers, while a tensor is an n-dimensional block of numbers. But this is horrible, not insightful and even a bit wrong, since those coordinates must “change in appropriate ways” (this is part of why this is horrible).
从坐标角度来说,可以认为矩阵是一个 “方形” 的数字集合,而张量是一个 n 维的数字块。但这种说法很糟糕、毫无洞见,甚至有点错误,因为这些坐标必须 “以恰当的方式变化”(这也是这种说法糟糕的部分原因)。
It may be best to think as follows: given a vector space V V V, a matrix can be seen in an adequate way as a bilinear map V ∗ × V → R V^* \times V \to \mathbb{R} V∗×V→R (since you asked for it, I’ll not enter into details. Here, V ∗ V^* V∗ is the dual of V V V). A tensor can be interpreted as a multilinear map V ∗ × ⋯ × V ∗ × V × ⋯ × V → R V^* \times \dots \times V^* \times V \times \dots \times V \to \mathbb{R} V∗×⋯×V∗×V×⋯×V→R (not necessarily the same quantity of V ∗ V^* V∗'s and V V V’s).
或许更好的理解方式是:给定一个向量空间 V V V,矩阵可以被恰当地视为一个双线性映射 V ∗ × V → R V^* \times V \to \mathbb{R} V∗×V→R(既然你问到了,我就不展开细节了。这里的 V ∗ V^* V∗ 是 V V V 的对偶空间)。而张量可以被解释为一个多线性映射 V ∗ × ⋯ × V ∗ × V × ⋯ × V → R V^* \times \dots \times V^* \times V \times \dots \times V \to \mathbb{R} V∗×⋯×V∗×V×⋯×V→R( V ∗ V^* V∗ 和 V V V 的数量不一定相同)。
Hence, a matrix is a kind of tensor. But tensors are more general.
因此,矩阵是张量的一种。但张量更为通用。
answered Sep 21, 2015 at 2:16 Aloizio Macedo♦
instead of horrible adjective, use a little more complex one : P
与其用 “糟糕” 这个词,不如用稍微复杂一点的表述嘛 : P
– janmarqz Commented Sep 23, 2015 at 21:50
A rank 0 tensor is a scalar.
秩为 0 的张量是标量。
A rank 1 tensor is a row or column vector.
秩为 1 的张量是行向量或列向量。
A rank 2 tensor is a matrix, often square.
秩为 2 的张量是矩阵,通常是方阵。
A rank 3 tensor? Think 3D matrix. Instead of a rectangle with data entries for each column and row, think of a cube.
秩为 3 的张量呢?想象一个三维矩阵。不用再想每行每列都有数据的矩形,而是想象一个立方体。
Rank 4… go 4D!
秩为 4 的张量…… 就想象四维的情况吧!
edited Sep 21, 2015 at 13:07
answered Sep 21, 2015 at 2:11 zahbaz (edited by psmears)
Matrices are a special type of tensor, rank 2. Scalars, vectors, matrices, are all tensors.
矩阵是一种特殊类型的张量,秩为 2。标量、向量、矩阵都是张量。
Honestly, tensors are so general that the vast majority of things you deal with in your class are tensors.
老实说,张量是如此普遍,你在课堂上处理的绝大多数事情都是张量。
answered Sep 21, 2015 at 2:15 user223391
张量及其特例:标量、向量与矩阵
1. 张量的基本概念
1.1 张量的定义
张量是一个用于表示多维数据和关系的数学对象,可被视为多维数组的抽象。其核心特征是阶数(order,有时也称为 “秩”),即描述张量元素所需的索引数量。
1.2 张量的普遍性
- 张量在数学、物理、工程及计算机科学(尤其是深度学习)中广泛应用,可表示输入数据、权重、物理量(如应力、电磁场)等。
- 在科学课程中,许多常见对象本质上是张量,例如线性代数中的矩阵、物理学中的向量场、深度学习中的多维数组等。
2. 张量的阶数与特例
张量的阶数由其维度数量(即索引数量)决定,不同阶数的张量对应着我们熟悉的数学对象:
| 张量阶数 | 对应数学对象 | 定义与特征 |
|---|---|---|
| 0 阶 | 标量 | - 单个数字,无维度 - 无索引,如温度(25℃)、质量(5kg) |
| 1 阶 | 向量 | - 一维数组,需 1 个索引定位元素 - 可表示为行向量或列向量,如 [ a 1 , a 2 , a 3 ] \begin{bmatrix} a_1, a_2, a_3 \end{bmatrix} [a1,a2,a3] 或 [ a 1 a 2 a 3 ] \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} a1a2a3 |
| 2 阶 | 矩阵 | - 二维数组,需 2 个索引(行索引
i
i
i、列索引
j
j
j)定位元素 - 表示为 m × n m \times n m×n 的二维结构, m m m 和 n n n 可不等(矩形矩阵),也可相等(正方形矩阵) - 数学符号记为 A i j A_{ij} Aij |
| 3 阶及以上 | 高阶张量 | - 三维及以上数组,需 3 个及以上索引定位元素 - 可类比为 “立方体”(3 阶)或更高维结构,如深度学习中的批量图像数据(样本数 × 高度 × 宽度 × 通道数,4 阶张量) |
3. “阶数” 与 “矩阵的秩”
- 张量的阶数:描述张量的维度数量(索引数量),是张量的固有属性(如矩阵必为 2 阶张量)。
- 线性代数中 “矩阵的秩”:指矩阵中线性独立的行(或列)向量的最大数量,是一个标量值(如 3 × 4 3 \times 4 3×4 矩阵的秩最大为 3)。
注意:为避免混淆,张量语境中通常用 “阶数”(order)而非 “秩” 来描述维度数量。
总结
标量、向量和矩阵都可以被视为张量的特例。
-
张量的阶数由其维度数量(索引数量)决定,是描述多维数据的通用工具。
-
区分“张量的阶数”与“矩阵的秩”是理解张量概念的关键。
-
标量:标量是零维数组,没有索引,秩为 0。它是一个单独的数字,例如温度(25℃)或质量(5kg)。
-
向量:向量是一维数组,有一个索引,秩为 1。它可以表示为行向量或列向量,例如 [ a 1 a 2 a 3 ] \begin{bmatrix} a_1 & a_2 & a_3 \end{bmatrix} [a1a2a3] 或 [ a 1 a 2 a 3 ] \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} a1a2a3 。
-
矩阵:矩阵是二维数组,有两个索引,秩为 2。它是一个 m × n m \times n m×n 的二维结构,例如 [ a 11 a 12 a 21 a 22 ] \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} [a11a21a12a22]。
因此,标量、向量和矩阵都可以看作是张量的特例,分别对应 0 阶、1 阶和 2 阶张量。
via:
-
What’s the difference between a matrix and a tensor? | by Steven Steinke | Medium
https://medium.com/@quantumsteinke/whats-the-difference-between-a-matrix-and-a-tensor-4505fbdc576c -
Difference Between Scalar, Vector, Matrix and Tensor - GeeksforGeeks
https://www.geeksforgeeks.org/machine-learning/difference-between-scalar-vector-matrix-and-tensor/ -
matrices - What are the Differences Between a Matrix and a Tensor? -asked Jun 5, 2013 at 21:52 Aurelius
https://math.stackexchange.com/questions/412423/what-are-the-differences-between-a-matrix-and-a-tensor -
machine learning - Why the sudden fascination with tensors? - Cross Validated edited Jul 4, 2016 at 5:30
https://stats.stackexchange.com/questions/198061/why-the-sudden-fascination-with-tensors -
linear algebra - Qualitatively, what is the difference between a matrix and a tensor? - asked Sep 21, 2015 at 1:49 Life_student
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor





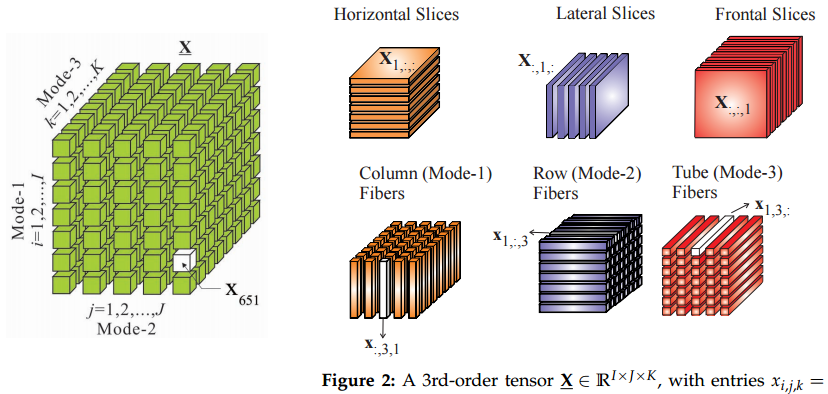
















 4542
4542

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








