注:本文为 “微积分 | dx / dy / ∆x / h” 相关讨论辨析合辑。
英文引文,机翻未校。
中文引文,略作重排。
如有内容异常,请看原文。
But what is “dx” really? Calculus terms explained
But what is “dx” really? Calculus terms explained
“dx” 到底是什么呢?微积分术语讲解
By Jane
The symbol “dx” comes up everywhere in calculus. For example:
符号 “dx” 在微积分中无处不在。例如:
- If
y
y
y is a function of
x
x
x, then we sometimes write the derivative of
y
y
y with respect to
x
x
x as the following:
如果 y y y 是 x x x 的函数,那么我们有时会将 y y y 关于 x x x 的导数写作如下形式:
d y d x \frac{dy}{dx} dxdy
- When we write indefinite integrals, they are written as:
当我们书写不定积分时,其形式如下:
∫ f ( x ) d x \int f(x) \, dx ∫f(x)dx
- When we write definite integrals, they are written as:
当我们书写定积分时,其形式如下:
∫ a b f ( x ) d x \int_{a}^{b} f(x) \, dx ∫abf(x)dx
But what is “dx” really? It’s more than just notation! In this post, we’ll explore the meaning of “dx” and try to get a better understanding of some of the symbols that we often see in calculus.
但 “dx” 究竟是什么呢?它不仅仅是一个符号!在本文中,我们将探讨 “dx” 的含义,并尝试更好地理解我们在微积分中经常看到的一些符号。
Calculus as the study of infinitesimal change
微积分作为对无穷小变化的研究
Calculus is the study of continuous change, or infinitesimal change. To get an idea of what this means, let’s consider the following: suppose that you’re running a race. You begin running at time
x
=
0
x = 0
x=0 seconds and then track your displacement as a function
f
(
x
)
f(x)
f(x). Your displacement function
f
(
x
)
f(x)
f(x) is then a continuous function that varies over time.
微积分是研究连续变化或无穷小变化的学科。为了理解这意味着什么,让我们考虑以下情况:假设你正在参加一场赛跑。你在
x
=
0
x = 0
x=0 秒时开始跑步,然后将你的位移表示为函数
f
(
x
)
f(x)
f(x)。那么你的位移函数
f
(
x
)
f(x)
f(x) 就是一个随时间变化的 连续 函数。
Suppose now that you wanted to know your speed at time
x
=
10
x = 10
x=10 seconds. That is a calculus question since you are looking for a rate of change at one particular time. How could you do this? Well, you might estimate your speed at time
t
=
10
t = 10
t=10 as our average speed between time
x
=
10
x = 10
x=10 and
x
=
11
x = 11
x=11, which can be expressed as:
假设现在你想知道你在
x
=
10
x = 10
x=10 秒时的速度。这是一个微积分问题,因为你正在寻找某一特定时刻的变化率。你该如何做到这一点呢?你可以通过计算
x
=
10
x = 10
x=10 秒到
x
=
11
x = 11
x=11 秒之间的平均速度来估算你在
t
=
10
t = 10
t=10 秒时的速度,这可以表示为:
f ( 11 ) − f ( 10 ) 11 − 10 \frac{f(11) - f(10)}{11 - 10} 11−10f(11)−f(10)
But you could get a better estimate by choosing a smaller time interval, say from
x
=
10
x = 10
x=10 to
x
=
10.1
x = 10.1
x=10.1 instead, or even better from
x
=
10
x = 10
x=10 to
x
=
10.01
x = 10.01
x=10.01.
但你可以通过选择更小的时间间隔来获得更好的估算,比如从
x
=
10
x = 10
x=10 到
x
=
10.1
x = 10.1
x=10.1,或者更好的是从
x
=
10
x = 10
x=10 到
x
=
10.01
x = 10.01
x=10.01。
Really, what you want to do is to take the limit as the size of your time interval goes to zero. That is, you want to take an infinitesimally small change in
x
x
x. Then, by the definition of a derivative, your speed at
x
=
10
x = 10
x=10 seconds is:
实际上,你真正想要做的是取时间间隔趋于零的极限。也就是说,你想要取一个无穷小的变化量
x
x
x。那么,根据导数的定义,你在
x
=
10
x = 10
x=10 秒时的速度为:
f ′ ( 10 ) = lim h → 0 f ( 10 + h ) − f ( 10 ) ( 10 + h ) − 10 = lim h → 0 f ( 10 + h ) − f ( 10 ) h f'\left( 10 \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f(10+h)-f(10)}{\left( 10+h \right)-10}=\underset{h\to 0}{\mathop{\lim }}\,\frac{f(10+h)-f(10)}{h} f′(10)=h→0lim(10+h)−10f(10+h)−f(10)=h→0limhf(10+h)−f(10)
We should think of
h
h
h going to zero as taking smaller and smaller increases in
x
x
x when we take the average speed from time
x
=
10
x = 10
x=10 to time
x
=
10
+
h
x = 10 + h
x=10+h.
我们应该将
h
h
h 趋于零视为在计算从时间
x
=
10
x = 10
x=10 到时间
x
=
10
+
h
x = 10 + h
x=10+h 的平均速度时,取越来越小的
x
x
x 的增量。
This is where “dx” comes in.
这就是 “dx” 发挥作用的地方
“dx” is an infinitesimal change in
x
x
x. We can think of “dx” (read as dee-ex) as an infinitesimally small change in
x
x
x. The “d” in “dx” should remind you of a delta
Δ
\Delta
Δ, which is the symbol for change. “dx” has no numerical value. Rather, it captures this idea that occurs a lot in calculus of taking the limit of smaller and smaller interval sizes to figure out something precisely about a continuous function.
“dx” 是
x
x
x 的一个无穷小变化。 我们可以将 “dx”(读作dee-ex)视为
x
x
x 的一个无穷小变化。 “dx” 中的 “d” 应该让你想起表示变化的符号 delta
Δ
\Delta
Δ。“dx” 没有数值。相反,它捕捉了微积分中一个常见的思想,即通过取越来越小的区间大小的极限,来精确地了解一个连续函数的某一方面。
We can see this if we revisit our speed example from earlier. When computing our derivative
我们可以通过回顾前面的速度例子来理解这一点。当我们计算导数时
f ′ ( 10 ) = lim h → 0 f ( 10 + h ) − f ( 10 ) ( 10 + h ) − 10 f'\left( 10 \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f(10+h)-f(10)}{\left( 10+h \right)-10} f′(10)=h→0lim(10+h)−10f(10+h)−f(10)
The bottom of this fraction is
(
10
+
h
)
−
10
(10 + h) - 10
(10+h)−10 as
h
h
h goes to zero, which is an infinitesimally small change in
x
x
x. We might therefore think of the denominator as
h
h
h goes to zero as
d
x
dx
dx. If we let
y
=
f
(
x
)
y = f(x)
y=f(x), then the numerator of this fraction is
f
(
10
+
h
)
−
f
(
10
)
f(10 + h) - f(10)
f(10+h)−f(10) as
h
h
h goes to zero, which is an infinitesimally small change in
y
y
y, or
d
y
dy
dy. Putting this all together, we recover the notation:
这个分数的分母是
(
10
+
h
)
−
10
(10 + h) - 10
(10+h)−10,当
h
h
h 趋于零时,它是一个无穷小的变化量
x
x
x。因此,我们可以将分母视为当
h
h
h 趋于零时的
d
x
dx
dx。如果我们设
y
=
f
(
x
)
y = f(x)
y=f(x),那么这个分数的分子就是
f
(
10
+
h
)
−
f
(
10
)
f(10 + h) - f(10)
f(10+h)−f(10),当
h
h
h 趋于零时,它是一个无穷小的变化量
y
y
y,即
d
y
dy
dy。将所有这些放在一起,我们得到了以下表示法:
f ′ ( 10 ) = d y d x f'\left( 10 \right)=\frac{dy}{dx} f′(10)=dxdy
That is, the derivative of
f
(
x
)
f(x)
f(x) is the quotient of an infinitesimal change in
y
y
y over an infinitesimal change in
x
x
x. Put more precisely, it is exactly the limit of the change in
y
y
y over the change in
x
x
x over smaller and smaller changes in
x
x
x. The “dx” and “dy” notation just captures this limiting procedure and expresses it as an infinitesimal change in
x
x
x or
y
y
y instead.
也就是说,
f
(
x
)
f(x)
f(x) 的导数是
y
y
y 的无穷小变化量与
x
x
x 的无穷小变化量的比值。更精确地说,它正是当
x
x
x 的变化量越来越小时,
y
y
y 的变化量与
x
x
x 的变化量的比值的极限。“dx” 和 “dy” 的表示法仅仅是捕捉了这个取极限的过程,并将其表示为
x
x
x 或
y
y
y 的无穷小变化量。
“dx” as seen in integrals
在积分中看到的 “dx”
Another place where “dx” is often seen is in integrals. Let’s focus on definite integrals. What does “dx” mean in a definite integral?
“dx” 经常出现在积分中。我们来关注定积分。“dx” 在定积分中是什么意思呢?
∫ a b f ( x ) d x \int_{a}^{b} f(x) \, dx ∫abf(x)dx
“dx” here is still an infinitesimal change in
x
x
x. To see why it’s there, we should think of the integral as a signed area and as the limit of Riemann sums. We recall that to compute a left Riemann sum of
f
(
x
)
f(x)
f(x) from
x
=
a
x = a
x=a to
x
=
b
x = b
x=b with
n
n
n intervals, we let the following be true:
在这里,“dx” 仍然是
x
x
x 的一个无穷小变化。要理解它为什么会出现,我们应该将积分视为一个有符号的面积,并视为黎曼和的极限。我们回忆一下,为了计算从
x
=
a
x = a
x=a 到
x
=
b
x = b
x=b 的
f
(
x
)
f(x)
f(x) 的左黎曼和,且分为
n
n
n 个区间,我们设以下内容成立:
Δ x = b − a n \Delta x = \frac{b - a}{n} Δx=nb−a
Then we take:
然后我们取:
∑
x
f
(
x
)
⋅
Δ
x
\sum\nolimits_{x}{f\left( x \right)}\cdot \Delta x
∑xf(x)⋅Δx
…where
x
x
x takes values
……其中
x
x
x 取值为
a
a
a,
a
+
Δ
x
a + \Delta x
a+Δx,
a
+
2
Δ
x
a + 2\Delta x
a+2Δx,…,
a
+
(
n
−
1
)
Δ
x
=
b
−
Δ
x
a + (n - 1)\Delta x = b - \Delta x
a+(n−1)Δx=b−Δx.
Then, as we let
n
n
n go to infinity,
Δ
x
\Delta x
Δx gets smaller and smaller, and the Riemann sum converges in value to the integral, which is the signed area under the curve
f
(
x
)
f(x)
f(x) between
x
=
a
x = a
x=a and
x
=
b
x = b
x=b. The below picture (from the Wikipedia article on Riemann sums) shows this convergence process:
然后,当我们将
n
n
n 趋于无穷大时,
Δ
x
\Delta x
Δx 越来越小,黎曼和的值趋于积分,即曲线
f
(
x
)
f(x)
f(x) 在
x
=
a
x = a
x=a 和
x
=
b
x = b
x=b 之间的有符号面积。下面的图片(来自维基百科关于黎曼和的文章)展示了这个收敛过程:
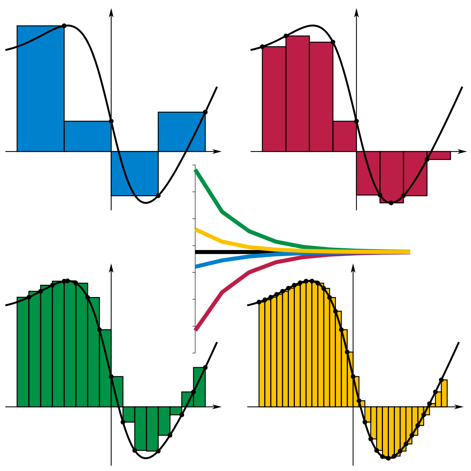
Now, we can see where the notation for the integral comes from. The integral sign
∫
\int
∫ is the continuous version of the sum sign
∑
\sum
∑. The bounds of integration from
a
a
a to
b
b
b are like the first and last
x
x
x values for the summation. And the
d
x
dx
dx is the infinitesimal version of
Δ
x
\Delta x
Δx, what we get when we take smaller and smaller step sizes in
x
x
x.
现在,我们可以看到积分符号的来源。积分符号
∫
\int
∫ 是求和符号
∑
\sum
∑ 的连续版本。积分的上下限
a
a
a 到
b
b
b 就像是求和的首尾
x
x
x 值。而
d
x
dx
dx 是
Δ
x
\Delta x
Δx 的无穷小版本,即当我们在
x
x
x 上取越来越小的步长时得到的结果。
Another way to think about this is that in our integral, we are summing up infinitesimally thin rectangles with height
f
(
x
)
f(x)
f(x) and width
d
x
dx
dx to compute our signed area precisely.
另一种思考方式是,在我们的积分中,我们正在将高度为
f
(
x
)
f(x)
f(x)、宽度为
d
x
dx
dx 的无穷薄矩形相加,以精确地计算我们的有符号面积。
Hopefully, the symbol “dx” is a little less mysterious now!
希望现在 “dx” 这个符号不再那么神秘了!
Using d x dx dx for h h h in the definition of derivative
在导数定义中用 d x dx dx 代替 h h h
edited Oct 26, 2015 at 18:53
DavidButlerUofA
asked Oct 21, 2015 at 13:17
John Molokach
Is it mathematically correct to write
写成下面这样在数学上是正确的吗
f ′ ( x ) = lim d x → 0 f ( x + d x ) − f ( x ) d x f'(x) = \lim_{dx \to 0} \frac{f(x + dx) - f(x)}{dx} f′(x)=limdx→0dxf(x+dx)−f(x),
rather than
而不是
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} f′(x)=limh→0hf(x+h)−f(x)?
If not, what is the difference? If so, why isn’t this notation used from the beginning? My feeling for the latter is that it would align the derivative more with the inverse of the indefinite integral.
如果不正确,区别是什么?如果正确,为什么一开始不使用这种符号呢?我对后者的感觉是,它会使导数与不定积分的逆运算更一致。
edited Oct 26, 2015 at 18:53
asked Oct 21, 2015 at 13:17
John Molokach
For educators: follow the notation in the textbook. Even if both of these are correct, it does not help students at this level to see variant notations.
对教育工作者来说:遵循教科书中的符号。即使这两种符号都是正确的,让这个水平的学生看到不同的符号也没有帮助。
– Gerald Edgar
Commented Oct 21, 2015 at 14:48
In smooth infinitesimal analysis one writes
在光滑无穷小分析中,人们写成
f ( x + d x ) = f ( x ) + f ′ ( x ) d x f(x + dx) = f(x) + f'(x)dx f(x+dx)=f(x)+f′(x)dx,
where
d
x
dx
dx is an infinitesimal, without any limits.
其中
d
x
dx
dx 是一个无穷小量,没有任何极限。
– Dag Oskar Madsen
Commented Oct 21, 2015 at 22:04
@GeraldEdgar I would be more convinced by that if I ever saw any evidence that my students read the textbook, or if I found a textbook that I could wholeheartedly recommend that they read.
@杰拉尔德·埃德加 如果我曾经看到任何证据表明我的学生阅读教科书,或者如果我找到一本我可以全心全意推荐他们阅读的教科书,我会更相信这一点。
– Mike Shulman
Commented Oct 27, 2015 at 5:41
4 Answers
To use
f
′
(
x
)
=
lim
d
x
→
0
f
(
x
+
d
x
)
−
f
(
x
)
d
x
f'(x) = \lim_{dx \to 0} \frac{f(x + dx) - f(x)}{dx}
f′(x)=limdx→0dxf(x+dx)−f(x) is mathematically correct if
d
x
dx
dx is the name for a real variable. (If it should be something else it needs to be made clear what it should be.)
如果
d
x
dx
dx 是一个实变量的名称,那么使用
f
′
(
x
)
=
lim
d
x
→
0
f
(
x
+
d
x
)
−
f
(
x
)
d
x
f'(x) = \lim_{dx \to 0} \frac{f(x + dx) - f(x)}{dx}
f′(x)=limdx→0dxf(x+dx)−f(x) 在数学上是正确的。(如果它应该是其他东西,就需要明确它应该是什么。)
It would also be correct to say
f
′
(
x
)
=
lim
small
→
0
f
(
x
+
small
)
−
f
(
x
)
small
f'(x) = \lim_{\text{small} \to 0} \frac{f(x + \text{small}) - f(x)}{\text{small}}
f′(x)=limsmall→0smallf(x+small)−f(x)
with the understanding that small is the name of a real variable.
说
f
′
(
x
)
=
lim
small
→
0
f
(
x
+
small
)
−
f
(
x
)
small
f'(x) = \lim_{\text{small} \to 0} \frac{f(x + \text{small}) - f(x)}{\text{small}}
f′(x)=limsmall→0smallf(x+small)−f(x) 也是正确的,前提是理解“small”是一个实变量的名称。
An issue I see with what you propose is though that
d
x
dx
dx is not a common notation for a real variable, but rather something else. What exactly
d
x
dx
dx means, depends on the context, but typically it is not used to denote a real number.
不过,我认为你所提议的问题在于,
d
x
dx
dx 不是实变量的常见符号,而是其他东西。
d
x
dx
dx 的确切含义取决于上下文,但通常它不被用来表示实数。
A very related notation that is more common is
一个非常相关且更常见的符号是
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} f′(x)=limΔx→0Δxf(x+Δx)−f(x)
The idea is that the
Δ
x
\Delta x
Δx
is a finite difference, as opposed to an infinitesimal difference that might be denoted by
d
x
dx
dx
(where the latter notion might or might not be made precise).
其想法是,
Δ
x
\Delta x
Δx 是有限差分,与可能用
d
x
dx
dx 表示的无穷小差分相对(后者的概念可能精确,也可能不精确)。
Personally I prefer to use just an
h
h
h
or something similar, to emphasis that it is just some real parameter there nothing special or mysterious. To name it
d
x
dx
dx or
Δ
x
\Delta x
Δx goes counter this so I would not do it.
就我个人而言,我更喜欢只用一个
h
h
h 或类似的东西,以强调它只是某个实参数,没有什么特别或神秘之处。把它命名为
d
x
dx
dx 或
Δ
x
\Delta x
Δx 与此相悖,所以我不会这么做。
– quid
answered Oct 21, 2015 at 14:09
Agreed that it is mathematically correct if
d
x
dx
dx is the name for a real variable. I do use it that way, despite all the
h
h
hs in the textbook, because I think it is important to emphasize that the role played by this variable is that of a small change in
x
x
x. And I think insisting on writing
Δ
x
\Delta x
Δx when the small change is “finite” is misguided pedantry, especially in textbooks that a few sections later on when talking about “differentials” define
d
x
=
Δ
x
dx = \Delta x
dx=Δx!
同意如果
d
x
dx
dx 是实变量的名称,那么它在数学上是正确的。尽管教科书中有很多
h
h
h,我还是这样使用它,因为我认为强调这个变量所扮演的角色是
x
x
x 的微小变化很重要。而且我认为,当微小变化是“有限的”时,坚持写
Δ
x
\Delta x
Δx 是一种误入歧途的迂腐做法,特别是在几节之后谈论“微分”时定义
d
x
=
Δ
x
dx = \Delta x
dx=Δx 的教科书中!
– Mike Shulman
Commented Oct 27, 2015 at 5:35
In the other examples, one can make sense of
d
x
dx
dx in a consistent way: e.g. if we model it as differential forms, then
d
y
d
x
\frac{dy}{dx}
dxdy is a ratio between two differential forms,
∫
sin
x
d
x
\int \sin x dx
∫sinxdx is the anti-derivative of a differential form, and
∫
a
b
sin
x
d
x
\int_a^b \sin x dx
∫absinxdx is the integral of a differential form along a (directed) path. One can even reasonably extend differentiable functions to the exterior algebra, and make literally true statements like
在其他例子中,人们可以以一致的方式理解
d
x
dx
dx:例如,如果我们把它建模为微分形式,那么
d
y
d
x
\frac{dy}{dx}
dxdy 是两个微分形式之间的比率,
∫
sin
x
d
x
\int \sin x dx
∫sinxdx 是微分形式的反导数,而
∫
a
b
sin
x
d
x
\int_a^b \sin x dx
∫absinxdx 是微分形式沿(有向)路径的积分。人们甚至可以合理地将可微函数扩展到外代数,并做出字面上正确的陈述,如
f ( x + d x ) − f ( x ) = f ′ ( x ) d x f(x + dx) - f(x) = f'(x)dx f(x+dx)−f(x)=f′(x)dx
However, if one were to write the calc-1 definition of derivative as
然而,如果有人把微积分 1 中导数的定义写成
lim d x → 0 f ( x + d x ) − f ( x ) d x \lim_{dx \to 0} \frac{f(x + dx) - f(x)}{dx} limdx→0dxf(x+dx)−f(x)
the
d
x
dx
dx here doesn’t represent anything resembling a differential form at all. The superficial similarity to my last remark in the previous paragraph makes things worse, not better, since it would conflate the distinct ideas, and thus make it harder to intuitively arrive at what
d
x
dx
dx means.
这里的
d
x
dx
dx 根本不代表任何类似于微分形式的东西。与我上一段最后一句话的表面相似性使事情变得更糟,而不是更好,因为它会混淆不同的概念,从而使人们更难直观地理解
d
x
dx
dx 的含义。
answered Oct 23, 2015 at 9:54
user797
This definitely sheds some light on the comparison between
h
h
h and
d
x
dx
dx. I suppose that to use the latter in the sense of the definition of the derivative, and defining
d
x
dx
dx as the same differential form as integration, the definition would not make sense since
d
x
dx
dx is already infinitesimally small. That is, we’d get
0
/
0
0/0
0/0 for every derivative when making
d
x
→
0
dx \to 0
dx→0. Is this a right conclusion?
这无疑有助于阐明
h
h
h 和
d
x
dx
dx 之间的比较。我想,在导数定义的意义上使用后者,并将
d
x
dx
dx 定义为与积分相同的微分形式,这个定义是没有意义的,因为
d
x
dx
dx 已经是无穷小的了。也就是说,当让
d
x
→
0
dx \to 0
dx→0 时,每个导数都会得到
0
/
0
0/0
0/0。这是一个正确的结论吗?
– John Molokach
Commented Oct 23, 2015 at 11:38
I disagree that d x dx dx here doesn’t represent anything resembling a differential form. In fact, it resembles a differential form quite a lot! If we free ourselves from insisting that a “differential form” must always depend linearly on d x dx dx, then we can consider f ( x + d x ) − f ( x ) f(x + dx) - f(x) f(x+dx)−f(x) to indeed be a differential form (a function depending on both a variable and a small change in that variable) that is linearly approximated by another differential form d y dy dy
- (essentially by definition of the latter).
我不同意这里的 d x dx dx 不代表任何类似于微分形式的东西。事实上,它非常像微分形式!如果我们不再坚持“微分形式”必须总是线性地依赖于 d x dx dx,那么我们可以认为 f ( x + d x ) − f ( x ) f(x + dx) - f(x) f(x+dx)−f(x) 确实是一个微分形式(一个既依赖于变量又依赖于该变量的微小变化的函数),它由另一个微分形式 d y dy dy 线性近似(本质上是根据后者的定义)。
– Mike Shulman
Commented Oct 27, 2015 at 5:38
A sitenote: When you leave classical analysis and you take non-standard analysis, then you have infinitesimals in your underlying theory (they are part of the so called hyperreals). In this theory you can write
一个旁注:当你离开经典分析并学习非标准分析时,你的基础理论中就会有无穷小量(它们是所谓的超实数的一部分)。在这个理论中,你可以写成
f ( x + d x ) − f ( x ) d x \frac{f(x + dx) - f(x)}{dx} dxf(x+dx)−f(x)
with d x dx dx being an infinitesimal. This gives a number which difference to f ′ ( x ) f'(x) f′(x) is only an infinitesimal (see the comments to this question). No hocus pocus necessary 😉
其中 d x dx dx 是一个无穷小量。这给出了一个与 f ′ ( x ) f'(x) f′(x) 的差仅为无穷小量的数(见对这个问题的评论)。不需要任何戏法;-)
“I think you should be more explicit here in step two.”
from What 's so Funny about Science? by Sidney Harris (1977)
“我认为在第二步中,你应该更加明确.”
科学有什么好笑的?西德尼·哈里斯(1977)
edited Oct 25, 2015 at 23:11
answered Oct 24, 2015 at 14:16
Stephan Kulla
Yes, in non-standard analysis you need no limit to define the derivative. The reason is, that you have infinitesimals which don’t exist in classical analysis and which you can use in the definition of the derivative.
是的,在非标准分析中,你不需要极限来定义导数。原因是,你有在经典分析中不存在的无穷小量,你可以在导数的定义中使用它们。
– Stephan Kulla
Commented Oct 24, 2015 at 14:21
See for more details
- 更多细节参见
- calculus - Why it is absolutely mistaken to cancel out differentials? - Mathematics Stack Exchange
https://math.stackexchange.com/questions/1271476/why-it-is-absolutely-mistaken-to-cancel-out-differentials/1273083
- calculus - Why it is absolutely mistaken to cancel out differentials? - Mathematics Stack Exchange
– Stephan Kulla
Commented Oct 24, 2015 at 14:22
As a side note, for differentiability, the (standard part of the) quotient can’t depend upon which non-zero infinitesimal is used, so it takes at least one explicit quantifier to define the derivative and to make sure it exists in the first place.
作为一个旁注,对于可微性,(的标准部分)商不能依赖于所使用的非零无穷小量,所以首先需要至少一个显式量词来定义导数并确保它存在。
– Vandermonde
Commented Oct 24, 2015 at 16:17
You still need hocus pocus to define the derivative: NSA just picks a different magic (albeit, arguably conceptually simpler magic).
定义导数仍然需要戏法:非标准分析只是选择了一种不同的魔法(尽管可以说在概念上更简单的魔法)。
– user797
Commented Oct 25, 2015 at 9:48
+1, but: let
E
E
E be the expression written in this answer. Note that in NSA,
E
E
E is not the derivative
f
′
(
x
)
f'(x)
f′(x). The derivative equals the standard part of
E
E
E.
+1,但是:让
E
E
E 是本答案中所写的表达式。注意,在非标准分析中,
E
E
E 不是导数
f
′
(
x
)
f'(x)
f′(x)。导数等于
E
E
E 的标准部分。
– user507
Commented Oct 25, 2015 at 21:32
导数中带小 d 的项


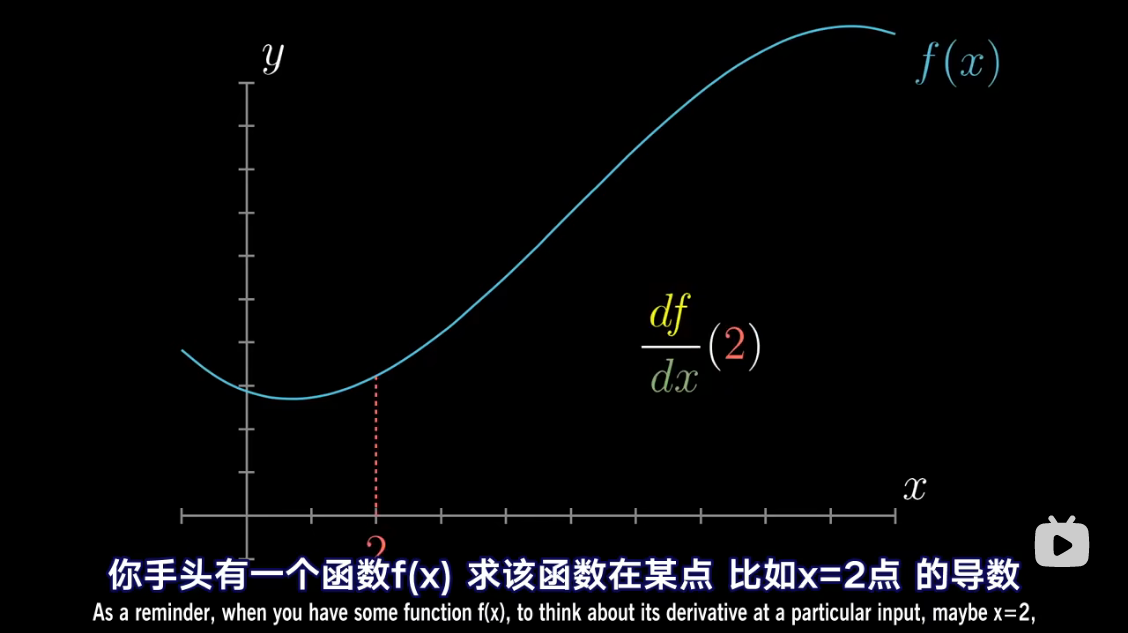
把 d f df df 和 d x dx dx 考虑成具体存在的非零变化量
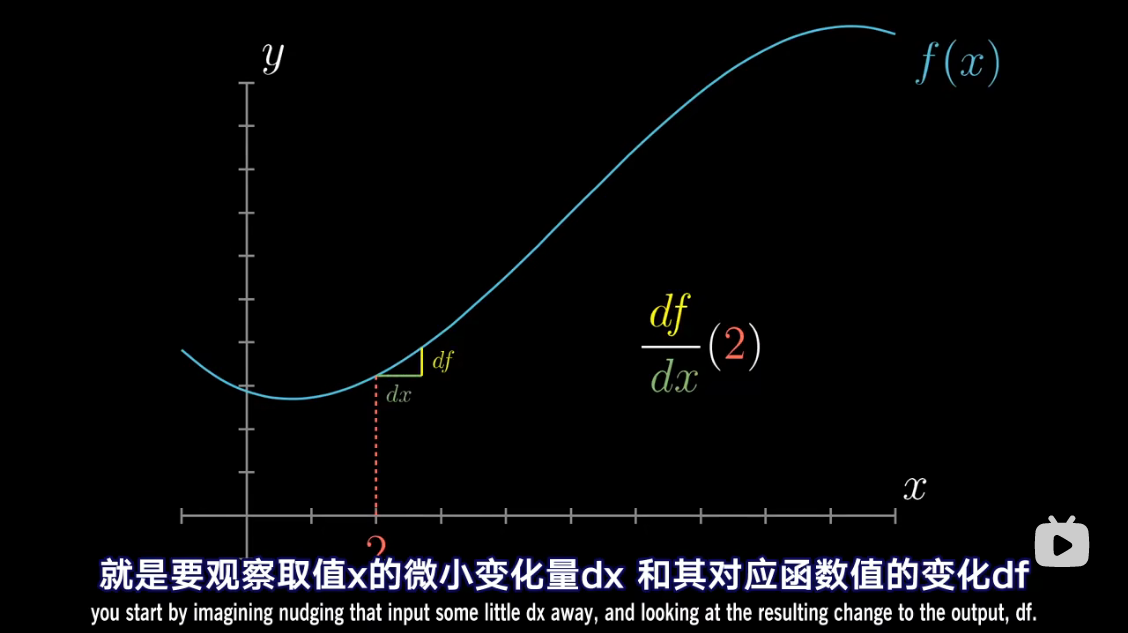
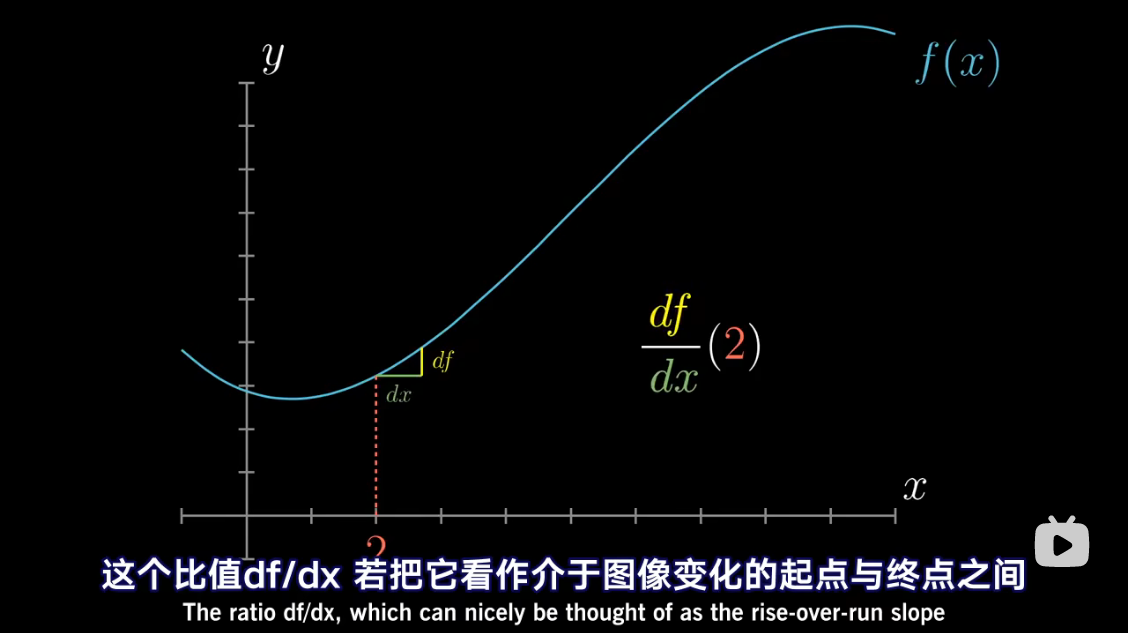
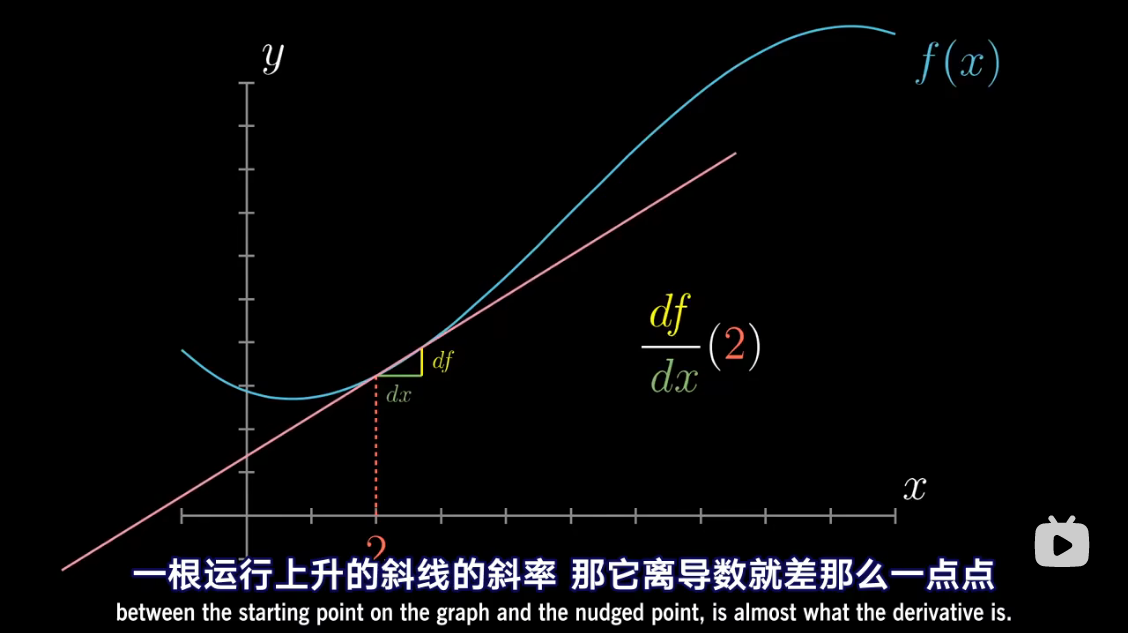
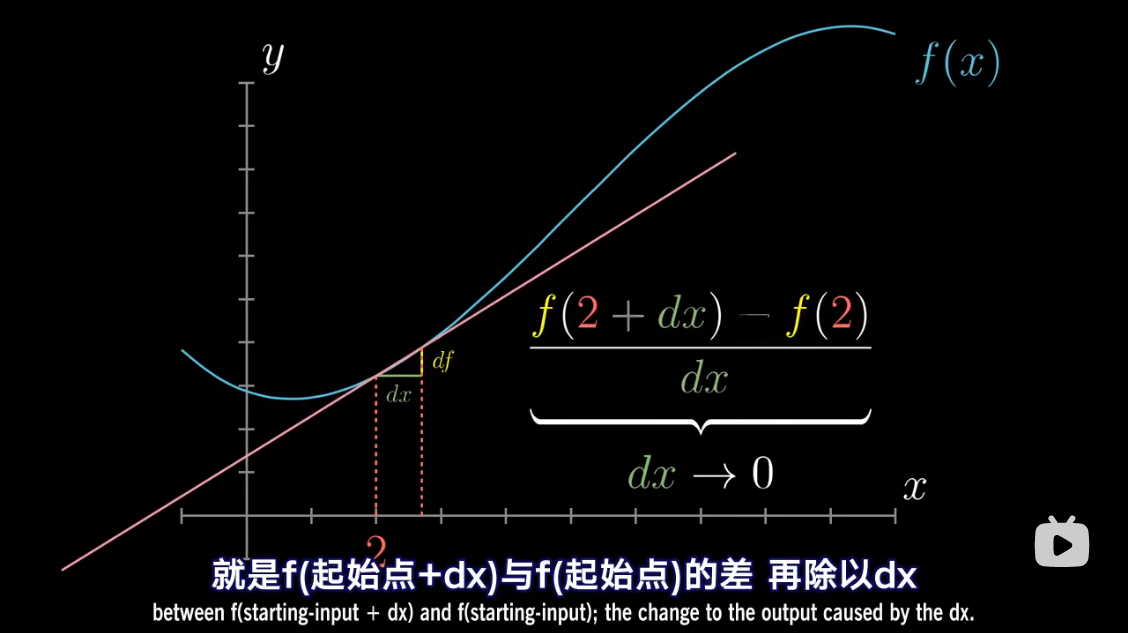
d
x
dx
dx
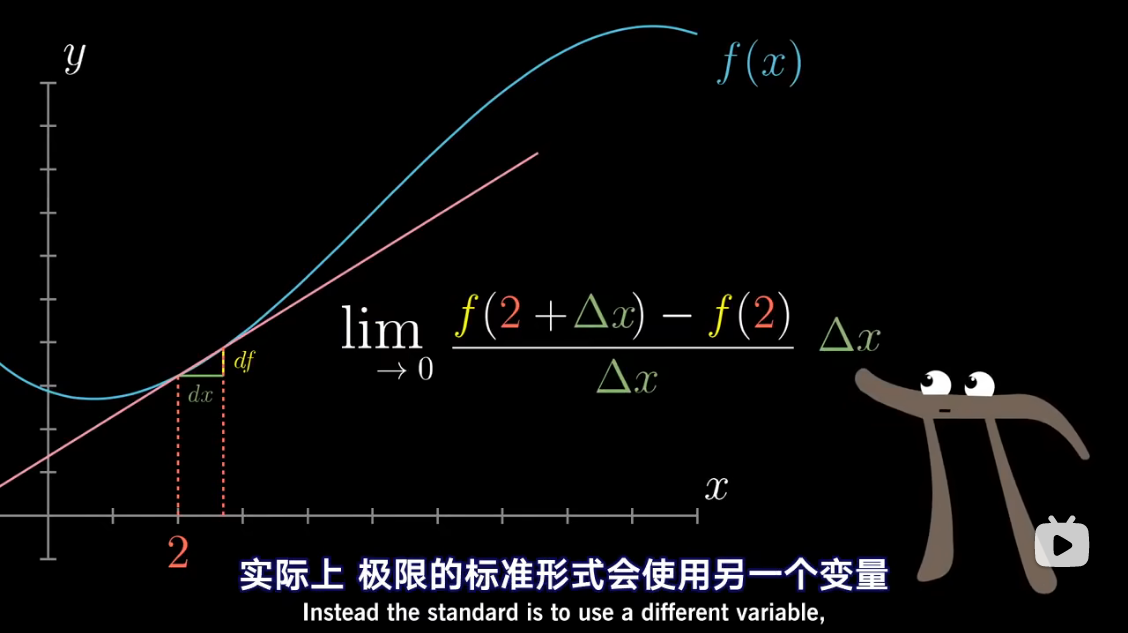
Δ
x
\Delta x
Δx
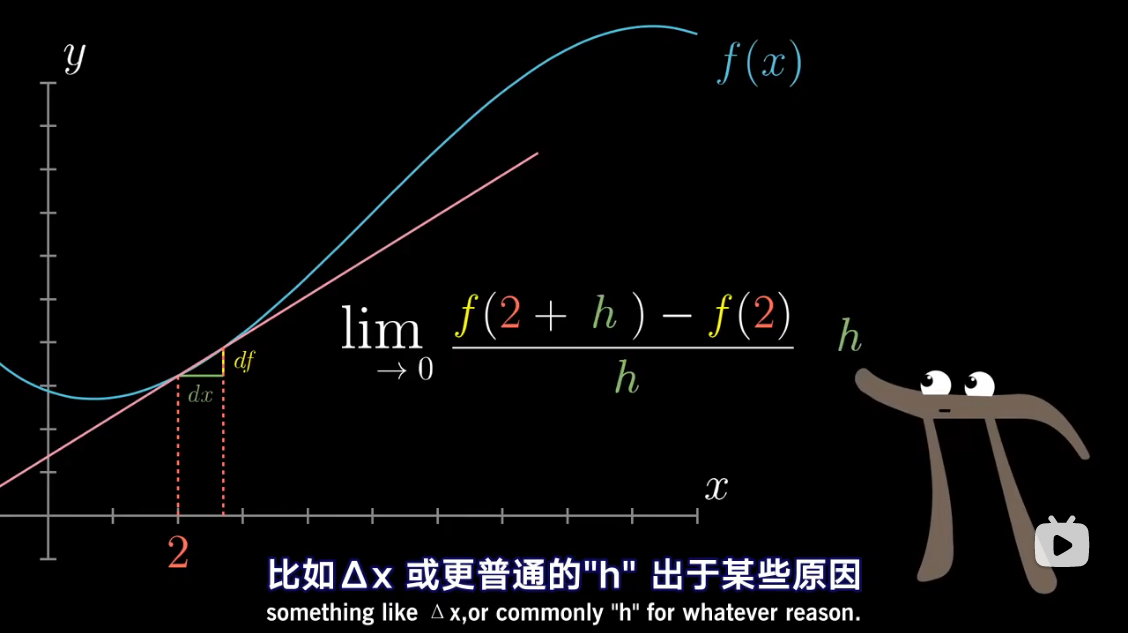
h
h
h
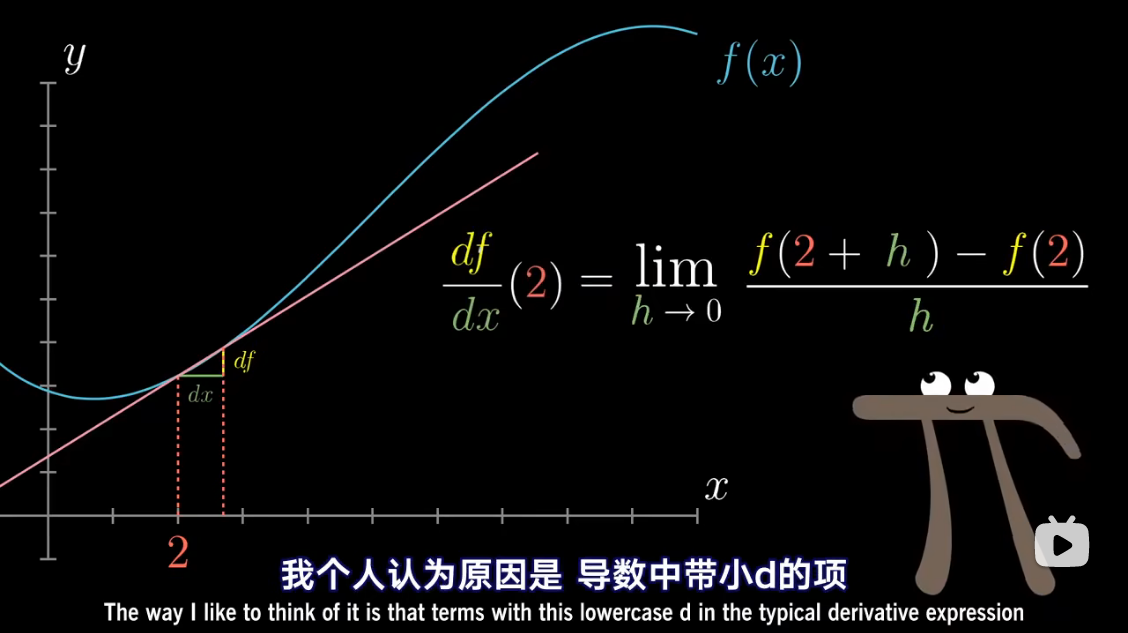
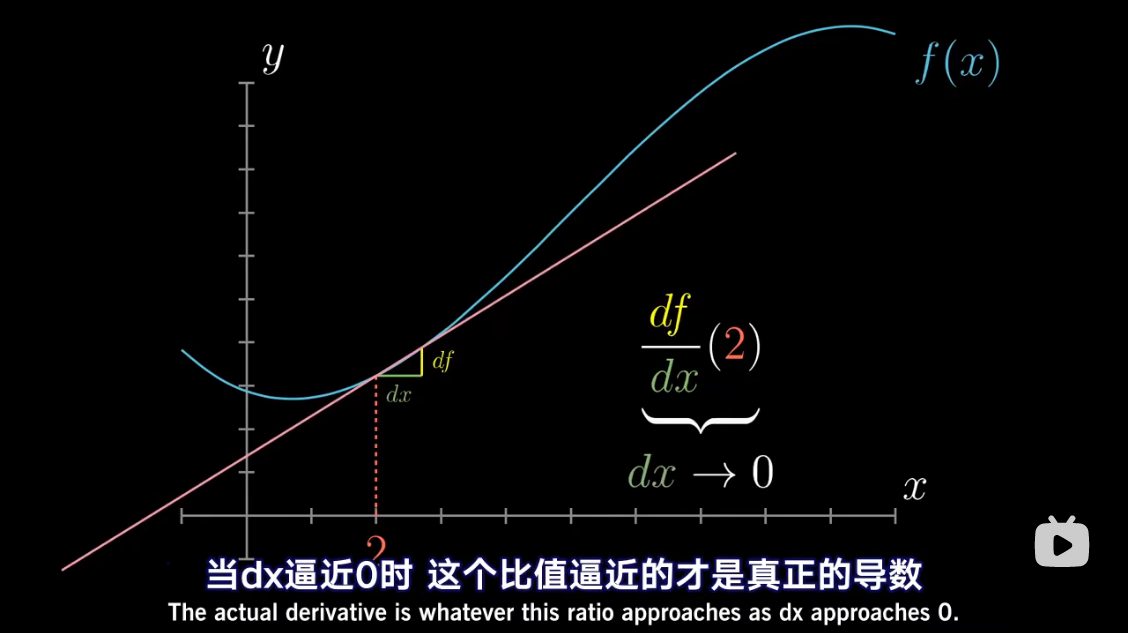
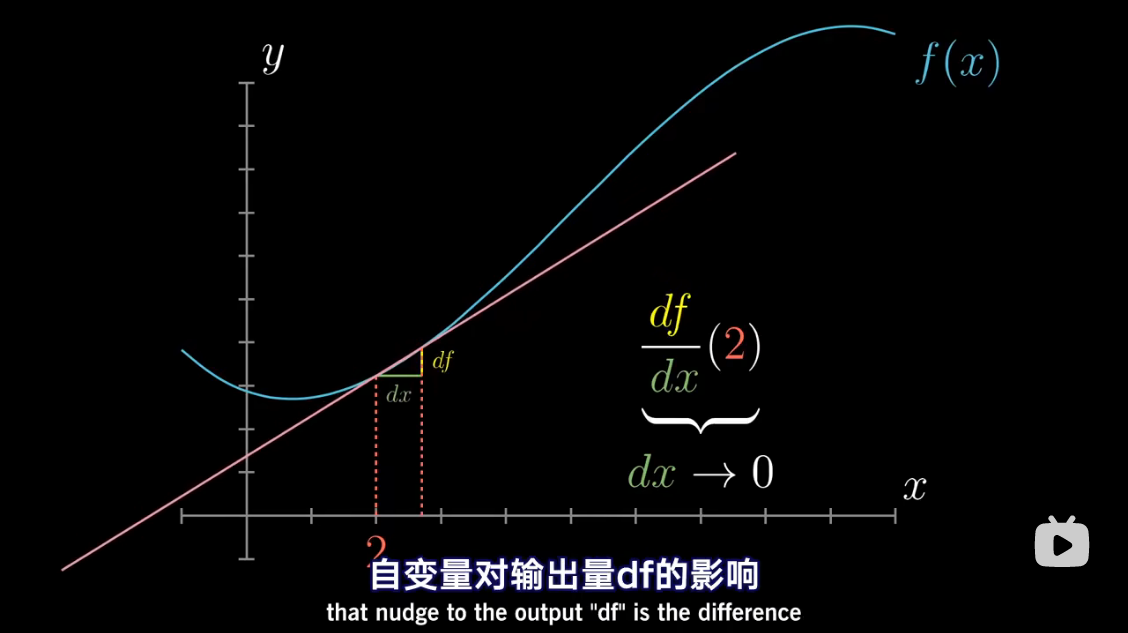
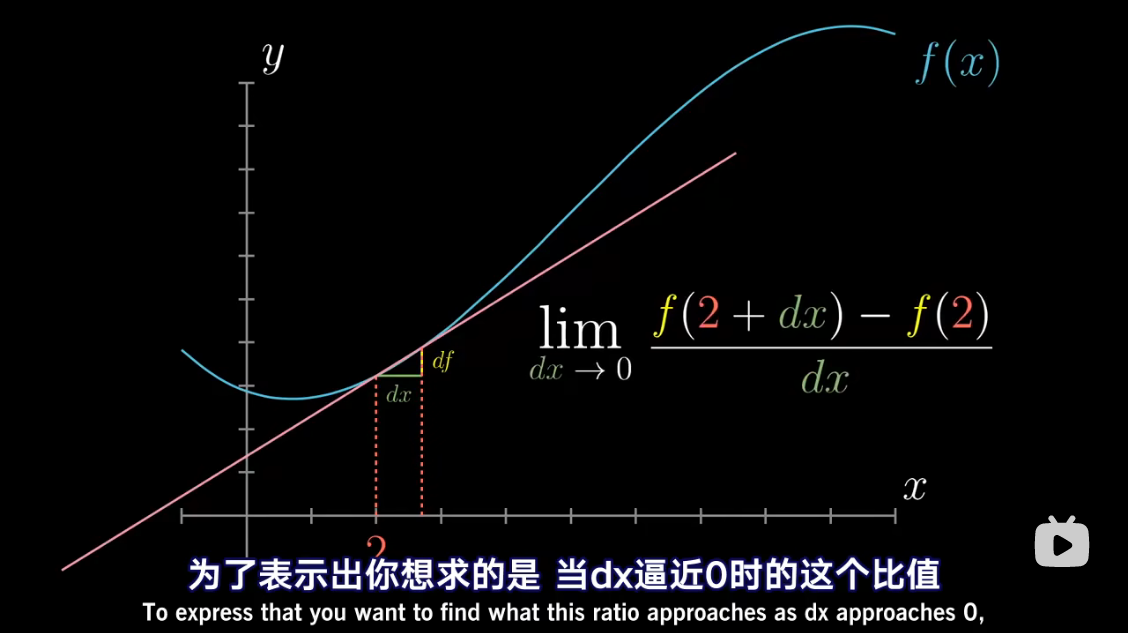
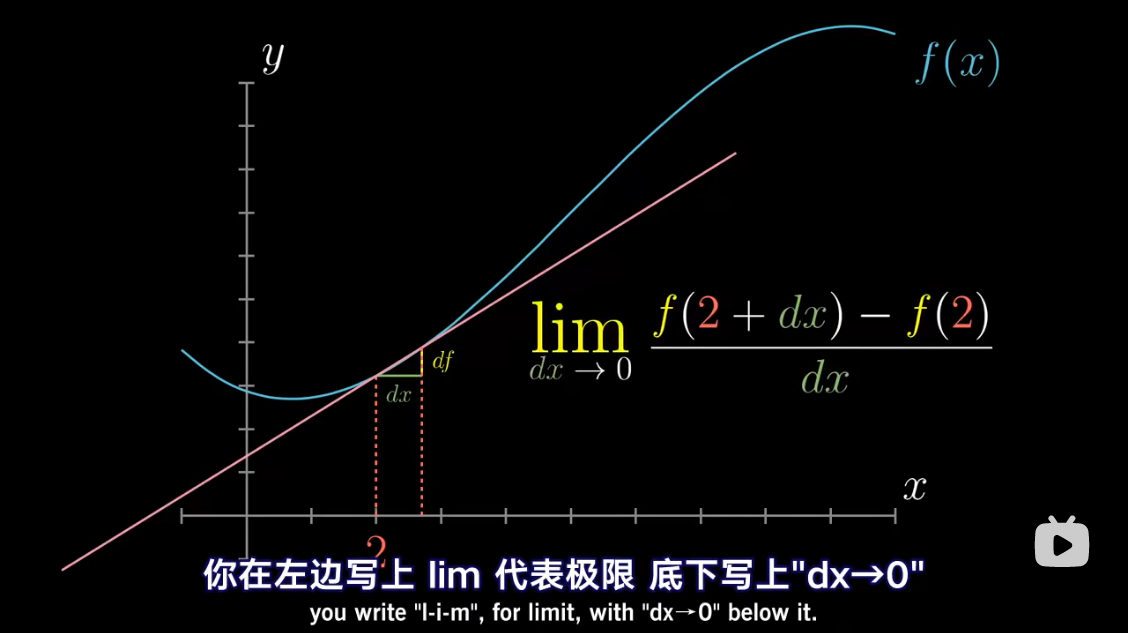
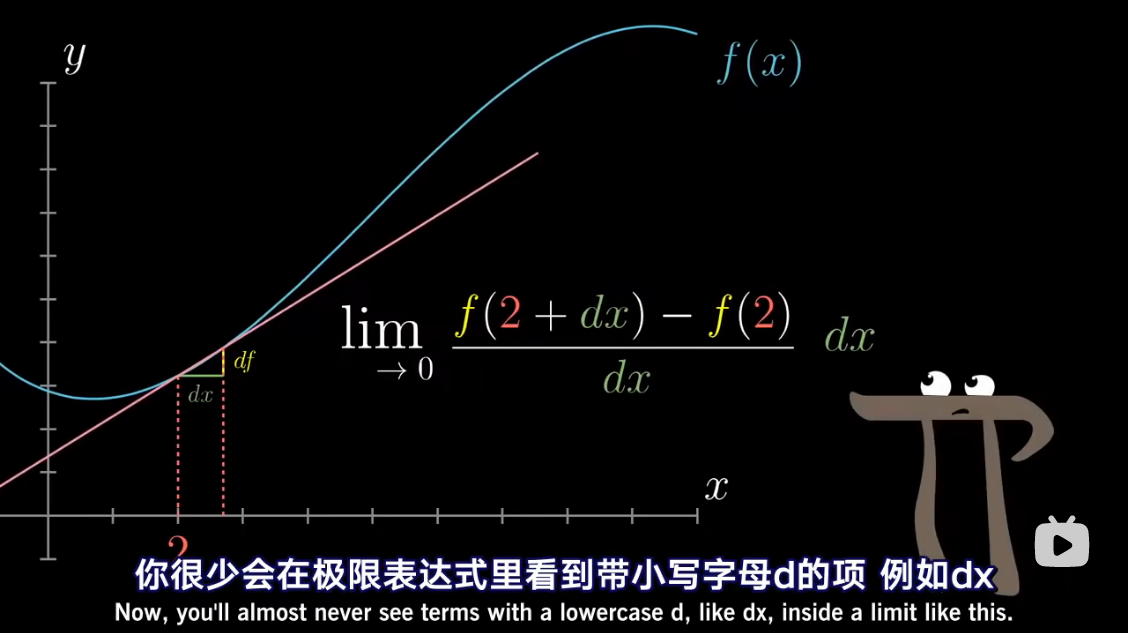
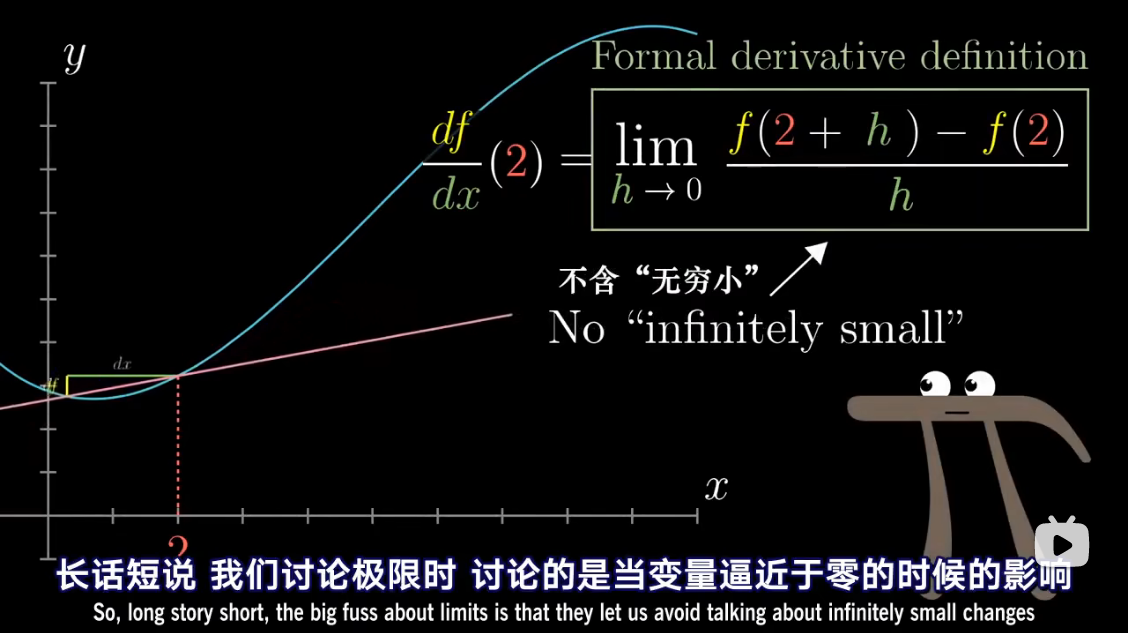
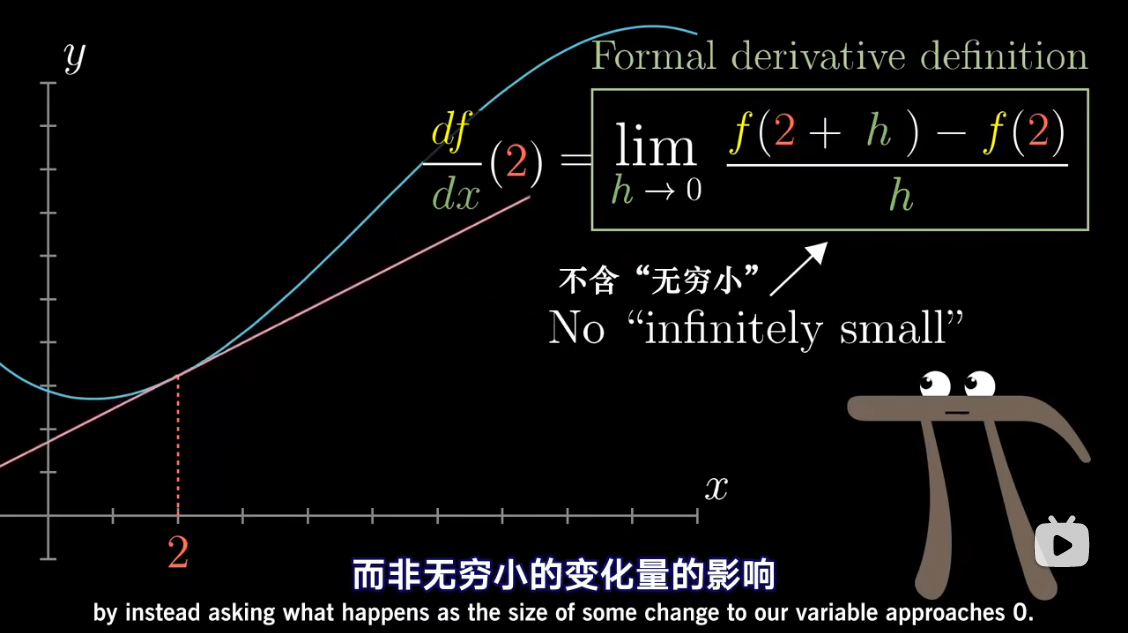
导数中带小 d d d 的项,
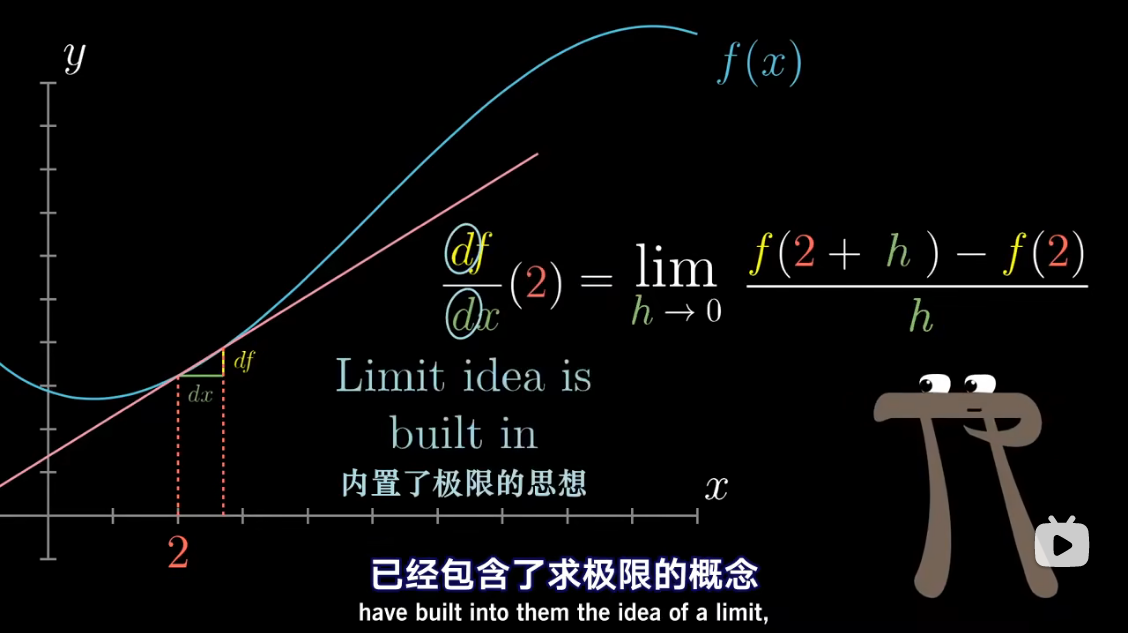
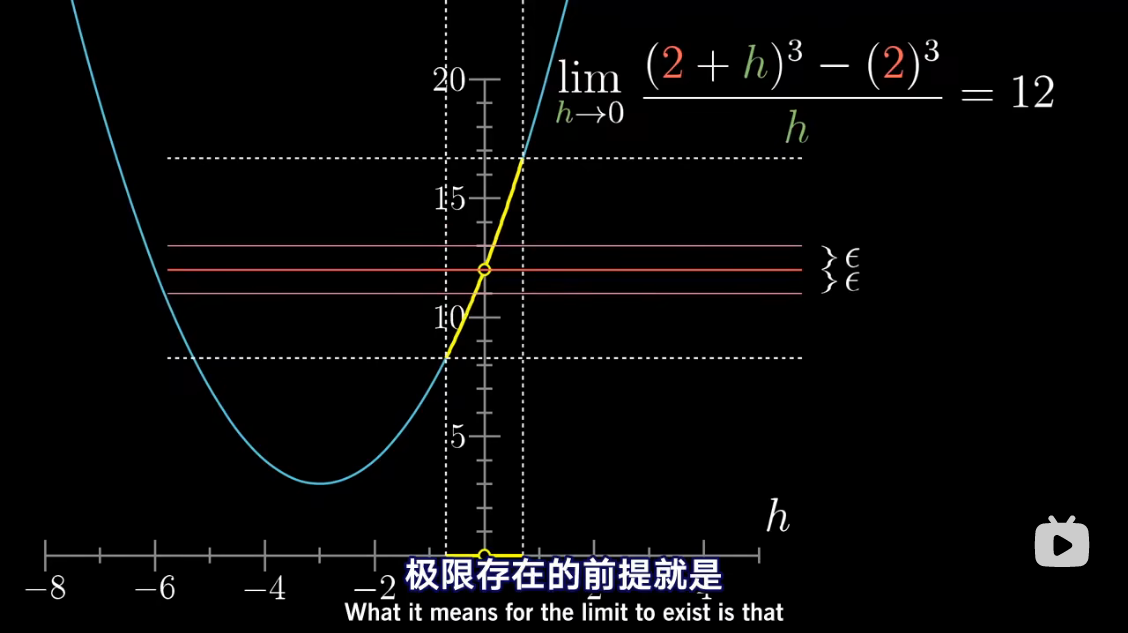
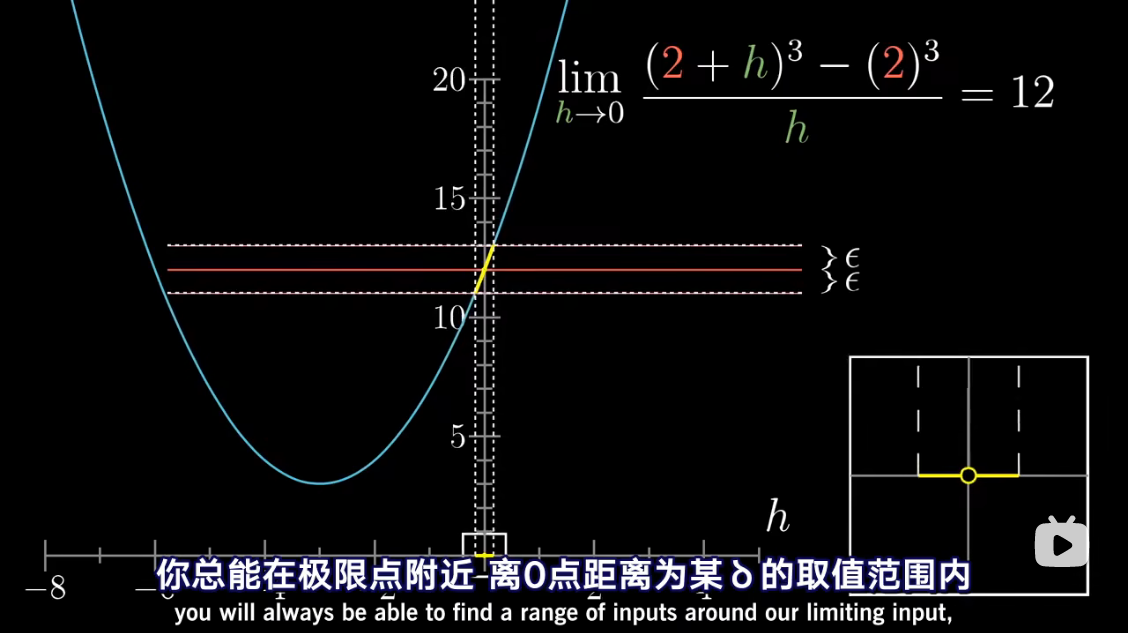
已经包含了求极限的概念
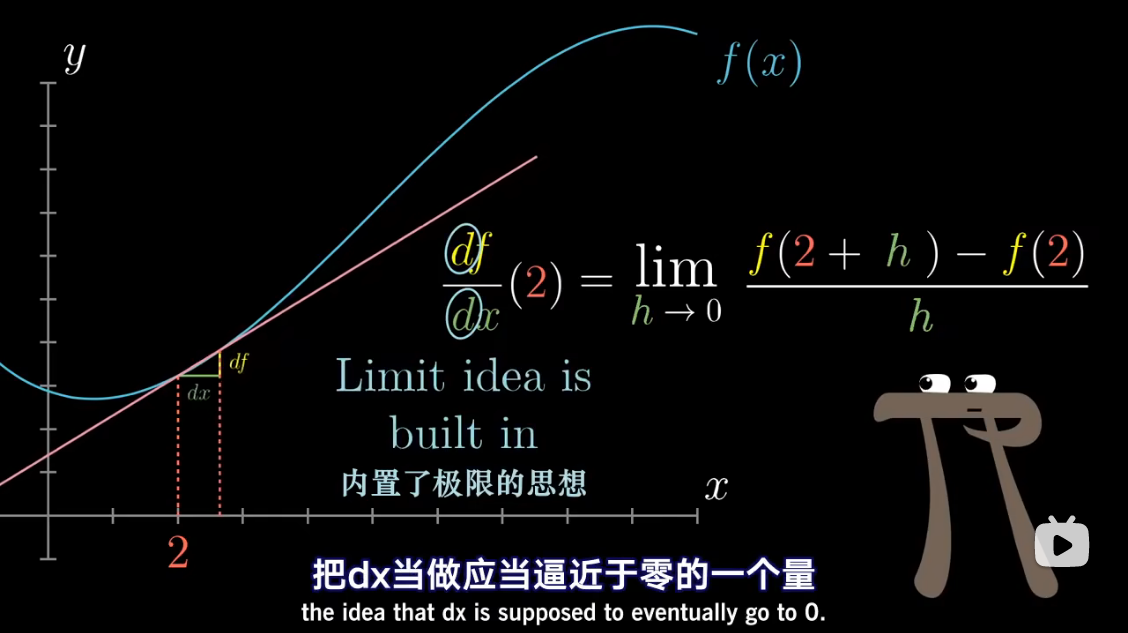
把 d x dx dx 当做应当逼近于零的一个量
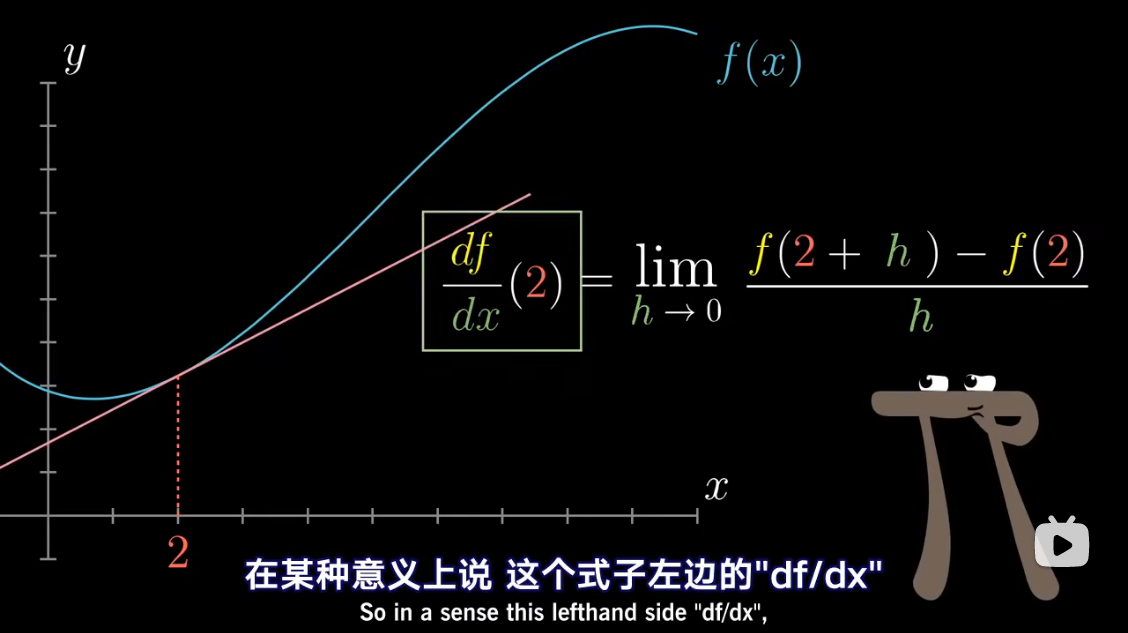
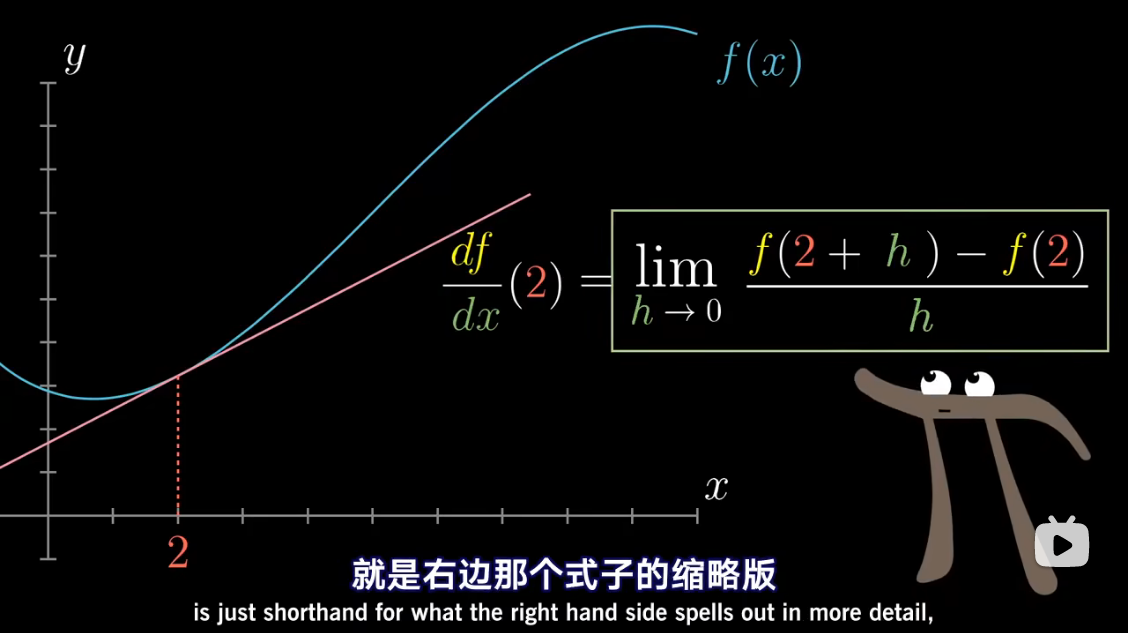
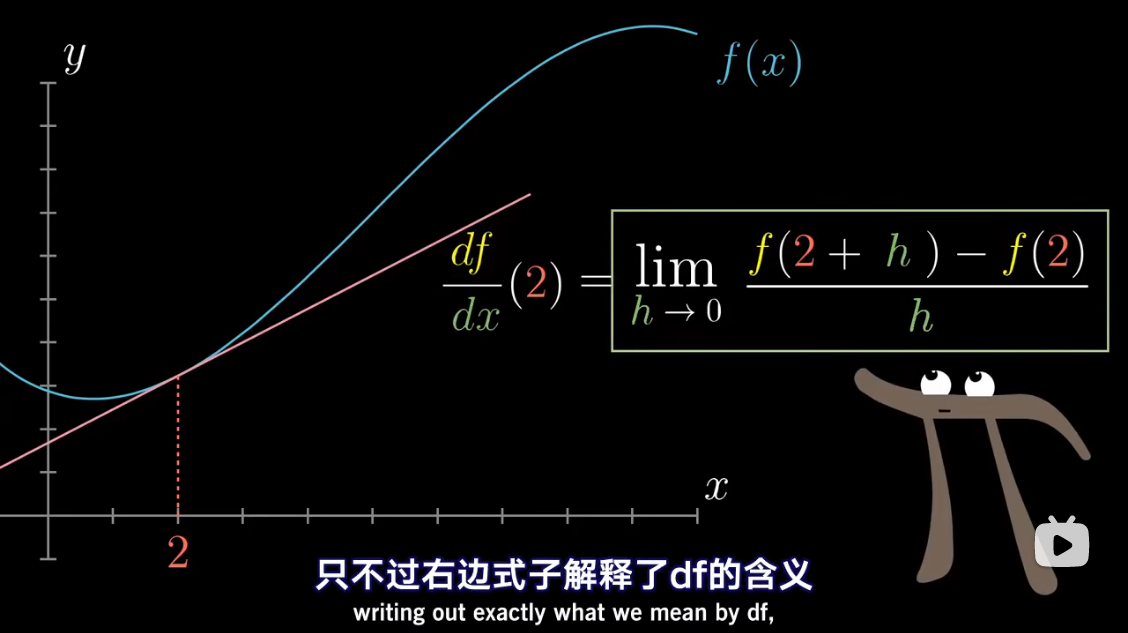
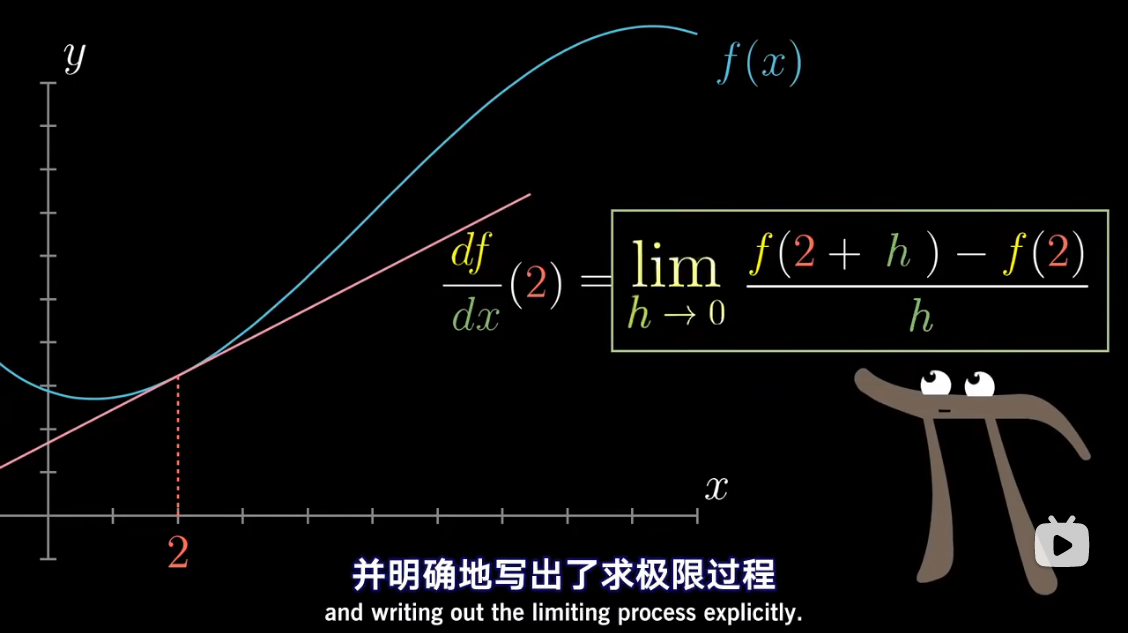
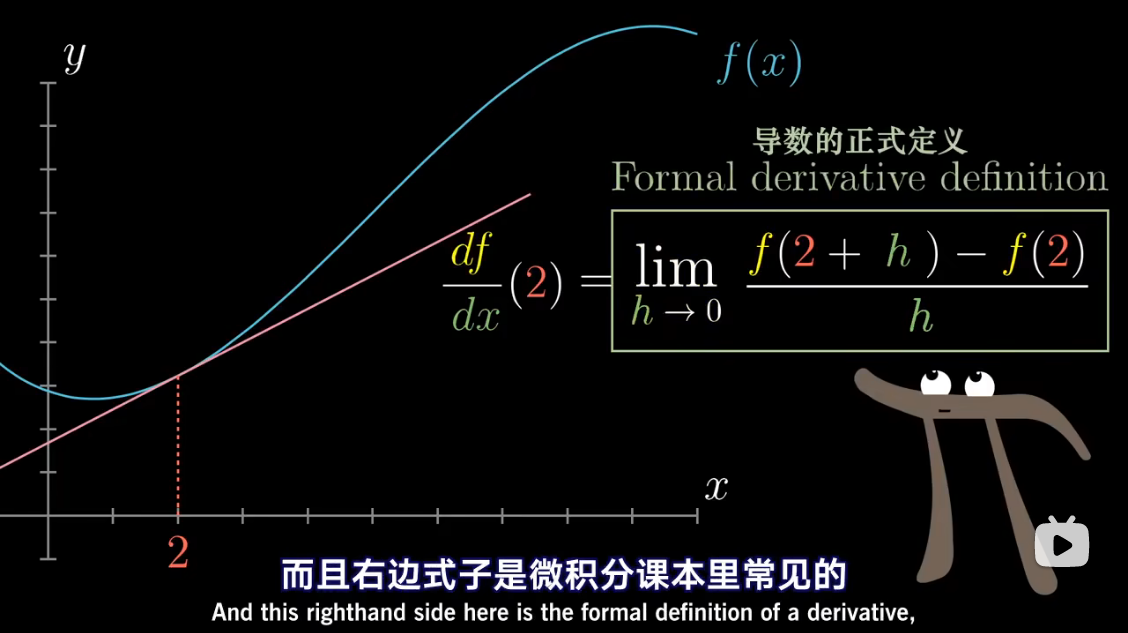
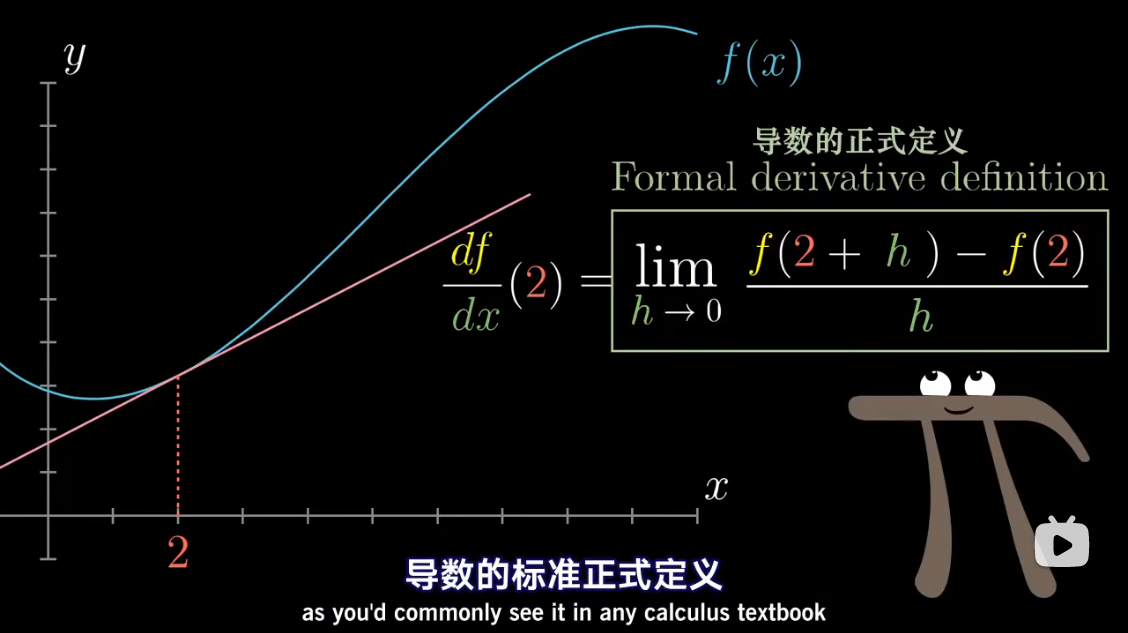
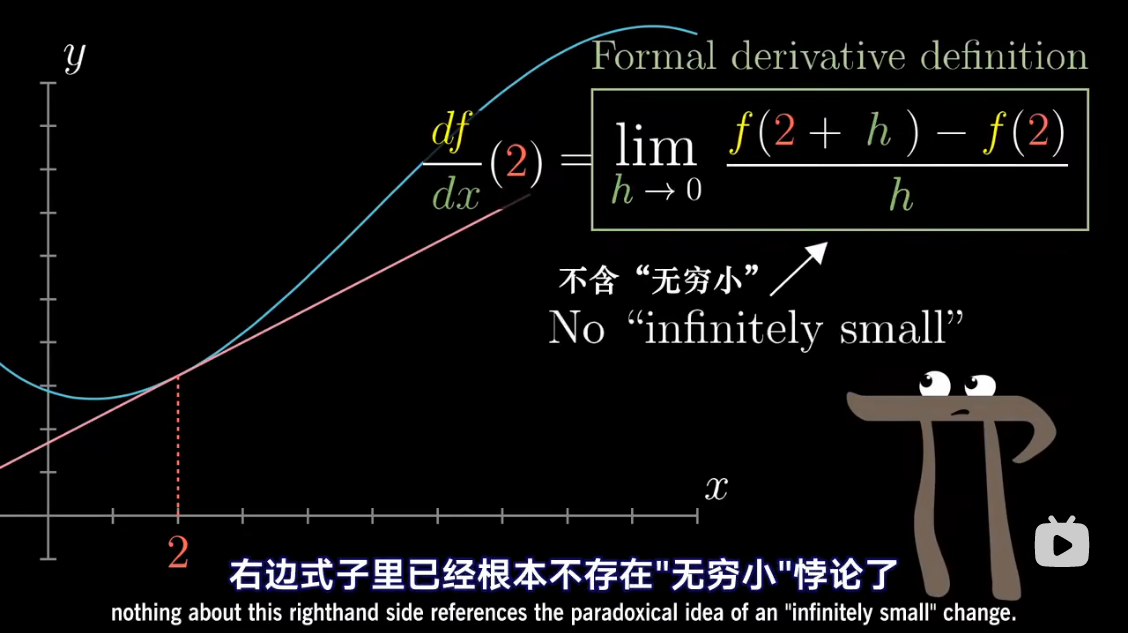
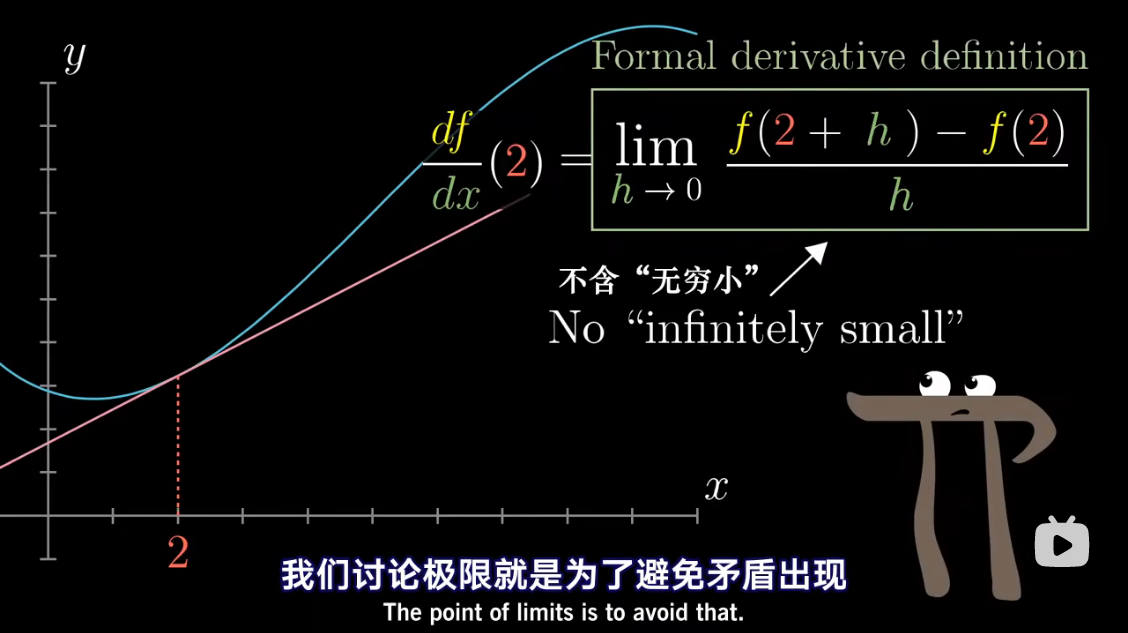
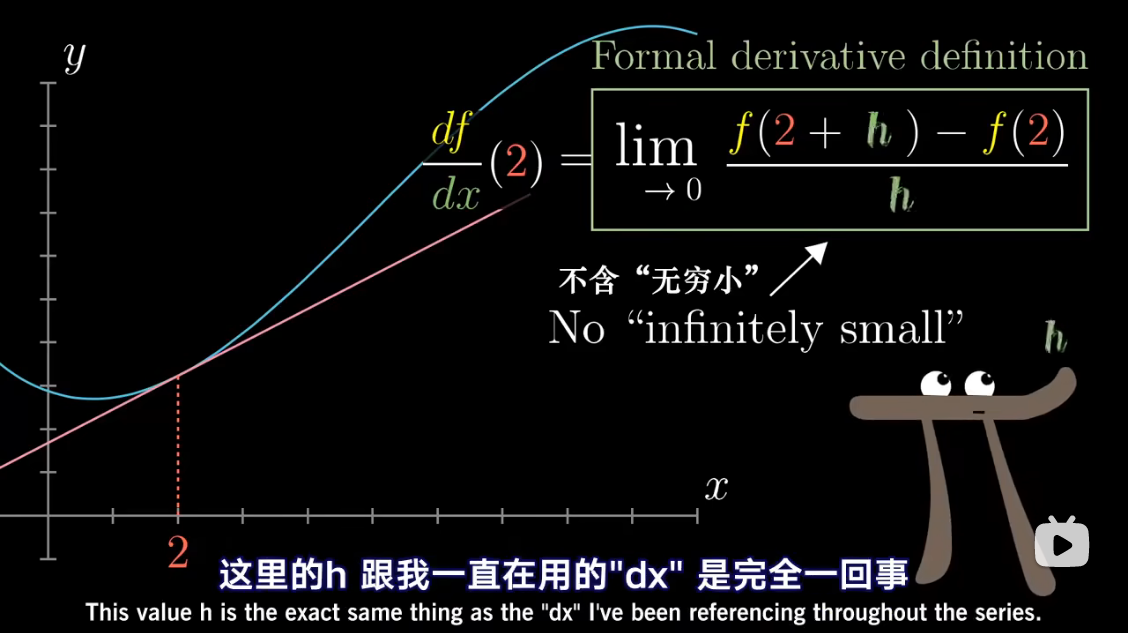
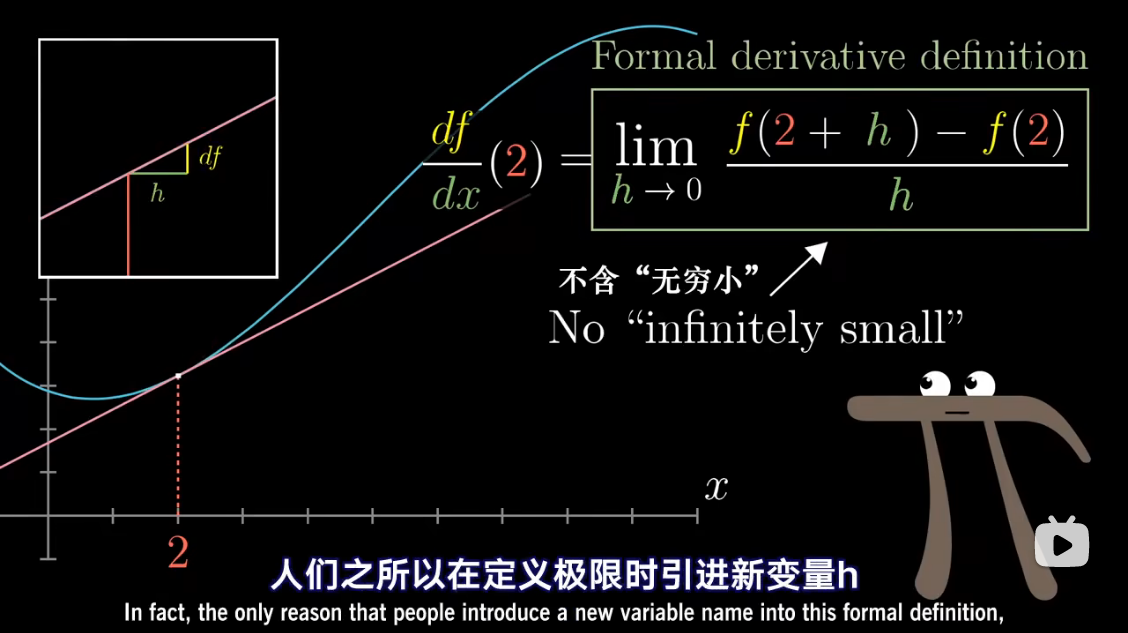










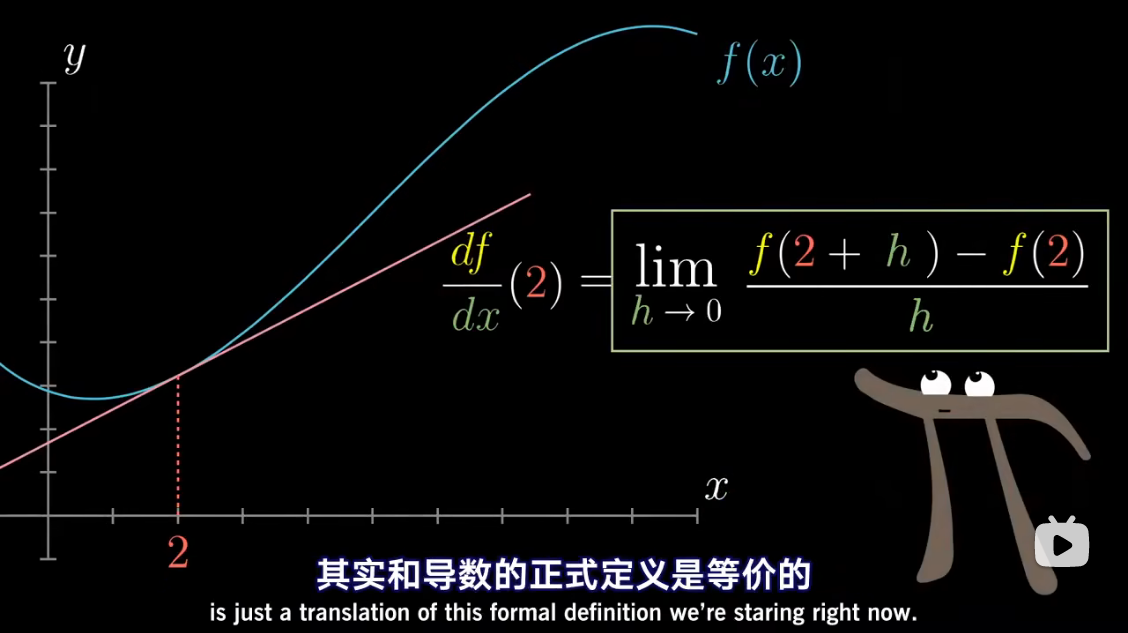
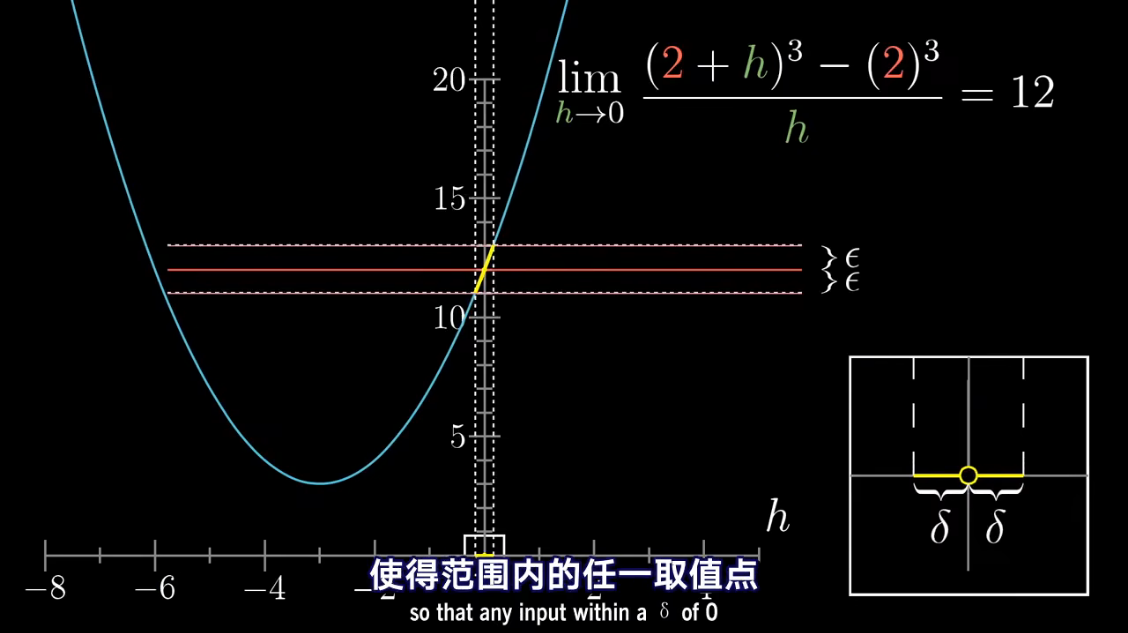
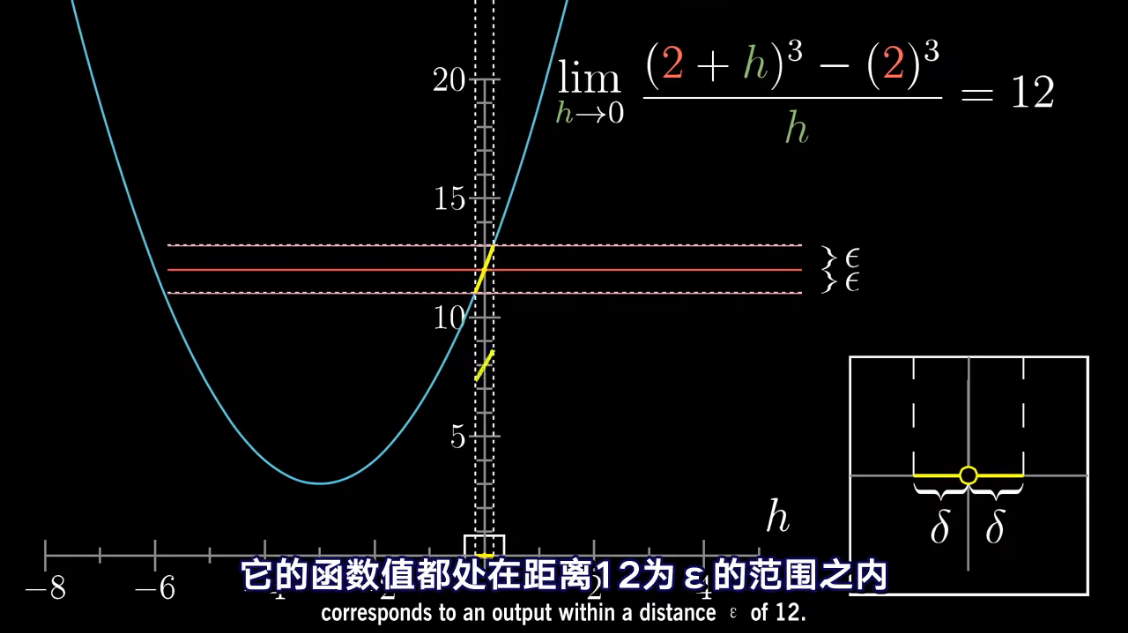
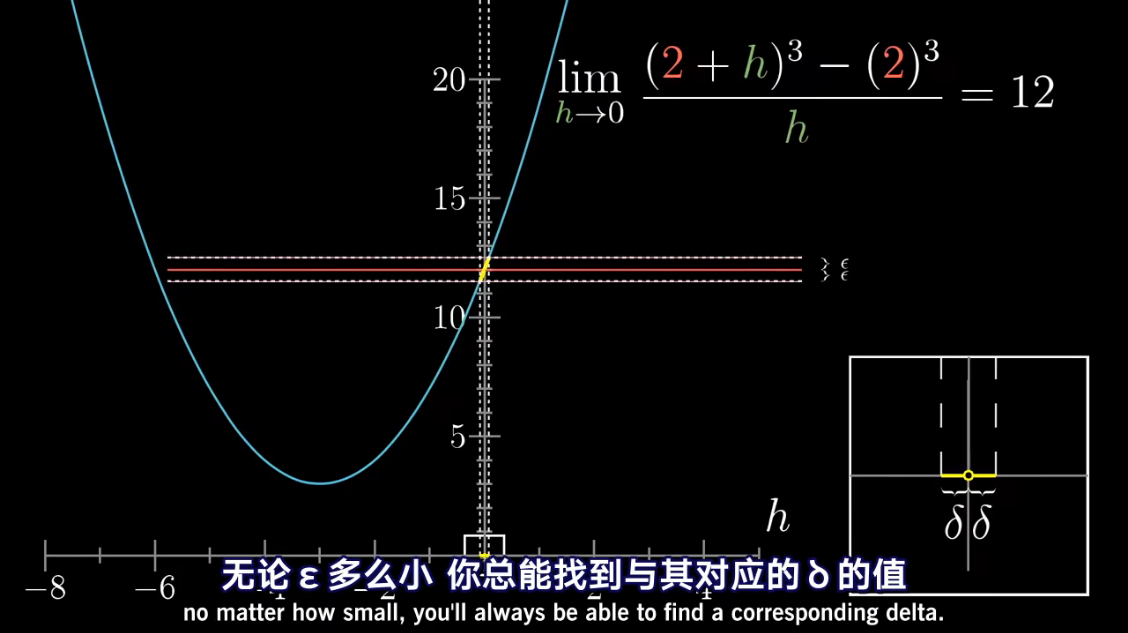
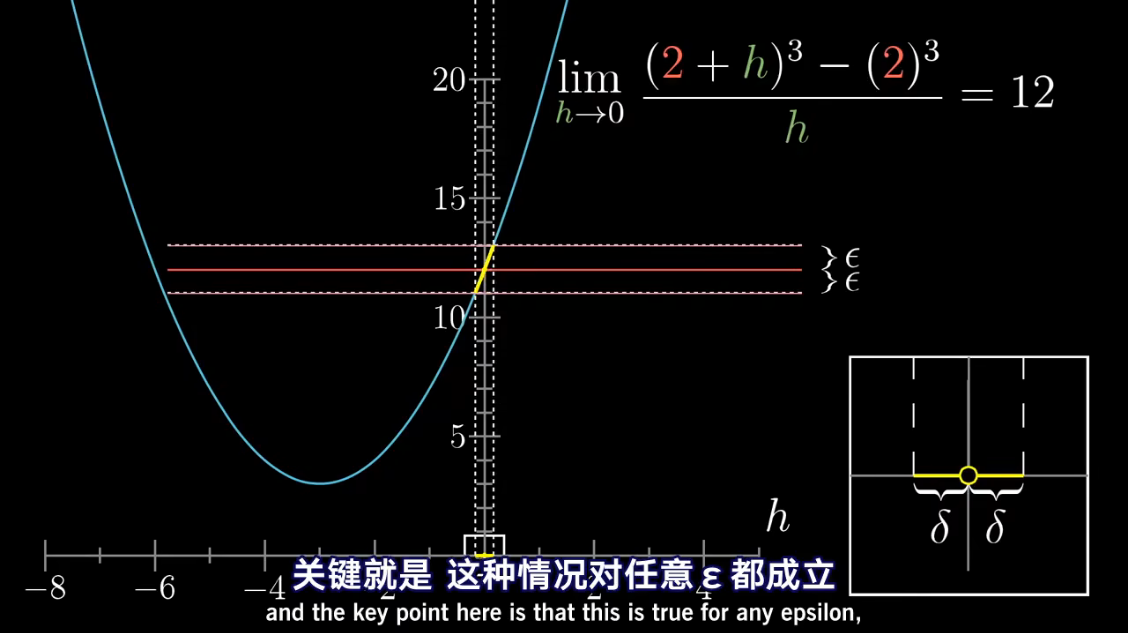
微积分中的 Δ x \Delta x Δx、 Δ y \Delta y Δy 准确含义是什么?能否摒弃它们
_zhihu
个人认为,这两个符号具有误导性,我们时而将 Δ x \Delta x Δx 视为一个整体,时而将其看作变量 x x x 的所谓差分,其准确定义应当是什么?
对于 Δ y \Delta y Δy 也是如此。
微积分引入这两个符号使人困惑后,又用 d x dx dx、 d y dy dy 继续造成混淆,进而有 d y = d f dy = df dy=df 之类的表述,显得十分混乱!
能否完全摒弃 Δ x \Delta x Δx、 Δ y \Delta y Δy,更精确地表达微积分?
提问多天后的个人理解:
看似简单的差分 Δ f \Delta f Δf,最终可定义为与变量 x x x 及步长 h h h 相关的映射,即( Δ f ) ( x ) ( h ) : = f ( x + h ) − f ( x ) (\Delta f)(x)(h) := f(x + h) - f(x) (Δf)(x)(h):=f(x+h)−f(x)
此外,用 ld \text{ld} ld 表示恒同映射,则 Δ x \Delta x Δx 定义为 ld \text{ld} ld 在 x x x 处的差分,步长 h h h 为参变量。
即 Δ x \Delta x Δx 实际上是 ( Δ ld ) ( x ) (\Delta \text{ld})(x) (Δld)(x) 的简写,由于
( Δ ld ) ( x ) ( h ) = ld ( x + h ) − ld ( x ) = h (\Delta \text{ld})(x)(h) = \text{ld}(x + h) - \text{ld}(x) = h (Δld)(x)(h)=ld(x+h)−ld(x)=h,
于是 Δ x ( h ) = h \Delta x(h) = h Δx(h)=h。也就是说, Δ x \Delta x Δx 本质上也是一个恒同映射,只是规定了 x x x 为自变量,因此才有 Δ x = d x \Delta x = dx Δx=dx,因为 d x dx dx 也是一个以 x x x 为自变量的恒同映射。
至于 Δ y \Delta y Δy,理解相对容易,因为 y = f ( x ) y = f(x) y=f(x)。
知乎用户 bewZD3
13 人赞同
研究函数的变化率时,需考虑对自变量赋予一个增量,该增量习惯上记为 Δ x \Delta x Δx,相应地,函数值的变化量习惯上记为 Δ y \Delta y Δy,即 Δ y = f ( x + Δ x ) − f ( x ) \Delta y = f(x + \Delta x) - f(x) Δy=f(x+Δx)−f(x)。
将此增量记为 Δ x \Delta x Δx 是一种习惯,但这种记法对初学者不够友好,易使初学者认为 Δ x \Delta x Δx 与自变量 x x x 存在难以说清的关联,从而产生困惑。实际上,这个增量与 x x x 并无任何关联,而是一个独立的变量,因此目前多数教材会将该增量记为 h h h,以体现其与自变量 x x x 的独立性。
那么 Δ y \Delta y Δy 与 d y dy dy 之间的关系是什么呢? Δ y \Delta y Δy 的定义为 f ( x + h ) − f ( x ) f(x + h) - f(x) f(x+h)−f(x),表示自变量增加 h h h 后函数值的增量。 d y = f ′ ( x ) d x dy = f'(x)dx dy=f′(x)dx,且 Δ y = f ( x + h ) − f ( x ) = d y + o ( h ) = f ′ ( x ) d x + o ( h ) \Delta y = f(x + h) - f(x) = dy + o(h) = f'(x)dx + o(h) Δy=f(x+h)−f(x)=dy+o(h)=f′(x)dx+o(h)。在微积分方法中,用 d y dy dy 代替 Δ y \Delta y Δy 称为线性化,从几何角度而言,体现了微积分“以直代曲”的思想:当自变量的增量较小时, Δ y \Delta y Δy 与 d y dy dy 近似相等;当自变量增量趋向于 0 0 0 时, Δ y \Delta y Δy 与 d y dy dy 可以无限接近,即其极限相等。
匿名用户
4 人赞同
我较支持你的观点,变量和差分均为定义不明确的概念。
在物理中,我们可将变量定义为“时间的函数”,但这在数学中并不恰当,因为时间是典型的物理概念,未必能保留在数学中,数学中真正有意义的是函数。
作为函数,它将一个实数映射为另一个实数,而该实数记为 x x x 还是 y y y 并无实质意义。因此,函数 f f f 的导数记为 f ′ f' f′ 更符合纯分析的视角,但若记为 d y d x \frac{dy}{dx} dxdy,则必须引入物理或几何概念,明确 x x x、 y y y 的具体含义,此时它已不再是单纯的分析学问题。
至于差分,它只能被视为一个整体记号。因为在 Δ x = x 1 − x 2 \Delta x = x_1 - x_2 Δx=x1−x2 这种表述中, x 1 x_1 x1、 x 2 x_2 x2 并未事先定义;即便改为 Δ x = x − x 0 \Delta x = x - x_0 Δx=x−x0,似乎稍好,但仍存在 x 0 x_0 x0 的不确定性,且仍涉及无法通过分析定义的 x x x,未能体现真正的函数性质。
我认为,将 Δ x 0 f ( x ) = f ( x ) − f ( x 0 ) \Delta_{x_0}f(x) = f(x) - f(x_0) Δx0f(x)=f(x)−f(x0) 定义为函数在 x 0 x_0 x0 处的差分是较好的方式,但这仅定义了函数的差分。自变量的差分与自变量的微分,均需引入几何概念,并非单纯的分析学问题。此时, x x x 实际上已是坐标,而非自变量,是点的函数。
最后,不引入差分当然可以纯粹通过极限定义导数,只是表达式会稍显复杂。我们可通过整体记号定义:
D f ( x ) = lim y → 0 f ( x + y ) − f ( x ) y Df(x) = \lim_{y \to 0} \frac{f(x + y) - f(x)}{y} Df(x)=y→0limyf(x+y)−f(x)
这纯粹是一个二元函数的一元极限问题。
此外,还可在多项式中定义 D ∑ k a k x k = ∑ k k a k x k − 1 D\sum_k a_kx^k = \sum_k ka_kx^{k-1} D∑kakxk=∑kkakxk−1,或通过莱布尼兹律进行定义。
RC233
4 人赞同
在物理中, Δ \Delta Δ 符号表示“差值”,例如“若一个物体现在的速度是 10 m/s 10\ \text{m/s} 10 m/s,一分钟前是 5 m/s 5\ \text{m/s} 5 m/s,则 Δ v = 5 m/s \Delta v = 5\ \text{m/s} Δv=5 m/s”,其含义易于理解。
在数学中, Δ \Delta Δ 的含义可结合两点坐标求直线斜率的公式理解:
Y a − Y b X a − X b \frac{Y_a - Y_b}{X_a - X_b} Xa−XbYa−Yb
可见,这里的横纵坐标差值也可表示为 Δ x \Delta x Δx、 Δ y \Delta y Δy。
在微积分中,核心思想是让 Δ x \Delta x Δx、 Δ y \Delta y Δy 趋近于零(即微分),因此这类符号通常被称为微元,其含义与物理中的 Δ \Delta Δ 类似,均表示差值,只是此处为极小的差值。
via:
-
CC | But what is “dx” really? Calculus terms explained
https://blog.cambridgecoaching.com/but-what-is-dx-really-calculus-terms-explained -
calculus - Using d x dx dx for h h h in the definition of derivative - Mathematics Educators Stack Exchange - 2015
https://matheducators.stackexchange.com/questions/9807/using-dx-for-h-in-the-definition-of-derivative -
微积分里面的 Δx、Δy 的准确含义是什么,摒弃它们如何? - 知乎
https://www.zhihu.com/question/323168389






















 3900
3900

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








