Fuzzy Mathematics | Degree of Membership Function

斐夷所非

已于 2025-03-21 23:10:36 修改

阅读量894

点赞数 32

分类专栏： mathematics 文章标签：隶属度函数

于 2025-03-21 11:13:36 首次发布

本文链接：https://blog.youkuaiyun.com/u013669912/article/details/146413768

版权

mathematics 专栏收录该内容

68 篇文章

订阅专栏

注：本文为 “隶属度函数” 相关文章合辑。

略作重排。

如有内容异常，请看原文。

隶属函数（Membership Function），又称归属函数或模糊元函数，是用于表征模糊集合的重要数学工具。在经典集合中，元素与集合的关系只有属于或不属于两种明确情况，分别用 $1$ 和 $0$ 表示。但对于模糊集合而言，元素与集合的隶属关系具有不分明性。

隶属函数正是为描述元素 $u$ 对论域 $U$ 上的一个模糊集合的隶属关系而引入的，它将用区间 $[0, 1]$ 中的数值来代替 $0$ 和 $1$ 这两个值，以此精确地刻画元素属于某模糊集合的 “真实程度”（Degree of Truth）。隶属函数本质上是表征某一元素是否属于某一模糊集合这一模糊概念的数学表达。

隶属度函数

努力学习程序的研究生于 2020 - 09 - 23 10:23:36 发布

隶属度函数

若对论域（研究的范围） $U$ 中的任一元素 $x$ ，都有一个数 $\in [0,1]$ 与之对应，则称 $A$ 为 $U$ 上的模糊集， $A (x)$ 称为 $x$ 对 $A$ 的隶属度。当 $x$ 在 $U$ 中变动时， $A (x)$ 就是一个函数，称为 $A$ 的隶属函数。隶属度 $A (x)$ 越接近于 1，表示 $x$ 属于 $A$ 的程度越高， $A (x)$ 越接近于 0 表示 $x$ 属于 $A$ 的程度越低。用取值于区间 (0,1) 的隶属函数 $A (x)$ 表征 $x$ 属于 $A$ 的程度高低。隶属度属于模糊评价函数里的概念：模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法，其特点是评价结果不是绝对地肯定或否定，而是以一个模糊集合来表示。

隶属度函数的确立还没有一套成熟有效的方法，大多数系统的确立方法还停留在经验和实验的基础上。对于同一个模糊概念，不同的人会建立不完全相同的隶属度函数，尽管形式不完全相同，只要能反映同一模糊概念，在解决和处理实际模糊信息的问题中仍然殊途同归。下面介绍几种常用的方法。

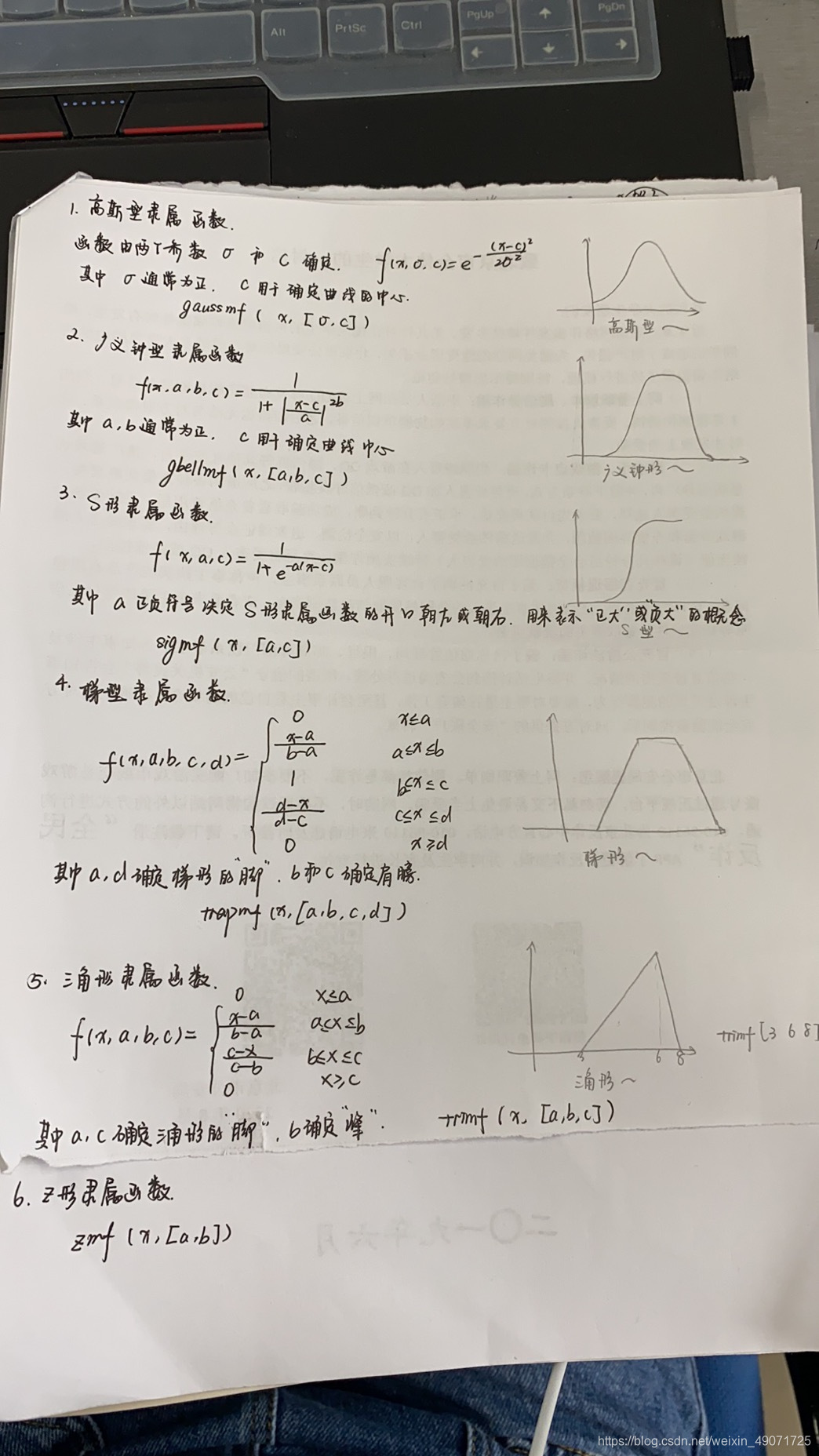
在 MATLAB 中已经开发出了 11 种隶属函数，具体如下表所示：

隶属函数名称	函数类型
双 S 形隶属函数	dsigmf
联合高斯型隶属函数	gauss2mf
高斯型隶属函数	gaussmf
广义钟形隶属函数	gbellmf
II 型隶属函数	pimf
双 S 形乘积隶属函数	psigmf
S 状隶属函数	smf
S 形隶属函数	sigmf
梯形隶属函数	trapmf
三角形隶属函数	trimf
Z 形隶属函数	zmf

在模糊控制中应用较多的隶属函数有以下 6 种。

在这里插入图片描述

模糊数学笔记：模糊隶属度函数的确定及常用隶属度函数

半个冯博士于 2020 - 07 - 15 16:59:32 发布

1、模糊隶属度函数的确定方法

直觉法：人们用自己对模糊概念的认识和理解，或者人们对模糊概念的普遍认同来建立隶属函数。这种方法通常用于描述人们熟知、有共识的客观模糊现象，或者用于难于采集数据的情形。
二元对比排序法：二元对比排序方法就是通过对多个对象进行两两对比来确定某种特征下的顺序，由此来决定这些对象对该特征的隶属程度。这种方法更适用于根据事物的抽象性质由专家来确定隶属函数的情形，可以通过多名专家或者一个委员会，甚至 - - 次民意测验来实施。
模糊统计实验法：类似于统计学中的大样本实验法，根据概念所占比例确定其对应隶属度。

除此之外还有许多其他方法，如最小模糊度法等。

2、常用模糊隶属度函数之基本类型

偏小、偏大和中间型是最为常用的隶属度函数的分类，最为简单常用的是（半）梯形函数：

偏小型：
$\begin{cases} 1, & x < a \\ \frac{b - x}{b - a}, & a \leq x \leq b \\ 0, & b < x \end{cases}$

中间型：
$\begin{cases} \frac{x - a}{b - a}, & a \leq x < b \\ 1, & b \leq x < c \\ \frac{d - x}{d - c}, & c \leq x \leq d \\ 0, & x < a \text{ 或 } d < x \end{cases}$

偏大型：
$\begin{cases} 0, & x < a \\ \frac{x - a}{b - a}, & a \leq x \leq b \\ 1, & b < x \end{cases}$

依次对应下列图形：

在这里插入图片描述

3、抛物型或半抛物型

偏小型：
$\begin{cases} 1, & x < a \\ \left(\frac{b - x}{b - a}\right)^k, & a \leq x \leq b \\ 0, & b < x \end{cases}$

中间型：
$\begin{cases} \left(\frac{x - a}{b - a}\right)^k, & a \leq x < b \\ 1, & b \leq x < c \\ \left(\frac{d - x}{d - c}\right)^k, & c \leq x \leq d \\ 0, & x < a \text{ 或 } d < x \end{cases}$

偏大型：
$\begin{cases} 0, & x < a \\ \left(\frac{x - a}{b - a}\right)^k, & a \leq x \leq b \\ 1, & b < x \end{cases}$

依次对应下列图形：

在这里插入图片描述

其他隶属度函数可参考：

Membership functions

隶属度函数模板

闪闪亮亮于 2017 - 08 - 21 21:19:19 发布

模糊隶属度函数划分等级

根据国家对信号交叉路口的评价标准，对交通状况分为 4 个等级，分别为 Ⅰ 级舒适畅通、Ⅱ 级接近饱和、Ⅲ 级常呈混乱、Ⅳ 级阻塞。因此选用 4 个等级的模糊隶属度函数。分别为：

某时段交通状况对 Ⅰ 级路况的隶属度函数：

$u(\eta)= \begin{cases} 1, & \eta \leq a \\ \frac{b - \eta}{b - a}, & a \leq \eta \leq b \\ 0, & \eta \geq b \end{cases}$

某时段交通状况对 Ⅱ 级路况的隶属度函数：

$u(\eta)= \begin{cases} 0, & \eta \leq a,\eta \geq c \\ \frac{\eta - a}{b - a}, & a \leq \eta \leq b \\ \frac{c - \eta}{c - b}, & b \leq \eta \leq c \end{cases}$

某时段交通状况对 Ⅲ 级路况的隶属度函数：

$u(\eta)= \begin{cases} 0, & \eta \leq b,\eta \geq d \\ \frac{\eta - b}{c - b}, & b \leq \eta \leq c \\ \frac{d - \eta}{d - c}, & c \leq \eta \leq d \end{cases}$

某时段交通状况对 Ⅳ 级路况的隶属度函数：

$u(\eta)= \begin{cases} 0, & \eta \leq c \\ \frac{\eta - c}{d - c}, & c \leq \eta \leq d \\ 1, & \eta \geq d \end{cases}$

式中：(\eta) 为交通状况指数计算值；(a,b,c,d) 分别对应该交通路况指数对应 Ⅰ 级、Ⅱ 级、Ⅲ 级和 Ⅳ 级道路状况的标准值，这里分别取 0.2、0.4、0.6、0.8。相应的隶属度函数图像如下：

图 5 隶属度函数分级示意图

将表 6 中的数据带入模糊隶属度函数中，得到交通状况指数 i 对级别 j 的隶属度矩阵见附录，根据最大隶属度原则，将各个时间段各个行进方式的道路交通情况划分等级如下表：

表 7 交叉口道路交通等级时空分布

	掉头	西直	南左	东直	东左
0~5min	Ⅱ	Ⅰ	Ⅳ	Ⅱ	Ⅲ
5~10min	Ⅰ	Ⅱ	Ⅲ/Ⅳ	Ⅰ	Ⅲ
10~15min	Ⅰ	Ⅰ	Ⅳ	Ⅰ	Ⅱ
15~20min	Ⅰ	Ⅱ	Ⅳ	Ⅰ	Ⅲ
20~25min	Ⅰ	Ⅰ	Ⅳ	Ⅰ	Ⅲ
平均状况	Ⅰ	Ⅰ	Ⅳ	Ⅰ	Ⅲ

Ⅰ 级舒适畅通、Ⅱ 级接近饱和、Ⅲ 级常呈混乱、Ⅳ 级阻塞）
画出相应的等级变化图

图 6 交通等级变化图

结论

西进口掉头、西进口直行、南进口左转、东进口直行、东进口左转这 5 个方向的平均交通状况等级分别为 Ⅰ 级、Ⅰ 级、Ⅳ 级、Ⅰ 级和 Ⅲ 级。
交通状况最好的有西进口掉头、西进口直行、东进口直行三个行进方向，均为 Ⅰ 级舒适畅通。
交通状况最差是南进口左转行进方向，为 Ⅳ 级阻塞。
某行进方向上在该时段的交通状况等级是稳定的，不会发生大的变化，如上图中西进口直行方向仅在 Ⅰ 级、Ⅱ 级波动。

对应的代码：

function lishu = f(x)
    a = 0.2; b = 0.4; c = 0.6; d = 0.8;
    % 第一级程度
    if x <= a
        lishu(1) = 1;
    elseif x >= a && x <= b
        lishu(1) = (b - x) / (b - a);
    else
        lishu(1) = 0;
    end

    % 第二级程度
    if x <= a || x >= c
        lishu(2) = 0;
    elseif x >= a && x <= b
        lishu(2) = (x - a) / (b - a);
    elseif x >= b && x <= c
        lishu(2) = (c - x) / (c - b);
    end

    % 第三级程度
    if x <= b || x >= d
        lishu(3) = 0;
    elseif x >= b && x <= c
        lishu(3) = (x - b) / (c - b);
    elseif x >= c && x <= d
        lishu(3) = (d - x) / (d - c);
    end

    % 第四级程度
    if x <= c
        lishu(4) = 0;
    elseif x >= c && x <= d
        lishu(4) = (x - c) / (d - c);
    else
        lishu(4) = 1;
    end
end

模糊数学（一）：模糊集及其表示

Evanism_小风铃于 2020-06-29 09:36:02 发布

1. 模糊集合特点

模糊集合用来表达模糊性概念的集合，承认亦此亦彼。
经典集合强调非此即彼。

2. 模糊集合的隶属函数

隶属函数

其中模糊集合 $A$ 是由隶属函数唯一确定的，所以模糊集合与隶属函数可以看作是等同的。

3. 模糊集合的表示

模糊集合表示

扎德表示法： $A(X_i)$ 只是表示对于 $X_i$ 的隶属度，而不是代数意义上的相加。
序偶表示法：每个 $X_i$ 都对应其隶属度。
向量表示法：在序偶表示法的基础上，省略了对于 $X_i$ 的表达。

无穷相加表示

基于扎德表示法，无穷上的相加常用微分表示。

4. 模糊集合的表达实例

论域为有限集时

有限集表示

论域为无限集时

无限集表示

模糊数学（二）：隶属函数的确定

Evanism_小风铃于 2020-06-29 10:02:58 发布

确定隶属函数常用的方法有以下三种：

模糊统计法
指派法
借用已有的客观尺度

1. 模糊统计法

模糊统计法更偏向于概率的方法，通过统计与计算概率使得隶属频率趋于稳定。

2. 指派法

指派法通过已有的函数模型，将自己的实例放入对应的函数模型中完成隶属函数的确定。

指派法

偏大型的 $f (x)$ 常常为增函数，而偏小型的为减函数。

以下是常见的函数模型：

函数模型1

函数模型2

函数模型3

例题：试确定 $A =$ “年轻人” 的隶属函数。
当年龄的取值越大时，其越不属于 $A$ 集合，则我们采取选用减函数的数学模型，如选择偏小型柯西分布。

偏小型柯西分布

假定我们将 20 岁作为年轻人的分界线，则 $a = 20$ 。
$\beta$ 常取值为 2，因为平方项会忽视正负而求得差值。
$\alpha$ 常常用于调整函数，若我们将 30 岁的隶属值设定为 0.5，则将 $A (30) = 0.5$ 带入，求得 $\alpha = \frac{1}{25}$ 。